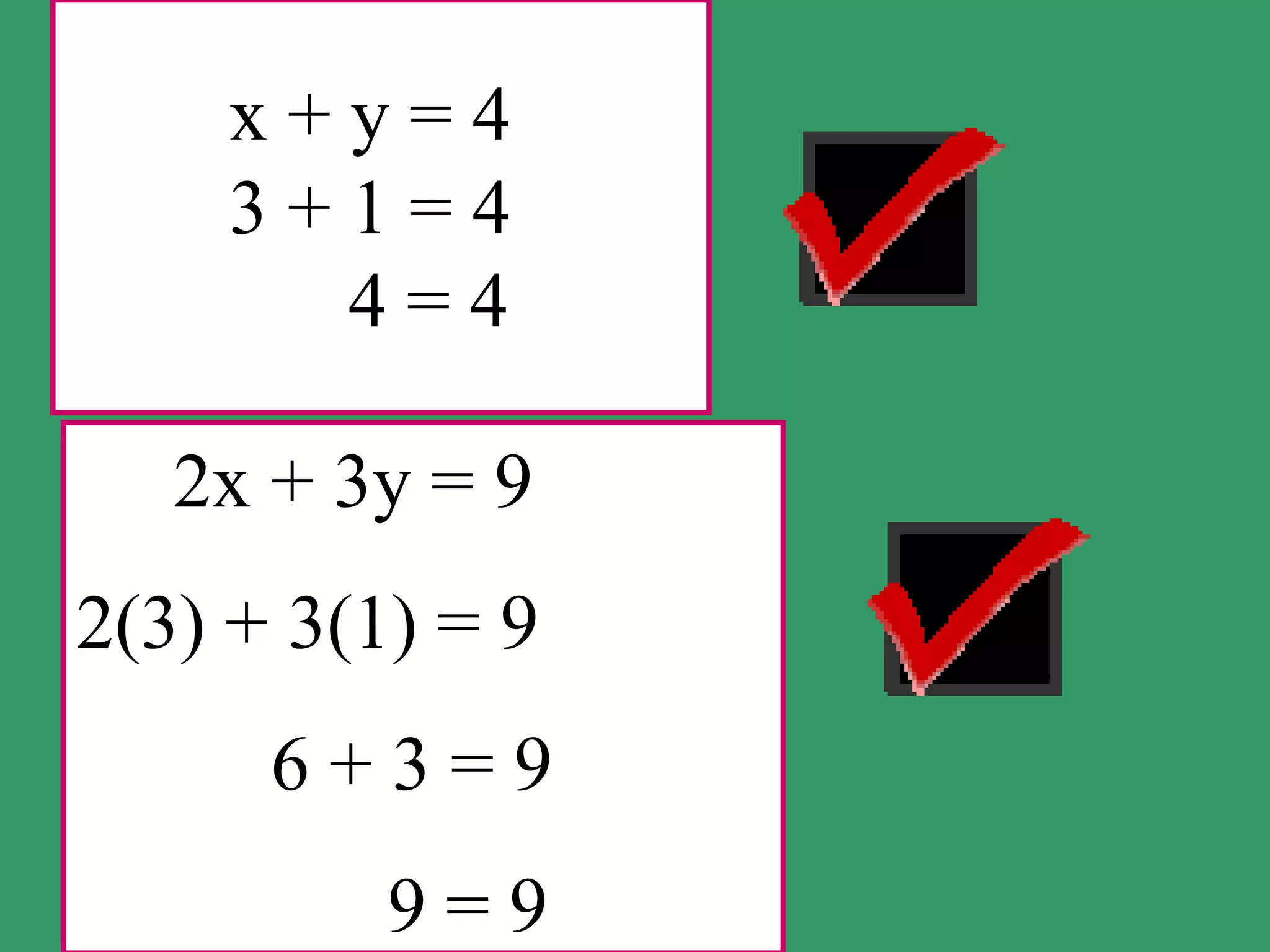This document provides instructions for solving systems of equations using elimination. It demonstrates eliminating variables by adding or subtracting equations. Sample systems are worked through, showing the steps of identifying which variable to eliminate, combining the equations accordingly, solving for one variable, then substituting back into the original equations to solve for the other. The solutions are checked in both equations to verify they satisfy the system.

2. BY GRAPHING
Y = 2X + 1
Y = -X + 4
(1,3) IS THE
SOLUTION

3. Graphing is not the only way to
solve a system of equations. It is
not really the best way because it
has to be graphed perfectly and
some answers are not integers.
SOOOO
We need to learn another way!!!!

4. Solve:
by ELIMINATION
x + y = 12
-x + 3y = -8
We need to
eliminate
(get rid of)
a variable.
The x’s will
be the
easiest. So,
we will add
the two
equations.
4y = 4 Divide by 4
y = 1
THEN----
Like variables
must be lined
under each
other.

5. X +Y = 12
(11,1)
Substitute
your answer
into either
original
equation and
solve for the
second
variable.
Answer
Now check our answers
in both equations------
x + 1 = 12
-1 -1
x = 11

6. X + Y =12
11 + 1 = 12
12 = 12
-x + 3y = -8
-11 + 3(1) = -8
-11 + 3 = -8
-8 = -8

7. Solve:
by ELIMINATION
5x - 4y = -21
-2x + 4y = 18
We need to
eliminate
(get rid of)
a variable.
The y’s be
will the
easiest.So,
we will add
the two
equations.
3x = -3 Divide by 3
x = -1
THEN----
Like variables
must be lined
under each
other.

8. 5X - 4Y = -21
(-1, 4)
Substitute
your answer
into either
original
equation and
solve for the
second
variable.
Answer
Now check our answers
in both equations------
5(-1) – 4y = -21
-5 – 4y = -21
5 5
-4y = -16
y = 4

9. 5x - 4y = -21
5(-1) – 4(4) = -21
-5 - 16 = -21
-21 = -21
-2x + 4y = 18
-2(-1) + 4(4) = 18
2 + 16 = 18

10. Solve:
by ELIMINATION
2x + 7y = 31
5x - 7y = - 45
We need to
eliminate
(get rid of)
a variable.
The y’s will
be the
easiest. So,
we will add
the two
equations.
7x = -14 Divide by 7
x = -2
THEN----
Like variables
must be lined
under each
other.

11. 2X + 7Y = 31
(-2, 5)
Substitute
your answer
into either
original
equation and
solve for the
second
variable.
Answer
Now check our answers
in both equations------
2(-2) + 7y = 31
-4 + 7y = 31
4 4
7y = 35
y = 5

12. 2x + 7y = 31
2(-2) + 7(5) = 31
-4 + 35 = 31
31 = 31
5x – 7y = - 45
5(-2) - 7(5) = - 45
-10 - 35 = - 45
- 45 =- 45

13. Solve:
by ELIMINATION
x + y = 30
x + 7y = 6
We need to eliminate
(get rid of) a variable.
To simply add this
time will not eliminate
a variable. If one of the
x’s was negative, it
would be eliminated
when we add. So we
will multiply one
equation by a – 1.
Like variables
must be lined
under each
other.

14. X + Y = 30
X + 7Y = 6( ) -1
X + Y = 30
-X – 7Y = - 6
Now add the two
equations and
solve.
-6Y = 24
- 6 - 6
Y = - 4
THEN----

15. X + Y = 30
(34, - 4)
Substitute
your answer
into either
original
equation and
solve for the
second
variable.
Answer
Now check our answers
in both equations------
X + - 4 = 30
4 4
X = 34

16. x + y = 30
34 + - 4 = 30
30 = 30
x + 7y = 6
34 + 7(- 4) = 6
34 - 28 = 6
6 = 6

17. Solve:
by ELIMINATION
x + y = 4
2x + 3y = 9
We need to eliminate
(get rid of) a variable.
To simply add this
time will not eliminate
a variable. If there was
a –2x in the 1st
equation, the x’s would
be eliminated when we
add. So we will
multiply the 1st
equation by a – 2.
Like variables
must be lined
under each
other.

18. X + Y = 4
2X + 3Y = 9
-2X - 2 Y = - 8
2X + 3Y = 9
Now add the two
equations and
solve.
Y = 1
THEN----
( ) -2

19. (3,1)
Substitute
your answer
into either
original
equation and
solve for the
second
variable.
Answer
Now check our answers
in both equations------
X + Y = 4
X + 1 = 4
- 1 -1
X = 3

20. x + y = 4
3 + 1 = 4
4 = 4
2x + 3y = 9
2(3) + 3(1) = 9
6 + 3 = 9
9 = 9