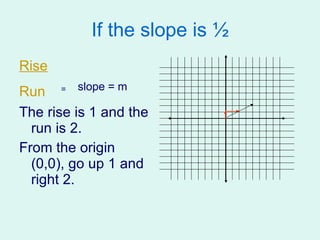
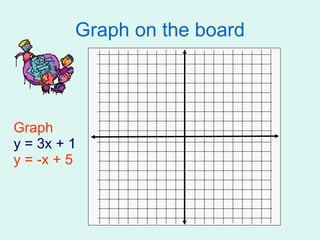
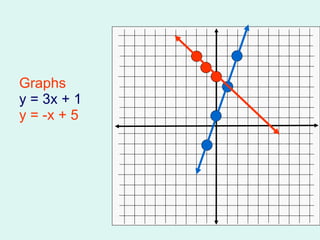
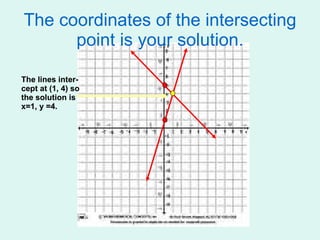
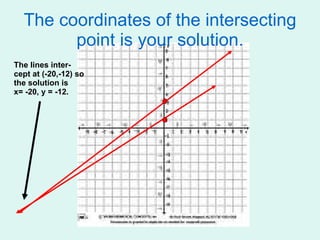
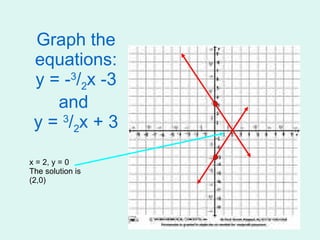
This document introduces different methods for solving systems of linear equations: graphing, substitution, and elimination. It provides examples of solving systems by graphing them on a coordinate plane and finding the point of intersection. It also gives examples of converting equations between standard and slope-intercept form and using substitution and elimination to solve systems algebraically.

1. Solving Linear Equations Using Graphing Substitution and Elimination Introduction to Unit Six

2. What’s the Deal? There are a number of ways to solve groups of linear equations. In this lesson, we will find points on a coordinate plane that solve linear equations in standard form and y-intercept form.

3. Three Parts (over the next few days) Part One – Solve linear equations by graphing. Part Two – Solve linear equations by substitution. Part Three – Solve linear equations by elimination.

4. Solving for linear equations answers the question: What values of x and y fit into both equations? The answer is usually given in (x,y) format (ie. (-4, 6) or (3,8).

5. Remember - Slope intercept form: y = mx + b m = slope b = y-intercept In y = 1/2x – 7 , What is the y-intercept? What is the slope? Rise over Run Rise = up, or plus one (+1) Run = right, or plus two (+2).

6. If the slope is ½ Rise Run = slope = m The rise is 1 and the run is 2. From the origin (0,0), go up 1 and right 2.

7. Graphing Systems of equations y = 3x + 1 y = -x + 5 Since both are in y-intercept format (y=mx+b) find the point through which the line intercepts the y-axis. Graph these equations. Answers on the next slides.

8. Graph on the board Graph y = 3x + 1 y = -x + 5

9. Graphs y = 3x + 1 y = -x + 5

10. Solving By Graphing Which point or points can fit into both equations? The result is the ( x,y ) coordinates of the intersection.

11. The coordinates of the intersecting point is your solution. The lines inter- cept at (1, 4) so the solution is x=1, y =4. The lines inter- cept at (1, 4) so the solution is x=1, y =4.

12. Solve by graphing y = x +3 y = x +1 The next two slides will show the solution.

13. The coordinates of the intersecting point is your solution. The lines inter- cept at (-20,-12) so the solution is x= -20, y = -12.

14. Now solve equations in standard form. 3 x + 2y = -6 and -3 x + 2y = 6 Step One: Convert equations from standard form to y-intercept form. Let’s review that from a previous lesson using the equations above…

15. Change 3x + 2y = -6 to y-intercept form 3x + 2y = -6 - 3x -3x -2y = -3x - 6 Now we need to get y isolated. In this case, let’s divide both sides by 2. 2y = -3x - 6 2 2 2 Now simplify. y = - x -3 Subtract -3x from both sides

16. Change -3x + 2y = 6 to y-intercept form -3x + 2y = +6 + 3x 3x 2y = 3x + 6 Get y isolated. Divide both sides by 2. 2y = 3x + 6 2 2 2 Now simplify. y = 3 / 2 x + 3 Add 3x to both sides

17. Graph the equations: y = - 3 / 2 x -3 and y = 3 / 2 x + 3 x = 2, y = 0 The solution is (2,0)

18. Math is NOT a Spectator Sport Write it Out!

19. End of Part One Assignment: pg. 323-4: 10 - 27

20. Extras for presentation x y -4 -2 0 +2 +4 -6 -4 -2 0 +2 +4 +6