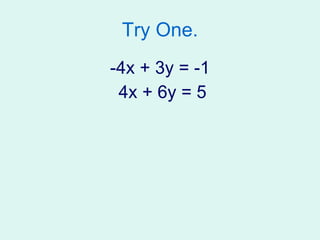This document discusses solving systems of linear equations by elimination. It provides examples of eliminating variables with opposite coefficients as well as multiplying equations to create opposite coefficients. The key steps are to multiply one equation by a number to create opposite coefficients, add or subtract the equations to eliminate one variable, then solve for the remaining variable and back substitute to solve for the other. Elimination avoids lengthy substitution and allows direct solving of systems of equations.

1. Part Three – Solving equations by Elimination Holt Algebra I Text pages 330-334

2. Solve using substitution after manipulating equations in standard form. 2x + 3y = 21 -3x – 3y = -12 Which value, x or y, should we work with first? This looks like a very long, drawn-out problem. Is there a better way?

3. Let’s solve by elimination. This method uses opposites to eliminate one of the variables. Which variable should be eliminated? 2x + 3y = 21 -3x – 3y = -12

4. 2x + 3y = 21 -3x – 3y = -12 Notice that the coefficients with the y value are opposites. (+3 and -3). Use Columns Solve for remaining variable. Substitute that value. If we combine these two equations together in columns, we can eliminate the y values. We will solve for x and then insert it’s value into one of the original equations to solve for y.

5. The steps and explanations 2x + 3y = 21 -3x – 3y = -12 -1x + 0 = 9 -1x + 0= 9 -1 -1 x = -9 Add terms from top to bottom. +2x - 3x +3y - 3y Divide both sides by -1 . Now go back and insert -9 for x.

6. 2x + 3y = 21 -3x – 3y = -12 You may insert (x= -9) into either one. 2(-9) + 3y = 21 -18 + 3y = 21 (add 18 to both sides) +3y = 39 3 3 y = 13 Solution (-9, 13) -3(-9) – 3y = -12 +27 – 3y = -12 (subtract 27 from both sides) -3y = -39 -3 -3 y = 13

7. Try One. -4x + 3y = -1 4x + 6y = 5

8. Eliminate the x values. -4x + 3y = -1 4x + 6y = 5 9y = 4 9y = 4 9 9 y = 4 / 9 Solve for x. 4x + 6( 4 / 9 ) = 5 4x + 24 / 9 = 45 / 9 Subtract 21 / 9 from both sides. 4x = 2 1 / 3 Go to the next slide…

9. 4x = 21 / 9 Divide both sided by 4. 4x = 21 / 9 4 4 x = x = To divide fractions, multiply by the reciprocal

10. Ready to go one more step? What if you don’t have an easy choice. You may find that neither equation has opposite coefficients. 11x + 2y = -8 8x + 3y = 5

11. Let’s try 11x + 2y = -8 and 8x + 3y = 5 Goal Observe Multiply eliminate a variable using opposite coefficients. It looks like we should use 2y and 3y since they are smaller numbers both sides of the top equation by -3 and both sides of the bottom by 2, we should get coefficients of 6 and -6.

12. Multiply both sides (11x + 2y) = (-8) (8x + 3y) = (5) -3(11x + 2y) = (-8)-3 2(8x + 3y) = (5)2 We’ll put all four values into parentheses. Multiply both sides of the top by -3 Multiply both sides of the second equation by 2.

13. Results of the First Steps -3(11x + 2y) = (-8)-3 2(8x + 3y) = (5)2 ----------------------- -33x – 6y = +24 16x + 6y = +10 -17x + 0 = 34 From the previous slide Use the distributive property Now eliminate

14. From previous slide -17x = 34 x = -2 11x + 2y = -8 11(-2) + 2y = -8 -22+ 2y = -8 2y = 14 y = 7 Pick one of the original equations. Solve for the other variable. Add 22 to both sides. -8 +22 = 14. Solution (-2, 7)

15. One more for practice 3x - 2y = 2 4x – 7y = 33 -------------------- -4(3x - 2y) = (2)-4 3(4x – 7y) = (33)3 ------------------------- Solution on the next slide…

16. One more for practice - Solution 3x - 2y = 2 4x – 7y = 33 -------------------- -4(3x - 2y) = (2)-4 3(4x – 7y) = (33)3 ------------------------- -12x + 8y = -8 12x – 21y = 99 ----------------------- -13y = 91 -13y = 91 -13 -13 y= -7 --------------------------- 3x-2(-7)= 2 3x + 14 = 2 3x = -12 x= -4 ------------- Solution (-4, -7)

17. Which way of solving works best for you? Graphing? Substitution? Elimination? Make sure you know them all in order to pick the best way to solve each problem.

18. Assignment: 334:15-33 & 41-47 odds