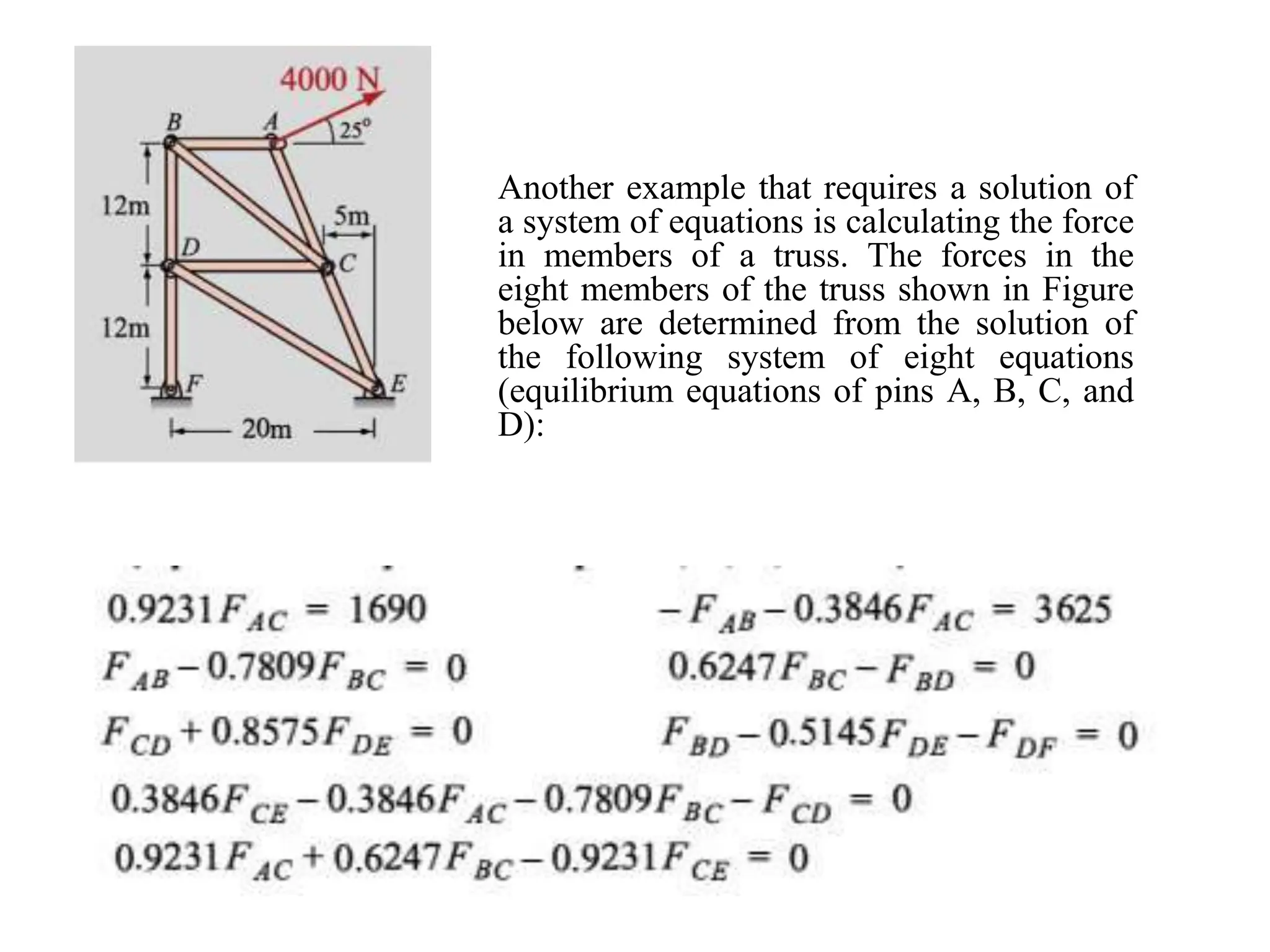
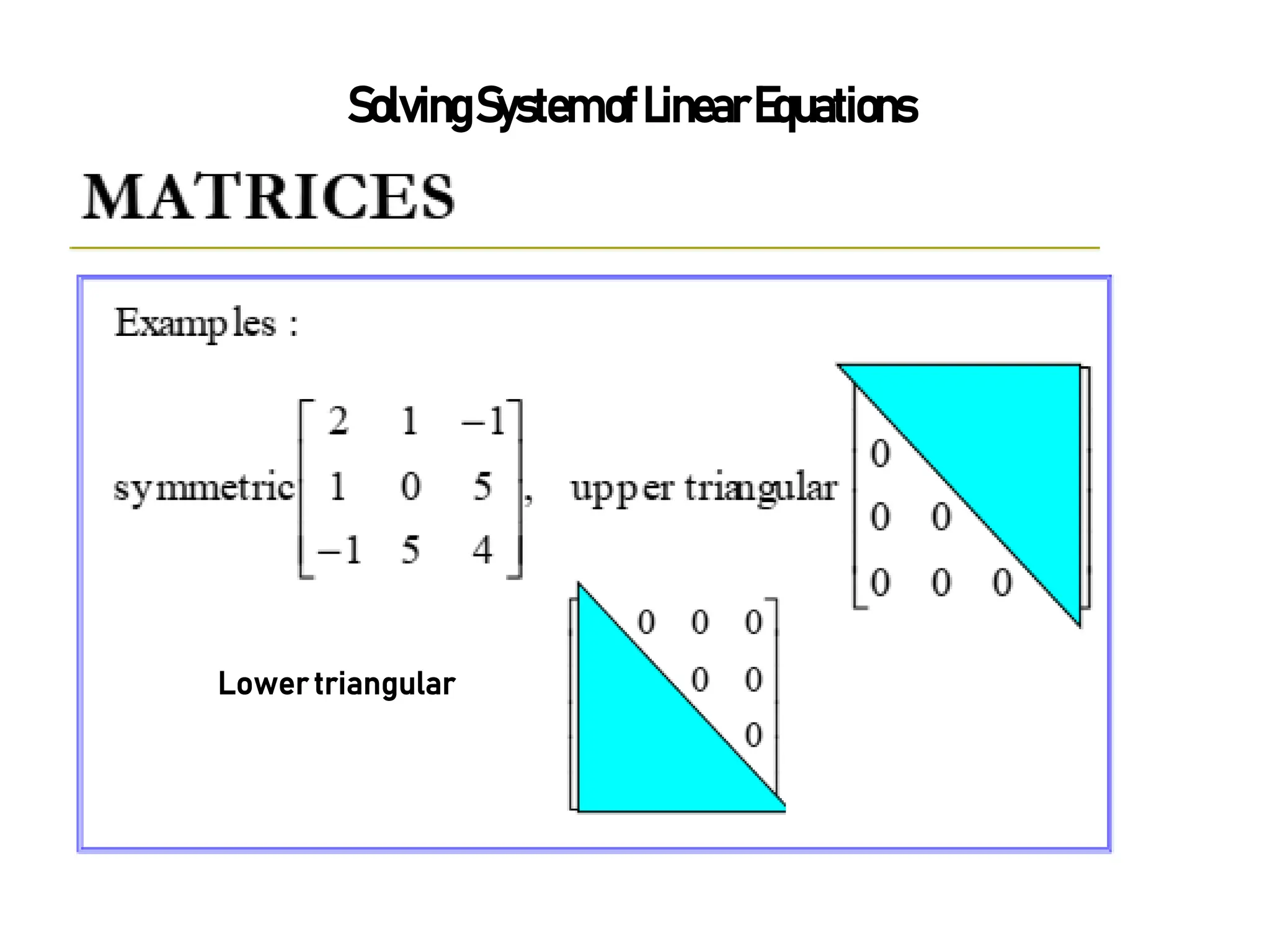
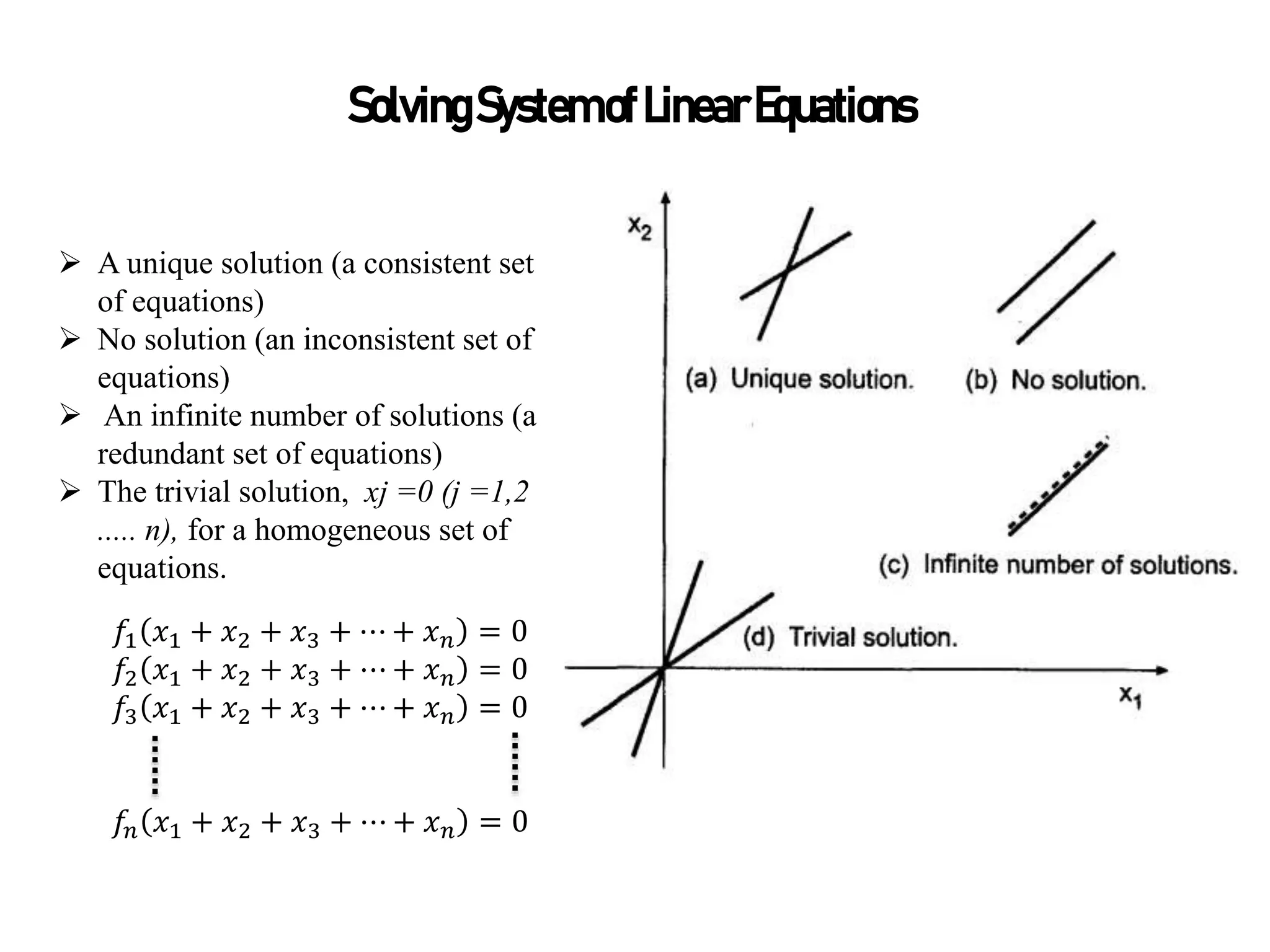
The document discusses systems of linear equations and methods for solving them. It defines a system of linear equations as multiple linear equations with the same number of unknown variables. Systems can be written in matrix form and solved using methods like Cramer's Rule, matrix inverse, graphical analysis, substitution, and numerical methods for systems with more than 3 equations like Gauss-Siedel, Jacobi, Gauss elimination, Gauss-Jordan, and LU decomposition. Systems can have a unique solution, no solution, an infinite number of solutions, or the trivial solution where all variables equal 0. Systems are used in areas like electrical circuit analysis and force analysis in trusses.

1. Chapter 3
Solving System of Linear
Equations

2.  A system of linear Equations is composed of linear
equations that are aimed at expressing a physical system or
process using linear relationship .
 An n- number of equation with n- number of unknowns is
written
𝑓1 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
𝑓2 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
𝑓3 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
𝑓𝑛 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
SolvingSystemofLinearEquations

3.  A linear equation has a general form of
f(x) = a x + b = 0
 An n - number of linear equation with n- number of
unknowns is written in general form
𝑎11𝑥1 + 𝑎12𝑥2 + 𝑎13𝑥3 + ⋯ + 𝑎1𝑛𝑥𝑛 = 𝑏1
𝑎21𝑥1 + 𝑎22𝑥2 + 𝑎23𝑥3 + ⋯ + 𝑎2𝑛𝑥𝑛 = 𝑏2
𝑎31𝑥1 + 𝑎32𝑥2 + 𝑎33𝑥3 + ⋯ + 𝑎3𝑛𝑥𝑛 = 𝑏3
𝑎𝑛1𝑥1 + 𝑎𝑛2𝑥2 + 𝑎𝑛3𝑥3 + ⋯ + 𝑎𝑛𝑛𝑥𝑛 = 𝑏𝑛
SolvingSystemofLinearEquations

4. An n- number of linear equation with n-
number of unknowns is written in matrix form
𝑎11 ⋯ 𝑎1𝑛
⋮ ⋱ ⋮
𝑎𝑛1 ⋯ 𝑎𝑛𝑛
𝑥1
⋮
𝑥𝑛
=
𝑏1
⋮
𝑏𝑛
SolvingSystemofLinearEquations

5. SolvingSystemofLinearEquations
 A system of linear equations
can be used in electrical circuit
analysis, Force analysis in truss,
finite element, finite difference
and also other areas including
non engineering disciplines as
well.

6. Another example that requires a solution of
a system of equations is calculating the force
in members of a truss. The forces in the
eight members of the truss shown in Figure
below are determined from the solution of
the following system of eight equations
(equilibrium equations of pins A, B, C, and
D):

7. 0 0.9231 0
1
0
0
0
−1
0
0
0
0
−0.3846
0.9231
−0.3846
0
0
−0.7809
0
−0.7809
0.6247
0
0.6247
0
0 0 0
0
0
0
0
0
−1
1
0
0
0
0
0
0
0
0
0
0.3846
−0.9231
0
0
0
0
0
0.8575
0
0
0
0
−0.5145
0
0
0
0
0
0
0
−1
𝐹𝐴𝐵
𝐹𝐴𝐶
𝐹𝐵𝐶
𝐹𝐵𝐷
𝐹𝐶𝐷
𝐹𝐶𝐸
𝐹𝐷𝐸
𝐹𝐷𝐹
=
1690
0
0
0
0
3625
0
0
It can be written
in Matrix Form

8. SolvingSystemofLinearEquations

9. SolvingSystemofLinearEquations

10. SolvingSystemofLinearEquations
Lower triangular

11. SolvingSystemofLinearEquations
det(a) = (𝒂𝒊𝒋∗ −𝟏
𝒊 + 𝒋
∗ 𝑴𝒊𝒏𝒐𝒓𝒊𝒋)

12. SolvingSystemofLinearEquations

13. SolvingSystemofLinearEquations
 A unique solution (a consistent set
of equations)
 No solution (an inconsistent set of
equations)
 An infinite number of solutions (a
redundant set of equations)
 The trivial solution, xj =0 (j =1,2
..... n), for a homogeneous set of
equations.
𝑓1 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
𝑓2 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
𝑓3 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0
𝑓𝑛 𝑥1 + 𝑥2 + 𝑥3 + ⋯ + 𝑥𝑛 = 0

14. SolvingSystemofLinearEquations
Cramer’s Rule
Consider the system of linear algebraic equations,
Ax= b, which represents n equations. Cramer’s rule states
that the solution for
Where Aj is the n x n matrix obtained by replacing column j
in matrix A by the column vector b.
For example, consider the system of two linear algebraic
equations

15. SolvingSystemofLinearEquations
Matrix Inverse Method
Systems of linear algebraic equations can be solved using the matrix
inverse,A -1 . Consider the general system of linear algebraicequations:
Multiplying by
Not all matrices have inverses. Singular matrices, that is, matrices
whose determinantis zero, do not have inverses.The corresponding
system of equations does not have a unique solution.

16. SolvingSystemofLinearEquations
 Whenever the number of equation in the system of equations
become greater than 3, the methods like Cramer’s, inverse,
graphical and substitution becomes complex and time
consuming. So in order to avoid such difficulties numerical
methods are proposed.
 Numerical methods used to solve a system of Linear equations
are classified in to 2.
1. Iterative(Indirect) Methods
1. Gauss Siedel Method
2. Jacobi Method
2. Direct Method
1. Gauss Elimination Method
2. Gauss Jordan Method
3. LU Decomposition Method