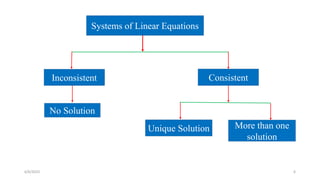
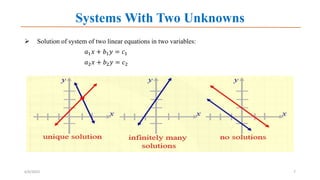
The document provides information about Shahina Akter and her background in mathematics. It then outlines topics in linear algebra including systems of linear equations, matrix algebra, and objectives. It introduces concepts such as the augmented matrix, row echelon form, homogeneous systems, and solving systems using Gaussian elimination and back substitution. The document offers examples and step-by-step explanations of solving systems with unique solutions, no solutions, and infinite solutions.

1. Shahina Akter
Ph.D. Fellow & M.S in Applied Mathematics, DU
B.Sc in Mathematics, DU

2. Linear Algebra
Systems of Linear Equations
• Introduction to Systems of Linear Equations
• Gaussian Elimination and Gauss-Jordan Elimination
• Applications of Systems of Linear Equations
Matrix Algebra
• Matrices and Matrix Operations
• Linear systems and Invertible Matrices
6/6/2023 2

3. Objectives
 Recognize, graph, and solve a system of linear equations in n unknowns.
 Use back substitution to solve a system of linear equations.
 Determine whether a system is consistent or inconsistent.
 Determine if a matrix is in row-echelon form or reduced row-echelon form.
 Use element row operations with back substitution to solve a system in row-echelon form.
 Use elimination to rewrite a system in row-echelon form.
 Write an augmented or coefficient matrix from a system of linear equations, or translate a
matrix into a system of linear equations.
 Solve a system of linear equations using Gaussian Elimination.
 Solve a homogeneous system of linear equations.
6/6/2023 3

4. Introduction
An equation in two or more variables is linear if it contains no products or powers of the variables.
Linear Equations in two variables: 𝑎𝑥 + 𝑏𝑦 = 𝑐
Linear Equations in n variables: 𝑎1𝑥1 + 𝑎2𝑥2 + ⋯ + 𝑎𝑛𝑥𝑛 = 𝑏
• Coefficients: 𝑎1, 𝑎2, … 𝑎𝑛 ⟹ real number
• Constant term: b ⟹ real number
• Leading Coefficient: 𝑎1
• Leading Variable: 𝑥1
• Homogenous linear equation: 𝑏 = 0
• Non-homogeneous linear equation: 𝑏 ≠ 0
Linear equations have no products or roots of variables and no variables involved in trigonometric,
exponential or logarithmic functions.
Variables only appear to the first degree.
6/6/2023 4

5. Systems of Linear Equations
A system of m linear equations in n variables is a set of m linear equations:
𝑎11𝑥1 + 𝑎12𝑥2 + ⋯ + 𝑎1𝑛𝑥𝑛 = 𝑏1
𝑎21𝑥1 + 𝑎22𝑥2 + ⋯ + 𝑎2𝑛𝑥𝑛 = 𝑏2
… … …
𝑎𝑚1𝑥1 + 𝑎𝑚2𝑥2 + ⋯ + 𝑎𝑚𝑛𝑥𝑛 = 𝑏𝑚
 𝑎𝑖𝑗 is the coefficient of 𝑥𝑗 in the 𝑖th equation.
A system of linear equations has exactly one solution, an infinite number of solutions, or no
solution.
A system of linear equations is consistent if it has at least one solution and inconsistent if it has no
solution.
6/6/2023 5

6. Systems of Linear Equations
Inconsistent Consistent
No Solution
Unique Solution More than one
solution
6/6/2023 6

7. Systems With Two Unknowns
 Solution of system of two linear equations in two variables:
𝑎1𝑥 + 𝑏1𝑦 = 𝑐1
𝑎2𝑥 + 𝑏2𝑦 = 𝑐2
6/6/2023 7

8. Solving a System of Linear Equations
Row-echelon form follows a stair-step pattern and has leading coefficient of 1.
Using substitution to solve a system in row-echelon form.
6/6/2023 8
𝑥 − 2𝑦 + 3𝑧 = 9 Eq.1
𝑦 − 3𝑧 = 5 Eq.2
𝑧 = 2 Eq.3
 𝑧 = 2 is known from Eq.3.
 Substitute 𝑧 = 2 in Eq.2 to obtain 𝑦 = −1.
 Substitute 𝑧 = 2 and 𝑦 = −1 in Eq.1 to obtain 𝑥 = 1.

9. Gaussian Elimination and Gauss-Jordan Elimination
Definition of Matrix:
A matrix is a rectangular array of numbers (real or complex) arranged in rows and columns.
𝑎11 𝑎12 ⋯ 𝑎1𝑛
𝑎21 𝑎22 ⋯ 𝑎2𝑛
⋮ ⋮ ⋱ ⋮
𝑎𝑚1 𝑎𝑚2 ⋯ 𝑎𝑚𝑛
A matrix with m rows and n columns is said to be of size 𝑚 × 𝑛.
The entry 𝑎𝑖𝑗 is located in the 𝑖th row and 𝑗th column.
If 𝑚 = 𝑛, the matrix is called a square matrix of order 𝑛.
The entries 𝑎𝑖𝑗, 𝑖 = 𝑗 are called diagonal entries.
6/6/2023 9

10. Augmented/Coefficient Matrix
The matrix derived from the coefficients and constant terms of a system of linear equations is
called the augmented matrix of the system.
The matrix containing only the coefficients of the system is called the coefficient matrix of the
system.
System Augmented Matrix Coefficient Matrix
𝑥 − 2𝑦 + 3𝑧 = 9
−𝑥 + 3𝑦 = −4
2𝑥 − 5𝑦 + 5𝑧 = 17
6/6/2023 10
1 −2 3 9
−1 3 0 −4
2 −5 5 17
1 −2 3
−1 3 0
2 −5 5

11. Elementary Row Operation
Interchange two rows.
Multiply a row by a nonzero constant.
Add a multiple of a row to another row. 1 3
2 5 𝑅2+(−2)𝑅1→𝑅2
−2 −6
0 −1
Two matrices are said to be row equivalent if one can be obtained from another by a finite
sequence of elementary row operations.
6/6/2023 11
1 3
2 5 𝑅1↔𝑅2
2 5
1 3
1 3
2 5 (−2)𝑅1→𝑅1
−2 −6
2 5

12. Use of Elementary Row Operations to Solve a System
6/6/2023 12
𝑥 − 2𝑦 + 3𝑧 = 9
−𝑥 + 3𝑦 = −4
2𝑥 − 5𝑦 + 5𝑧 = 17
1 −2 3 9
−1 3 0 −4
2 −5 5 17
Linear System Associated Augmented Matrix
1 −2 3 9
−1 3 0 −4
2 −5 5 17
𝑅1+𝑅2→𝑅2
𝑅3+(−2)𝑅1→𝑅3
1 −2 3 9
0 1 3 5
0 −1 −1 −1
𝑅3+𝑅2→𝑅3
1 −2 3 9
0 1 3 5
0 0 2 4
0.5𝑅3→𝑅3
1 −2 3 9
0 1 3 5
0 0 1 2
𝑧 = 2
𝑦 − 3𝑧 = 5 ⇒ 𝑦 = −1
𝑥 − 2𝑦 + 3𝑧 = 9 ⇒ 𝑥 = 1

13. Row-Echelon form of a Matrix
A matrix in row-echelon form has the following properties:
• Rows of all zeros are at the bottom of the matrix.
• For each row that does not consist all of zeros, the first nonzero entry is 1 (called a
leading 1).
• Staircase pattern of first nonzero entries of each row (nonzero entries in each row are to
the right of the one above).
A matrix in row-echelon form is in reduced echelon form if every column that has a leading 1 has
zeros in every position above and below its leading 1.
Row-Echelon Form Not In Row-Echelon Form Reduced Row-Echelon Form
1 −3 5 2
0 1 3 −5
0 0 1 4
0 0 0 0
1 2 −3 4
0 2 1 −1
0 0 1 4
0 0 1 −3
1 0 0 −1
0 1 0 2
0 0 1 3
6/6/2023 13

14. Gaussian Elimination with Back -Substation
Write the augmented matrix of the system of linear equations.
Use elementary row operations to rewrite the augmented matrix in row-echelon form.
Write the system of linear equations corresponding to the matrix in row-echelon form, and use
back substitution to find the solution.
6/6/2023 14

15. System with Unique Solution
6/6/2023 15
𝑥2+ 𝑥3 − 2𝑥4 = −3
𝑥1+2𝑥2− 𝑥3 = 2
2𝑥1 + 4𝑥2 + 𝑥3 − 3𝑥4 = −2
𝑥1−4𝑥2 − 7𝑥3 − 𝑥 4 = 19
Solve the system
0 1 1 −2 −3
1 2 −1 0 0
2 4 1 −3 −2
1 −4 −7 −1 19
𝑅1↔𝑅2
1 2 −1 0 0
0 1 1 −2 −3
2 4 1 −3 −2
1 −4 −7 −1 19
𝑅3−2𝑅1
𝑅4−𝑅1
1 2 −1 0 0
0 1 1 −2 −3
0 0 3 −3 6
0 −6 −6 −1 −21
𝑅4+6𝑅1
1 2 −1 0 0
0 1 1 −2 −3
0 0 3 −3 6
0 0 0 −13 −39
𝑅3×(1/3)
𝑅4×(−1/13)
1 2 −1 0 0
0 1 1 −2 −3
0 0 1 −1 −2
0 0 0 1 3
𝑥4 = 3
𝑥3 − 𝑥4 = −2 ⇒ 𝑥3 = 1
𝑥2 + 𝑥3 − 2𝑥 4 = −3 ⇒ 𝑥2 = 2
𝑥1+2𝑥2− 𝑥3= 2 ⇒ 𝑥1 = −1

16. System with No Solution
6/6/2023 16
Solve the system
𝑥1− 𝑥2 + 2𝑥3 = 4
𝑥1+ 𝑥3= 6
2𝑥1−3𝑥2 + 5𝑥3 = 4
3 𝑥1−2𝑥2 − 𝑥3 = 1
1 −1 2 4
1 0 1 6
2 −3 5 4
3 −2 −1 1
𝑅′
2→𝑅2−𝑅1
𝑅′
3→𝑅3−2𝑅1
𝑅′
4→𝑅4−3𝑅1
1 −1 2 4
0 1 −1 2
0 −1 1 −4
0 5 −7 −11
𝑅′
3→𝑅3+𝑅2
1 −1 2 4
0 1 −1 2
0 0 0 −2
0 5 −7 −11
0 = −2
The original system of linear equations in inconsistent and the system has no solution.

17. System with Infinite Number of Solutions
6/6/2023 17
Solve the system
2𝑥 + 4𝑦 − 2𝑧 = 0
3𝑥 + 5𝑦 = 1
2 4 −2 0
3 5 0 1 (1/2)𝑅1→𝑅1
1 2 −1 0
3 5 0 1 𝑅2+(−3)𝑅1→𝑅2
1 2 −1 0
0 −1 3 1
(−1)𝑅2→𝑅2
1 2 −1 0
0 1 −3 −1 𝑅1+(−2)𝑅2→𝑅1
1 0 5 2
0 1 −3 −1
𝑥 + 5𝑧 = 2
𝑦 − 3𝑧 = −1
Leading Variable: 𝑥, 𝑦
Free Variable: 𝑧
Let 𝑧 = 𝑎, 𝑎 ∈ ℝ ⟹
𝑥 = 2 − 5𝑧 = 2 − 5𝑎
𝑦 = −1 + 3𝑧 = −1 + 3𝑎

18. Gauss-Gordan Elimination
6/6/2023 18
𝑥 − 2𝑦 + 3𝑧 = 9
−𝑥 + 3𝑦 = −4
2𝑥 − 5𝑦 + 5𝑧 = 17
⟹
𝑥 = 1
𝑦 = −1
𝑧 = 2
• Continues the reduction process until the reduced row-echelon form is obtained.
• Use Gauss-Jordan elimination to solve the system
1 −2 3 9
−1 3 0 −4
2 −5 5 17
𝑅1+2𝑅2→𝑅1
1 0 9 19
0 1 3 5
0 0 1 2
𝑅1+ −9 𝑅3→𝑅1
𝑅2+(−3)𝑅3→𝑅2
1 0 0 1
0 1 0 −1
0 0 1 2
Row-echelon form

19. Homogeneous System of Linear Equations
A system of linear equations is said to be homogenous if all the constant terms are zero.
𝑎11𝑥1 + 𝑎12𝑥2 + ⋯ + 𝑎1𝑛𝑥𝑛 = 0
𝑎21𝑥1 + 𝑎22𝑥2 + ⋯ + 𝑎2𝑛𝑥𝑛 = 0
… … …
𝑎𝑚1𝑥1 + 𝑎𝑚2𝑥2 + ⋯ + 𝑎𝑚𝑛𝑥𝑛 = 0
Every homogeneous system of linear equations is consistent.
Trivial Solution: All variables in a homogeneous system have the value zero, then each of the
equation must be satisfied.
If the system has fewer equations than unknowns, then it must have an infinite number of
solutions.
6/6/2023 19

20. Solution of Homogenous System
6/6/2023 20
Solve the homogeneous system of linear equations
𝑥1− 𝑥2 + 3𝑥3 = 0
2𝑥1+𝑥2 + 3𝑥3 = 0
1 −1 3 0
2 1 3 0 𝑅2+(−2)𝑅1→𝑅2
1 −1 3 0
0 3 −3 0 (1/3)𝑅2→𝑅2
1 −1 3 0
0 1 −1 0
𝑅1+𝑅2→𝑅1
1 0 2 0
0 1 −1 0
𝑥1+ 2𝑥3 = 0
𝑥2 − 𝑥3 = 0
Let 𝑥3 = 𝑎, 𝑎 ∈ ℝ ⟹
𝑥1 = −2𝑥3 = −2𝑎
𝑥2 = 𝑥3 = 𝑎
When 𝑎 = 0, 𝑥1, 𝑥2, 𝑥3 = 0 (trivial solution)

21. Applications of System of Linear Equations
6/6/2023 21