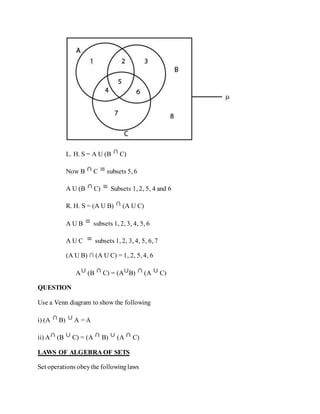
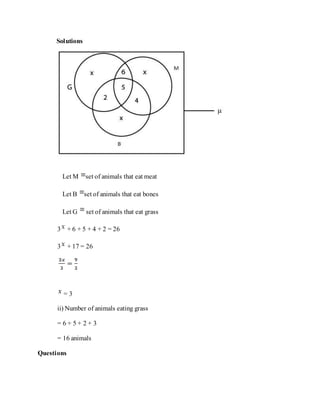
This document introduces some basic concepts of set theory: 1. Sets are collections of well-defined objects that can be represented using capital letters. Elements of a set are denoted using symbols like ∈ and ∉. 2. Important sets in number systems include real numbers (IR), positive/negative reals (IR+/IR-), integers (Z), positive/negative integers (Z+/Z-), rational numbers (Q), and natural numbers (N). 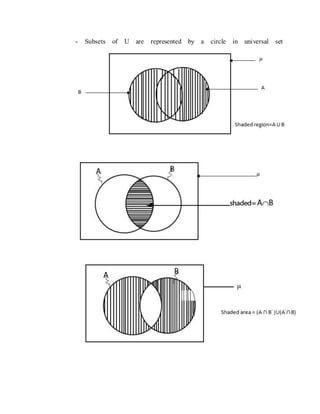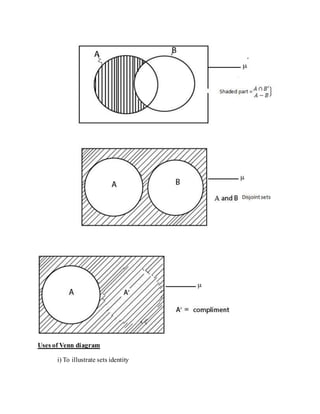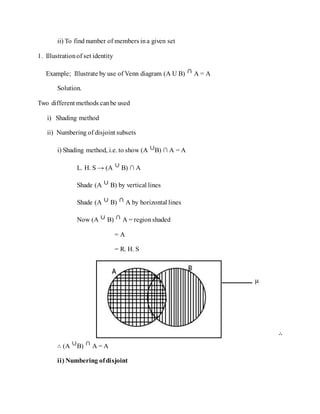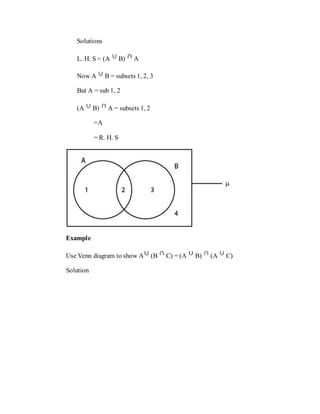3. Sets can be specified using a roster method that lists elements or a set-builder notation that describes elements. Operations on sets include union, intersection, complement, and symmetric difference.

1. SET THEORY
The word set is usedto denote a collectionof well definedobjects
 Set are denotedby capital letters e.g. A, B, C, D etc
 The statement ‘’ x is an element of A’’ or ‘’ x belongto A’’ is writtenas x ∈ A
If x is not an element of A, we write x A
Importance sets ofthe number system
IR: a set of real numbers (+, -) all numbers
IR+: Is a set of positive real numbers
IR-: Is a set of negative real numbers
Z: a set of integers. (+, -) whole numbers
Z+: a set of positive integers
Z-: a set of negative integers
Q: a set of rational numbers (rational ½ = 0.33333 – rational numbers, number repeats and
terminate
N: a set of natural number (positive numbers startingfrom 1, 2, 3…… countingnumbers)
SPECIFICATION OF A SET
There are two ways of specifyinga set;
1. List its members (roster method)
2. Describingits elementsbymathematical notationor actual words (builder notation).
Examples
1. Let A = specified in roster form, specify this by set builder
notation
Solution

2. A is a set of all prime numbers less than 15
2. Let B = specifiedbyset builder, specifyby roster form
Solution
Since x2 = 9, x = 3, x = -3
B =
The general form of set builder notation
A =
OR
A =
E.g. A =
QUESTIONS
1. Let A =
a) Is 10 ∈ A NO
b) Is 11 ∈ A NO
c) Is 13 ∈ A NO
d) List all elements of A
A =
2. Use the roster methodto specifythe followingsets
a) A = {x ∈ Z: x + 3 = 5}
x + 3 = 5; x = 5 – 3, x = 2
A =

3. b) B =
B =
c) C =
x = -0.5 and x = 0.5
C=
3. Specifythe followingin roster form
a) A = {y ∈ Z: y= 3K where K∈Z+ and K ≤ 6}
Solution
K =
Y =
A =
b) B =
y =
B =
BASIC CONCEPTS OF SET.
1. The set that does not containany element is calledan emptyset, donated by Φ or { }
2. Universal set is a set which contains all elements under consideration. It is denotedby µ.
3. Equality; two sets are equal if they have same elements
i.e. If A = and B =
4. Equivalent; two sets are equivalent if they have same number of elements
i. e A = and B = ∴A≡B

4. 5. Subsets; A is a subset of B if every member of A is also a member of B. It is denoted
by A B
6. Improper subset; suppose A = and B = A B
7. Proper subset. Suppose A = and B = A B
Note i) (an emptyset is subset of any set)
ii) A A (a set is subset of its own set)
Number of subsets inaset
Let S =
How many subsets does it have?
The subsets are: { }
→There are 8 subsets of S.
If A = and If B =
Subset of A are : Subsets of B are :
Number of subsets of A= 2 Number of subset of B = 4
If a set has n members, the number of subsets = 2n
THE POWER SET
Is a set which contains all subsets of the given sets
If A = , subsets are
Power set of A is given by S =
Given B =
The power set of B is given by

5. S =
OPERATION OF SETS
1. UNION
The union of two sets A and B is denotedby AUB
- AUB =
- Is a set which have elements of set Aor set B without repetition.
Examples
→If A = and B =
AUB =
→If A = and B =
AUB =
2. INTERSECTION
- Is a set which have both elements containedinset A and set B
A∩B = {x:x∈A and x∈B}
Examples
→If A = and B =
A B =
→If A = and B =
A B =
Here A and B are disjoint sets.

6. 3. COMPLEMENT
The complement of Set A denoted by A′ is the set of all elements which are in
universal set but not in A.
E.g. A =
µ=
A′ =
4. RELATIVE COMPLEMENT
Relative complement of A with respect to set B is denoted by A' B or A – B and is
definedas follows
A B =
Example
A =
B =
Then A B =
B A =
5. THE SYMMETRIC DIFFERENCE
All elements whichare either in set A or set B but not both
- The symmetric differenceof A and B is denotedby A B
A B =
Examples
A =
B =

7. A B =
QUESTIONS
1. List the subsets of the followingsets
a) A =
b) B =
2. Let A =
Write down the subsets of A
3. Whichof the followingare true and which are false?
a) Φ Φ b) 0 = Φ c) Φ∈ d) Φ ∈
4 . Let A =
a) Is ∈ A
b) Is 2 ∈ A
c) Is ∈ A
d) Is A
e) Is
f) Is
5. Let µbe the set of all positive integers, A is the set of all even integers and B is a set of all
odd integers. What are sets?
a) A B b) A B c) A B d) A’ e) B’ f) A B
QUESTIONS
1. Let µ be the universal set and Φ be an empty set. What are

8. a) Φ = µ
b) µ = Φ
c) µ – Φ = µ
d) Φ – µ = Φ
e) µ ∩ Φ = Φ
f) µ Φ = µ
2. Let A be subset of the universal set µ. What are the following?
a) A Φ = A
b) A A = A
c) A Φ = Φ
d) A A = A
e) A µ = A
f) A µ = µ
g) A ∩ A' = Φ or {}
h) A A'= µ
i) A µ = A'
j) A Φ = A
3. Let A and B be subsets of a universal set µ. Suppose A B. What are;
a) A U B = B
b) A B = A

9. SET INTERVAL ON THE NUMBER LINE
1. Let A = and B={x∈IR:-7< x ≤ 3}Represents these set intervals on two
separate number lines
Solutions
For A =
For B =
Examples
Using the sets A and B defined above, state and represents the following sets on same
number line
a) A B b) A′ c) B′ d) A U B′
Solutions
a) A B
A B =
b) A′

10. A′ =
c)B′
B′ =
a)
(d)A U B′
A U B′ =
QUESTION
i) Represent the above sets onone number line
ii) Draw and state each of the followingsets on separate number lines
a) A ∩ B b) A ∪B c) B′ d) A∩B′
Solution

11. (i)
(ii)(a) A
b) A U B
c) B′

12. QUESTIONS.
1. Represents andthen draw on one number line the followingset interval
Using the above set interval, represent andstate the following
i) A B ii) A C iii) C B' iv) (A B)
C
VENN DIAGRAMS
Sets can be representedinthe form of diagrams calledVenn diagrams
- The universal set is representedbya rectangle

13. - Subsets of U are represented by a circle in universal set

14. Uses of Venn diagram
i) To illustrate sets identity

15. ii) To find number of members ina given set
1. Illustrationof set identity
Example; Illustrate by use of Venn diagram (A U B) A = A
Solution.
Two different methods canbe used
i) Shading method
ii) Numbering of disjoint subsets
i) Shading method, i.e. to show (A B) ∩ A = A
L. H. S → (A B) ∩ A
Shade (A B) by vertical lines
Shade (A B) A by horizontal lines
Now (A B) A = regionshaded
= A
= R. H. S
∴ (A B) A = A
ii) Numbering ofdisjoint

16. Solutions
L. H. S = (A B) A
Now A B = subsets 1, 2, 3
But A = sub 1, 2
(A B) A = subsets 1, 2
=A
= R. H. S
Example
Use Venn diagram to show A (B C) = (A B) (A C)
Solution

17. L. H. S = A U (B C)
Now B C subsets 5, 6
A U (B C) Subsets 1, 2, 5, 4 and 6
R. H. S = (A U B) (A U C)
A U B subsets 1, 2, 3, 4, 5, 6
A U C subsets 1, 2, 3, 4, 5, 6, 7
(A U B) ∩ (A U C) = 1, 2, 5, 4, 6
A (B C) = (A B) (A C)
QUESTION
Use a Venn diagram to show the following
i) (A B) A = A
ii) A (B C) = (A B) (A C)
LAWS OF ALGEBRA OF SETS
Set operations obeythe followinglaws

18. 1. Commutative laws
A U B = B U A
A B = B A
2. Associative laws
a) (A U B) U C = A U (B U C)
b) (A B) C = A (B C)
3. Distributive laws
a) A U (B C) = (A U B) (A U C)
b) A (B U C) = (A B) (A C)
4. De -Morgan’s laws
a) (A U B)′ = A′ B′
b) (A B)′ = A′U B′
5. Identitylaws
a) A µ = µ
b) A µ = A
c) A Φ = A
d) A Φ =Φ
e) AΦ = A
f) AA = Φ
Examples
Use laws of algebra of set to simplify

19. 1. (A (A B)′)′
Solution
(A (A B)′)′ ≡(A (A′ B′))′ De-Morgan’s law
≡((A A′) B′ )′Associative law
≡ (Φ B′) Complement law
≡ (Φ)′Identity law
≡ µ complement law
(A (A U B)′)′ = µ
Examples
Use the laws of algebra of sets to prove
(A (B C′)) C = (A C) (B C)
Solution
L.H.S (A (B C′)) C
= (((A B) C′) C…….. Associative law
=((A B) U C) (C′ C) ………distributive law
= ((A B) C) (µ) …………complement law
= (A B) C……………. identitylaw
= (A C) (B C) ……………distributive law
= R. H. S
Exercise
1. Use laws of algebra of set to simply

20. i) (A B) (A B')
ii) (A' B') (A B)
iii) (A B) U (A – B)
iv) A (A B)
2. Use laws of algebra to prove
i) (Z W)′ W = Φ
ii) (X Y') (X Y) (Y X′) = X Y
iii) (A – B) A = A
Note
A – B = A B′ by definition
Number of elements inaset
The number of elements inset A is denotedby n (A)
Example
Let A be a set of all positive odd integers which are less than 10. Find n (A)
Solution
A = {1, 3, 5, 7, 9}
Now n (A) = 5
Examples
Let A ={x ∈ IR:x2-x-2=0}. Find n (A)
Solution

21. Note
i) The number of elements of aset is definedonly for a finite set
ii) If A U then the number of elements of A′ is n(A′) = n(µ) – n(A)
Example
If A U and B U then show that n (A B) = n(A) + n(B) – n(A B)
Proof
Refer to the Venn diagram below
Represents the number of elements in disjoint subset as follows
Let n (A B′) = a n (A′ B) =
c
n (A B) = b
R. H. S = n (A) + n (B) – n (A B)
= (a + b) + (b + c) – b

22. = a + 2b + c – b
= a + b + c
n (A B)
L. H. S
EXAMPLE
1. Given n (X) = 18, n (Y) = 26, n (X ∩ Y) = 12. Find n (X Y)
2. Given n (S T) = 19, n (s) = 15. n (S T′) = 10. Find n(S
T)
3. Given n (A B) = 15
n (A B) = 16
n ((A B)′) = 4
n (A – B) = 8
Find i) n (A) ii) n (A B′) iii) n (µ) iv) n (A′ B)
Solutions
1. n (X Y) = n (X) + n (Y) – n (X Y)
=18 + 26 – 12
= 32
n (X Y) = 32
2. n(S T) = 19, n(S) = 15, n(S T') = 10
i) n(S T) =?
n(S T) = n(S) – n(S T')

23. = 15 – 10
= 5
n( S T) = 5
3. n(A B) = 5, n(A B) = 16, n(A B)′ = 4, n(A – B) = 8
i) n(A) =? ii) n (A B′) iii) n(µ) iv) n (A′ B)
Solutions
n (A) = n(A – B) + n(A B)
= 8 + 5
= 13
ii) n (A B') = n (A) + n(B′)
= 13 + 4
= 17
n(A B') = 17
iii) n(µ) = n(A B) + n(( A B))′
= 16 + 4
= 20
n(µ) = 20
iv) n(A′ B) = n(B) – n(A B)
n(A′ B) = n(A B) – n(A) + n(A B) – n (n (A B))
n(A′ B) = 16 – 13
n (A′ B) = 3

24. 4. By using n (A B) = n(A) + n(B) – n(A B) show that;
n(A B C) = n(A) + n(B) + n(C) – n(A B) – n(A C) – n(B C) + n(A B
C)
Solutions
Let B C = K
L.H.S n(A B C) = n(A K)
= n(A) + n(K) – n(A K)
= n(A) + n(B C) – n(A (B C))
= n(A) + n(B) + n(C) – n(B C) – n((A B) (A C))
= n(A) + n(B) + n(C) – n(B C) – (n(A B) + n( A C) – n((A
B) (A C))
= n(A) + n(B) + n(C) – n(B C) – n(A B) – n(A C) + n(A B
C)
Questions
There are 26 animals in zoo, 5 animals eat all type of food in the zoo i.e. grass, meat
and bones. 6 animals eat grass and meat only, 2 animals eat grass and bones only, 4
animals eat meat and bones only. The number of animals eating one type of food only
is divided equally betweenthe three types of food.
i) Illustrate the above informationby a labeledVenn diagram
ii) Find the number of animals eating grass

25. Solutions
Let M set of animals that eat meat
Let B set of animals that eat bones
Let G set of animals that eat grass
3 + 6 + 5 + 4 + 2 = 26
3 + 17 = 26
= 3
ii) Number of animals eating grass
= 6 + 5 + 2 + 3
= 16 animals
Questions

26. 1. A class has 15 boys and 15 girls. In the class 20 students are studying science, 14 students
are studying math, 10 boys are studying science, 10 boys are studying math, 8 boys are
studying bothmath and science, 4 girls are studying neither math nor science.
Find i) How many students study math only?
ii) How many students study science only?
iii) How many students study bothmath and science?
2. In a class of 35 students each students each student takes either one of two
subjects (physics, chemistry and biology). If 13 students take chemistry, 22 students take
physics,17 students take biology, 6 students take both physics and chemistry and 3
students take both biology and chemistry. Find the number of students who take both
biology and physics.
Solutions
Since there are 15 girls
10 – + + 4 – + 4 = 15
18 – = 15
= 3

27. i) Students who study math only = 2 + 1
= 3 students
ii) Students who study science only= 2 + 7
= 9 students
iii) Students who study both math and science = 8 + 3
= 11 students
QUESTIONS
1. In a certain college apart from other discipline, no students is allowed to study less than
two of the subjects, finance, accounting and economics, 150 students study finance, 110
study accounting, 80 study economicsand 20 study three subjects
i) How many students study two of the named subjects?
ii) How many study finance or accounting or economic?
2. One poultry farm in Dar produces three types of chicks and in six months report revealed
that out of 126 of its regular customers, 65 bought broilers, 80 bought layers and 75 bought
cocks, 45 bought layers and cocks, 35 bought broilers and cocks, 10 bought broilers only, 15
bought layers only and bought cocks only, 6 of the customers didnot show up.
i) How many customers bought all the three products?
ii) How many customers bought exactlytwo of the products?
3. An investigator was paid sh. 100 per person interviewed about their likes and dislikes on a
drink for lunch. He reported 252 responded positively coffee, 210 liked tea, 300 liked soda,
80 liked tea and soda, 60 liked coffee and soda. 50 liked all three, while 120 people said they
not like any drink at all. How much should the investigator be paid coffee andtea 60 people?