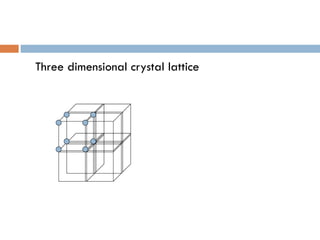
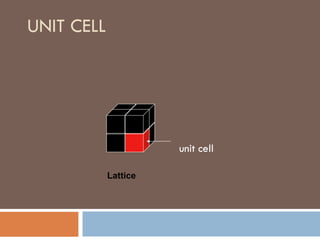
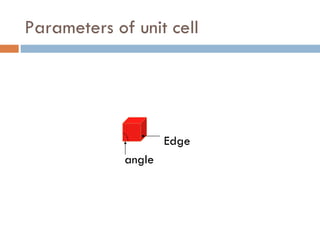
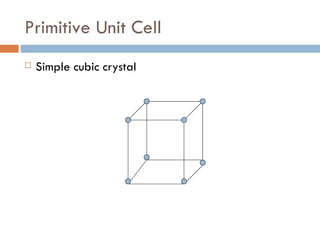
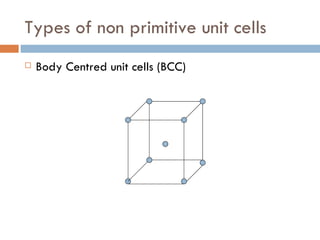
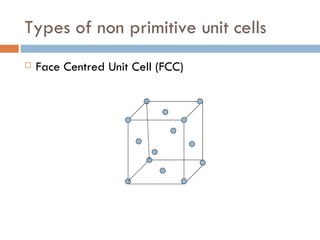
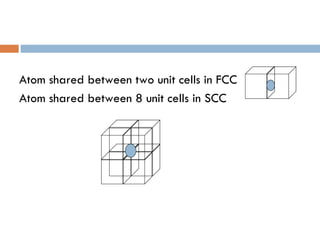
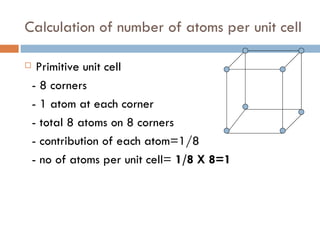
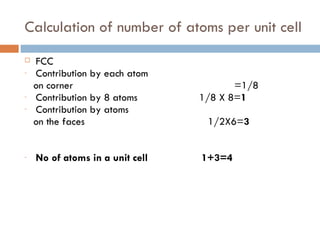
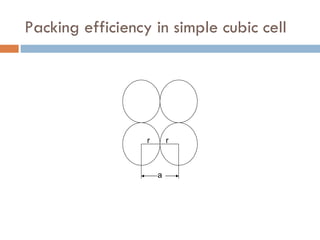
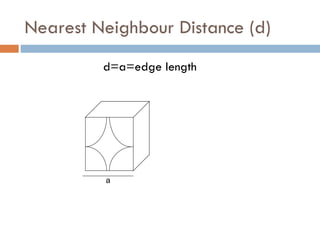
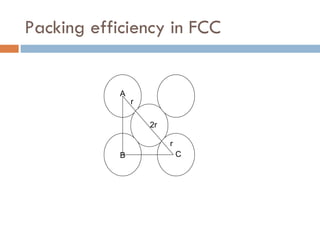
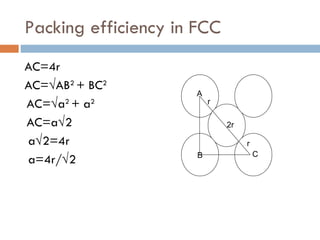
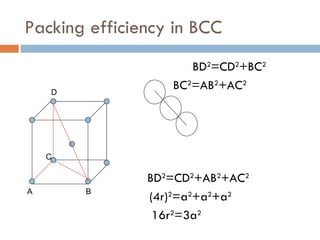
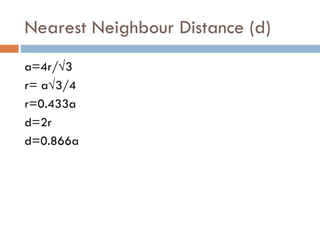
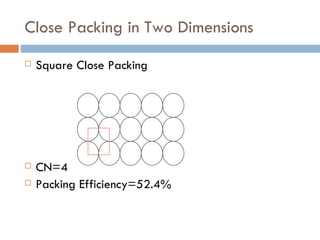
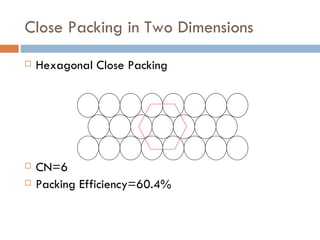
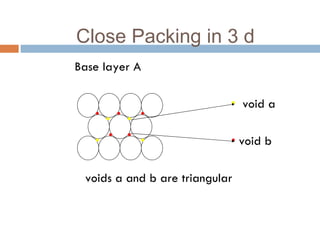
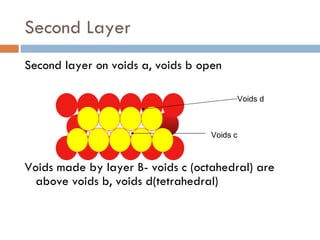
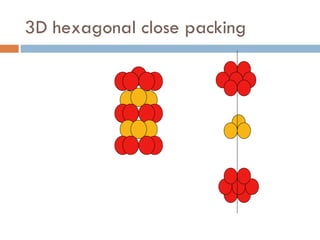
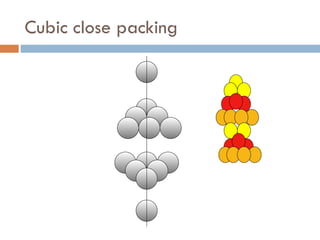
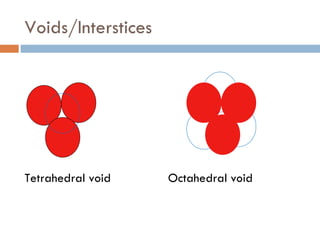
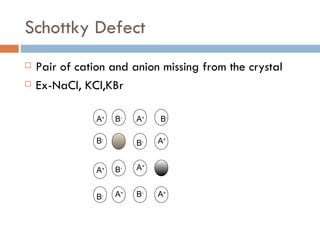
The document discusses different types of crystal defects including point defects, stoichiometric defects, and non-stoichiometric defects. Stoichiometric defects include Schottky and Frenkel defects which involve cation-anion pairs missing or cation dislocations. Non-stoichiometric defects result from deviations from the ideal ratio of cations to anions and include metal excess or deficiency defects involving anion or cation vacancies. Common examples of different defect types in various crystals are provided.

1. States Of Matter Gaseous State Liquid State Solid State

2. Solid State Form of matter that has a definite shape and volume and is rigid. Low compressibility High density Very slow diffusion Low vapour pressure

3. Classification of Solids Crystalline Solids Building entities are arranged in regular geometric pattern Sharp melting point Definite geometrical shape Possess cleavage planes Exhibit anisotropy Possess crystal symmetry

4. Classification of Solids Amorphous Solids Shapeless Building entities are randomly present No definite MP No cleavage planes Exhibit isotropy No symmetry

5. Crystal Lattice/ Space Lattice The regular repeating arrangement of points representing the constituent particles in three dimensional space Each point in a lattice represents a constituent particle-atom/ion/molecule Such point is called lattice point/lattice site

6. Three dimensional crystal lattice

7. UNIT CELL unit cell Lattice

8. Unit Cell Fundamental building block of space lattice Smallest 3-d portion of a complete space lattice which when repeated in different directions produces the whole space lattice

9. Parameters of unit cell Edge angle

10. Types of unit cells 1.Primitive Unit Cells/ simple unit cells - Particles are present only at the corners 2. Non primitive/ Centred unit cells - Particles are present at corners as well as at other positions within the unit cell

11. Primitive Unit Cell Simple cubic crystal

12. Types of non primitive unit cells Body Centred unit cells (BCC)

13. Types of non primitive unit cells Face Centred Unit Cell (FCC)

14. Atom shared between two unit cells in FCC Atom shared between 8 unit cells in SCC

15. Calculation of contribution of particles per unit cell An atom at a corner is shared by eight unit cells. Contribution of an atom per unit cell = 1/8 An atom at a face is shared by two unit cells. Contribution of an atom per unit cell = ½ An atom at the centre of body of unit cell is not shared by any other atom Contribution of an atom per unit cell = 1

16. Calculation of number of atoms per unit cell Primitive unit cell - 8 corners - 1 atom at each corner - total 8 atoms on 8 corners - contribution of each atom=1/8 - no of atoms per unit cell= 1/8 X 8=1

17. Calculation of number of atoms per unit cell BCC Contribution by each atom on corner=1/8 Contribution by 8 atoms = 1/8 X 8= 1 Contribution by atom within the body = 1 No of atoms in a unit cell = 1+1=2

18. Calculation of number of atoms per unit cell FCC Contribution by each atom on corner =1/8 Contribution by 8 atoms 1/8 X 8= 1 Contribution by atoms on the faces 1/2X6= 3 No of atoms in a unit cell 1+3=4

19. Packing Fraction/Efficiency Fraction of total volume of the unit cell occupied by the atoms present in it-Pck Fraction Percentage of total space filled by particles- Pck Efficiency

20. Packing efficiency in simple cubic cell r r a

21. Packing efficiency in simple cubic cell No of particles per unit cell = 1 Vol of particle =4/3 π r 3 Vol of cube =a 3 =(2r) 3 =8r 3 Packing fraction = 4/3 π r 3 ÷8r 3 = π /6 =0.524 Packing efficiency =52.4%

22. Nearest Neighbour Distance (d) d=a=edge length a

23. Packing efficiency in FCC B A C r r 2r

24. Packing efficiency in FCC AC=4r AC= √AB 2 + BC 2 AC=√a 2 + a 2 AC=a√2 a√2=4r a=4r/√2 B A C r r 2r

25. Packing efficiency in FCC Vol of unit cell = a 3 = 3 4r/√2 = 32r 3 /√2

26. No of spheres in the unit cell =4 Vol of 4 spheres =4X4/3 π r 3 =16/3 π r 3 Packing fraction =16/3 π r 3 ÷32r 3 /√2 = π √2/6 =0.74 Packing efficiency= 74% Packing efficiency in FCC

27. Nearest Neighbour Distance (d) a=4r/√2 a√2/4=r; r=0.3535a d=2r d=2X0.3535a d=0.707a a

28. Packing efficiency in BCC BD 2 =CD 2 +BC 2 but BC 2 =AB 2 +AC 2 BD 2 =CD 2 +AB 2 +AC 2 (4r) 2 =a 2 +a 2 +a 2 16r 2 =3a 2 D B C A

29. Packing efficiency in BCC 16r 2 =3a 2 a=(16r 2 /3) 1/2 a=4r/ √3 Vol of cube=a 3 Vol of unit cell=( 4r/ √3) 3 No of spheres in BCC=2 Vol of one sphere= 4/3 π r 3 Vol of two spheres= 8 /3 π r 3 Packing fraction=8 /3 π r 3 ÷64r 3 /3√3 = 0.68 = 68%

30. Nearest Neighbour Distance (d) a=4r/ √3 r= a √3/4 r=0.433a d=2r d=0.866a

31. Density Of A Crystal Density of cubic crystal of elements ρ =mass of unit cell÷vol of unit cell ρ = Z X M÷N A a 3 g/cm 3 Z= No of atoms per unit cell M= atomic mass of the element convert pm to cm using- 1pm=10 -10 cm

32. Packing in crystal lattices Close packing in 2d Square close packing Hexagonal close packing Close packing in 3d - cubic close packing (ccp) - hexagonal close packing (hcp)

33. Close Packing in Two Dimensions Square Close Packing CN=4 Packing Efficiency=52.4%

34. Close Packing in Two Dimensions Hexagonal Close Packing CN=6 Packing Efficiency=60.4%

35. Base layer A void a void b voids a and b are triangular Close Packing in 3 d

36. Second Layer Second layer on voids a, voids b open Voids made by layer B- voids c (octahedral) are above voids b, voids d(tetrahedral) Voids c Voids d

37. Third layer Depending on the arrangement of the third layer, packing may be Hexagonal close packing spheres of the third layer fit into voids d made by layer B ie exactly in line with spheres of layer A ABABAB…. Coordination No-12 (six of same layer, 3 from upper layer,3 from lower layer)

38. 3D hexagonal close packing

39. Cubic close packing Third layer C –spheres occupy voids c Spheres are neither aligned with layer A nor with B Spheres of fourth layer are aligned with layer A Unit cell of such lattice is FCC CN no=12, 6 in one plane,3 each in planes above and below.

40. Cubic close packing

41. HCP and CCP Packing efficiency=74% Ex- HCP-crystals of Mo,Mg,Be,Cd,Zn,Ti Ex-CCP-crystals of Fe,Ni,Ag,Au,Al

42. Voids/Interstices Tetrahedral void Octahedral void

43. Voids/Interstices The unoccupied/vacant space present in the lattice of a crystal Types- Tetrahedral-vacant space surrounded by four nearest neighbours in tetrahedral position Every void is surrounded by 4 particles 8 voids are present around each particle. Hence, no. of tetrahedral voids is twice the number of constituent particles

44. Voids/Interstices -Octahedral voids- Vacant space surrounded by six nearest neighbours in octahedral arrangement Each oct void is surrounded by 6 particles 6 voids around each particle No of oct voids=no of constituent particles

45. Radius Ratio of voids The ratio of radius of a void to that of a particle For a tetrahedral void- r/R=0.225 Limiting radius- a tetrahedral void can accommodate a particle of radius less than 0.225 only

46. Voids/Interstices Octahedral void- r/R=0.414 Limiting radius=0.414

47. Defects/Imperfections in crystals Ideal Crystal- same unit cell containing same lattice points throughout the lattice Difficult to obtain above 0 K Deviation from an ordered arrangement- Defect

48. Atomic Defects/Point Defects Due to irregularity in arrangement of atoms Atoms are missing OR Atoms are dislocated

49. Atomic Defects/Point Defects Stoichiometric Defects- ratio between cations and anions remains undisturbed Non stoichiometric Defects- ratio of cation and anion differs from the chemical formula Impurity Defects

50. Stoichiometric defects Types- Schottky defect Frenkel defect (dislocation defect)

51. Schottky Defect Pair of cation and anion missing from the crystal Ex-NaCl, KCl,KBr A + A + A + A + A + A + A + B - B - B - B - B - B - B -

52. Frenkel Defect Dislocation of cation into a vacancy Ex- ZnS, AgBr, AgCl A + A + A + A + A + A + A + B - B - B - B - B - B - B - A + B -

53. Non Stoichiometric Defects Types- Metal excess defect due to anion vacancies (F-centre or farbe centre defect) Ex- LiCl, KCl paramagnetic coloured A + A + A + A + A + A + A + A + B - B - B - B - B - B - B - e -

54. Non Stoichiometric Defects Metal excess due to interstitial cation Ex-ZnO e - A + A + A + A + A + A + A + A + A + B - B - B - B - B - B - B - B -

55. Non Stoichiometric Defects Metal deficiency due to cation vacancy Ex-FeS, FeO, NiO A + A 2+ A + A + A + A + A + B - B - B - B - B - B - B - B -