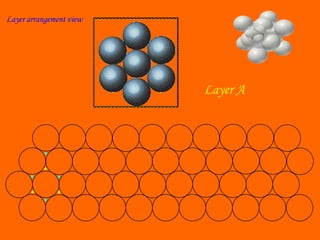
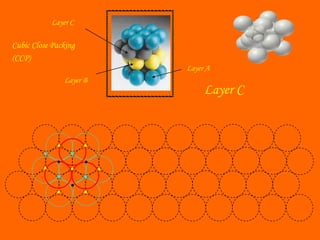
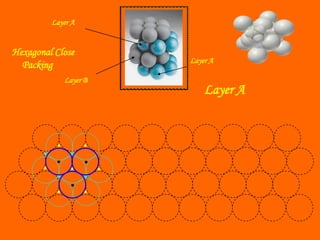
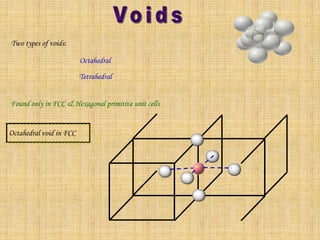
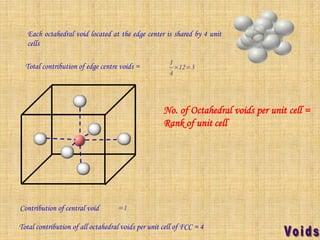
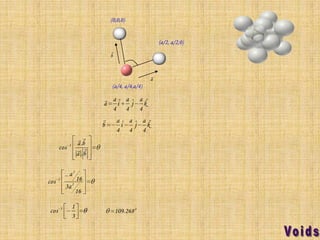
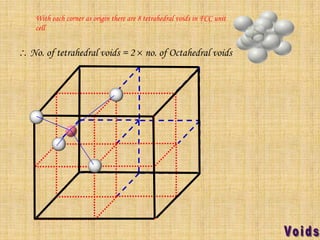
This document summarizes different types of crystal systems and lattice structures, including cubic, orthorhombic, rhombohedral, tetragonal, triclinic, and hexagonal systems. It also describes common Bravais lattices like primitive, FCC, and BCC. Finally, it discusses packing of layers in cubic close packing and hexagonal close packing, and defines octahedral and tetrahedral voids that can exist in FCC and hexagonal unit cells.

1. Crystal Systems
Cubic
Orthorhombic
Rhombohedral
Tetragonal
Triclinic
Hexagonal
Monoclinic
Bravais Lattices
Primitive, FCC, BCC
Primitive, FC, BC, EC
Primitive
Primitive, BC
Primitive
Primitive
Primitive, EC

2. Layer A
Layer arrangement view

3. Layer B

4. Layer C
Layer A
Layer B
Layer C
Cubic Close Packing
(CCP)

6. Layer A
Layer arrangement view

7. Layer B

8. Layer A
Layer A
Layer B
Layer A
Hexagonal Close
Packing

9. Unit Cell shape view
Unit Cell arrangement view

10. Packing Fraction depends on:
1. Layout of each layer
2. Placement of one layer over the other

11. Two types of voids:
Octahedral
Tetrahedral
Found only in FCC & Hexagonal primitive unit cells
Octahedral void in FCC

12. Each octahedral void located at the edge center is shared by 4 unit
cells
Total contribution of edge centre voids = 312
4
1

Contribution of central void 1
Total contribution of all octahedral voids per unit cell of FCC = 4
No. of Octahedral voids per unit cell =
Rank of unit cell

13. Tetrahedral void in FCC
(0,0,0)
x-axis
y-axis
z-axis
(a/2, a/2,0)
(a/2, 0,a/2)
(0, a/2,a/2)
(a/4, a/4,a/4)

14. (0,0,0)
(a/2, a/2,0)
(a/4, a/4,a/4)
a

b

k
a
j
a
i
a
a ˆ
4
ˆ
4
ˆ
4


k
a
j
a
i
a
b ˆ
4
ˆ
4
ˆ
4












ba
ba


.
.
cos 1









16
3
16cos 2
2
1
a
a




3
1
cos 1 o
268.109

15. With each corner as origin there are 8 tetrahedral voids in FCC unit
cell
 No. of tetrahedral voids = 2  no. of Octahedral voids