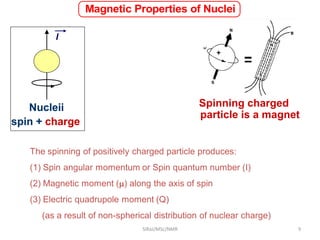
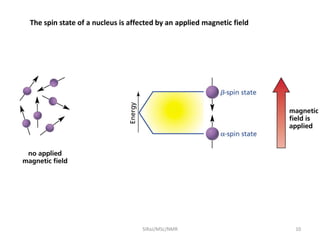
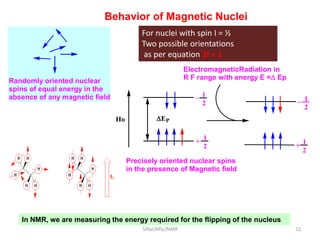
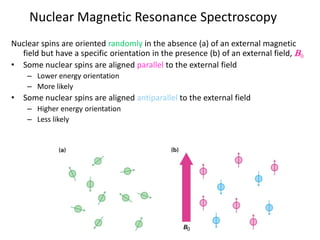
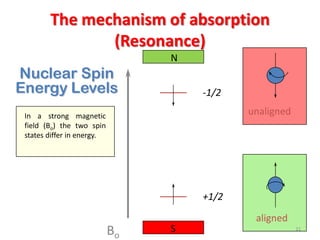
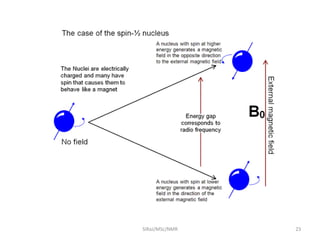
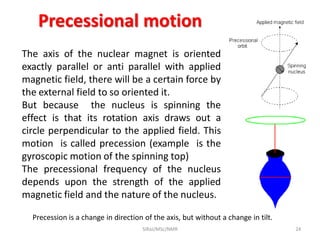
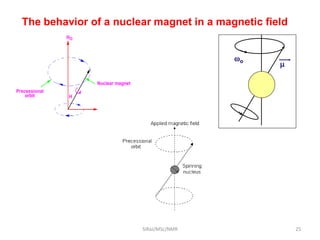
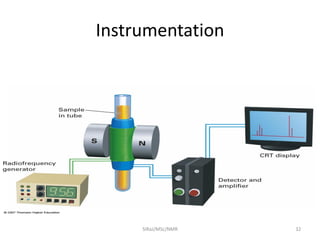
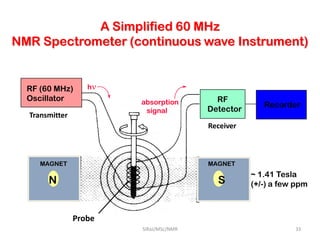
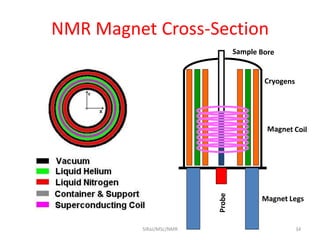
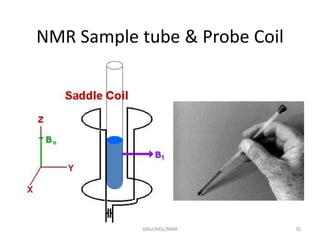
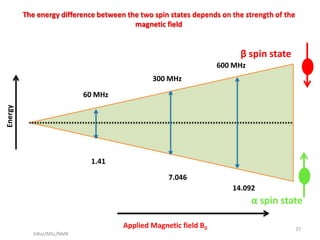
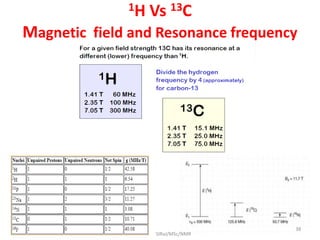
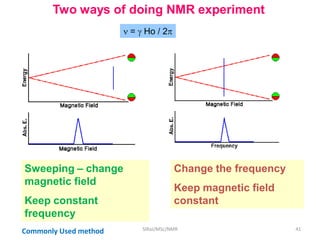
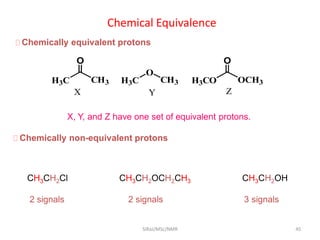
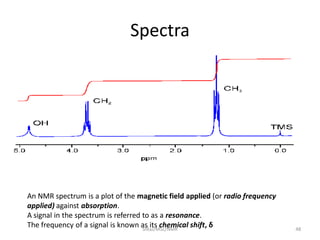
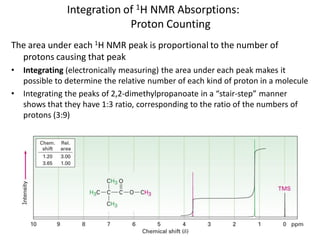
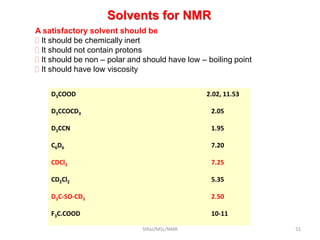
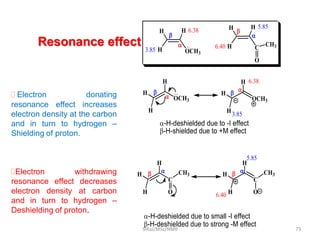
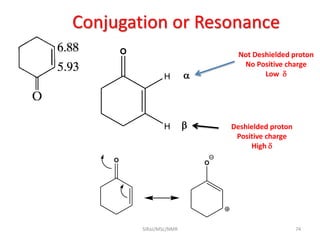
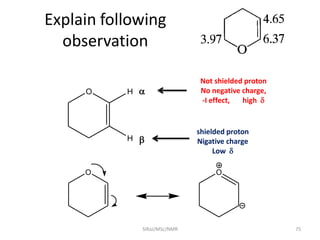
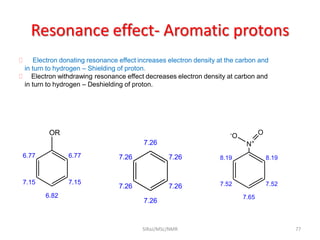
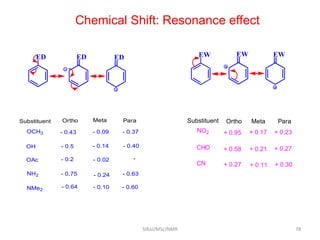
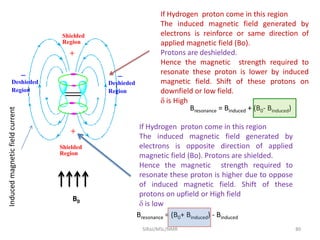
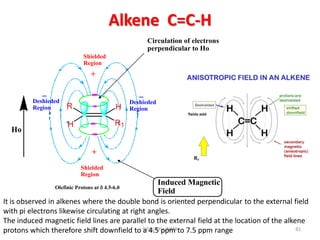
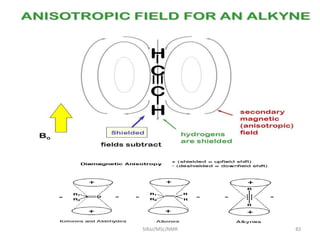
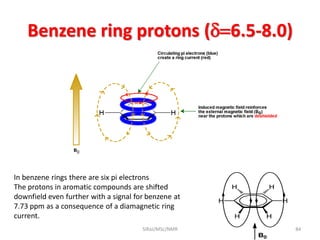
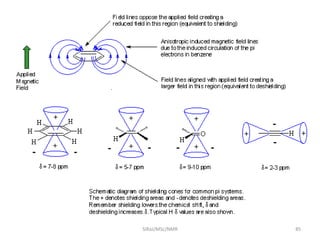
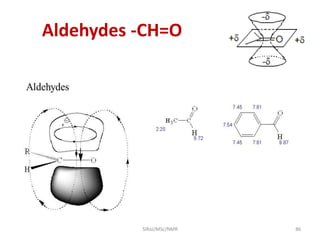
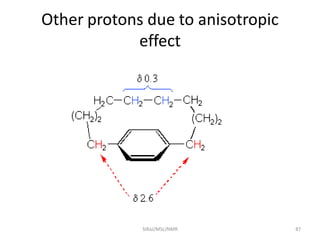
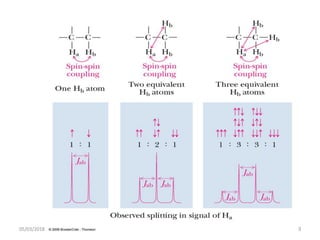
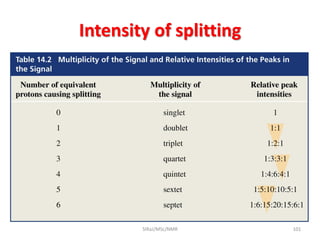
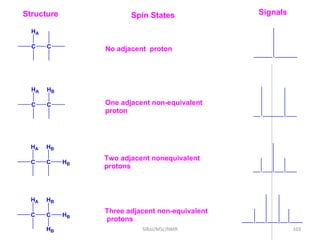
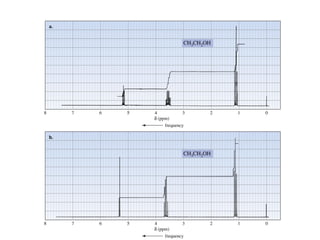
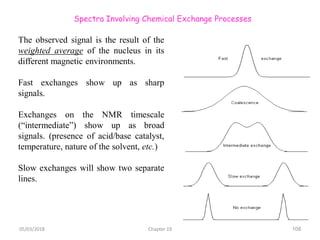
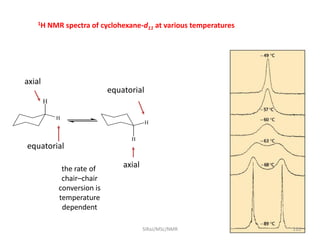
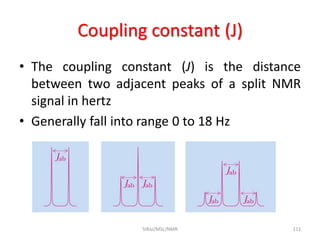
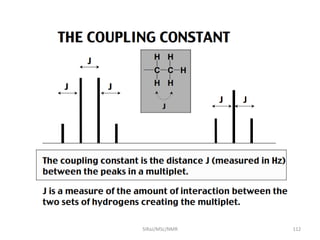
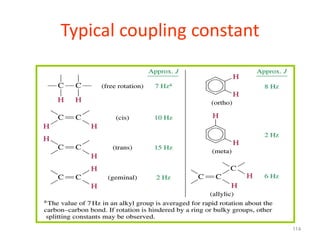
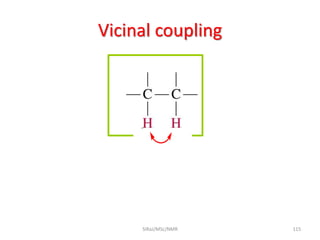
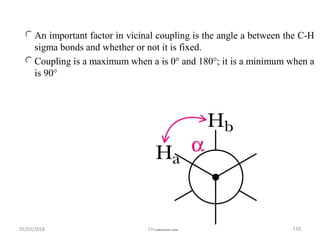
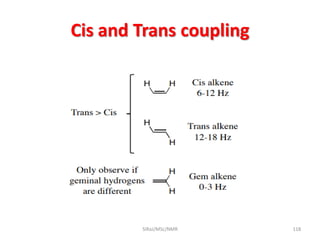
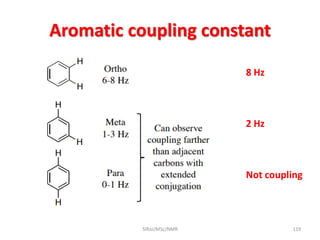
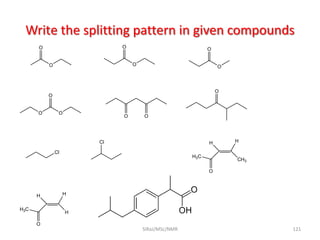
The document provides a summary of the history and development of Nuclear Magnetic Resonance (NMR) Spectroscopy. Some key points include:
1. NMR was first predicted in 1937 and first observed on bulk samples in 1946. Important early developments included 2D NMR in 1975 and NMR metabolomics in 1984.
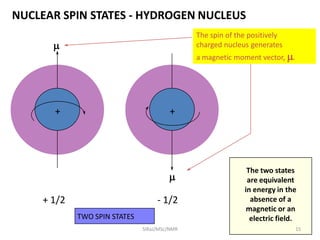
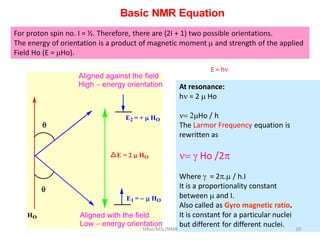
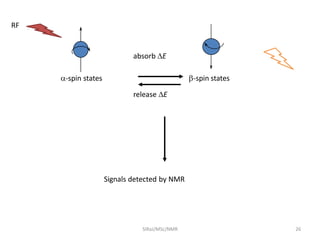
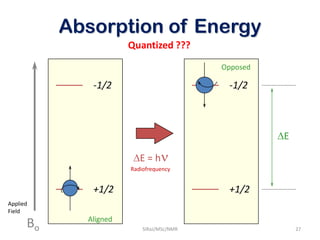
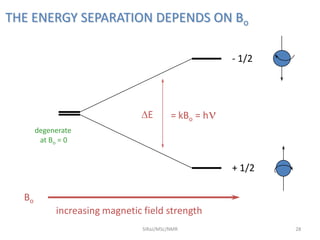
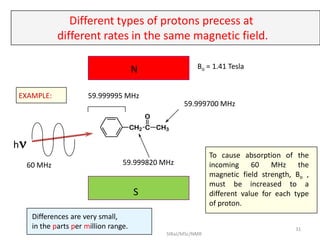
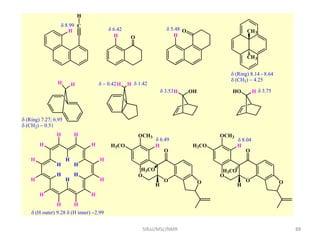
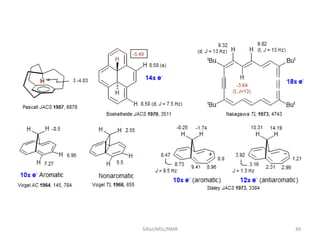
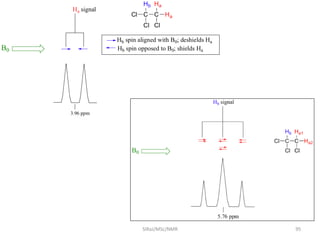
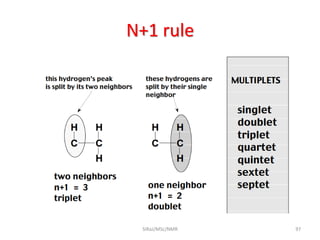
2. NMR utilizes the magnetic properties of certain atomic nuclei to determine structural information about molecules. It provides information about the number and type of hydrogen atoms, as well as their electronic environment.
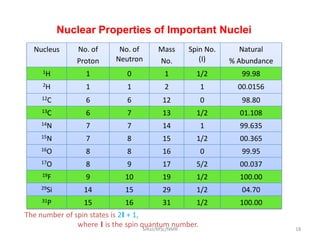
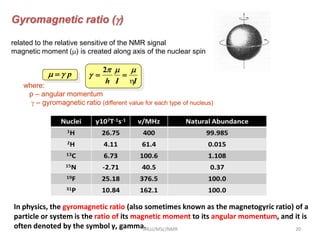
3. For a nucleus to be observable by NMR, it must have a non-zero spin quantum number and magnetic moment, and be spherical in shape. Common nuclei studied include 1H, 13C, 19