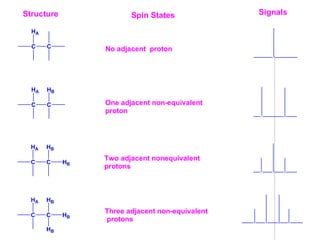
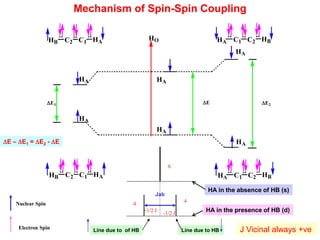
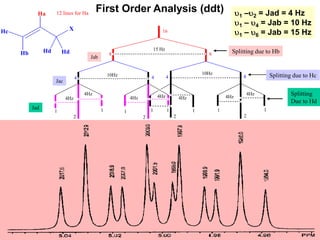
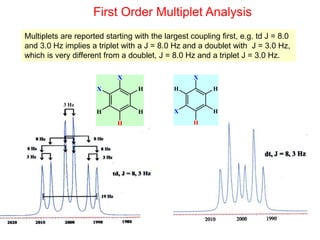
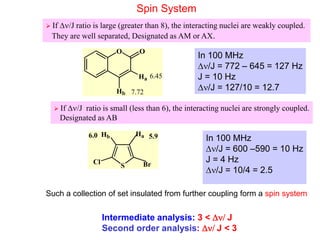
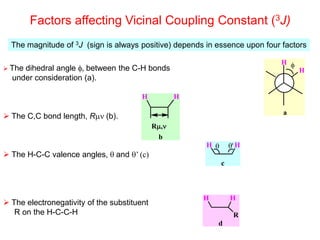
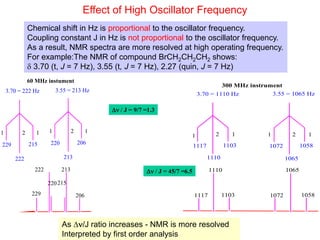
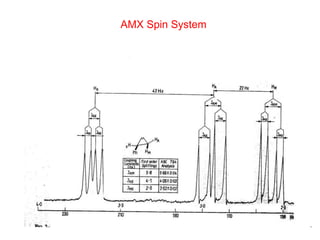
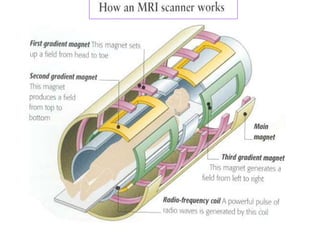
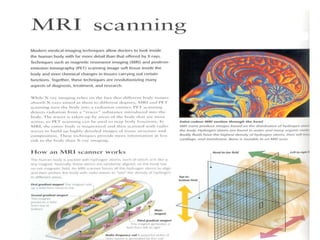
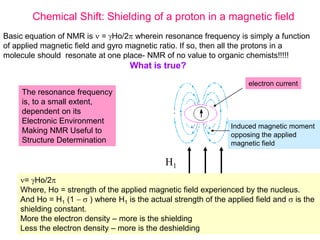
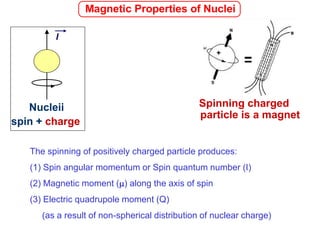
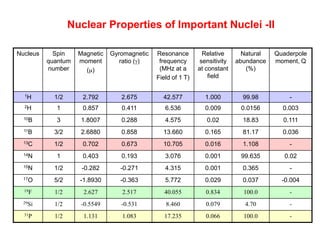
1. The document discusses the basic principles of Nuclear Magnetic Resonance (NMR) spectroscopy. It explains how certain nuclei can have spin and magnetic moments, and how these nuclei absorb electromagnetic radiation in the radiofrequency region when in a strong magnetic field. 2. The key parameters that determine whether a nucleus can be observed by NMR are discussed, including spin quantum number, magnetic moment, natural abundance, and quadrupole moment. Common nuclei observed by NMR like 1H, 13C, 19F, and 31P are described. 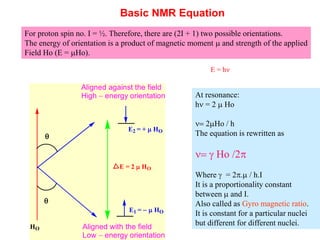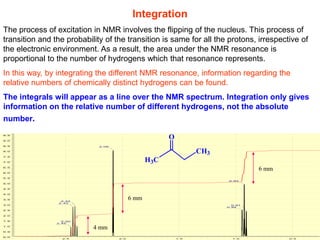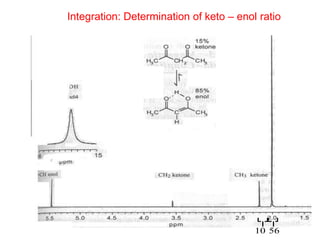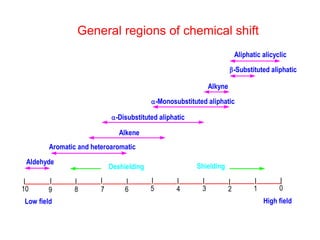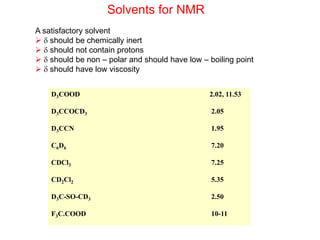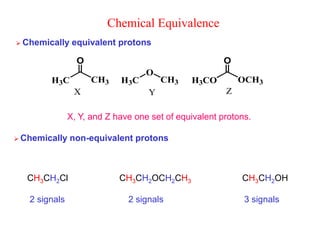3. The basic NMR equation is presented, showing the relationship between resonance frequency, magnetic field strength, and the gyromagnetic ratio. Important NMR parameters like chemical shift, integration, and

1. 2. 60 2. 50 2. 40 2. 30 2. 20 2. 10 2. 00 1. 90 1. 80 1. 70 1. 60 1. 50 1. 40 1. 30 1. 20 1. 10 1. 00 0. 90 0. 80
0. 0
0. 5
1. 0
1. 5
2. 0
2. 5
3. 0
3. 5
4. 0
4. 5
CH3
O
C
H3
Nuclear Magnetic Resonance Spectroscopy
Basic Principles
Dr. Gurumeet C wadhawa
Department of Chemistry
Karmaveer Bhaurao Patil College Vashi

2. Spectroscopy
Study of the interaction of light with matter
Light: Visible part of a large range of Electromagnetic Radiation
having Particle as well as wavelike properties.
Energy E = hn ( h = Plank’s constant 6.62 x 10 –27 erg/sec)
Ultra-
Violet
Visible Infra-Red
Near Far
Microwave Radio
Cosmic and
Gamma Rays
A0 10-4 1000 2000 4000 8000 104 107 1014
Nuclear
Transition
Electronic
Transitions
Molecular
Vibrational
Transitions
Molecular
Rotational
Transitions
Nuclear Spin
Transitions
Energy cal/mole
1014 – 1010 100 – 35 K ~28.5 K 10-2 – 10-6

3. Sample at
Equilibrium
Radiation
Excited State Spectrum
Relaxation
Observation
Spectroscopy
UV-Visible: Presence of chromophoric system/conjugation in the
molecules
IR Spectroscopy: Presence of Functional Groups in the molecules
1H NMR Spectroscopy:
The number of different types of Hydrogens in the molecules
The relative numbers of different types of Hydrogens in the molecules
The electronic environment of different types of Hydrogens in the molecules
The “neighbours to the neighbours” of the functional group
These spectroscopic techniques are mutually complimentary and a
combination of these three-along with a Mass Spectroscopy form a
powerful device in the determination of structures of organic molecules.

4. History of NMR Spectroscopy
1945 - The phenomenon was simultaneously discovered by two groups:
Purcell, Torrey and Pound at Harvard University: Paraffin
Bloch, Hansen and Packard at Stanford University: Water
1950 – The first NMR spectra of ethyl alcohol was recorded by Arnold,
Dharmatti and Packard.
1952 – The two discoverers (Bloch and Purcell) were awarded the
First Nobel Prize in NMR (Physics).
1991 – The second Nobel Prize in NMR (Chemistry) was awarded to
Richard Ernst for discoveries of advanced methodologies.
2002 – The third Nobel Prize in NMR (Chemistry) was awarded to
Kurt Wuthrich for determination of structures of Biomolecules
in solution by NMR.
2003 – Nobel Prize (Medicine) was awarded to Paul Lauterbur and Sir Peter
Mansfield for Magnetic Resonance Imaging.

5. Behavior of Magnetic Nuclei
Randomly oriented nuclear
spins of equal energy in the
absence of any magnetic field
1
2
_
1
2
+
EP
1
2
_
1
2
+
ElectromagneticRadiation in
R F range with energy E = Ep
Ho
Precisely oriented nuclear spins
in the presence of Magnetic field
For nuclei with spin I = ½
Two possible orientations
as per equation 2I + 1
In NMR, we are measuring the energy required for the flipping of the nucleus

6. l
Nucleii
spin + charge
l
Nucleii
spin + charge
l
l
Nucleii
spin + charge
Spinning charged
particle is a magnet
Spinning charged
particle is a magnet
Magnetic Properties of Nuclei
The spinning of positively charged particle produces:
(1) Spin angular momentum or Spin quantum number (I)
(2) Magnetic moment (m) along the axis of spin
(3) Electric quadrupole moment (Q)
(as a result of non-spherical distribution of nuclear charge)

7. The angular momentum of spinning nucleus is described in terms of spin quantum no.I
The spin quantum no. I is a characteristic constant of a nucleus, and is dependent on the
number of protons and neutrons.
1) Nuclei with odd mass number and odd or even no. of protons have
half – integral spin such as 1/2, 3/2, 5/2 etc.
2) Nuclei with even mass number and odd no. of protons have integral spin
such as 1, 2, 3
3) Nuclei with even mass number and even no.of protons always have zero spin
(Due to pairing of oppositely directed spins in the nucleus)
In general three rules apply to the nuclear spins.

8. Nucleus No. of
Proton
No. of
Neutron
Mass
No.
Spin
No. (I)
Natural
% Abundance
1H 1 0 1 1/2 99.98
2H 1 1 2 1 00.0156
11B 5 6 11 3/2 81.17
12C 6 6 12 0 98.80
13C 6 7 13 1/2 01.108
14N 7 7 14 1 99.635
15N 7 8 15 1/2 00.365
16O 8 8 16 0 99.95
17O 8 9 17 5/2 00.037
19F 9 10 19 1/2 100.00
29Si 14 15 29 1/2 04.70
31P 15 16 31 1/2 100.00
Nuclear Properties of Important Nuclei - I

9. Requirements of nuclei to be NMR active
Three important characteristics:
 Nuclei should have Spin no. I > 0 and magnetic momemtum m > 0
 Nuclei should have even charge distribution that is nucleus should be
spherical in shape so as Q = 0.
 Nuclei should have high % of natural abundance
1H, 13C, 19 F and 31 P nuclei have I = 1/2 and m > 0
These nuclei are spherical in shape (even charge distribution) and Q = 0
So observed by NMR technique.
1H, 19F and 31P have high % abundance
12C and 16O nuclei are also spherical in shape Q = 0; but I = 0 and m = 0
So non-magnetic and not observed by NMR
2H, and 14N nuclei have I > 0; m > 0 and Q > 0
Nuclei are ellipsoidal prolate in shape, so no even charge
distribution. So difficult to study by NMR
Ellipsoidal oblate
35Cl
Ellipsoidal prolate

10. Basic NMR Equation
For proton spin no. I = ½. Therefore, there are (2I + 1) two possible orientations.
The energy of orientation is a product of magnetic moment m and strength of the applied
Field Ho (E = mHo).
At resonance:
hn = 2 m Ho
n= 2mHo / h
The equation is rewritten as
n=  Ho /2
Where  = 2.m / h.I
It is a proportionality constant
between m and I.
Also called as Gyro magnetic ratio.
It is constant for a particular nuclei
but different for different nuclei.


HO
E2 = + m HO
E1 =  m HO
Aligned with the field
Low  energy orientation
Aligned against the field
High  energy orientation
E = 2 m HO
E = hn

11. Precessional
orbit
Nuclear magnet
HO
H
The behaviour of a nuclear magnet in a magnetic field
wo
m

12. Two ways of doing NMR experiment
Sweeping – change
magnetic field
Keep constant
frequency
Change the
frequency
Keep magnetic field
constant
n =  Ho / 2

13. Nucleus Spin
quantum
number
Magnetic
moment
(m)
Gyromagnetic
ratio ()
Resonance
frequency
(MHz at a
Field of 1 T)
Relative
sensitivity
at constant
field
Natural
abundance
(%)
Quaderpole
moment, Q
1H 1/2 2.792 2.675 42.577 1.000 99.98 -
2H 1 0.857 0.411 6.536 0.009 0.0156 0.003
10B 3 1.8007 0.288 4.575 0.02 18.83 0.111
11B 3/2 2.6880 0.858 13.660 0.165 81.17 0.036
13C 1/2 0.702 0.673 10.705 0.016 1.108 -
14N 1 0.403 0.193 3.076 0.001 99.635 0.02
15N 1/2 -0.282 -0.271 4.315 0.001 0.365 -
17O 5/2 -1.8930 -0.363 5.772 0.029 0.037 -0.004
19F 1/2 2.627 2.517 40.055 0.834 100.0 -
29Si 1/2 -0.5549 -0.531 8.460 0.079 4.70 -
31P 1/2 1.131 1.083 17.235 0.066 100.0 -
Nuclear Properties of Important Nuclei -II

14. Interpretation of NMR Spectrum
NMR Spectra is analysed on the basis of following parameters
 Integration
 Chemical shift
 Coupling constant
 Rate processes
C
H3 OEt
O
4. 5 4. 0 3. 5 3. 0 2. 5 2. 0 1. 5 1. 0 0. 5
0. 0
0. 5
1. 0
1. 5
2. 0
2. 5
3. 0
3. 5
4. 0
4. 5
5. 0
5. 5
6. 0
6. 5
7. 0
7. 5
8. 0
8. 5
9. 0
9. 5

15. Integration
The process of excitation in NMR involves the flipping of the nucleus. This process of
transition and the probability of the transition is same for all the protons, irrespective of
the electronic environment. As a result, the area under the NMR resonance is
proportional to the number of hydrogens which that resonance represents.
In this way, by integrating the different NMR resonance, information regarding the
relative numbers of chemically distinct hydrogens can be found.
The integrals will appear as a line over the NMR spectrum. Integration only gives
information on the relative number of different hydrogens, not the absolute
number.
2. 5 2. 0 1. 5 1. 0 0. 5
0. 0
0. 5
1. 0
1. 5
2. 0
2. 5
3. 0
3. 5
4. 0
4. 5
5. 0
5. 5
6. 0
6. 5
7. 0
7. 5
8. 0
8. 5
9. 0
9. 5
0. 91
0. 93
0. 94
2. 08
2. 40
2. 42
2. 43
2. 45
H3C
CH3
O
4 mm
6 mm
6 mm

17. 10 56
Integration: Determination of keto – enol ratio

18. H1
electron current
Induced magnetic moment
opposing the applied
magnetic field
Chemical Shift: Shielding of a proton in a magnetic field
Basic equation of NMR is n = Ho/2 wherein resonance frequency is simply a function
of applied magnetic field and gyro magnetic ratio. If so, then all the protons in a
molecule should resonate at one place- NMR of no value to organic chemists!!!!!
What is true?
n= Ho/2
Where, Ho = strength of the applied magnetic field experienced by the nucleus.
And Ho = H1 (1   ) where H1 is the actual strength of the applied field and  is the
shielding constant.
More the electron density – more is the shielding
Less the electron density – more is the deshielding
The resonance frequency
is, to a small extent,
dependent on its
Electronic Environment
Making NMR Useful to
Structure Determination

19. The difference between the positions of absorption of reference standard
and that of a particular proton or a group of protons
Chemical Shift
0
1
2
3
4
5
Reference peak is kept at zero of the chart
What is reference ?
CH3-CH2-OH

20. Requirements for a reference standard in NMR
A good standard should meet the following requirements:
• It should be chemically inert (non-reactive).
• It should give a single sharp line.
• It should be magnetically isotropic.
• It should have unique line position.
• It should be miscible with organic solvents.
• It should be readily volatile to allow recovery of the compound.
TetraMethylSilane
Silicon is more electro-positive than carbon. Therefore,
pushes electron density towards carbon and thus to hydrogen-
making methyl protons strongly shielded.
H3C
Si
CH3
C
CH3
H
H
H

21. Units of Chemical shift
 Chemical shifts are expressed in Hz.
 Chemical shifts expressed in Hz are proportional to the applied magnetic
field HO/oscillator frequency.
 For example, In CH3CH2OH
60 MHz 100 MHz 300 MHz
CH3 60 Hz 100 Hz 300 Hz
CH2 216 Hz 360 Hz 1080 Hz
OH 300 Hz 500 Hz 1500 Hz
This can be calculated by the equation:
Frequency of X proton (Hz) in A instrument X Osc. frequency of B in Hz
Osc. frequency of A in Hz
(major difficulty in calculating chemical shift as variety of instruments)

22. Chemical shift are also expressed in d (ppm)
d = Shift in frequency from TMS (Hz) X 106
Frequency of spectrometer (Hz)
d is dimensionless and is NOT PROPORTIONAL to Ho or Osc.
frequency.
d value is same in all the different instruments
Universal scale in NMR
Higher the value of chemical shift in Hz or d  deshielded is the proton.
Lower the value chemical shift in Hz or d  shielded is the proton.
Units of Chemical shift

23. General regions of chemical shift
0
1
2
3
4
5
6
7
8
9
10
Aldehyde
Aromatic and heteroaromatic
Alkene
-Disubstituted aliphatic
-Monosubstituted aliphatic
Alkyne
-Substituted aliphatic
Aliphatic alicyclic
High field
Low field
Deshielding Shielding

24. Solvents for NMR
D3COOD 2.02, 11.53
D3CCOCD3 2.05
D3CCN 1.95
C6D6 7.20
CDCl3 7.25
CD2Cl2 5.35
D3C-SO-CD3 2.50
F3C.COOD 10-11
A satisfactory solvent
 d should be chemically inert
 d should not contain protons
 d should be non – polar and should have low – boiling point
 d should have low viscosity

25. Chemical Equivalence
 Chemically equivalent protons
H3C CH3
O
O
H3C CH3 H3CO OCH3
O
X Y Z
X, Y, and Z have one set of equivalent protons.
 Chemically non-equivalent protons
CH3CH2Cl CH3CH2OCH2CH3 CH3CH2OH
2 signals 2 signals 3 signals

26. Parameters that affect the Chemical shifts
 Electron Withdrawing Inductive Effect
 Diamagnetic anisotropic shielding and deshielding effect
 Electron donating and withdrawing mesomeric (resonance) effect

27. R CH3 0.9
R CH2 R 1.3
R3 CH 1.7
R CH2 I 3.2
R CH2 Br 3.5
R CH2 Cl 3.7
C-CH3 0.9
N-CH3 2.3
O-CH3 3.3
CH3 CR 2.1
R C CR2
CH3
1.6
O
CH3
2.3
CH3 OH 3.3
CH3 OCOCH3 3.6
CH3 OR 3.0
R2C CH R 5.3
R C C H 2.5
H
7.25
RC-H 9.7
O
Chemical shift: Electron Withdrawing Inductive effect
Electron withdrawing inductive effect is one of the parameter that
affects the chemical shift
Stronger the electron withdrawing group - more is the deshielding
R2NH
ROH
ArOH
RCO2H
2 - 4
1 - 6
6 - 8
10 - 12
Protons attached to O, N, S are resonating anywhere between 1 to 15 d. The
position depends on a) substrate b) solvent c) concentration d) temperature.
The best method to detect these protons is to re-run the spectra on addition of
drop of D2O, wherein these protons will change their position

28. Magnetic Anisotropic Effect
Carbon-Carbon double bond and triple bond
(The influence on induced magnetic moments of neighbouring bonds)
H
R1
R
H
Shielded
Region
Shielded
Region
Deshieded
Region

+
+
Deshieded
Region

Olefinic Protons at d 4.5-6.0
H
R
Shielded
Region
Shielded
Region
+
+
Deshieded
Region

Deshieded
Region

Acetylenic Protons at d 2.5-3.0
Ho
Circulation of electrons
perpendicular to Ho
Induced Magnetic
Field

29. Magnetic Anisotropic Effect
Ring Current Effect in Benzene Ring
Benzene protons at d 7.25

30. Magnetic Anisotropic Effect
Ho
Ho
Ho
(Induced by magnetic moments of neighboring bonds)

31. H
C
H
O
H
O
H
H H
CH3
CH3
H
H
H
H
H
H
H H
H
H
H
H
H
H
H
H
H
H
H OH HO H
H H
O
O O
O
OCH3
H3CO H
H3CO
H
O
O O
O
OCH3
H3CO H
H
H3CO
d 8.99
d 6.42 d 5.48
d (Ring) 8.14 - 8.64
d (CH)  4.25
d 3.53 d 3.75
d (Ring) 7.27; 6.95
d (CH2)  0.51
d  0.42 d .42
d (H outer) 9.28 d (H inner) 2.99
d  d 

32. Chemical Shift: Resonance effect
 Electron donating resonance effect increases electron density at the carbon and
in turn to hydrogen – Shielding of proton.
Electron withdrawing resonance effect decreases electron density at carbon and
in turn to hydrogen – Deshielding of proton.
OCH3
H
H
H


-H-strongly deshielded due to -I effect
-H-strongly shielded due to +M effect
OCH3
H
H
H


C
H
H
H


O
CH3
C
H
H
H


O
CH3
-H-slightly deshielded due to small -I effect
-H-slightly deshielded due to strong -M effect
R
H
H
H
5.28
5.40
6.38
3.85
5.85
6.40

33. ED ED ED EW EW EW
OCH3 - 0.43 - 0.09 - 0.37
OH - 0.5 - 0.14 - 0.40
OAc - 0.2 - 0.02 -
NH2 - 0.75 - 0.24 - 0.63
NMe2
- 0.64 - 0.10 - 0.60
Substituent Ortho Meta Para Substituent Ortho Meta Para
NO2 + 0.95 + 0.17 + 0.23
CHO + 0.58 + 0.21 + 0.27
CN + 0.27 + 0.11 + 0.30
Chemical Shift: Resonance effect

34. 2. 5 2. 0 1. 5 1. 0 0. 5
0. 0
0. 5
1. 0
1. 5
2. 0
2. 5
3. 0
3. 5
4. 0
4. 5
5. 0
5. 5
6. 0
6. 5
7. 0
7. 5
8. 0
8. 5
9. 0
9. 5
0. 91
0. 93
0. 94
2. 08
2. 40
2. 42
2. 43
2. 45
Spin-spin Coupling
• Three groups of non-equivalent hydrogens, therefore three signals
are expected.
• These signals are split into peaks due to the spin-spin interactions
of non-equivalent protons.
• Spin-spin interaction occurs between adjacent non-equivalent
protons only.
H3C
C
H2
CH3
O
Coupling constant J is always expressed in Hz
J is Independent of Operating frequency.
Multiplets are symmetric about the mid point = d
Mutually coupled protons have identical coupling constant J
J
J

35. Types of Coupling
Three types of coupling in NMR
 Geminal Coupling [1,3 coupling]:
Coupling between nuclei on the
same carbon (Two bond coupling)
Vicinal Coupling [1,4 coupling]:
Coupling between nuclei on the adjacent
carbon atom (Three bond coupling)
Long range Coupling [1,5; 1,6- coupling]
Coupling between nuclei separated by
more than three carbon atoms
(Coupling between nuclei separated by
more than three bonds)
C C
H
H
1
2
3
4
Coupling constant ‘J’ always expressed in Hz
It is independent of applied magnetic field/Operating frequency
C C
H
C
1
2
4
H
3
5
C
H
H
2
1
3

36. Rules of coupling (First Order Analysis)
Three rules govern the number and nature of multiplets in NMR
 Equivalent protons do not couple with each other.
 Maximum No. of Lines = (2na.Ia + 1) x (2nb. Ib + 1) x (2nc. Ic + 1)…….
na, nb, nc = number of neighboring non-equivalent nuclei
Ia,Ib, Ic = spin numbers of the respective nuclei.
In case of 1H, 19F and 31P nuclei, spin no. = ½.
Therefore, Maximum no. of lines = (na + 1) x (nb + 1)….
 When the multiplicity is produced by a group of equivalent nuclei with
I = ½, the intensities of the different lines are given by the coefficient of
expression (X + 1)n where n = number of interacting nuclei.
These rules are valid if n/ J > 6 (where n is a frequency difference
between coupled protons)

37. C C
HA
No adjacent proton
C C
HA HB
One adjacent non-equivalent
proton
C C
HA HB
HB
Two adjacent nonequivalent
protons
C C
HA HB
HB
HB
Three adjacent non-equivalent
protons
Structure Spin States Signals

38. Pascal’s Triangle
Relative intensities of first order multipletes
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1
n = number of equivalent nuclei Relative Intensity
0
1
2
3
4
5
6
7
8

39. Coupling of proton with neighboring nuclei

40. HO
HA
HA
HA
HA
HA
HA
HB C2 C1 HA HA C1 C2 HB
HB C2 C1 HA HA C1 C2 HB
E E2
E1
HA in the absence of HB (s)
HA in the presence of HB (d)
Line due to of HB Line due to HB
8
4
4
Jab
+1/2 J
-1/2 J
Nuclear Spin
Electron Spin
Mechanism of Spin-Spin Coupling
E – E1 = E2 - E
J Vicinal always +ve

41. Geminal Coupling
HA HB
HB
HA
E2
HO
If HB is aligned to Ho-drop in ground state and increase in exited state energy
This effect is opposite to that observed in vicinal coupling
Geminal coupling constant is usually negative
HA C HB
Low
field
High
field
Due to
of HB
Due to
of HA

42. Splitting arising from spin-spin
coupling with the protons of
the methylene group
Spin arrangements of
the methylene protons
Unperturbed
signal
HO-CH2-CH3
No. of
Total Spin Orientations
-1 1
0 2
+1 1
The splitting of the signal from the methyl protons in ethanol by spin-
spin interaction with the protons of the methylene group
+1J -1J
206 200 194
1
2
1
In ethanol, methyl appears at 1d
as a triplet with J = 6 Hz.
Line positions in 200 MHz NMR

43. The splitting of the signal from the methylene group protons in ethanol by
spin-spin interactions with the protons of the methyl group
Splitting arising from spin-spin
coupling with the protons of the
methyl group
Spin arrangements of
the methyl protons
Unperturbed
signal
No. of
Total spin Orientations
-3/2 1
-1/2 3
+1/2 3
+3/2 1
In ethanol, methylene protons appear at 3.5 d
as a quartet with J = 6 Hz
HO-CH2-CH3
709 703 697 691
700
+3/2 J -3/2 J
+1/2
-1/2
1
3 3
1
Lines in 200 MHz

44. 16
8 8
4 4 4 4
1
2
1 1
2
1 1
2
1 1
2
1
15 Hz
10Hz 10Hz
4Hz
4Hz
4Hz 4Hz 4Hz 4Hz
4Hz
Splitting due to Hb
Splitting due to Hc
Splitting
Due to Hd
Jab
Jac
Jad
1 –2 = Jad = 4 Hz
1 – 4 = Jab = 10 Hz
1 – 6 = Jab = 15 Hz
12 lines for Ha
First Order Analysis (ddt)
Hc
Hb
X
Hd
Hd
Ha

45. First Order Multiplet Analysis
Multiplets are reported starting with the largest coupling first, e.g. td J = 8.0
and 3.0 Hz implies a triplet with a J = 8.0 Hz and a doublet with J = 3.0 Hz,
which is very different from a doublet, J = 8.0 Hz and a triplet J = 3.0 Hz.
X
H
X
H
H
H
X
X
H
H
H
H
3 Hz

46. Intermediate analysis: 3 < n/ J
Second order analysis: n/ J < 3
Spin System
 If n/J ratio is large (greater than 8), the interacting nuclei are weakly coupled.
They are well separated, Designated as AM or AX.
O O
Ha
Hb
6.45
7.72
In 100 MHz
n/J = 772 – 645 = 127 Hz
J = 10 Hz
n/J = 127/10 = 12.7
 If n/J ratio is small (less than 6), the interacting nuclei are strongly coupled.
Designated as AB
S Br
Hb
Cl
Ha 5.9
6.0 In 100 MHz
n/J = 600 –590 = 10 Hz
J = 4 Hz
n/J = 10/4 = 2.5
Such a collection of set insulated from further coupling form a spin system

47. AB Multiplets: Effect of n / J ratio

48. AB Multiplet Analysis

49. Non – equivalence due to restricted rotation
19 F spectrum of BrCF2-CCl2Br
J. D. Robbert and P. M. Nair 1959
Five lines at  120 °C
Br
F
F
Cl
Br
Cl
Both F nuclei equivalent
Singlet
Br
Fb
Fa
Cl
Cl
Br
Br
Fa
Fb
Br
Cl
Cl
Both are mirror images
Both F nuclei are non equivalent
Five lines
Only one line at 25 °C
Three possible conformers

50. Non – equivalence due to restricted rotation
In case of compounds wherein methylene group is attached to the carbon
having three different groups- the two methylene protons are non – equivalent.
C
R1
R2
R3
C R
Ha
Hb
Three possible conformers
Ha
R
Hb
R3
R2
R1
Ha
R
Hb
R2
R1
R3
Ha
R
Hb
R1
R3
R2

51. AB Multiplet Analysis

52. Some approximate J values
J = 7- 9 Hz
Ortho
J = 1 - 2.5 Hz
Meta
J = very low
Para
H
H
H
H
H
H
Aromatics
H
H
H
H
H
H
C
H
C
H
J = 0 - 10 Hz Ja,a = 7 - 10 Hz Je,e = 0 - 5 Hz Ja ,e = 0 - 7 Hz
Alkanes and Cycloalkanes
H
H
H H H
H
J = 11 - 18 Hz
Trans
J = 5 - 14 Hz
Cis
J = 8 - 11 Hz
H
H
H
H
J = 0 - 3 Hz
SP2
Geminal
J = 11 - 18 Hz
SP3
Geminal
Alkenes

53. Factors affecting Vicinal Coupling Constant (3J)
The magnitude of 3J (sign is always positive) depends in essence upon four factors
 The dihedral angle , between the C-H bonds
under consideration (a).
 The C,C bond length, Rmn (b).
 The H-C-C valence angles,  and ’ (c)
 The electronegativity of the substituent
R on the H-C-C-H
H
H

a
H H
Rm,n
b
H H
 '
c
H H
R
d

54. Karplus Correlation
Relationship between dihedral angle () and coupling constant for vicinal protons
Axial - axial
Axial - equatorial
Equatorial - equatorial
Dihedral Angle Calculated J (Hz) Observed J (Hz)
180°
60°
60°
9
1.8
1.8
8 -14
1 - 7
1 - 7

55. Rate Processes
NMR of CH3CH2OH ( with trace of acid/base impurity)
CH3-CH2-O-H
H+
CH3-CH2-O
H
H
CH3-CH2-O
H
H
H+
H+
NMR of pure ethanol

56. Effect of High Oscillator Frequency
Chemical shift in Hz is proportional to the oscillator frequency.
Coupling constant J in Hz is not proportional to the oscillator frequency.
As a result, NMR spectra are more resolved at high operating frequency.
For example:The NMR of compound BrCH2CH2CH2 shows:
d 3.70 (t, J = 7 Hz), 3.55 (t, J = 7 Hz), 2.27 (quin, J = 7 Hz)
As n/J ratio increases - NMR is more resolved
Interpreted by first order analysis
3.70 = 1110 Hz
1 2 1
1117
1110
1103
1 2 1
1072
1065
1058
3.55 = 1065 Hz
1117
1110
1103 1072
1065
1058
300 MHz instrument
3.70 = 222 Hz
1 2 1
229
222
215
1 2 1
220
213
206
3.55 = 213 Hz
229
222
220215
213
206
60 MHz instument
n / J = 9/7 =1.3
n / J = 45/7 =6.5

57. AMX Spin System

58. ADVANCES IN MRI
Magnetic Resonance Imaging (MRI) has reached a
high level of maturity and has established itself as the
diagnostic modality of choice in almost all neurological
system disorders, joint diseases, Mediastinal and
heart pathologies, work-up of abdominal and pelvic
malignancies and evaluation of vascular system of the
body.