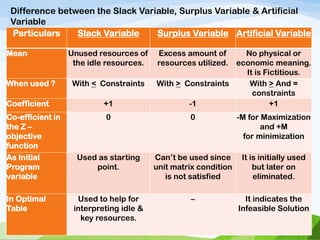
The document introduces slack variables, surplus variables, and artificial variables. Slack variables are added to ≤ constraints to convert them to equations. Surplus variables are subtracted from ≥ constraints. Artificial variables are added to = and ≥ constraints to satisfy non-negativity conditions. The document provides examples of converting linear programming problems to standard form using these variable types.

1. SlaCk variable,
surplus varIable
& Artificial
Variabal

2. Content:
1. Introduction of Simplex Method
2. Concept of Slack Variable, Surplus Variable & Artificial
variable
3. Difference between the Slack Variable, Surplus Variable &
Artificial Variable
4. Solved Examples

3. Simplex Method/ Simplex Techniques/ Simplex
algorithm
Introduction:
• Simplex method was developed by Prof. George. B. Dantize
and American Mathematician in 1947 which was made
available in 1951.
• This method is an iterative (Step by Step) procedure in
which we proceed in systematic steps from an initial basic
feasible solution to other Basic feasible solution and finally
in a finite number of steps, to an optimal B.F. solution, in
such a way that the value of the objective function at each
step(intenration) is better than at the preceding step.

4. Concept of Slack Variable, Surplus Variable & Artificial variable
When decision variables are more than 2, we always use
simplex method.
Slack Variable:
Variable added to a ≤ constraint to convert it to an equation (=).
• Slack variable represents unused resources.
• A slack variable contributes nothing to the objective function value.
j = 1.
For determination of feasible solution, each inequality in the
constraint equation be written as equality for the purpose of drawing
straight line.
Eg. 2X1 + 3X2 + S3 = 60
Inequality is converted in to equality. Thus slack variable is used
to convert less than

5. THE SIMPLEX METHOD: MAXIMIZATION(Adding Slack Variable)
• Suppose we want to find the maximum value of where and subject
to the following constraints.
- X1 + X2 ≤ 11
X1 + X2 ≤ 27
2X1 + 5X2 ≤ 90
• Since the left-hand side of each inequality is less than or equal to
the right-hand side, there must exist nonnegative numbers S1, S2 &
S3 that can be added to the left side of each equation to produce
the following system of linear equations.
- X1 + X2 + S1 = 11
X1 + X2 + S2 = 27
2X1 + 5X2 + S3 = 90
• The numbers S1, S2 & S3 are called slack variables because they
take up the “slack” in each inequality.

6. Surplus Variable:
Variable subtracted form a ≥ constraint requirement level.
• A surplus variable represents the amount by which solution
values exceed a resource. These variables are also called
„Negative Slack Variables‟ .
• Surplus variables like slack variables carry a zero
coefficient in the objective function. it is added to greater
than or equal to (>) type constraints in order to get an
equality constraint.

7. Continue…………..
A variable which is subtracted from the left hand side of a
greater than or equal to constraint in to equality is called surplus
variable.
a11X1 + a12X2 + …………. a1nXn - Xn+1 = b1
Example:
2X1 + 3X2 ≥ 60
2X1 + 3X2 ≥ 60 + X3
2X1 + 3X2 - X3 = 60
X3 is Surplus variable

8. Artificial Variable:
• Artificial variables are added to those constraints with equality (=)
and greater than or equal to ( > ) sign.
• A fictitious variable included in the case of inequality of ≥ type and
equality(=), to satisfy the non negativity condition of a basic feasible
solution.
• Introduce an Artificial Variable in each = constraint.
• For each artificial variable A, add – A to the objective function.
• Use the same constant M for all artificial variables.

9. Continue……………
Objective function
Max Z = 3X1 - 2X2 + X3
Subject to
X1 - 2X2 + X3 ≥ 5
- X1 - 3X2 + 4 X3 ≤ - 10
2X1 + 4X2 + 5 X3 ≤ 20
3X1 - X2 - X3 = -15
Non negative constraint
X1, X2, X3 ≥ 0

10. • Introduce a surplus variable and an artificial variable for the first
constraint:
X1 - 2X2 + X3 ≥ 5
X1 - 2X2 + X3 - S1 + A1 = 5
• Notice that the second constraint has a negative number on the
right hand side. To make that number positive multiply both sides
by -1 and reverse the direction of the inequality:
X1 + 3X2 − 4 X3 ≥ 10
• The fourth constraint has a negative number on the right hand side
so multiply both sides of this equation by -1 to change the sign of - 5
to + 15.
- 3X1 + X2 + X3 = 15

11. • Do the same procedure for the Second constraint: ≥
X1 + 3X2 − 4 X3 − S2 + A2 = 10
• Introduce surplus variable for les than or equal to third constraint:
2X1 + 4X2 + 5 X3+ S3 = 20
• Introduce the third artificial variable for the equation constraint:
- 3X1 + X2 + X3 + A3= 15
• For each of the three artificial variables, we will add – A to the
Objective function.
Z = 3X1 - 2X2 + X3 - A1 - A2 - A3

12. Continue……………..
Final result, Modified problem is,
Max Z = 3X1 - 2X2 + X3 + 0S1 + 0S2 + 0S3 - MA1 - MA2 - MA3
Subject to the constraints:
X1 - 2X2 + X3 - S1 + A1 = 5
X1 + 3X2 − 4 X3 − S2 + A2 = 10
2X1 + 4X2 + 5 X3+ S3 = 20
- 3X1 + X2 + X3 + A3 = 15
X1, X2, X3 ≥ 0

13. Difference between the Slack Variable, Surplus Variable & Artificial
Variable
Particulars Slack Variable Surplus Variable Artificial Variable
Mean Unused resources of
the idle resources.
Excess amount of
resources utilized.
No physical or
economic meaning.
It is Fictitious.
When used ? With < Constraints With > Constraints With > And =
constraints
Coefficient +1 -1 +1
Co-efficient in
the Z –
objective
function
0 0 -M for Maximization
and +M
for minimization
As Initial
Program
variable
Used as starting
point.
Can‟t be used since
unit matrix condition
is not satisfied
It is initially used
but later on
eliminated.
In Optimal
Table
Used to help for
interpreting idle &
key resources.
– It indicates the
Infeasible Solution

14. Examples:
1. Write the Standard form of the following LPP.
Max Z = 2X1 - 4X2 - 5X3 − 6X4
Subject to,
X1 + 2X2 - X3 + X4 ≤ 2
- X1 + 2X2 + 3X3 + 4X4 ≤ 1
X1, X2, X3 & X4 ≥ 0
Determine the maximum number of possible
basic solutions of Standard form.

15. Continue………………
Solution:
Max Z = 2X1 - 4X2 - 5X3 − 6X4 + 0S1 + 0𝑆2
Subject to,
X1 + 4X2 - 2X3 + 8X4+ S1 = 2
- X1 + 2X2 + 3X3 + 4X4+ S2 = 1
X1, X2, X3 & X4 ≥ 0

16. 2. Convert the following LPP to standard form.
Determine X1, & X2 ≥ 0 so as to,
Max Z = 5X1 + 3X2
Subject to,
2X1 + 5X2 ≤ 2
2X1 + 3X2 ≥ 5
X1 & X2 ≥ 0

17. Continue…………
Solution: Add a Slack, Surplus & Artificial Variable
Max Z = 5X1 + 3X2 + 0S1+ 0S2 - MA
Subject to,
2X1 + 5X2 + S1= 2
2X1 + 3X2 − S2 + A1 = 5
X1, X2, S1 & S2 ≥ 0
Where,
S1 is Slack Variable,
S2 is Surplus variable & A1 is Artificial Variable

18. 3. Convert the following LPP to standard form.
Determine X1, & X2 ≥ 0 so as to,
Max Z = 4X1 + X2
Subject to,
X1 + 2X2 ≤ 3
4X1 + 3X2 ≥ 6
3X1 + X2 = 3
X1 & X2 ≥ 0

19. Continue………….
Solution: Firstly we add a Slack, Surplus & Artificial Variable
Max Z = 5X1 + 3X2 + 0S1+ 0S2 - MA1 - MA2
Subject to,
X1 + 2X2 + S1 = 3
4X1 + 3X2 − S2 + A1 = 6
3X1 + X2 + A2 = 3
X1, X2, S1, S2 , A1 & A2 ≥ 0
Where, S1 is Slack Variable,
S2 is Surplus variable
A1 & A2 is Artificial Variable