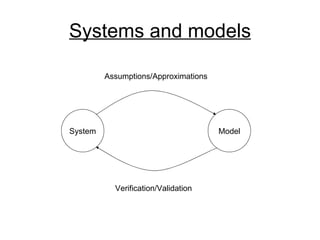
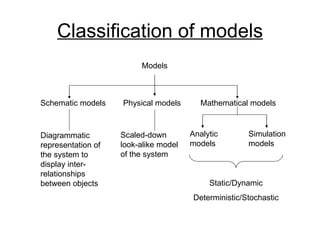
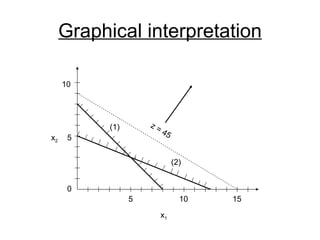
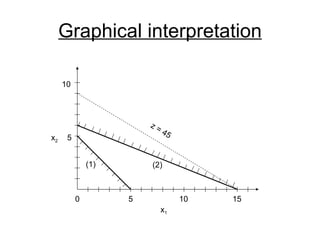
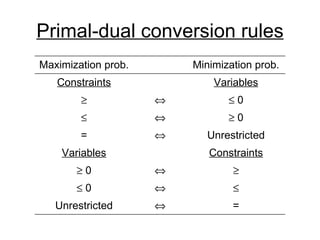
The document provides an overview of operations research (OR) and linear programming (LP). Some key points: - OR deals with allocating scarce resources effectively and was introduced during WWII to help with military operations. - LP is a branch of OR that uses mathematical modeling to determine the optimal allocation of resources. It involves modeling a system as variables and constraints in order to find the best solution. 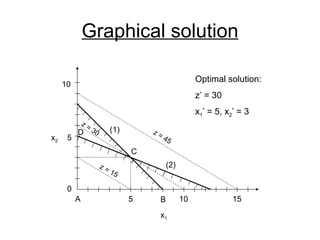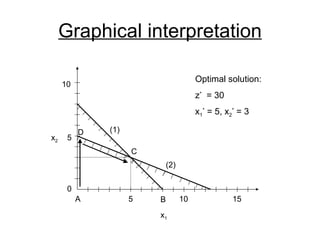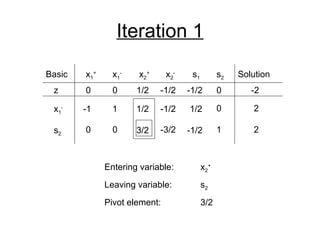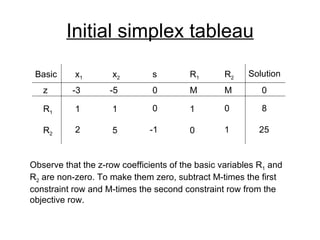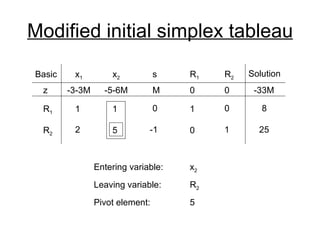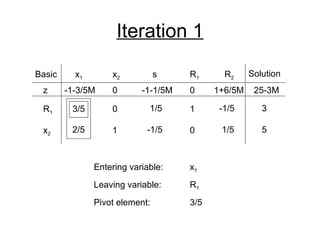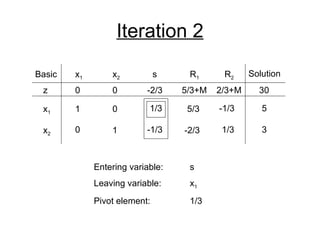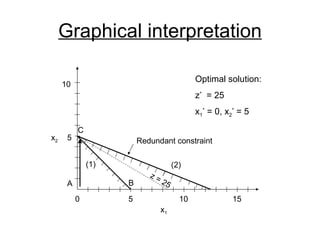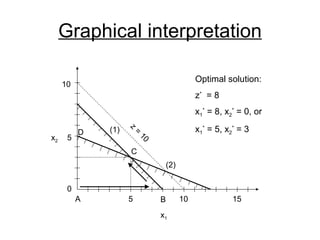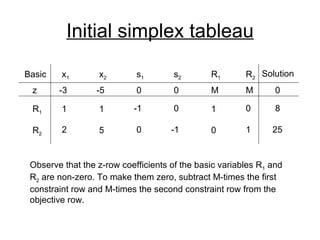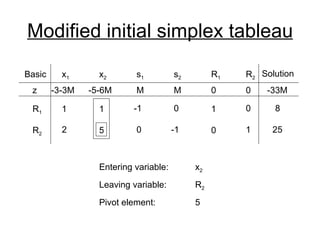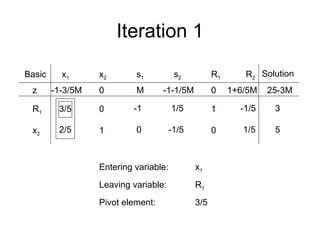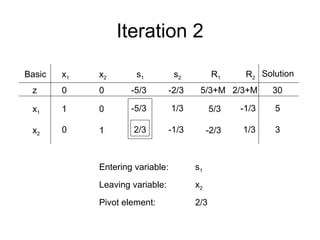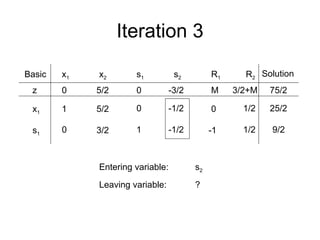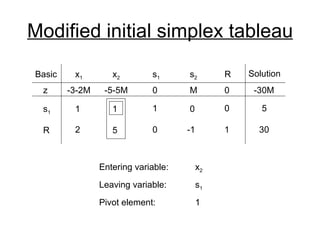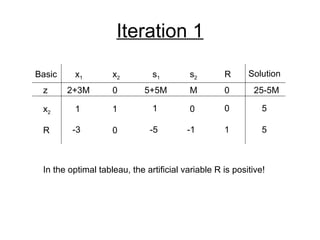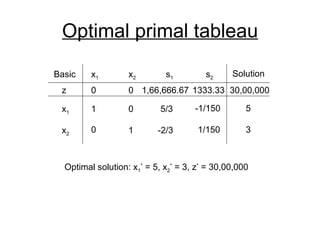- The simplex method is commonly used to solve LP problems by systematically moving from one basic feasible solution to another with an improved objective value until an optimal solution is found.

1. Operations Research Linear Programming

2. Operations Research (OR) Branch of mathematics that deals with the allocation of scarce resources to various activities in the most effective manner Objective is to search for the best (optimal) solution(s) from among a number of alternative solutions Introduced during World War II (WW II)

3. Operations Research (OR) Scientists were asked to do research on (military) operations during WW II Success of OR led to the spread of its large-scale applications in business, industry and government Spread of OR was facilitated by the rapid growth in computational power

4. Systems and models System Collection of interrelated objects Model Abstraction of reality Representation of a system to study the behaviour of the system

5. Systems and models System Model Assumptions/Approximations Verification/Validation

6. Classification of models Models Schematic models Physical models Mathematical models Analytic models Simulation models Static/Dynamic Deterministic/Stochastic Diagrammatic representation of the system to display inter-relationships between objects Scaled-down look-alike model of the system

7. Academics or extra-curricular? Suppose you consider academics and extra-curricular activities are the two most important aspects that have direct bearings on your prospects for placements. You estimate the ratio of the impact of devoting 1 hour to academics to the impact of devoting 1 hour to extra-curricular activities on your placement prospects to be 3:5. You decide not to spend more than 8 hours daily for these two activities. Moreover, you estimate that 1 hour of academics and 1 hour of extra-curricular activities burn, on an average, 100 and 250 calories, respectively, and you cannot afford to burn more than 1250 calories for these two activities based on your average daily calorie intake. Q . How many hours should you devote to academics and extra-curricular activities daily?

8. Academics or extra-curricular? Decision variables: x 1 : No. of hours devoted to academics daily x 2 : No. of hours devoted to extra-curricular activities daily Objective function: Maximize the impact on placement prospects Max z = 3x 1 + 5x 2 Constraints: x 1 + x 2 <= 8 (1) 100x 1 + 250x 2 <= 1250 or 2x 1 + 5x 2 <= 25 (2) Non-negativity restrictions: x 1 , x 2 >= 0

9. Graphical solution 5 5 10 10 15 0 A B C D (1) (2) z = 45 z = 30 z = 15 Optimal solution: z * = 30 x 1 * = 5, x 2 * = 3 x 1 x 2

10. Assumptions in LP Proportionality Additivity Divisibility Certainty

11. Simplex algorithm Developed by Dantzig in 1947 Convert the LP to standard form: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 + s 1 = 8 2x 1 + 5x 2 + s 2 = 25 x 1 , x 2 , s 1 , s 2 >= 0 s 1 and s 2 are slack variables

12. Basic and non-basic variables If there are n variables and m linear equations in the standard form of an LP (n>m), we can set (n – m) non-basic variables equal to zero and solve for the remaining m basic variables that satisfy the set of linear equations (provided it has a unique solution) A basic solution that satisfies the non-negativity restrictions is called a basic feasible solution

13. Steps in simplex algorithm Determine a starting basic feasible solution. Call it the current basic feasible solution If the current basic feasible solution is optimal, stop. Otherwise, determine a new basic feasible solution that has an improved z-value Calling the new basic feasible solution as the current basic feasible solution, go back to step 2

14. Initial simplex tableau z s 2 s 1 x 1 x 2 s 1 s 2 Basic Solution -3 -5 0 0 0 0 1 1 1 2 5 1 0 8 25 Entering variable: x 2 Leaving variable: s 2 Pivot element: 5

15. Iteration 1 z x 2 s 1 x 1 x 2 s 1 s 2 Basic Solution -1 0 0 1 -1/5 0 3/5 0 1 2/5 1 1/5 25 3 5 Entering variable: x 1 Leaving variable: s 1 Pivot element: 3/5

16. Iteration 2 z x 2 x 1 x 1 x 2 s 1 s 2 Basic Solution 0 0 5/3 2/3 -1/3 -2/3 1 0 5/3 0 1 1/3 30 5 3 Optimal solution: x 1 * = 5, x 2 * = 3, z * = 30 Upper bound on the no. of iterations = Maximum no. of basic solutions = n C m

17. Optimality and feasibility Optimality condition The entering variable in a maximization (minimization) problem is the non-basic variable having the most negative (positive) coefficient in the z-row. Ties are broken arbitrarily. The optimum is reached at the iteration where all the z-row coefficients of the non-basic variables are non-negative (non-positive) Feasibility condition For both the maximization and minimization problems, the leaving variable is the basic variable associated with the smallest non-negative ratio. Ties are broken arbitrarily

18. Simplex method Determine a starting basic feasible solution Select an entering variable using the optimality condition. Stop if there is no entering variable Select a leaving variable using the feasibility condition Determine the new basic feasible solution by using the appropriate Gauss-Jordan computations. Go back to step 2

19. Graphical interpretation 5 5 10 10 15 0 A B C D (1) (2) Optimal solution: z * = 30 x 1 * = 5, x 2 * = 3 x 1 x 2

20. Example: Company X Company X produces two products - A and B - with two raw materials, V and W the maximum availabilities of which are 7000 and 6000 units, respectively. To produce one unit of A(B), 1(2) unit(s) of V and 3(1) units of W are required. If the contributions per unit of A and B are Rs. 2 and Rs. 3, respectively, determine how many units of A and B should Company X produce in order to maximize the total contribution. Solution: A - 1000 units and B - 3000 units

21. Treating free variables Min z = x 1 – x 2 Subject to -2x 1 + x 2 <= 4 (1) - x 1 + 2x 2 <= 4 (2) x 1 , x 2 free x 1 x 2 -2 -4 2 4 (-4/3, 4/3) z = -8/3 (1) (2) 0

22. Conversion to standard LP Write x 1 = x 1 + - x 1 - and x 2 = x 2 + - x 2 - Min z = x 1 + - x 1 - - x 2 + + x 2 - Subject to - 2x 1 + + 2x 1 - + x 2 + - x 2 - + s 1 = 4 - x 1 + + x 1 - + 2x 2 + - 2x 2 - + s 2 = 4 x 1 + , x 1 - , x 2 + , x 2 - , s 1 , s 2 >= 0

23. Initial simplex tableau z s 2 s 1 x 1 - x 2 - s 1 s 2 Basic Solution 1 1 0 0 0 0 2 1 1 1 2 1 0 4 4 Entering variable: x 1 - Leaving variable: s 1 Pivot element: 2 x 1 + x 2 + -1 -1 -2 -1 -1 -2

24. Iteration 1 z s 2 x 1 - x 1 - x 2 - s 1 s 2 Basic Solution 0 1/2 -1/2 0 0 -1/2 1 1/2 1/2 0 3/2 1 -2 2 2 Entering variable: x 2 + Leaving variable: s 2 Pivot element: 3/2 x 1 + x 2 + 0 -1/2 -1 -1/2 0 -3/2

25. Iteration 2 z x 2 + x 1 - x 1 - x 2 - s 1 s 2 Basic Solution 0 0 -1/3 -1/3 -1/3 1 0 2/3 0 1 2/3 -8/3 4/3 Optimal solution: x 1 - = 4/3, x 2 + = 4/3, z* = -8/3 or x 1 * = -4/3, x 2 * = 4/3, z* = -8/3 x 1 + x 2 + 0 0 -1 0 0 -1 4/3 -1/3

26. Treating “=” and “>=” constraints Suppose in the “academics or extra-curricular?” problem, you decide to devote exactly 8 hours (no less, no more) daily to these two activities. Also, you would like to burn at least 1250 calories for these two activities. Other data remaining the same, how many hours would you now devote to academics and extra-curricular activities daily? Modified formulation: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 = 8 (1) 2x 1 + 5x 2 >= 25 (2) x 1 , x 2 >= 0 Standard form: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 = 8 2x 1 + 5x 2 - s = 25 x 1 , x 2 , s >= 0 s is a surplus variable

27. M-method Max z = 3x 1 + 5x 2 – MR 1 – MR 2 Subject to x 1 + x 2 + R 1 = 8 2x 1 + 5x 2 - s + R 2 = 25 x 1 , x 2 , s, R 1 , R 2 >= 0 R 1 , R 2 are called artificial variables M is a large number

28. Initial simplex tableau z R 2 R 1 x 1 x 2 s R 1 Basic Solution -3 -5 0 M 0 0 1 1 1 2 5 1 0 8 25 R 2 M 0 -1 Observe that the z-row coefficients of the basic variables R 1 and R 2 are non-zero. To make them zero, subtract M-times the first constraint row and M-times the second constraint row from the objective row.

29. Modified initial simplex tableau z R 2 R 1 x 1 x 2 s R 1 Basic Solution -3-3M -5-6M M 0 0 0 1 1 1 2 5 1 -33M 8 25 R 2 0 0 -1 Entering variable: x 2 Leaving variable: R 2 Pivot element: 5

30. Iteration 1 z x 2 R 1 x 1 x 2 s R 1 Basic Solution -1-3/5M 0 -1-1/5M 0 -1/5 0 3/5 0 1 2/5 1 1/5 25-3M 3 5 R 2 1+6/5M 1/5 -1/5 Entering variable: x 1 Leaving variable: R 1 Pivot element: 3/5

31. Iteration 2 z x 2 x 1 x 1 x 2 s R 1 Basic Solution 0 0 -2/3 5/3+M -1/3 -2/3 1 0 5/3 0 1 1/3 30 5 3 R 2 2/3+M 1/3 -1/3 Entering variable: s Leaving variable: x 1 Pivot element: 1/3

32. Iteration 3 z x 2 s x 1 x 2 s R 1 Basic Solution 2 0 0 5+M -1 1 3 0 5 1 1 0 40 15 8 R 2 M 1 0 Optimal solution: x 1 * = 0, x 2 * = 8, z * = 40

33. Special cases in simplex Degeneracy Alternative optima Unbounded solutions Infeasible solutions

34. Degeneracy Suppose in the “academics or extra-curricular?” problem, you decide not to devote more than 5 hours daily to these two activities. Other data remaining the same, how many hours would you now devote to academics and extra-curricular activities daily? Modified formulation: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 <= 5 (1) 2x 1 + 5x 2 <= 25 (2) x 1 , x 2 >= 0 Standard form: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 + s 1 = 5 2x 1 + 5x 2 + s 2 = 25 x 1 , x 2 , s 1 , s 2 >= 0

35. Initial simplex tableau z s 2 s 1 x 1 x 2 s 1 s 2 Basic Solution -3 -5 0 0 0 0 1 1 1 2 5 1 0 5 25 Entering variable: x 2 Leaving variable: s 2 Pivot element: 5

36. Iteration 1 z x 2 s 1 x 1 x 2 s 1 s 2 Basic Solution -1 0 0 1 -1/5 0 3/5 0 1 2/5 1 1/5 25 0 5 Entering variable: x 1 Leaving variable: s 1 Pivot element: 3/5

37. Iteration 2 z x 2 x 1 x 1 x 2 s 1 s 2 Basic Solution 0 0 5/3 2/3 -1/3 -2/3 1 0 5/3 0 1 1/3 25 0 5 Optimal solution: x 1 * = 0, x 2 * = 5, z * = 25

38. Graphical interpretation 5 5 10 10 15 0 A B C (1) (2) Optimal solution: z * = 25 x 1 * = 0, x 2 * = 5 x 1 x 2 z = 25 Redundant constraint

39. Alternative optima Suppose in the “academics or extra-curricular?” problem, you estimate that the effect of 1 hour of academics and the effect of 1 hour of extra-curricular activities on your placement prospects are the same. Other data remaining the same, how many hours would you now devote to academics and extra-curricular activities daily? Modified formulation: Max z = x 1 + x 2 Subject to x 1 + x 2 <= 8 (1) 2x 1 + 5x 2 <= 25 (2) x 1 , x 2 >= 0 Standard form: Max z = x 1 + x 2 Subject to x 1 + x 2 + s 1 = 8 2x 1 + 5x 2 + s 2 = 25 x 1 , x 2 , s 1 , s 2 >= 0

40. Initial simplex tableau z s 2 s 1 x 1 x 2 s 1 s 2 Basic Solution -1 -1 0 0 0 0 1 1 1 2 5 1 0 8 25 Entering variable: x 1 Leaving variable: s 1 Pivot element: 1

41. Iteration 1 z s 2 x 1 x 1 x 2 s 1 s 2 Basic Solution 0 0 1 0 0 -2 1 1 1 0 3 1 8 8 9 Entering variable: x 2 Leaving variable: s 2 Pivot element: 3

42. Iteration 2 z x 2 x 1 x 1 x 2 s 1 s 2 Basic Solution 0 0 1 0 -1/3 -2/3 1 0 5/3 0 1 1/3 8 5 3 Optimal solution: x 1 * = 5, x 2 * = 3, z * = 8

43. Graphical interpretation 5 5 10 10 15 0 A B C D (1) (2) Optimal solution: z * = 8 x 1 * = 8, x 2 * = 0, or x 1 * = 5, x 2 * = 3 x 1 x 2 z = 10

44. Unbounded solutions Suppose in the “academics or extra-curricular?” problem, you decide to devote at least 8 hours daily to these two activities. Also, you would like to burn at least 1250 calories for these two activities. Other data remaining the same, how many hours would you now devote to academics and extra-curricular activities daily? Modified formulation: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 >= 8 (1) 2x 1 + 5x 2 >= 25 (2) x 1 , x 2 >= 0 Standard form: Max z = 3x 1 + 5x 2 - MR 1 - MR 2 Subject to x 1 + x 2 - s 1 + R 1 = 8 2x 1 + 5x 2 - s 2 + R 2 = 25 x 1 , x 2 , s 1 , s 2 , R 1 , R 2 >= 0

45. Initial simplex tableau z R 2 R 1 x 1 x 2 s 1 R 1 Basic Solution -3 -5 0 M 0 0 1 1 1 2 5 1 0 8 25 R 2 M 0 -1 Observe that the z-row coefficients of the basic variables R 1 and R 2 are non-zero. To make them zero, subtract M-times the first constraint row and M-times the second constraint row from the objective row. s 2 0 -1 0

46. Modified initial simplex tableau z R 2 R 1 x 1 x 2 s 1 R 1 Basic Solution -3-3M -5-6M M 0 0 0 1 1 1 2 5 1 -33M 8 25 R 2 0 0 -1 s 2 M -1 0 Entering variable: x 2 Leaving variable: R 2 Pivot element: 5

47. Iteration 1 z x 2 R 1 x 1 x 2 s 1 R 1 Basic -1-3/5M 0 M 0 -1/5 0 3/5 0 1 2/5 1 1/5 25-3M 3 5 R 2 1+6/5M 1/5 -1/5 s 2 -1-1/5M -1 0 Entering variable: x 1 Leaving variable: R 1 Pivot element: 3/5 Solution

48. Iteration 2 z x 2 x 1 x 1 x 2 s 1 R 1 Basic 0 0 -5/3 5/3+M -1/3 -2/3 1 0 5/3 0 1 1/3 30 5 3 R 2 2/3+M 1/3 -1/3 s 2 -2/3 -5/3 2/3 Entering variable: s 1 Leaving variable: x 2 Pivot element: 2/3 Solution

49. Iteration 3 z s 1 x 1 x 1 x 2 s 1 R 1 Basic 0 5/2 0 M 1/2 -1 1 5/2 0 0 3/2 1/2 75/2 25/2 9/2 R 2 3/2+M -1/2 -1/2 s 2 -3/2 0 1 Solution Entering variable: s 2 Leaving variable: ?

50. Graphical interpretation 5 5 10 10 15 0 (1) (2) x 1 x 2 z = 45

51. Infeasible solutions Suppose in the “academics or extra-curricular?” problem, you decide to devote at most 5 hours daily to these two activities. Also, you would like to burn at least 1500 calories for these two activities. Other data remaining the same, how many hours would you now devote to academics and extra-curricular activities daily? Modified formulation: Max z = 3x 1 + 5x 2 Subject to x 1 + x 2 <= 5 (1) 2x 1 + 5x 2 >= 30 (2) x 1 , x 2 >= 0 Standard form: Max z = 3x 1 + 5x 2 - MR Subject to x 1 + x 2 + s 1 = 5 2x 1 + 5x 2 - s 2 + R = 30 x 1 , x 2 , s 1 , s 2 , R >= 0

52. Initial simplex tableau z R s 1 x 1 x 2 s 1 s 2 Basic Solution -3 -5 0 0 0 0 1 1 0 2 5 1 0 5 30 R M 1 -1 Observe that the z-row coefficient of the basic variable R is non-zero. To make it zero, subtract M-times the second constraint row from the objective row.

53. Modified initial simplex tableau z R s 1 x 1 x 2 s 1 s 2 Basic Solution -3-2M -5-5M 0 M 0 0 1 1 0 2 5 1 -30M 5 30 R 0 1 -1 Entering variable: x 2 Leaving variable: s 1 Pivot element: 1

54. Iteration 1 z R x 2 x 1 x 2 s 1 s 2 Basic Solution 2+3M 0 5+5M M 0 -5 1 1 0 -3 0 1 25-5M 5 5 R 0 1 -1 In the optimal tableau, the artificial variable R is positive!

55. Graphical interpretation 5 5 10 10 15 0 (1) (2) x 1 x 2 z = 45

56. Duality Consider the “academics or extra-curricular?” problem in modified form: Primal problem Max z = 3,00,000x 1 + 5,00,000x 2 Subject to x 1 + x 2 <= 8 100x 1 + 250x 2 <= 1250 x 1 , x 2 >= 0

57. Resources and their worth Resources Time: Maximum availability 8 hours Energy: Maximum availability 1250 calories Worth of resources y 1 : Unit worth of resource ‘Time’ y 2 : Unit worth of resource ‘Energy’

58. Dual formulation Dual problem Min w = 8y 1 + 1250y 2 Subject to y 1 + 100y 2 >= 3,00,000 y 1 + 250y 2 >= 5,00,000 y 1 , y 2 >= 0

59. Primal-dual conversion rules Maximization prob. Minimization prob. Constraints Variables    0    0 =  Unrestricted Variables Constraints  0    0   Unrestricted  =

60. Academics or extra-curricular? Primal problem expressed in standard form: Max z = 3,00,000x 1 + 5,00,000x 2 Subject to x 1 + x 2 + s 1 = 8 100x 1 + 250x 2 + s 2 = 1250 x 1 , x 2 , s 1 , s 2 >= 0

61. Optimal primal tableau z x 2 x 1 x 1 x 2 s 1 s 2 Basic Solution 0 0 1,66,666.67 1333.33 -1/150 -2/3 1 0 5/3 0 1 1/150 30,00,000 5 3 Optimal solution: x 1 * = 5, x 2 * = 3, z * = 30,00,000

62. Example: Company X z x 1 x 2 x 1 x 2 s 1 s 2 Basic Solution 0 0 1.4 0.20 -1/5 -1/5 0 1 3/5 1 0 2/5 11,000 3000 1000 Optimal solution: x 1 * = 1000, x 2 * = 3000, z * = 11,000 Optimal primal tableau