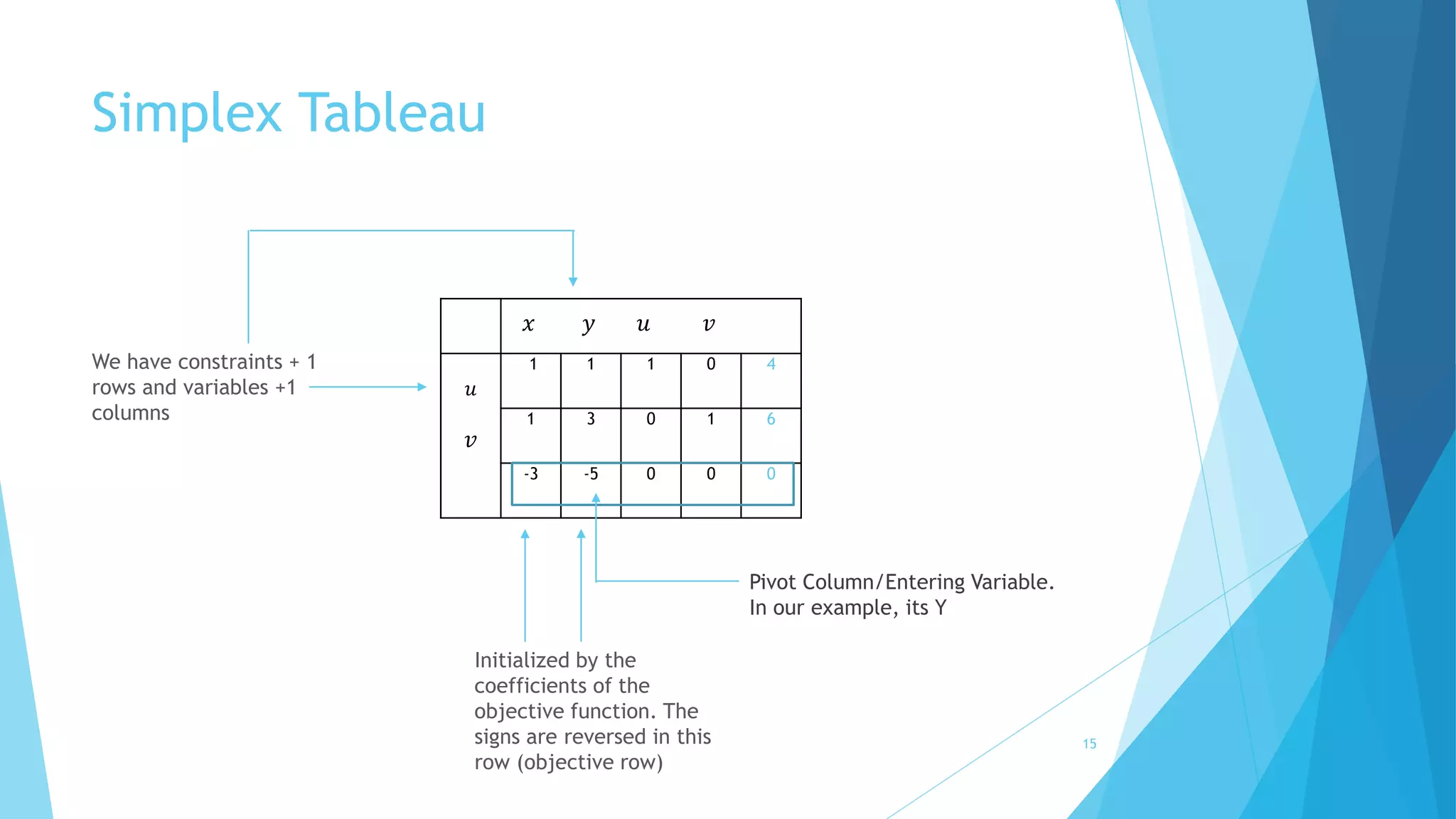
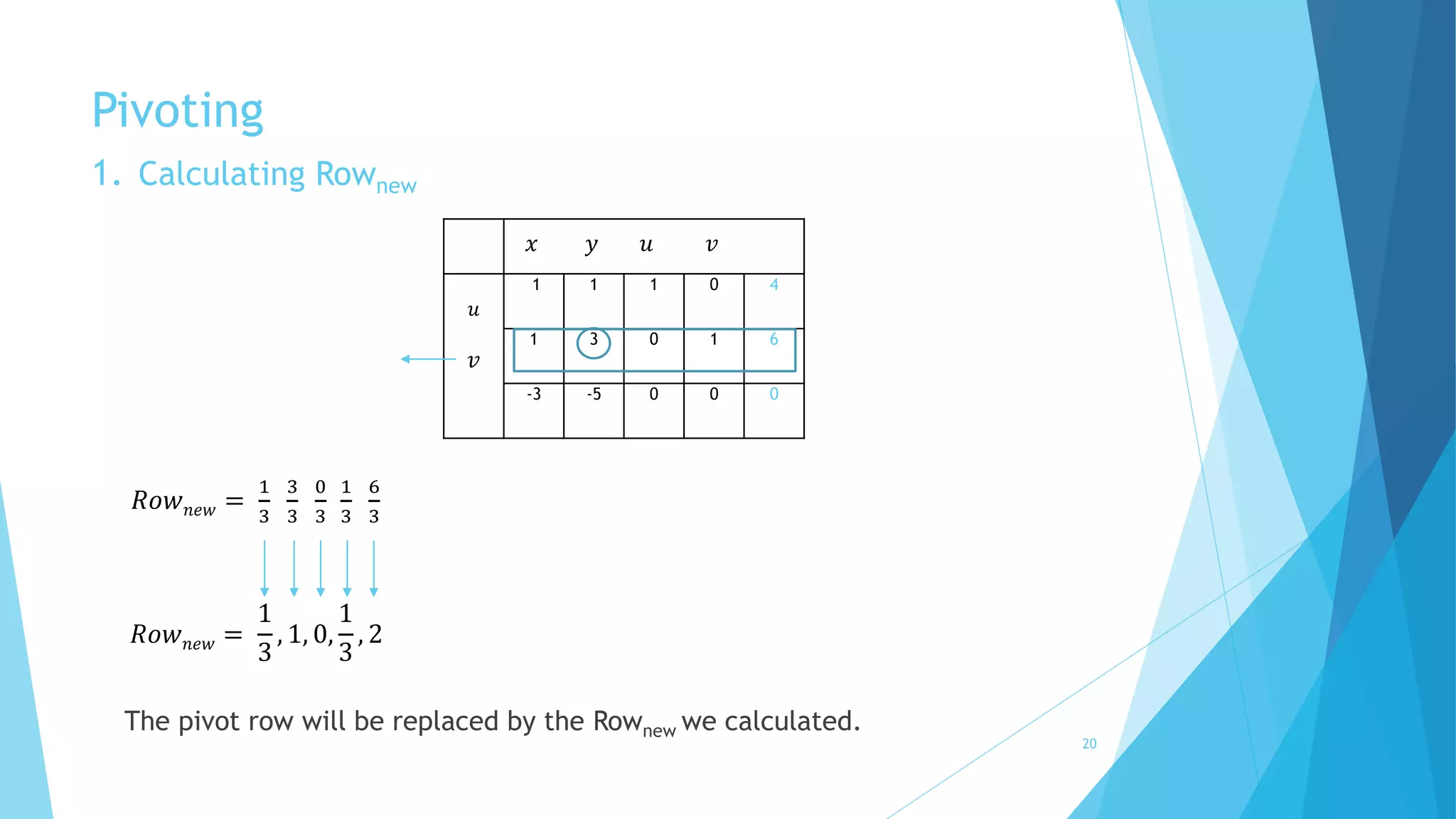
The document provides an overview of the simplex algorithm for solving linear programming problems. It begins with an introduction and defines the standard format for representing linear programs. It then describes the key steps of the simplex algorithm, including setting up the initial simplex tableau, choosing the pivot column and pivot row, and pivoting to move to the next basic feasible solution. It notes that the algorithm terminates when an optimal solution is reached where all entries in the objective row are non-negative. The document also briefly discusses variants like the ellipsoid method and cycling issues addressed by Bland's rule.

1. Simplex Algorithm
Linear Programming
Khwaja - Sarwan - Aizaz - Ghaffar
1

2. Overview
 Introduction
 Simplex Algorithm/Method
 Steps For Simplex Algorithm
1. Standardization
2. Simplex Tableau
3. Pivot Column
4. Theta Ratio and Pivot Row
5. Pivoting
1. Calculate Rownew
2. Calculate Row – C.Rownew
 Cycling – Bland’s Rule
 Software Simulation
 Efficiency
 Other Variants of the Algorithm
 Summary of Algorithm
 Acknowledgement 2

3. Simplex Method
 Last week, we covered on using the graphical approach in deriving solutions
for LP problem
 Question:
 Can we solve all LP problems using graphical approach ?
3

4. Answer is “NO”
 Why?
 Consider the following scenario:
15퐶 = 3003) of basic
For 10 equations with 15 variables there exists a huge number ( 10
feasible solutions. In such a case, inspection of all the solutions one-by-one is not
practically feasible.
 It is extremely difficult to use a graphical approach to find its
maximized/minimized solution.
 Thus, we need another systematic approach to solve an LP problem -
known as Simplex Method/Algorithm.
4

5. Simplex Method
 The most popular method used for the solution of Linear Programming Problems
(LPP) is the simplex method.
 The journal Computing in Science and Engineering listed it as one of the top 10
algorithms of the twentieth century.
 An American Mathematical Scientist, George Bernard Dantzig is known for his
development of the simplex algorithm. That’s why we also name it Dantzig’s
Algorithm.
 The algorithm is derived from the geometrical concept of Simplex
(plural simplexes or simplices).
 Simplex Algorithm can solve an equation for many variables (dimensions).
5

6. Steps for Simplex Algorithm
1. Standardization
We need to convert our equation into a standard format first.
We refer standard format here as.
 It must be a maximization problem.
 All constraints are in a form of “equation”
 i.e. not equation of ≥ or ≤
 All variables must be required to be nonnegative
6

7. Standard format
7
Consider the following 5 types of possible equation in a LP problem:

8. Standard format
8
We will tell you why we need this format later!
Where, S is a slack variable

9. Sample of an LP problem

9

10. Standard format

10

11. Difference b/w Original and Standard

11
Original LP format Standard LP format
Slack Variables!


12. More example of standard format
12
 Consider the following:
We can see that min has be converted to max and slack variables are added.

13. 2. Simplex Tableau
13

14. Simplex Tableau
 The simplex method progresses through a series of adjacent extreme points
(basic feasible solutions) with increasing values of the objective function
 Each such point can be represented by a simplex tableau, a table storing the
information about the basic feasible solution corresponding to the extreme
point.
 For Example:
푚푎푥푖푚푖푧푒
3푥 + 5푦 + 0푢 + 0푣
푠푢푏푗푒푐푡 푡표
푥 + 푦 + 푢 = 4
푥 + 3푦 + + 푣 = 6
푥, 푦, 푢, 푣 ≥ 0.
14

15. Simplex Tableau
푢
푣
푥 푦 푢 푣
1 1 1 0 4
1 3 0 1 6
-3 -5 0 0 0
Initialized by the
coefficients of the
objective function. The
signs are reversed in this
row (objective row)
We have constraints + 1
rows and variables +1
columns
Pivot Column/Entering Variable.
In our example, its Y
15

16. Simplex Tableau
3.Pivot Column
 Objective Row:
 The objective row is used by the simplex method to check whether the current
tableau represents an optimal solution.
 It does have the optimum solution if all the entries in the objective row—except, possibly,
the one in the last column—are nonnegative.
 Pivot Column/Entering Variable:
 Select the minimum number in the objective row, such a choice yields the largest
increase in the objective function’s value per unit of change in a variable’s value.
The most negative one selected will be the pivot column with an entering variable.
It is indicated by the up arrow.
16

17. Simplex Tableau
4. Calculating the Theta Ratio and Departing Variable
 Departing Variable:
 Also called leaving variable or pivot row i.e., a basic variable to become non basic
in the next tableau. Indicated by
 How to calculate:
 For each positive entry in the pivot column, compute the θ-ratio by dividing the
row’s last entry by the entry in the pivot column.
 The row with the smallest θ-ratio determines the departing variable, i.e., the
variable to become non basic.
 If there are no positive entries in the pivot column, no θ-ratio can be computed,
which indicates that the problem is unbounded and the algorithm stops.
17

18. Simplex Tableau
Calculating the Theta Ratio and Departing Variable
푢
푣
푥 푦 푢 푣
1 1 1 0 4
1 3 0 1 6
-3 -5 0 0 0
Pivot Column/Entering Variable
휃 − 푟푎푡푖표 =
4
1
= 4
휃 − 푟푎푡푖표 =
6
3
= 2
The row with the smallest θ-ratio determines the
departing variable. For our example, it is variable v.
The intersecting element of Pivot Column and Pivot
Row is the pivot.
In the next tableau the intersected element will
become 1 and the rest of elements will become 0 in
the pivot column.
Departing Variable / Leaving Variable/ Pivot Row
18

19. 5. Pivoting
 To transform the current tableau into the next one and increase the value of
the objective function to the next feasible solution. We have to take some
steps. Called Pivoting
 Pivoting, is similar to the principal step of the Gauss-Jordan elimination
algorithm for solving systems of linear equations.
 Steps:
1. First, divide all the entries of the pivot row by the pivot, its entry in the pivot
column, to obtain Rownew
2. Then, replace each of the other rows, including the objective row, by the
difference
 푅표푤 − 푐. 푅표푤푛푒푤
 Where c is the row’s entry in the pivot column.
19

20. Pivoting
1. Calculating Rownew
푢
푣
푥 푦 푢 푣
1 1 1 0 4
1 3 0 1 6
-3 -5 0 0 0
푅표푤푛푒푤 =
1
3
3
3
0
3
1
3
6
3
푅표푤푛푒푤 =
1
3
, 1, 0,
1
3
, 2
The pivot row will be replaced by the Rownew we calculated.
20

21. Pivoting
2. Calculating Row – c.Rownew
 As we have calculated the 2nd row. Now we will apply this formula on the rest
of the rows. i.e. Row 1 and Row 3 in our example.
 For Row 1:
 Row 1 – C. Rownew where C = 1
 1 − 1.
1
3
1 − 1.1 1 − 1.0 0 − 1.
1
3
4 − 1.2

2
3
0 1 −
1
3
2
 For Row 3:
 Row 3 – C. Rownew where C = -5
 −3 − −5 .
1
3
− 5 − (−5). 1 0 − (−5). 0 0 − (−5).
1
3
0 − (−5). 2
 −
4
3
0 0
5
3
10
Now we will replace all the rows with their new respective rows in order to make the
new tableau. 21

22. Pivoting
Next Tableau
푢
푦
푥 푦 푢 푣
2/3 0 1 -1/3 2
1/3 1 0 1/3 2
-4/3 0 0 5/3 10
Now we can see that the intersected element became 1 and the rest of them
became zero in pivot column.
The Entering variable Y took the place of departing variable V.
But…
We cannot finish here, because the objective row has still a negative value. We
have to eliminate it by doing further iterations.
22

23. 2nd Iteration
 We have to go through all the steps again. Including the selection of pivot column calculating
pivot row and then pivoting.
 So our Rownew would be: 1 0
3
2
−
1
2
3
 For Other Rows:
 For Row 2:
 Row 2 – C. Rownew where C = 1/3

1
3
−
1
3
. 1 1 −
1
3
. (0) 0 −
1
3
. (
3
2
)
1
3
−
1
3
. (−
1
2
) 2 −
1
3.
. 3
 0 1 −
1
2
1
2
1
 For Row 3:
 Row 3 – C. Rownew where C = -4/3
 −
4
3
− −
4
3
. 1 0 − −
4
3
. 0 0 − −
4
3
.
3
2
5
3
− −
4
3
. (−
1
2
) 10 − −
4
3
. 3
 0 0 2 1 14
Put in next tableau…
23

24. 2nd Iteration Tableau
푥
푦
푥 푦 푢 푣
1 0 3/2 -1/2 3
0 1 -1/2 1/2 1
0 0 2 1 14
We can see that the last row has no negative value left. We can safely stop our
iterations here.
We can conclude our maximized solution as:
푥 = 3
푦 = 1
푢 = 0
푣 = 0
푀푎푥 = 14
We choose u and v equal
to 0, because their
column has all distinct
values. If they were like
x and y, they’d have
some value.
24

25. Cycling – Bland’s Rule
 When an objective function’s values “stall” for several iterations in a row and
that the algorithm cycles back to a previously considered point and hence
never terminate. This phenomenon is called cycling.
 Although, it rarely happens, but when it does - A simple modification of the
simplex method, called Bland’s rule, eliminates even the theoretical
possibility of cycling.
25

26. Cycling – Bland’s Rule
 Assuming that the variables are denoted by a subscripted letter (e.g., x1,
x2,..., xn), this rule can be stated as follows:
1. Among the columns with a negative entry in the objective row, select the
column with the smallest subscript.
2. Resolve a tie among the smallest θ-ratios by selecting the row labeled by the
basic variable with the smallest subscript.
26

27. Software Simulation
 Simplex Method has became so efficient that its calculation packages are
even available online. One of them is as follows:
 For ease, we will copy the same problem to the online tool and check
whether it gives us the same result:
maximize p = 3x +5y
subject to x + y = 4, x+3y = 6
 Simplex Method Online Tool
27

28. Efficiency
How efficient is the simplex method?
28

29. Efficiency of Simplex Algorithm
 Since we know that the algorithm progresses through a sequence of adjacent
points of a feasible region. Right?
 So, one should probably expect bad news because the number of extreme
points is known to grow exponentially with the problem size.
 The worst-case efficiency of the simplex method has been shown to be
exponential.
 But Fortunately!
 More than half a century of practical experience with the algorithm has
shown that the number of iterations in a typical application ranges between
m and 3m, with the number of operations per iteration proportional to mn,
where m and n are the numbers of equality constraints and variables,
respectively.
29

30. Other Variants of the Algorithm
 Ellipsoid Method:
 An important mile- stone in the history of such algorithms was the proof by L. G.
Khachian showing that the ellipsoid method can solve any linear programming
problem in polynomial time.
 However, ellipsoid method was much slower than the simplex method in practice
 Karmarker’s Method
 Narendra Karmarkar published an algorithm that not only had a polynomial worst-case
efficiency but also was competitive with the simplex method. This method
generates a sequence of feasible solutions that lie within the feasible region
rather than going through a sequence of adjacent extreme points as the simplex
method does. (Interior Point Methods).
30

31. Summary of Simplex Algorithm
 Step 0
 Initialization. Present a given linear programming problem in standard form and set up an initial
tableau with non negative entries in the rightmost column.
 Step 1
 Optimality test. If all the entries in the objective row are nonnegative—stop: the tableau
represents an optimal solution whose basic variables’ values are in the rightmost column and
the remaining, non basic variables’ values are zeros.
 Step 3
 Finding the entering variable. Select the most negative entry from among the first n elements
of the objective row.
 Step 4
 Finding the departing variable. For each positive entry in the pivot column, calculate the θ-
ratio. Find the row with the smallest θ-ratio.
 Step 5
 Forming the next tableau. Divide all the entries in the pivot row by its entry in the pivot
column. Subtract from each of the other rows, including the objective row, the new pivot row
multiplied by the entry in the pivot column of the row in question. (This will make all the
entries in the pivot column 0’s except for 1in the pivot row.) Replace the label of the pivot row
by the variable’s name of the pivot column and go back to Step 1. 31

32. Acknowledgment
The material presented in this lecture is adopted from; Anany Levitin.
Introduction to Design and Analysis of Algorithms, 3rd Edition
32

33. Thank You!
33