Download to read offline
Uploaded byMd.Sumon Sarder
Simple harmonic motion And its application
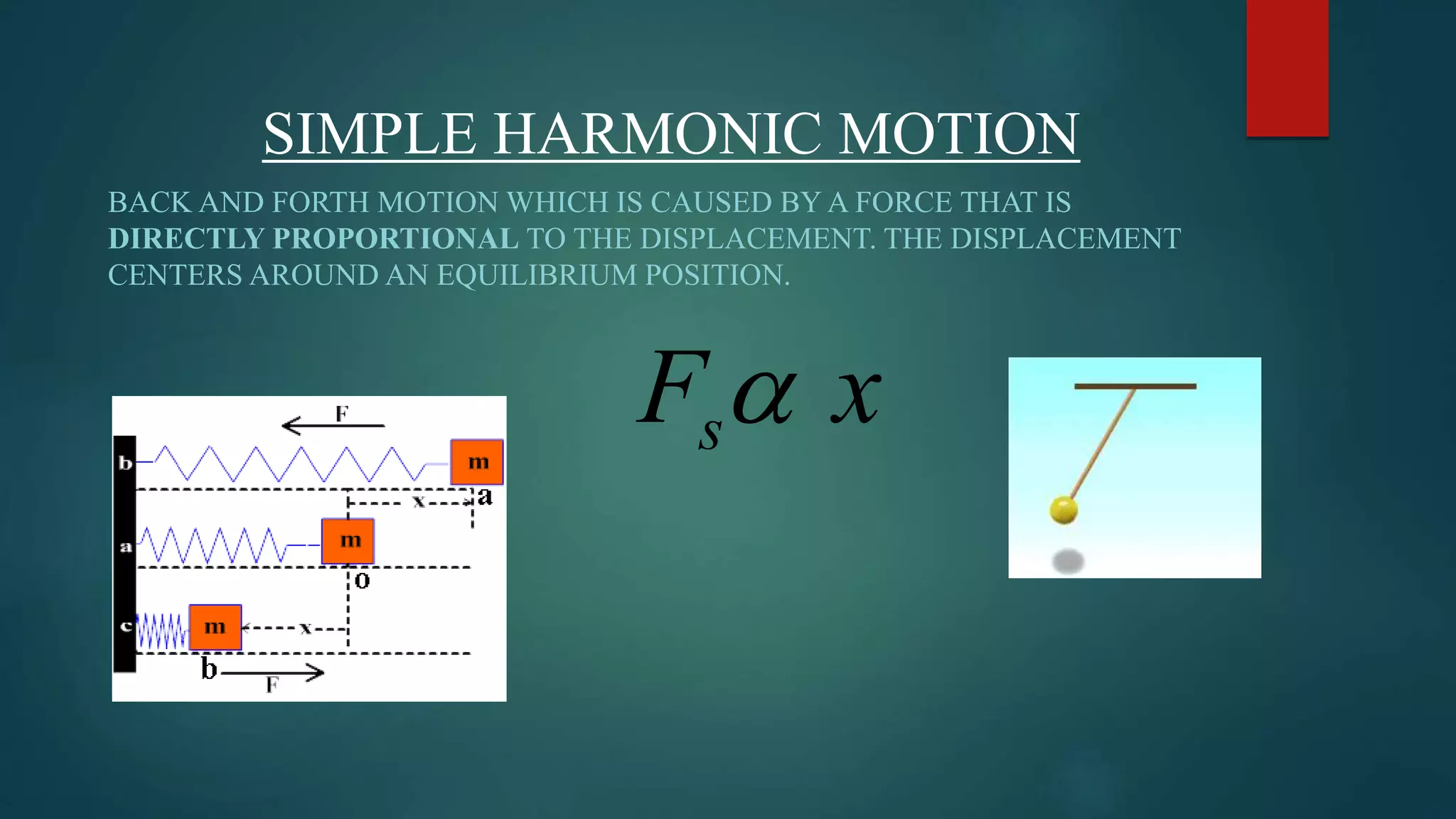
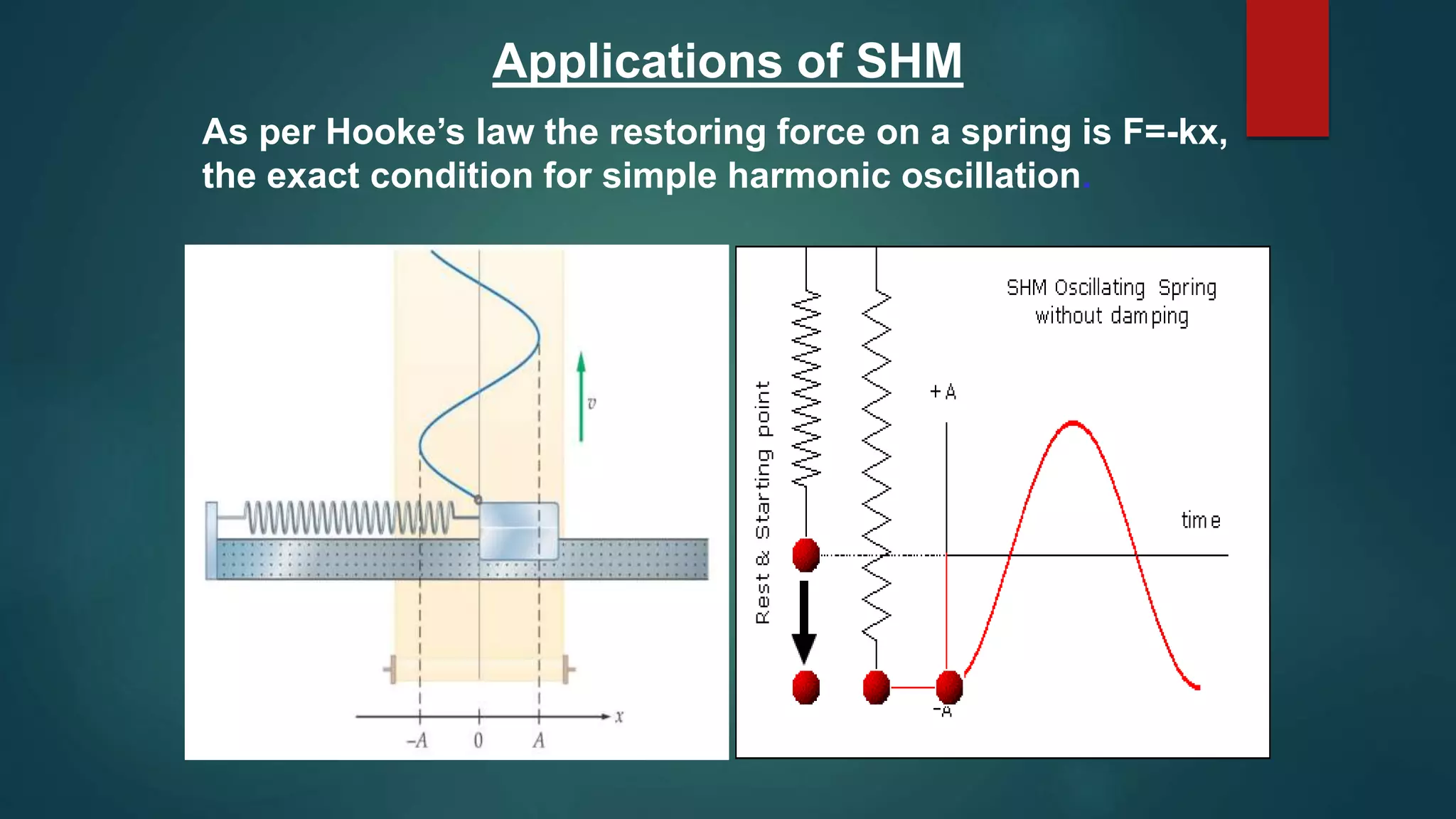
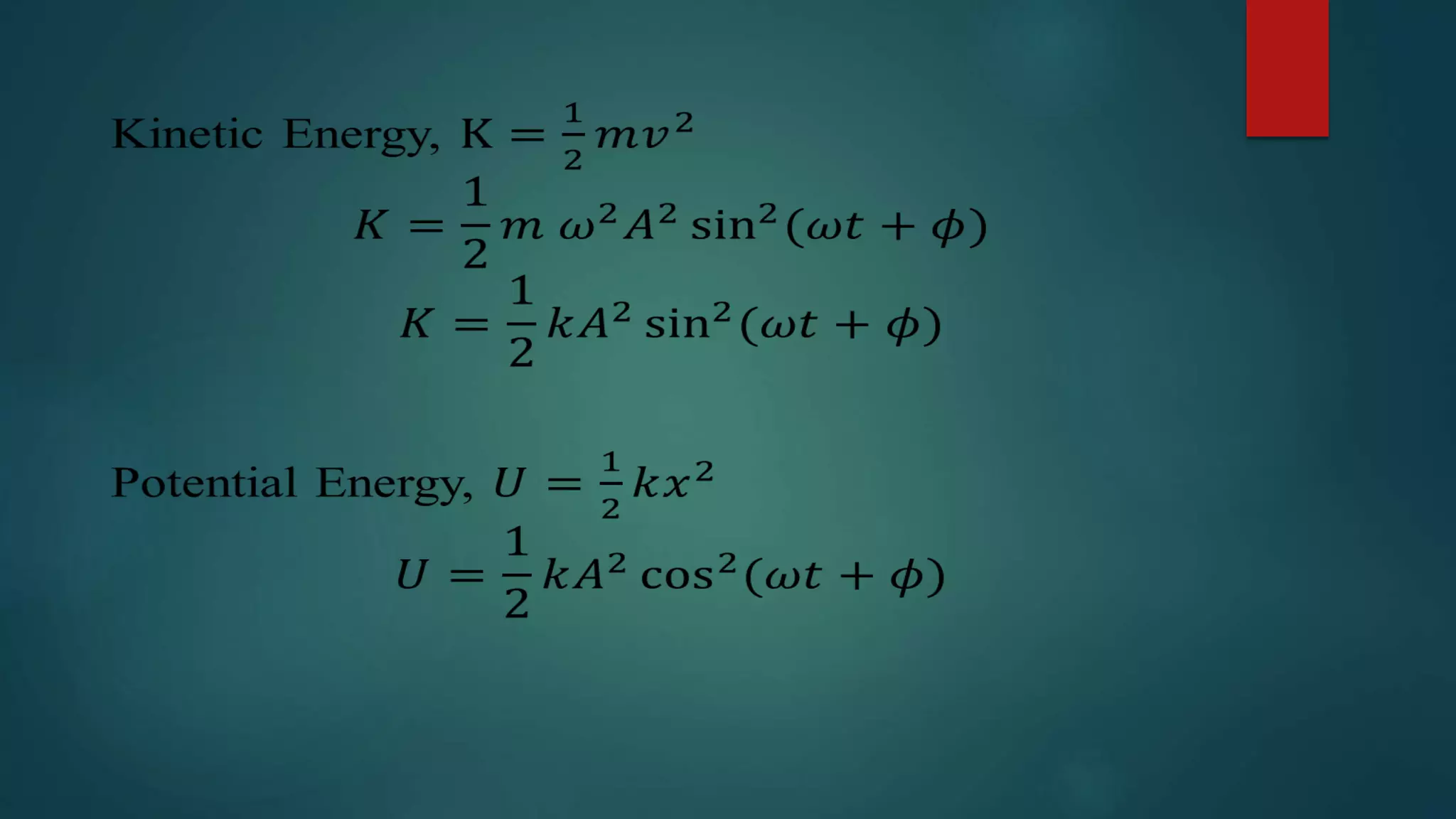This presentation introduces simple harmonic motion (SHM) and its applications. SHM describes a back-and-forth motion where the restoring force is directly proportional to displacement from the equilibrium position. One example is the motion of a spring according to Hooke's law, where the force is proportional to displacement. SHM has a differential equation and solutions that describe oscillations with a characteristic frequency and period. Common applications that exhibit SHM include springs, pendulums, and torsional oscillators.
More Related Content
Similar to Simple harmonic motion And its application
Simple harmonic motion And its application
- 1.
- 2. SIMPLE HARMONIC MOTION ANDITS APPLICATION PRESENTED BY MD. SUMON SARDER ID: 161-15-953
- 3. SIMPLE HARMONIC MOTION BACKAND FORTH MOTION WHICH IS CAUSED BY A FORCE THAT IS DIRECTLY PROPORTIONAL TO THE DISPLACEMENT. THE DISPLACEMENT CENTERS AROUND AN EQUILIBRIUM POSITION. xFs
- 4. Springs – Hooke’sLaw kxorkxF k k xF s s N/m):nitConstant(USpring alityProportionofConstant One of the simplest type of simple harmonic motion is called Hooke's Law. This is primarily in reference to SPRINGS.
- 5. Simple Harmonic Motion(SHM) Hence, In SHM the restoring force is proportional to the displacement and acts in the opposite direction of that displacement
- 6.
- 7. Value of 𝜔 Puttingthe solution in the differential equation we get the value of 𝜔 𝑑2 𝑥 𝑑𝑡2 + 𝑘 𝑚 𝑥 = 0 −𝜔2 𝐴𝑐𝑜𝑠 𝜔𝑡 + 𝜙 + 𝑘 𝑚 𝐴𝑐𝑜𝑠 𝜔𝑡 + 𝜙 = 0 𝜔 = 𝑘 𝑚
- 8. Time Period ofSHM If we increase the time t in the solution of SHM by 2𝜋/𝜔, the function becomes, 𝑥 = 𝐴𝑐𝑜𝑠 𝜔 𝑡 + 2𝜋 𝜔 + 𝜙 = 𝐴𝑐𝑜𝑠 𝜔𝑡 + 2𝜋 + 𝜙 = 𝐴𝑐𝑜𝑠 𝜔𝑡 + 𝜙 i.e. the function repeats itself after a time 2𝜋/𝜔 Therefore 2𝜋/𝜔 is the period of the motion, T. 𝑇 = 2𝜋 𝜔 𝜔 = 2𝜋 𝑇 = 2𝜋𝑓, is the angular frequency.
- 9.
- 11.
- 12. Applications of SHM Asper Hooke’s law the restoring force on a spring is F=-kx, the exact condition for simple harmonic oscillation.
- 13.
- 14.
- 15. The Physical Pendulum Ifwe locate the pivot far from the object , using a weightless cord of length L, we would have, 𝐼 = 𝑀𝐿2 𝑎𝑛𝑑 ℎ = 𝐿 Then, 𝑇 = 2𝜋 𝐼 𝑀𝑔ℎ = 2𝜋 𝑀𝐿2 𝑀𝑔𝐿 = 2𝜋 𝐿 𝑔 Which is the period of a simple pendulum!
- 16.