This document provides examples of propositional and predicate logic. It introduces basic logical concepts like propositions, truth values, connectives like "if...then" and "and", and quantifiers like "all" and "some". Propositional logic examples use letters like p and q to represent simple statements without internal structure. Predicate logic examples assign predicates like "loves" and "crazy" to arguments to represent statements with meaning, like "Loves(John, Mary)". The document explains how to represent quantified statements using predicates, arguments, and quantifiers.






























































































































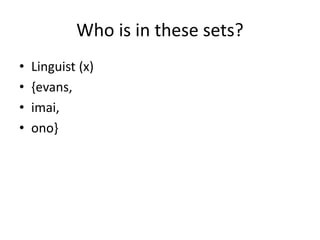


































![But Logic is VERY important in
Linguistics!
• The nurse kissed every child on his birthday.
• [The nurse] kissed [every child] on his birthday.
• Kissed (nurse, every_child)](https://image.slidesharecdn.com/sentencesemi-161019070801/85/Sentence-semantics-162-320.jpg)










