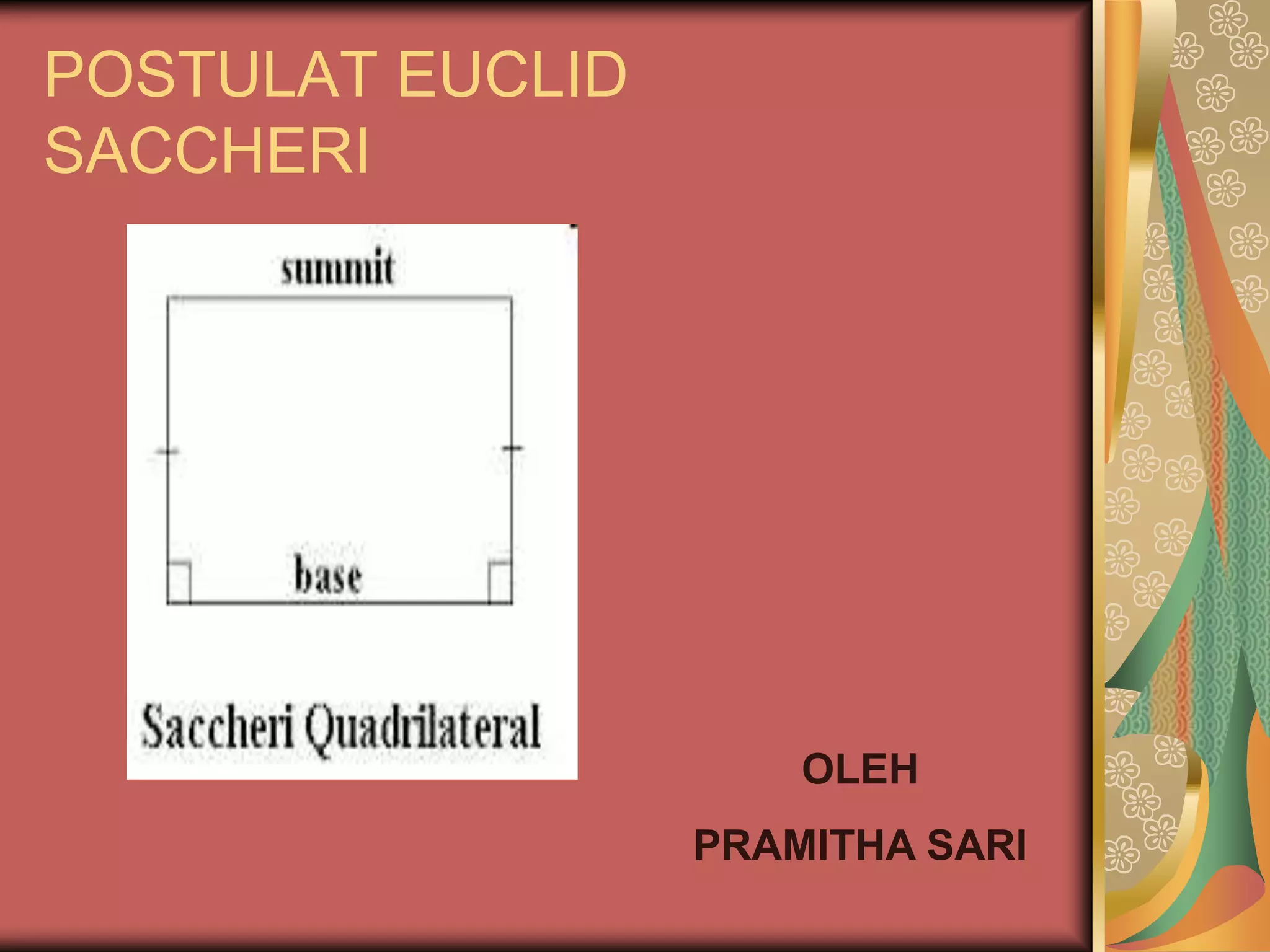
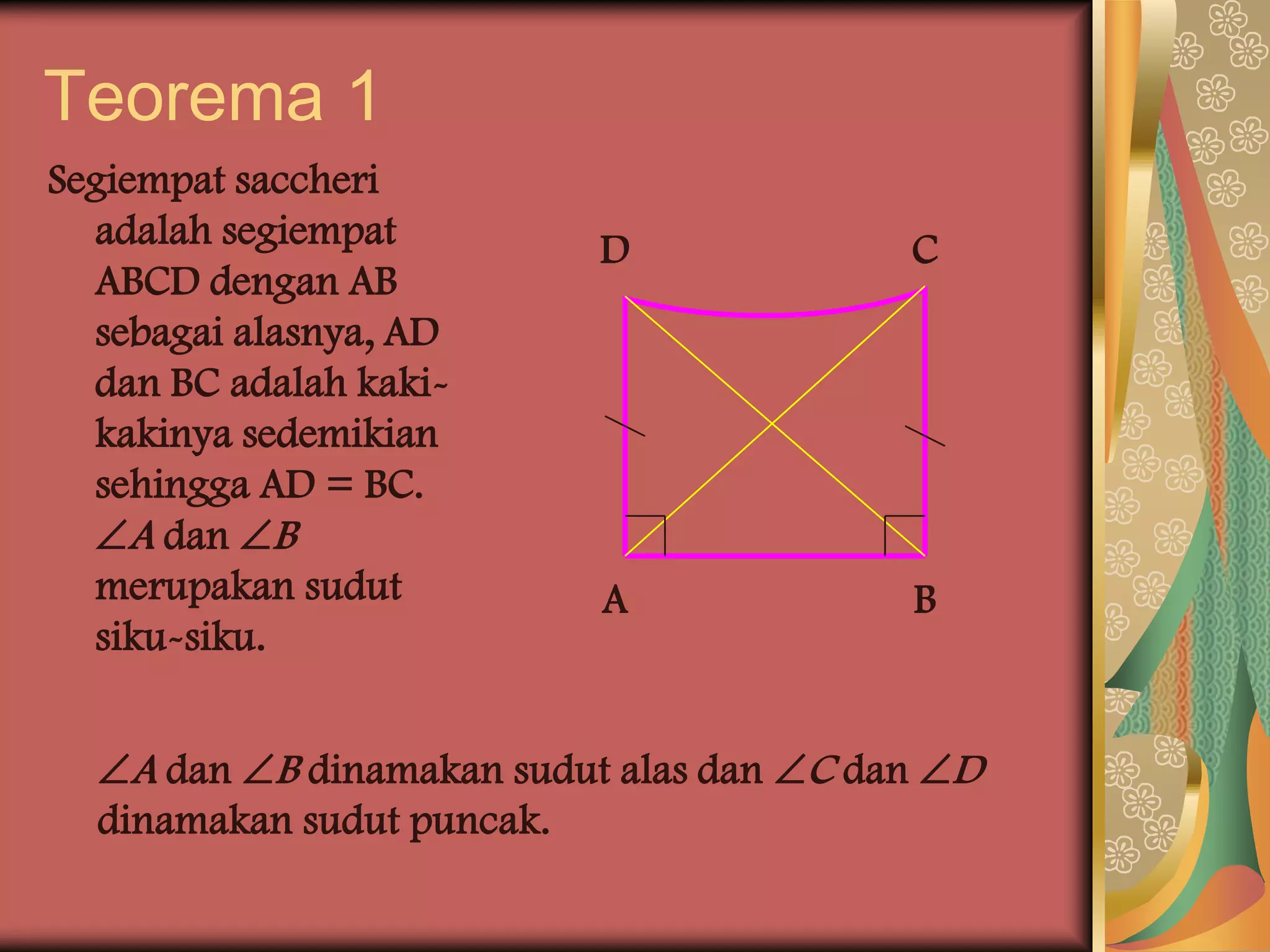
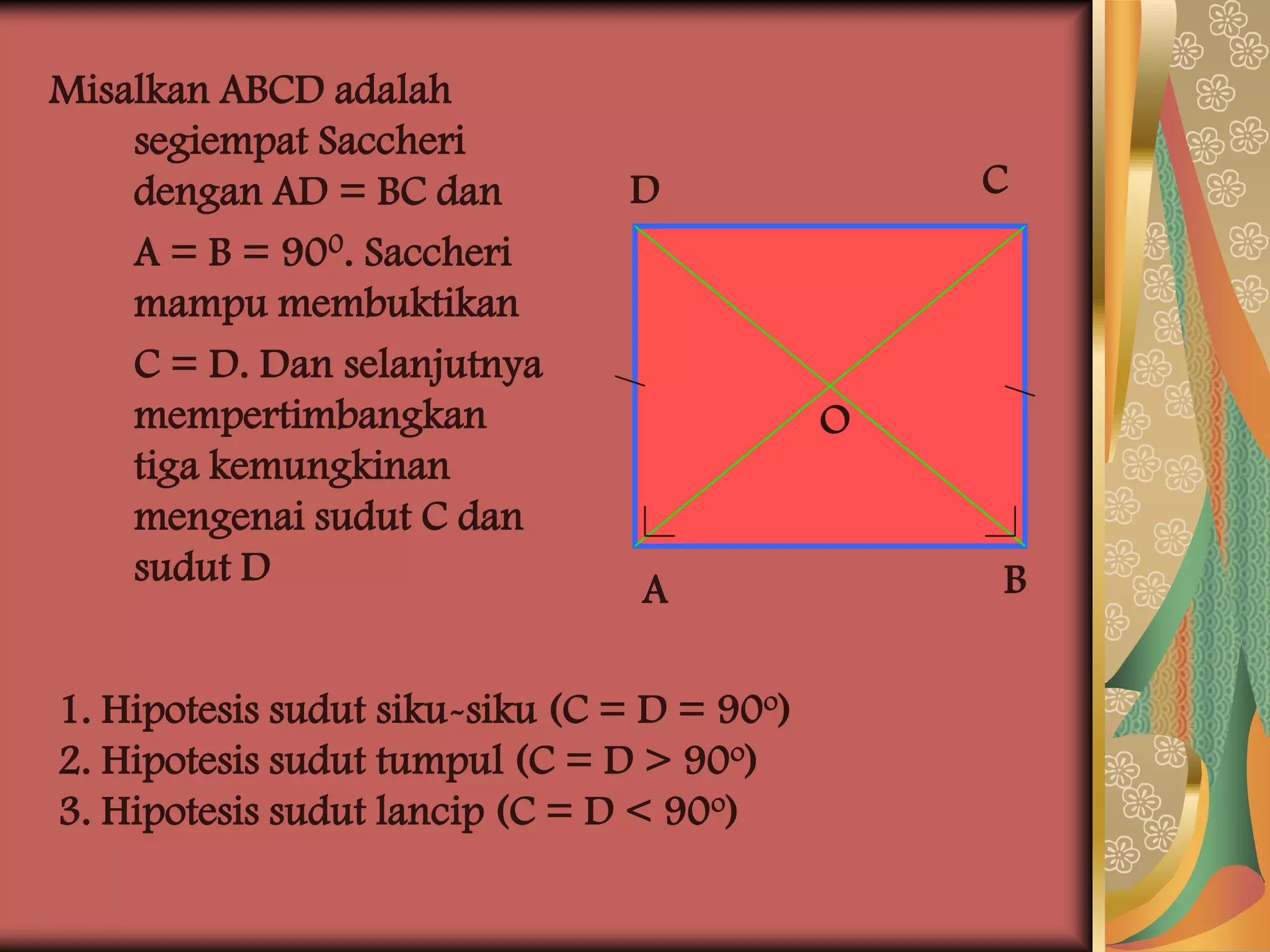
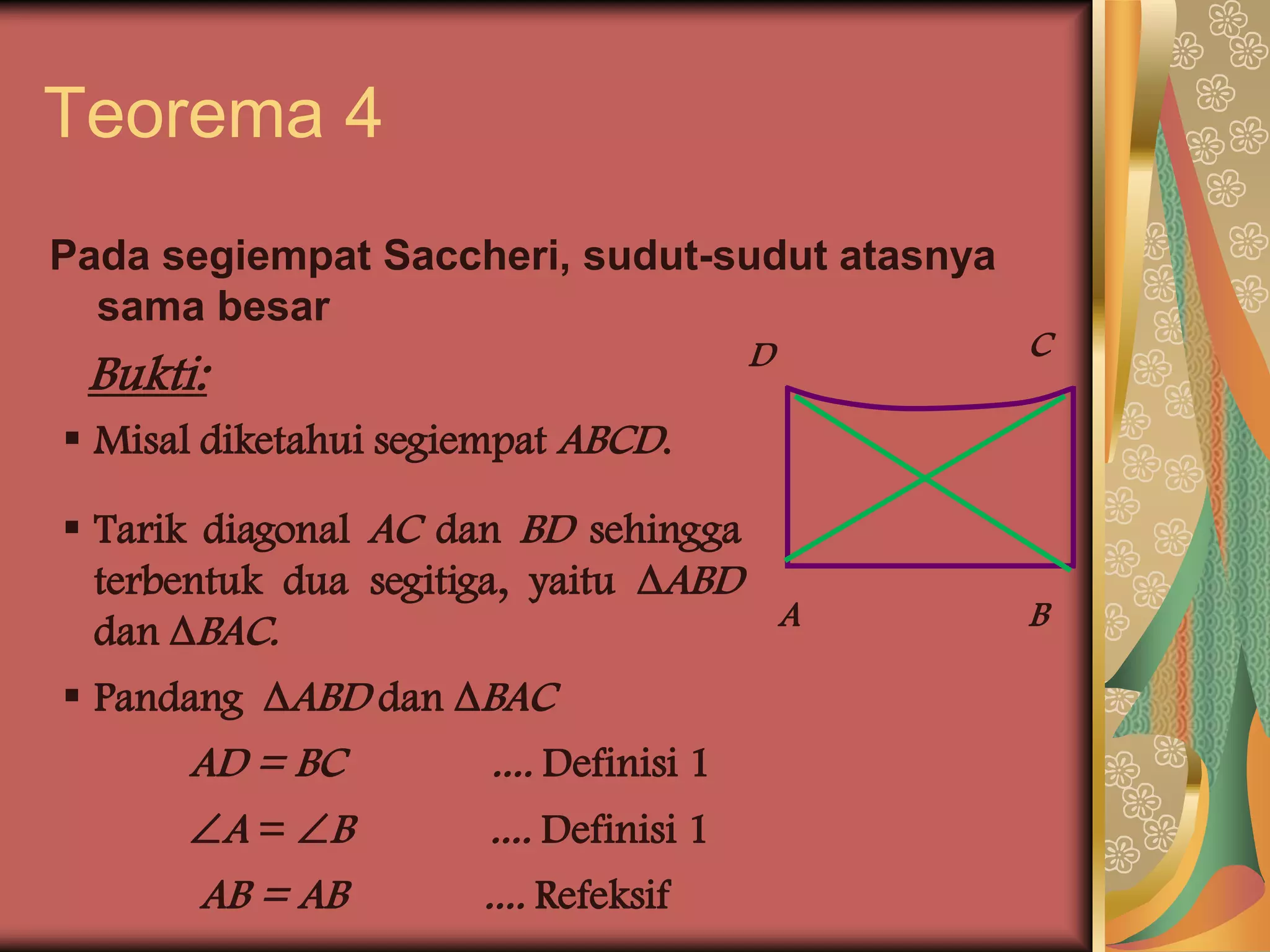
Saccheri adalah matematikawan Italia abad ke-17 yang meneliti postulat Euclid. Ia membangun segiempat khusus bernama segiempat Saccheri dan membuktikan 5 teorema tentang segiempat tersebut. Teorema terakhir membuktikan bahwa sudut-sudut atas segiempat Saccheri adalah lancip, bukan siku-siku atau tumpul. Karya Saccheri menantang postulat Euclid tentang paralel dan membuka jalan bag

1. POSTULAT EUCLID
SACCHERI
OLEH
PRAMITHA SARI

2. Giovanni Girolamo Saccheri
(5 September 1667 – 25 Oktober 1733)
Saccheri lahir di San Remo, Genoa (sekarang Italia).
Saccheri adalah anak dari seorang pengacara. Dia
mulai ikut pelatihan akademik dengan Yesuit di Genoa
pada tahun 1685 dan 5 tahun kemudian terdaftar di
Kampus Jesuit Brera untuk belajar filsafat dan
teknologi.
Saccheri meninggal di Milan, Italia pada tanggal 25
Oktober 1733. Dalam karyanya sintesis, Saccheri
memberikan analisa lengkap tentang masalah
kesejajaran dalam hal segiempat.

3. Segiempat Saccheri
Saccheri menarik garis
yang tegak lurus pada
D C
ujung-ujung dua buah
segmen garis yang
saling sejajar. Bangun
yang terbentuk ini
disebut sebagai
segiempat saccheri B
A
(Saccheri Quadrilateral)

4. Teorema 1
Segiempat saccheri
adalah segiempat D C
ABCD dengan AB
sebagai alasnya, AD
dan BC adalah kaki-
kakinya sedemikian
sehingga AD = BC.
A dan B
merupakan sudut A B
siku-siku.
A dan B dinamakan sudut alas dan C dan D
dinamakan sudut puncak.

5. Misalkan ABCD adalah
segiempat Saccheri
dengan AD = BC dan D C
A = B = 900. Saccheri
mampu membuktikan
C = D. Dan selanjutnya
mempertimbangkan O
tiga kemungkinan
mengenai sudut C dan
sudut D B
A
1. Hipotesis sudut siku-siku (C = D = 90o)
2. Hipotesis sudut tumpul (C = D > 90o)
3. Hipotesis sudut lancip (C = D < 90o)

6. Teorema 2
Sudut puncak Saccheri adalah sama (Dengan menggunakan
kelima postulat).
Bukti:
Perhatikan DAB dan CBA
DAB = CBA = 90, AD = BC, AB adalah garis lurus.
Dengan SAS postulat, DAB dan CBA adalah kongruen.
Perhatikan juga ACD dan BDC
Dimana AD = BC, AC = BD, CD adalah garis lurus.
Dengan SSS postulat, ACD dan BDC adalah kongruen.
Juga ACD = BDC, sehingga OD = OC dan OB = OA.

7. Teorema 3
Garis yang menghubungkan titik-titik tengah dari dasar
dan puncak tegak lurus terhadap keduanya.
Bukti:
M adalah titik tengah AB dan N adalah titik tengah DC.
Dengan teorema sebelumnya OD = OC,
DN = CN, dan ON = OM.
D N C
O
A M B

8. Dengan SSS postulat, OCN dan ODN adalah
kongruen. Sehingga CNO = DNO = 90, yaitu ON
tegak lurus terhadap CD.
Demikian pula, OAM dan OBM adalah kongruen.
Sehingga OAM = OBM = 90, yaitu OM tegak
lurus terhadap AB.
Selain itu, CNO = DON, COB = DOA, BOM =
AOM.
Jadi, CON + COB + BOM = DON + DOA +
AOM = 180.
MON adalah garis lurus, dimana MN tegak lurus
terhadap AB dan CD.

9. Teorema 4
Pada segiempat Saccheri, sudut-sudut atasnya
sama besar
D C
Bukti:
 Misal diketahui segiempat ABCD.
 Tarik diagonal AC dan BD sehingga
terbentuk dua segitiga, yaitu ABD
dan BAC. A B
 Pandang ABD dan BAC
AD = BC .... Definisi 1
A = B .... Definisi 1
AB = AB .... Refeksif

10. Berdasarkan sisi-sudut-sisi maka ABD  BAC
akibatnya AC = BD
 Pandang ACD dan BDC
AD = BC .... Definisi 1
AC = BD .... Akibat ABD  BAC
DC = DC .... Refeksif
Berdasarkan sisi-sudut-sisi maka ACD  BDC
akibatnya D = C.
Jadi, terbukti bahwa sudut-sudut atas segiempat
Saccheri sama besar.

11. Teorema 5
Pada segiempat Saccheri, sudut-sudut atasnya lancip.
Bukti:
 Berdasarkan Akibat 1 Teorema 3, yaitu jumlah besar
sudut-sudut dalam segiempat kurang dari 360 maka
A + B + C + D < 360
90 + 90 + C + D < 360 .... Definisi 1
C + D < 180
2C < 180 .... Teorema 4
C < 90
Jadi, terbukti bahwa C dan D adalah lancip.

12. Latihan soal:Latihan soal.doc

13. Daftar Pustaka
http://academic.brcc.edu/ryanl/modules/geometry/qu
adrilaterals/quad_sacc.html
http://en.wikipedia.org/wiki/Giovanni_Girolamo_Sacc
heri
http://web.mnstate.edu/peil/geometry/c2euclidnoneu
clid/6Saccheri.htm
http://www.google.co.id/url?sa=t&rct=j&q=&esrc=s&s
ource=web&cd=5&cad=rja&ved=0CDQQFjAE&url
=http%3A%2F%2Fwww.ms.uky.edu%2F~droyster
%2Fcourses%2Fspring02%2Fclassnotes%2FCha
pter04.pdf&ei=6oZRUNvTNY7KrAeGkYCgDQ&us
g=AFQjCNHv4jKycmaqgCXl87OGVHX5fidU2A&si
g2=spD0KHTTzTTd2-nbIktRyA

14. SEKIAN
DAN
TERIMA KASIH