2015年度英語教育リサーチメソッド第4・5回

1. 英語教育
リサーチメソッド
第４・５回
May 13th, 2015
亘理 陽一
eywatar@ipc.shizuoka.ac.jp

2. 第4・5回: 記述統計(1)・(2)
• 前回の感想から
• タスク：データの把握と可視化／要約統計量
による整理
• 講義：データの可視化と尺度水準／記述的指
標とその性質
• 課題3

3. Questions & Feedback
• 総合的・分析的か探索的・演繹的は自分のやりたい方、感覚で選んでいい
のか。
• 質的研究を長く行うことで、量的研究のような「一般化」を導くことは可
能ではないだろうか。
• 妥当性を考える時に、これが妥当だ！とかこれなら妥当だ！と判断する際
も、自分の価値判断が働いてしまっているような気がします。かといっ
て、客観的側面から妥当性を実証するためには、いろんな方にこれが妥当
か確かめたりして妥当性を高めていくのでしょうか？
• 量的研究において、横断的に研究を行う際に、集団毎にあらゆる観点にお
ける格差が生まれることが予想されるが、その場合はどのように対処した
らよいのだろうか。

4. Task 1

5. Task 1
第2回Task 2集計シート
http://bit.ly/RM20150513SQ

6. Task 1
• Q1. 回答者の人数(n)は（ ）人で，内女性が
（ ）人，男性が（ ）人。
• Q2. 回答者の通学時間は平均（ ）分である。
• Q3. 恋愛力尺度1の平均値は（ ），恋愛力尺
度2の平均値は（ ），恋愛力尺度3の平均値
は（ ），恋愛力尺度3問の合計得点の平均点
は（ ）である。
25
13 12
29.52
3.56
3.20
4.24
11.00

7. Task 1
• Q2. 回答者の通学時間
• 図4.1. ヒストグラム
• 度数: 人
• 階級値: 0∼150分（15分ごと）

8. Task 1
• Q3. 恋愛力尺度合計得点
• 表4.1. 度数分布表
• 度数（人数n）: 女性 13/ 男性 12
• 平均: 女性＿＿＿/ 男性＿＿＿
• 恋愛感情に男女差はあるか？
11.23 10.75

9. Task 1
• Q4. 聞く話す読む書くの4技能の内，重要度が高かっ
たのは順に，
• 1: 2: 3: 4:
• Q5. 中学校で使用していた教科書は多い順に，
• 1: 2: 3: 4: 5:
聞く 書く
NH TE SS NC C21

10. ４つの尺度水準
• 比(率)尺度: それぞれの目盛りの間隔も等しく、0の点が
ある…通学時間
• 間隔尺度: それぞれの目盛りの間隔は等しいが、絶対的
な0の点はない…恋愛尺度得点
• 順序尺度: それぞれの目盛りの間隔が等しいとは限らな
い…4技能重要度
• 名義尺度: 単に属性を割り振っただけ…教科書

11. ４つの尺度水準
• 西暦年: 例. 1980年
• 血液型: 例. AB型
• 身長、体重: 例. 173.5cm、64kg
• 成績の順位: 例. 3位

12. ４つの尺度水準
• 比(率)尺度: それぞれの目盛りの間隔も等しく、0の点が
ある…通学時間、身長・体重
• 間隔尺度: それぞれの目盛りの間隔は等しいが、絶対的
な0（無）の点はない…恋愛尺度得点、西暦年
• 順序尺度: それぞれの目盛りの間隔が等しいとは限らな
い…4技能重要度、成績の順位
• 名義尺度: 単に属性を割り振っただけ…教科書、血液型

13. 尺度と情報量（テキストp.34）
名 義 尺 度 く 順 序 尺 度 く 間 隔 尺 度 く 比 例 尺 度
情報量小……………………………………･ …………･ …・情報量大
▲図３−１尺度と情報量
B ､ 巳『みなす」という行為
前節で，テストの得点は間隔尺度であると書きました。しかし，これ
は厳密にいうと，正しくないのかもしれません。たとえば，英語テスト

14. 尺度と情報量
• 変数変換（測られた変数の値を他の値に変えるこ
と）の可能性
• 比率尺度: 定数倍（変数にある数をかける）
• 間隔尺度: ＋線形変換（全てに同じ数を±）
• 順序尺度: ＋単調変換（順序関係保つ変換）
• 名義尺度: ＋一対一変換（他の何かに置換）

15. 尺度と情報量
• 変数変換（測られた変数の値を他の値に変えるこ
と）の可能性
• 比率尺度: ○150→1.5, ×50+10, 75+10
• 間隔尺度: ○それぞれの恋愛得点に+50
• 順序尺度: 学級 1, 2, 3 → 学年 1, 2, 3, 4, 5, 6,
• 名義尺度: ○1→4、3→1、…

16. Task 2

17. Task 2
• ４つの尺度水準のどれに当てはまるかを分類
• 英語学習の好き嫌い / 英語学習年数 / 英語話者の知
人・友人の数 / 学習方法についてのアンケート / 海
外旅行・留学経験の有無 / 学籍番号 / 家庭での学習
時間 / 欠席回数 / 期末テスト（100点満点）/ 使用教
科書 / 通学時間 / 単位評定 / 単語テスト（10点満点）
/ TOEICスコア / 平常点 / WPM

18. Task 2
• 名義尺度: 海外旅行・留学経験の有無、学籍番号、単位評定、使
用教科書
• 英語学習の好き嫌い、学習方法アンケート
• 順序尺度∼間隔尺度: 平常点、期末テスト（100点満点）、単語テ
スト（10点満点）、TOEICスコア
• 間隔尺度であると仮にみなして処理している
• 比率尺度: 英語学習年数、英語話者の知人・友人の数、家庭での
学習時間、欠席回数、通学時間、WPM

19. 記述的指標とその性質
• 記述統計（vs. 推測統計）
• 得られたデータをまとめて、「このデー
タの特徴は〇〇ですよ」と記述する統計
• 目的は、たくさんのデータを整理してわ
かりやすく表現すること

20. 記述的指標とその性質
• 代表値: データ全体をたった１つで代表させる値
• 平均（Mean, M）: データの全ての値をたし加
えて、データの個数で割ったもの
• 中央値: データを小さい（大きい）順に並べ替
えたときに、ちょうど真ん中にくる値
• 最頻値: 最も度数の多いデータの値

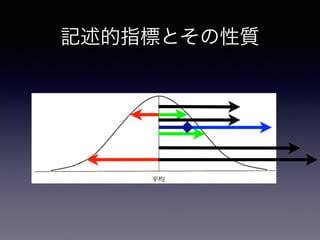
21. 記述的指標とその性質（テキストp. 124）
Ｙ
◆
傘 ◆ ◆
･･電念三．◆
､
外れ{ I 娠貞しり) 嶋介
ノ･琴.4９
◆●●●●｡●●｡●●●●●通り4
； ：◆
も
心
●●●●Q●●p●凸｡●●■
外れ赦込簿' > 蝿介
ﾉ ･ 圭. 甑
▲図９−２外れ値が相関係数に影響を与えている例

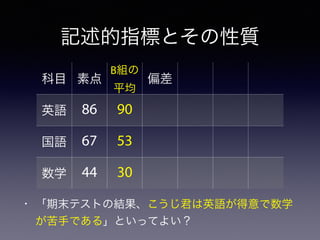
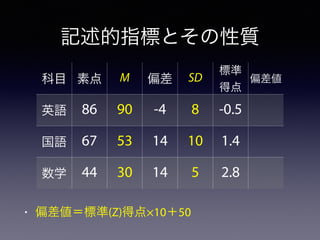
22. 記述的指標とその性質
• 代表値: データ全体をたった１つで代表さ
せる値
• 例. 単語テストの結果
• A組: 4, 4, 5, 5, 5, 5, 6, 6
• B組: 1, 2, 3, 5, 5, 7, 8, 9

23. 記述的指標とその性質
• 散布度: どれだけ散らばっているか（ばらつき）
• 値が小さい＝平均付近に値が集中
• 偏差: 個々の値の平均・中央値からのズレ→平均偏差
• 分散: 偏差を２乗してその平均をとったもの
• 標準偏差（SD）: 分散の√
• 範囲: データの最大値と最小値の差

24. 記述的指標とその性質

25. Task 2

26. Task 2
• Q2. 恋愛感情得点合計(/15)
• 表3.1. 度数分布表
• 標準偏差: 女性＿＿＿/ 男性＿＿＿
• 範囲: 女性＿＿＿/ 男性＿＿＿
• 恋愛感情に男女差はあるか？

27. 記述的指標とその性質
• 「期末テストの結果、こうじ君は英語が得意で数学
が苦手である」といってよい？
科目 素点
英語 86
国語 67
数学 44

28. 記述的指標とその性質
• 「期末テストの結果、こうじ君は英語が得意で数学
が苦手である」といってよい？
科目 素点
B組の
平均
偏差
英語 86 90
国語 67 53
数学 44 30

29. 記述的指標とその性質
• 「期末テストの結果、こうじ君は英語が得意で数学
が苦手である」といってよい？
科目 素点
B組の
平均
偏差
標準
偏差
英語 86 90 -4 8
国語 67 53 14 10
数学 44 30 14 5

30. 記述的指標とその性質
• 標準化: データの値から平均をひいて標準偏差でわ
ること
科目 素点
B組の
平均
偏差
標準
偏差
英語 86 90 -4 8
国語 67 53 14 10
数学 44 30 14 5

31. 記述的指標とその性質
• 標準化: データの値から平均をひいて標準偏差でわ
ること
科目 素点
B組の
平均
偏差
標準
偏差
英語 86 90 -4 8
国語 67 53 14 10
数学 44 30 14 5

32. 記述的指標とその性質
• 標準化: データの値から平均をひいて標準偏差でわ
ること
科目 素点
B組の
平均
偏差
標準
偏差
標準
得点
英語 86 90 -4 8
国語 67 53 14 10
数学 44 30 14 5

33. 記述的指標とその性質
• 標準得点=Z得点: 数学(2.8)＞国語(1.4)＞英語(-0.5)
科目 素点 M 偏差 SD
標準
得点
英語 86 90 -4 8 -0.5
国語 67 53 14 10 1.4
数学 44 30 14 5 2.8

34. 記述的指標とその性質
• 偏差値＝標準(Z)得点×10＋50
科目 素点 M 偏差 SD
標準
得点
偏差値
英語 86 90 -4 8 -0.5
国語 67 53 14 10 1.4
数学 44 30 14 5 2.8

35. 記述的指標とその性質
• 偏差値＝標準(Z)得点×10＋50
科目 素点 M 偏差 SD
標準
得点
偏差値
英語 86 90 -4 8 -0.5 45
国語 67 53 14 10 1.4 64
数学 44 30 14 5 2.8 78

36. 記述的指標とその性質
• Q6: あなたの「通学時間偏差値」は（ ）
• Q7: あなたの「恋愛力偏差値」は（ ）

37. 記述的指標とその性質（テキストp. 124）
Ｙ
◆
傘 ◆ ◆
･･電念三．◆
､
外れ{ I 娠貞しり) 嶋介
ノ･琴.4９
◆●●●●｡●●｡●●●●●通り4
； ：◆
も
心
●●●●Q●●p●凸｡●●■
外れ赦込簿' > 蝿介
ﾉ ･ 圭. 甑
▲図９−２外れ値が相関係数に影響を与えている例

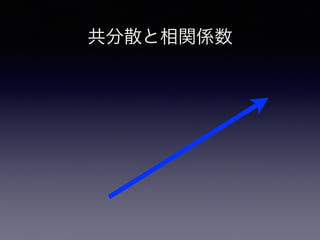
38. 共分散と相関係数
• 共分散: xとyの「平均からの偏差」の積の平均
• プラスなら右肩上がりの傾向; マイナスなら右肩下がりの傾向
たくさんあれば，散布図が右上がりになり，その場合，偏差の積の平均である
共分散の値はプラスになります。
一方，●は”i とｙ＃の片方が平均を上回り，もう片方が平均を下回る被験者
です。この●がたくさんあるということは，散布図が右下がりになるというこ
とです。●は雄とｙｉの片方が平均を上回り（偏差はプラスになる) ，もう片方
が平均を下回る（偏差はマイナスになる）わけですから，偏差の積はプラス×
マイナスで「マイナス」になります。●の点がたくさんあれば，散布図が右下
ｙ
ｙ
■
■
■
感
鰯
鰯 鰯
■ ■
■
■ ■ ■
鰯
職
■
×
■
■
■
Ｘ

39. 共分散と相関係数

40. 共分散と相関係数
• ピアソンの積率相関係数: 共分散をそれぞれの標準偏差の積で
割った値
• 2変数間にどの程度，直線的な関係があるか
• 結果の数値は−1 ≦ r ≦ 1の範囲
• 正の相関（0＜r≦1）、無相関（r = 0）、負の相関（−1≦r＜0）
• 結果の解釈の基準は絶対的なものではなく研究対象によって判断

41. 共分散と相関係数

42. 共分散と相関係数

43. 共分散と相関係数

44. 共分散と相関係数
• Q8: 恋愛力尺度間の相関は表4.3のようにまとめられる。
1 r 0 : x
Q8: 4.3
Table 4.3.
恋愛力尺度の相関行列
(1) (2) (3)
(1) 1
(2) ＿＿＿＿ 1
(3) ＿＿＿＿ ＿＿＿＿ 1
たとえば，相関係数の値がγ＝0 . 6 5 であったら「中程度の正の相関がある」
と評価し，γ＝- 0 . 8 1 であったら「強い負の相関がある」と解釈するわけです。
ですが，以上の表3 . 3 . 6 はあくまでも目安です。変数の内容，研究分野などに
よって大きく変わってくるでしょう。たとえば医学などで，人の生死にかかわ
る研究ですと，0 . 2 程度の値でも承のがせない結果になるかもしれません。
r＝０．６ r＝０．８
→ほとんど相関なし
→弱い相関あり
→中程度の相関あり
→強い相関あり
２
４
７
０
０
０
０
一
一
一
く
く
く
く
γ
γ
γ
γ
く
一
一
く
一
一
く
一
一
く
一
一
２
４
７
０
０
０
０
︲
一
一
一
一
② ９ 本 に よ っ て 表 現 が 異
なる場合があります。吉田
(1998）（Ｅ官旨ﾆｱﾆｰ可
参照）では，0 . 4 ＜￨ γ￨ ≦0 . 7
を「比較的強い相関あり」
としています（0 . 4 ＜￨ γ￨ ≦
0 . 7 とは，0 . 4 ＜γ≦0 . 7 ,
- 0 . 7 ≦γ＜−０．４というこ
とです) 。
２
４
７
０
０
０
０
︲
く
一
一
く
一
一
く
一
一
く
一
一
γ
γ
γ
γ
く
く
く
く
０
２
４
７
０
０
０
r＝１．０
表3 . 3 . 6 相関係数の値の評価
図3 . 3 . 1 相関係数と散布図
Ｑ相関係数の値と関係の強さ
それでは，相関係数がどの程［
いのでしょうか。
ﾗブ
それでは，相関係数がどの程度の値であれば，関係が強いと判断するのがよ
いのでしょうか。
この「相関係数の値の評価」については明確な基準はありませんが，通常次
ｑ９
の表３．３. 6 のように解釈されることが多し､ です。
たとえば，相関係
と評価し，γ＝- 0
ですが，以上の表3
よって大きく変わっ
る研究ですと，0 .
０
０
０
“
図３．１
図3 . 1 . 4 は，「逆Ｕ字型曲
数j r が大きくなると「前半」
も，「後半」からｙは小さくな
たとえば，２４人の被験者を
中度」を測定したとします。
への集中度」をとって，各人
●現実の散布図の例
それでは，最後に実際の散（本）
布図の例を１つ紹介しておき４０
ましよう。図3 . 1 . 6 はプロ野３５
球選手（日本人野手）の中で，3 0
2 0 0 4 年度の年俸が5 0 0 0 万円以２５
上の選手を対象として散布図２０
を描いたものです。この散布１５
図では，横軸に推定年俸をと１０
り，縦軸には2 0 0 3 年シーズン５
のホームラン数をとってあり０
ク
◆
Ｘ
◆
◆
図３．１．５無相関の散布図
ら ３ こ こ で 紹 介 し た 散 布
図は代表的な例であって，
実際のデータから描かれる
散布図すべてが上記の５つ
のパターンのいずれかに分
類されるというわけではあ
りません。しかし，心理学
の領域では，ここで紹介し
た５つの散布図の例を理解
しておけばよいでしょう。
最後に図3 . 1 . 5 は「無相関」といいます。点の集まりは全体的に「まんま
る」です。まんまるということは，２変数がでたらめに散らばっているという
ことですから，何も規則性らしぎものがないわけです。
以上のように，散布図を描くことで，２変数間の関係を視覚的に捉えること
ｑ３
ができます。散布図は，２変数の分析の出発点とし､ えます。
数の間には，右上がりの直線関係，すなわち，正の相関関係があることがわか
りますよね。つまり，年俸が高い人ほど，よくホームランを打つ傾向があると
いうことです。みなさんもこのように，自分の身近なデータについて，散布図
を描いてふてください。そうすることによって，２つの変数の関係を知るため
に散布図を描くことのおもしろさを実感できるでしょう。
◆
◆
ます。０１００００2 0 0 0 0 3 0 0 0 0 4 0 0 0 0 5 0 0 0 0 6 0 0 0 0 ( 万円）
図3 . 1 . 6 プロ野球選手の年俸（横軸）とホームラン数（縦軸）の散布図この散布図をみると，２変
図3 . 1 . 3 Ｕ字型曲線相関の散布図
Ｘ
図3 . 1 . 3 は，「Ｕ字型曲線相関」といいます。単純に「右上がり」とか「右
下がり」ではなく，両者をミックスした感じ，すなわち，一方の変数妬が大き
くなると「前半」のうちは他方の変数ｙは小さくなっていくけれども，「後半」
からｙは大きくなっていく，という関係です。
たとえば，「養毛剤の使用量」と「抜け毛の量」を考えてゑましよう。抜け
毛に悩む2 4 人各々について，「養毛剤の使用量」と「抜け毛の量」を測定し，
横軸に「養毛剤の使用量｣ ，縦軸に「抜け毛の量」をとって，各人をプロット
していったら上記の図になったとしましょう。養毛剤の量があまりに少ないと，
成分が効きませんから抜け毛は多いまま，適度に使うと抜け毛が減るけれども，
使いすぎると今度はどんどん毛穴がつまって抜け毛が多くなっていく，と思わ
れます。
ｙ
◆
◆ ◆
◆
◆
◆
◆
◆
◆
◆
◆
◆ ◆
◆
◆
◆
図３．１．４逆Ｕ字型曲線相関の散布図
◆
◆
◆
◆
◆
◆
◆
◆
Ｘ
図3 . 1 . 4 は，「逆Ｕ字型曲線相関」といいます。図3 . 1 . 3 の逆です。一方の変
数j r が大きくなると「前半」のうちは他方の変数ｙは大きくなっていくけれど
も，「後半」からｙは小さくなっていきます。
たとえば，２４人の被験者を対象に「自分の勉強部屋の音量」と「勉強への集
中度」を測定したとします。横軸に「自分の勉強部屋の音量｣ ，縦軸に「勉強
への集中度」をとって，各人をプロットしていったら上記の図になったとしま
0.24
0.50 0.04

45. 構成概念＞下位尺度＞質問項目

46. 課題3
• ワタヨー中学校3年B組で前期に行った2回のスピーキ
ングテスト(20点満点)の結果（RM20150513Kadai3）
• 図表や代表値を用いて、この結果および3年B組の生徒
のスピーキング力について所見を述べよ（最大でA4一
枚程度）
• 当該テストは妥当かつ信頼性も高いものとする
• 5月20日16時5分まで、LiveCampusを通じて提出

47. Task 3

48. Task 3
• 順に各自の研究計画を
報告・共有
• 報告に対し質問orコメ
ントがあれば遠慮なく
• グループの研究テーマ
の方向性を話し合う

49. 連絡
• テキスト第3章を読んでおく（復習）
• 課題3提出
• 次回5月20日: 推測統計の考え方
• 教室: B217、16:05開始
• 課題4を出します