1. 英語教育
リサーチメソッド
第４回
May 7th, 2014
!
!
!
亘理 陽一
eywatar@ipc.shizuoka.ac.jp

2. 基本統計量の出し方・扱い方
• 偏差＝データの値−平均
• 標準偏差＝ STDEVP() or 分散の√、√→SQRT()
• 四捨五入して小数点第２位で える
• 「データ分析」→「基本統計量」→「統計情報」
チェック（ただし不偏分散として算出される）

3. 基本統計量の出し方・扱い方
10111213141516
Factor 1 (Error bars show 95% CI)
Level
1 2 3
●
●
●

4. 基本統計量の出し方・扱い方
●
● ●
●
● ● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●●
●
●
● ●
●
5 10 15 20
5
10
15
20
Data 1
Data2

5. 第4回: 推測統計・統計的仮説検定の考え方
• 前回の感想から
• タスク：標本と母集団／母集団分布の仮定・推
測／母分散σ2が既知の場合の１つの平均値の検定
• 講義：データの質（妥当性と信頼性）／推測統計
の考え方／統計的仮説検定の手順
• 課題

6. Feedback
• 作業と理解で手一杯になってしまい，内容を教育と
結びつけるところまで頭が回らなかったような感じ
がする。自分で時間を取ってゆっくり考えたい。
• 頭が追いついていくのが精一杯でした。はやく出来
るようになって点数を見ても怖くならないようにし
たいです。又，ずっと前から知りたかった偏差値の
出し方が分かったので気持ち良かったです。（後略）

7. データの質
• I have been in Shizuoka for 6 years.
• a) been/for/I/six/Shizuoka/have/years/in
• b) be/for/I/six/Shizuoka/have/years/in: 動詞を正し
く活用させて

8. データの質
• 妥当性（validity）: 例.「恋愛力」測定
• 構成的妥当性: 恋愛力？, 人懐っこさ？or 自己中…？
• Cf. Rubin, Z. (1970) Measurement of romantic love.
• 概念的定義: 性質を記述 a) affiliative and
dependent need, b) a predisposition to help, and c)
an orientation of exclusiveness and absorption
• 操作的定義: 測定方法 The 13-item love-scale scores

9. データの質
• 妥当性（validity）: 例.「恋愛力」測定
• 構成的妥当性: 恋愛力？, 人懐っこさ？or 自己中…？
• 内容的妥当性: 告白まで？交際中？
• 基準関連妥当性
• 予測的: この人は「恋愛力」が高いから……♡
• 同時的: 別の測定法と比べると…

10. データの質
• 信頼性（reliability）: 安定して（ゆらぎなく）測れ
ているかどうか
• 検査・再検査、採点者内: 時間的
• 採点者間、平行検査: 空間的
• 内的整合性
• Cronbach’s alpha＞.80 or 折半法

11. 「妥当性」for what?
• a) データの一般化の可能性: 平均的な対象の行動を
収集データがどれだけ代表しているかということ
• b) 再使用性: 後になっても再検証できるようになっ
ていること
• c) 確証性: 同じ結果を確認できること
• Cf. 客観性・再現性・普遍性

12. 「妥当性」for what?
• 仮説検証型リサーチ; 実験の処理効果と実験結果
の因果関係・共起関係を示せるか
• 仮説生成型リサーチ; 現象をきちんと確認してい
ること、データの解釈に個人の主観的判断が入
り込んでいないことを証明できるか

13. 「妥当性」for what?
• 仮説検証型リサーチ; 実験の処理効果と実験結果
の因果関係・共起関係を示せるか
• 独立変数: 予測因子、研究者が操作する要因・現象
• 従属変数: 予測される方の変数、変化を測られる手段
• その他の変数: 被験者変数、外部変数

14. 恋人へのプレゼントに対するリターン
で恋愛力を測る
• バレンタイン・チョコ
• ホワイトデーのお返し
• 恋人の経済状態・育ち・好み
• チョコの予算
• 恋のライバル
• 恋人の友人の状況

15. 恋人へのプレゼントに対するリターン
で恋愛力を測る
• バレンタイン・チョコ（独立変数）
• ホワイトデーのお返し（従属変数）
• 恋人の経済状態・育ち・好み
• チョコの予算
• 恋のライバル
• 恋人の友人の状況

16. 予算
!
!
!
恋人の経済状態
好み・育ち
恋人へのプレゼントに対するリターン
で恋愛力を測る
バレンタイン
・チョコ
￥3,000
ホワイトデー
のお返し
￥9,000
友人の状況
ライバルの行動ライバルの行動ライバルの行動
Y=3X?

17. Task 1

18. Task 1
• いまこの教室には…
• リサーチメソッド受講者: ＿＿名
• このメンバーが所属する上位の集合を周り
の人と相談しながら考えてみよう

19. Task 1
• 英語教育リサーチメソッド受講者
• …静岡大学教育学部生
• …静岡大学生
• …静岡の大学生…日本の大学生
• …日本居住者（…地球人…知的生命体…）

20. 推測統計の考え方
• 背後の世界を推測するということ
• 手元のデータをこえて「一般的にはどうなのか」
• 母集団: 関心のある対象全体のこと
• 全数（悉皆）調査: 関心のある対象全体＝母集団
について調べ尽くすこと
• 母集団の大きさ: 母集団の構成要素の数 N

21. 推測統計の考え方
• 背後の世界を推測するということ
• 手元のデータをこえて「一般的にはどうなのか」
• 標本（サンプル）: 母集団の一部であり、実際に調査・
実験をした集団
• 標本（抽出）調査: 実際に手元に得られた標本から、
母集団の様子を推測する調査
• 標本の大きさ: 標本に含まれる要素の数 n

22. 推測統計の考え方
• 背後の世界を推測するということ
• 手元のデータをこえて「一般的にはどうなのか」
• 母集団: 関心のある対象全体のこと
• 標本（サンプル）: 母集団の一部であり、実際に調査・
実験をした集団
• （単純）無作為抽出: 母集団のどの要素についても等
しい確率で選ぶ標本抽出

23. 推測統計の考え方
• 英語教育リサーチメソッド受講者
• …静岡大学教育学部生（の代表と言える？）
• …静岡大学生（の代表と言える？）
• …静岡の大学生（の代表と言える？）
• …日本の大学生（の代表と言える？）
• …日本居住者（の代表と言える？）

24. - 2 -
→ :
:
! :
! : N
:
! :
! : n
:
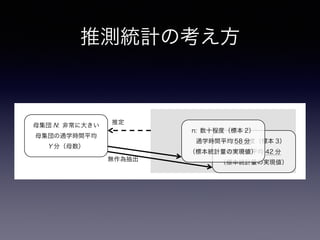
n: 数十程度（標本 3）
通学時間平均 42 分
（標本統計量の実現値）
母集団 N: 非常に大きい
母集団の通学時間平均
Y 分（母数）
無作為抽出
推定
推測統計の考え方

25. 推測統計の考え方
- 2 -
→ :
:
! :
! : N
:
! :
! : n
:
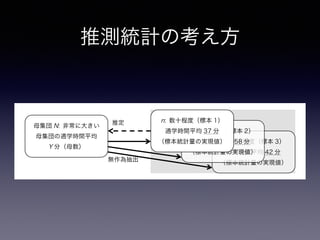
n: 数十程度（標本 3）
通学時間平均 42 分
（標本統計量の実現値）
n: 数十程度（標本 2）
通学時間平均 58 分
（標本統計量の実現値）
母集団 N: 非常に大きい
母集団の通学時間平均
Y 分（母数）
無作為抽出
推定

26. 推測統計の考え方
- 2 -
→ :
:
! :
! : N
:
! :
! : n
:
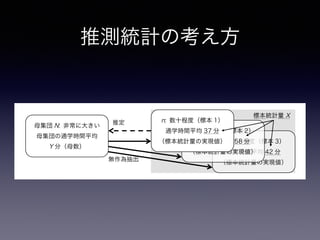
n: 数十程度（標本 3）
通学時間平均 42 分
（標本統計量の実現値）
n: 数十程度（標本 2）
通学時間平均 58 分
（標本統計量の実現値）
母集団 N: 非常に大きい
母集団の通学時間平均
Y 分（母数）
n: 数十程度（標本 1）
通学時間平均 37 分
（標本統計量の実現値）
無作為抽出
推定

27. 推測統計の考え方
- 2 -
→ :
:
! :
! : N
:
! :
! : n
:
n: 数十程度（標本 3）
通学時間平均 42 分
（標本統計量の実現値）
n: 数十程度（標本 2）
通学時間平均 58 分
（標本統計量の実現値）
母集団 N: 非常に大きい
母集団の通学時間平均
Y 分（母数）
n: 数十程度（標本 1）
通学時間平均 37 分
（標本統計量の実現値）
無作為抽出
推定
標本統計量 X

28. Task 2

29. Task 2
• Q1. サイコロ1つを1回振ったときに出
る目の数とその確率は…
確率変数の取る値 1 2 3 4 5 6
確率

30. Task 2
• Q1. サイコロ1つを1回振ったときに出
る目の数とその確率は…
確率変数の取る値 1 2 3 4 5 6
確率 1/6 1/6 1/6 1/6 1/6 1/6

31. Task 2
•P(α X β)＝(β­α) p
•P(2 X 5)＝(5­2) 1/6=0.5
確率変数の取る値 1 2 3 4 5 6
確率 1/6 1/6 1/6 1/6 1/6 1/6

32. Task 2
• 一様分布: どこをとっても一様に同じ
確率の分布

33. Task 2
• Q2. サイコロ2つを1回振ったときに出
た目の平均とその確率は…
確率変数
の取る値
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
確率

34. Task 2
• Q2. サイコロ2つを1回振ったときに出
た目の平均とその確率は…
確率変数
の取る値
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
組合わせ 1 2 3 4 5 6 5 4 3 2 1
確率
1/
36
1/
18
1/
12
1/
9
5/
36
1/
6
5/
36
1/
9
1/
12
1/
18
1/
36

35. Task 2
• 正規分布: 左右対称・釣り鐘型の性質
をもつ分布
確率変数
の取る値
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
組合わせ 1 2 3 4 5 6 5 4 3 2 1
確率
1/
36
1/
18
1/
12
1/
9
5/
36
1/
6
5/
36
1/
9
1/
12
1/
18
1/
36

36. Task 2
• 正規分布: 左右対称・釣り鐘型の性質
をもつ分布
確率変数
の取る値
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
組合わせ 1 2 3 4 5 6 5 4 3 2 1
確率
1/
36
1/
18
1/
12
1/
9
5/
36
1/
6
5/
36
1/
9
1/
12
1/
18
1/
360"
0.02"
0.04"
0.06"
0.08"
0.1"
0.12"
0.14"
0.16"
0.18"
1" 1.5" 2" 2.5" 3" 3.5" 4" 4.5" 5" 5.5" 6"

37. 母集団分布の仮定・推測
• 背後の世界を推測するということ
• 手元のデータをこえて「一般的にはどうなのか」
• 母集団: 関心のある対象全体のこと
• 標本（サンプル）: 母集団の一部であり、実際に調査・
実験をした集団
• （単純）無作為抽出: 母集団のどの要素についても等
しい確率で選ぶ標本抽出

38. 母集団分布の仮定・推測
• Q3. 大学生の恋愛感情得点（3∼15）の確率は
どの分布になる？
• 一様分布: どこも一様に同じ確率の分布
• 正規分布: 左右対称・釣り鐘型の性質をもつ分布
• 標準正規分布: 平均0、分散1の正規分布
• 非正規分布: 一様分布でも正規分布でもない

39. 母集団分布の仮定・推測
• Q3. 大学生の恋愛感情得点（3∼15）の確率は
どの分布になる？
• 一様分布: どこも一様に同じ確率の分布
• 正規分布: 左右対称・釣り鐘型の性質をもつ分布
• 標準正規分布: 平均0、分散1の正規分布
• 非正規分布: 一様分布でも正規分布でもない
0" 0" 0" 0" 0"
2"
4"
2"
3"
1"
5"
1"
2"
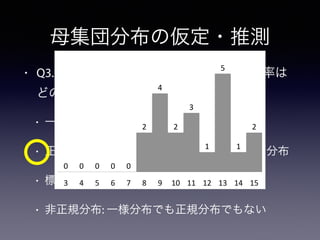
3" 4" 5" 6" 7" 8" 9" 10" 11" 12" 13" 14" 15"

40. 母集団分布の仮定・推測
• Q3. 大学生の恋愛感情得点（3∼15）の確率は
どの分布になる？
• 一様分布: どこも一様に同じ確率の分布
• 正規分布: 左右対称・釣り鐘型の性質をもつ分布
• 標準正規分布: 平均0、分散1の正規分布
• 非正規分布: 一様分布でも正規分布でもない
0" 0" 0" 0" 0"
2"
4"
2"
3"
1"
5"
1"
2"
3" 4" 5" 6" 7" 8" 9" 10" 11" 12" 13" 14" 15"
0" 0" 0" 0" 0"
1"
3"
1"
9"
14"
4"
3"
0"
3" 4" 5" 6" 7" 8" 9" 10" 11" 12" 13" 14" 15"
2013年度
n = 35

41. 母集団分布の仮定・推測
• Q3. 大学生の恋愛感情得点（3∼15）の確率は
どの分布になる？
• 一様分布: どこをとっても一様に同じ確率の分布
• 正規分布: 左右対称・釣り鐘型の性質
• e.g. 恋愛感情得点: 平均11.30、分散4.81
• 標準正規分布: 平均0、分散1の正規分布

42. 母集団分布の仮定・推測
• 確率変数Xの確率分布が正規分布N (μ, σ2
)であるとき: X~ N
(μ, σ2
)
• 恋愛感情得点X~ N (11.30, 4.81)
• 母集団に正規分布を仮定→標本平均の標本分布も正規分布
• 標本平均の分布の平均μx=母平均μ
• 標本分布の分散 σx
2
=σ2
/n

43. 母集団分布の仮定・推測
• X~ N (μ, σ2
)
• 母集団に正規分布を仮定→標本平均の標本分布も正規分布
• 標本分布の分散 σx
2
=σ2
/n: 4.81/20=0.2405
• 標準誤差（SE）: σ/√n: 2.19/√20=0.4904...
• 標本統計量の変動の大きさを評価する指標
• 母数について推測するときの精度

44. 母集団分布の仮定・推測
• X~ N (μ, σ2
)
• 標準誤差（standard error, SE）: σ/√n
• 標本分布の標準化:
• X ̅~ N (μ, σ2
/n)
• Z=(X ̅−μ)/σ⁄√n → Z~ N (0, 12
)
• ≒データの値−平均/標準偏差(σ)

45. 母集団分布の仮定・推測
• Q4. サイコロを１回投げて出た目の10倍のお金がも
らえるゲーム。参加料30円。参加した方が得だろ
うか？
• 期待値
• 確率×確率変数の総和
• 10×1/6+20×1/6+1/6×30+40×1/6+50×1/6+60×1/6=
210×1/6=35

46. 母集団分布の仮定・推測
• Q5. 世界中で今この瞬間トイレにいる人は何人？
• 1回あたり何分？1日何回？: 3分/回×3回=約10分
• →一日の10/60×24はトイレにいると仮定
• →世界中の全ての人が一日10/60×24はトイレで過
ごすと仮定
• 70億×10/60×24 = 48,611,111 ≒ 約4800∼4900万人

47. 母集団分布の仮定・推測
• Q6. セノバにある映画館（10シアター，1941席）の
年間売上はいくらでしょうか？
• 年間売上＝一日の売上×365日
• 土日と平日の差を考慮
• 年間売上＝平日の売上×250日+休日の売上×100日

48. 母集団分布の仮定・推測
• Q6. セノバにある映画館（10シアター，1941席）の年
間売上はいくらでしょうか？
• 一日の売上＝客単価×客数
• 客単価＝2000円と仮定
• チケット1500円
• 飲み物やパンフ代平均500円

49. 母集団分布の仮定・推測
• Q6. セノバにある映画館（10シアター，1941席）の年間売上
はいくらでしょうか？
• 一日の売上＝客単価(2000)×客数
• 客数＝最大集客人数×稼働率
• 最大集客人数＝席数(76∼320)×シアター数(10)×ターム数
(一日5ターム)＝9705人
• 稼働率: 平日10%、休日50%と仮定

50. 母集団分布の仮定・推測
• Q6. セノバにある映画館（10シアター，1941席）の年
間売上はいくらでしょうか？
• 年間売上＝平日の売上×250日+休日の売上×100日
• 一日の売上＝客単価(2000)×客数(9705(平日10%, 休日
50%))
• 9705人×2000円×10%×250日+9705人×2000円
×50%×100日＝1455750000 ≒ 14∼15億程度

51. 母集団分布の仮定・推測
• 推定量: 母数の推定に用いられる標本統計量
• 標本平均X ̅（→母集団平均μ）
• 標本比率p（→母集団比率π）
• 標本相関係数r（→母集団相関係数ρ）
• 点推定: １つの値を用いて母数を推定
• 区間推定: ある一定の区間を設けて、母数の推定を区間でおこな
うこと

52. 母集団分布の仮定・推測
• 推定量: 母数の推定に用いられる標本統計量
• 不偏性がある: 推定量の期待値と母数の差（偏り）が0
• 95%信頼区間: p−1.96σp ≦ π ≦ p+1.96σp
• 標本抽出を繰返す度に信頼区間を求めると全体の95
％は母数πを含む区間になる
• 例. 恋愛感情得点: 11.30±1.96×0.49 = 95% CI [10.34, 12.26]

53. 母集団分布の仮定・推測
• 推定量: 母数の推定に用いられる標本統計量
• 母集団が何であっても
• 1) 標本平均の期待値は母平均に一致
• 2) 標準誤差＝σ/√n

54. 統計的仮説検定の手順
• 考え方・論理は…
• 「Aだ！」というのではなく、
• 「Not Aではない（のだからAだ！）」、
• 「Not Aの可能性は限りなく低い（から、Aで
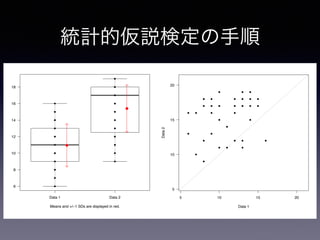
あると判断できるのではないか）」

55. 統計的仮説検定の手順
• [手順１] 仮説を設定する
• 帰無仮説: 棄却される(不支持になる)ことを目的に作られる仮説
• 対立仮説: 帰無仮説が棄却されたときに採択される仮説
• 両側検定: 差がある、方向は問わない
• 片側検定: 差・方向性がある
• どちらかをこの時点で（データをとる前に）決定

56. 統計的仮説検定の手順
• [手順１] 仮説を設定する
• 帰無仮説: 例. 小テストに口頭試験を導入しても、生徒のスピーキ
ング能力に変化はない。
• 対立仮説: 例. 小テストに口頭試験を導入すると、生徒のスピー
キング能力に変化がある。
• 両側検定:
• 帰無仮説H0：生徒のスピーキング能力の変化=0
• 対立仮説H1：生徒のスピーキング能力の変化≠0

57. 統計的仮説検定の手順
• [手順２] 統計的検定に用いられる標本統計量を選択
する
• 検定統計量: 検定をおこなうために標本から計算
される標本統計量
• 例: Z得点: Z=(X ̅−μ)/σ⁄√n
• 例: 1回目と3回目のスピーキング能力の差 → T得点

58. 統計的仮説検定の手順
• [手順３] 仮説が間違っているか正しいかの判断の基
準になる確率を設定する
• 有意水準: どの程度低い確率の結果が示されたら帰無
仮説を棄却するかという基準α
• α = 0.05 (5%)かα = 0.01 (1%)での設定が一般的
• 臨界値: 帰無仮説を棄却し対立仮説を採択するという
境目になる値

59. 統計的仮説検定の手順
• [手順３] 仮説が間違っているか正しいかの判断の基準に
なる確率を設定する
• 棄却域: 帰無仮説のもとでの標本分布で、その確率がαと
なる領域
• 両側検定α = 0.05: Z ≦ −1.96 or 1.96 ≦ Z
• 片側検定α = 0.05: 1.645 ≦ Z
• 採択域: 帰無仮説を採択することになる領域

60. 統計的仮説検定の手順
• [手順３] 仮説が間違っているか正しいかの判断の基準に
なる確率を設定する
• 棄却域: 帰無仮説のもとでの標本分布で、その確率がαと
なる領域
• 両側検定α = 0.05: t(39) ≦ −2.0227 or 2.0227 ≦ t(39)
• 片側検定α = 0.05: 1.6849 ≦ t(39)
• 採択域: 帰無仮説を採択することになる領域

61. 統計的仮説検定の手順
Data 1 Data 2
6
8
10
12
14
16
18
Means and +/−1 SDs are displayed in red.
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●●
●
●●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●●
●
●
●●
●
●
● ●
●
● ● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●●
●
●
● ●
●
5 10 15 20
5
10
15
20
Data 1
Data2

62. 統計的仮説検定の手順
• [手順４] 実際のデータから標本統計量の実現値を計
算する
• 例. Z=(X ̅−μ)/σ⁄√n
• 仮に...大学生の恋愛感情得点
• 平均: 10.5、分散: 9
• Z = (11.30−10.5)/3/√20 = 1.192569588...

63. 統計的仮説検定の手順
• [手順５] 最初に定めた仮説が間違っているか正しい
かを判断する
• 検定統計量の実現値が
• 棄却域に入る: 帰無仮説を棄却する
• 「5％水準で有意である」
• 「p ＜ .05」

64. 統計的仮説検定の手順
• [手順５] 最初に定めた仮説が間違っているか正し
いかを判断する
• 検定統計量の実現値が
• 棄却域に入らない: 帰無仮説を採択
• 「有意な差は認められなかった」
• 「n.s.」

65. 統計的仮説検定における
2種類の誤り
真実
決定 H H
H
第1種の誤り
確率α
正しい決定
確率1−β: 検定力
H
正しい決定
確率1−α
第2種の誤り
確率β

66. 浮気が気になるゥ！の
2種類の誤り
真実
決定 浮気してない 浮気した
愛情変化あり
第1種の誤り
勘違いヤロー
正しい決定
確率1−β: 検定力
愛情変化なし
正しい決定
確率1−α
第2種の誤り
鈍感ボーイ

67. Task 3
• 母分散σ2が既知の場合の１つの平均値の検定
• Q. See p.5: 平均50点、分散144の正規分布を
示す県の模試をクラスの生徒25人が受けた
ところ、平均点は53点。このクラスは県内
平均より成績が良いと言えるか（有意水準5
％片側検定）

68. 課題３
• Task 3について、手順に沿って検定を実行し、その
過程と結果を記述
• A大学１年生42名の2013TOEICスコア（LiveCampusま
たはFBからダウンロード）。第187回TOEIC公式デー
タ（リンクはDLファイルを参照）に照らして有意な
差があるかどうか検定（有意水準5％両側検定）
• 5月7日午前1時まで、LiveCampusを通じて提出