More Related Content
PDF
PDF
PPTX
20110219setsumeiken tomida PPTX
Jap2017 ss65 優しいベイズ統計への導入法 PDF
PDF
プレゼンの成果を決める、スライド作成のテクニックとルール(基礎編) 先生:山口 周 PDF
PDF
Similar to 2017年度 夏季統計ゼミ 08.24
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
第8回山口県英語教育フォーラム(亘理スライド公開版) PDF
PDF
PDF
PDF
PDF
PDF
2017年度 夏季統計ゼミ 08.24
- 1.
- 2.
- 3.
- 4.
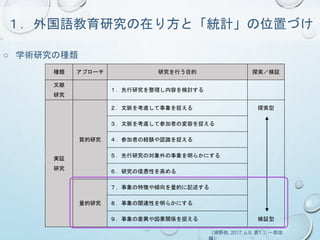
1.外国語教育研究の在り方と「統計」の位置づけ
○ 学術研究の種類
種類 アプローチ研究を行う目的 探索/検証
文献
研究
1.先行研究を整理し内容を検討する
実証
研究
質的研究
2.文脈を考慮して事象を捉える 探索型
3.文脈を考慮して参加者の変容を捉える
4.参加者の経験や認識を捉える
5.先行研究の対象外の事象を明らかにする
6.研究の信憑性を高める
量的研究
7.事象の特徴や傾向を量的に記述する
8.事象の関連性を明らかにする
9.事象の差異や因果関係を捉える 検証型
(浦野他, 2017, p.8, 表1.1; 一部改
- 5.
1.外国語教育研究の在り方と「統計」の位置づけ
○ データの収集法による分類
・ 事例研究
例:授業のICT化の効果を明らかにするために、生徒が1人1台タブ
レット PCを持っている学校の英語の授業を3ヶ月間参観し、記
録しました。
・ 調査研究
例: 語彙サイズと文法処理速度の関係が知りたいので、たくさんの大
学生 に語彙サイズテストとSPSTを受けてもらいました。
・ 実験研究
例: 高校生がどのくらい速読をしたらwpmが向上するのかを明らかに
する ため、実験群と統制群を設けて指導中のwpmの変化をそれ
ぞれ測定 しました。
- 6.
○ 外国語教育研究における論文の基本的な構成
(1) Introduction
(2)Background
(3) Research Design
(4) Result
(5) Discussion
(6) Conclusion
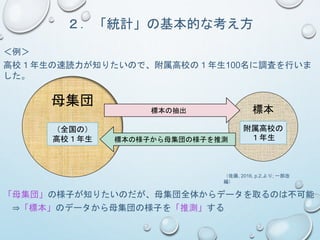
2.「統計」の基本的な考え方
渋谷さん
「統計を使うのはデータ分析の時だから、分析方法はあとから考えればいい
や。」
分析方法によって必要なデータの種類が異なる
(=取ったデータの種類によって使える分析が異なる)
⇒データ収集の前に分析方法まで考えておく必要がある
データを
取る前
データを
取った後
←統計を使うのはココ
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
演習問題①
① まず、raw dataを見てみる
②「基本統計量」と「ヒストグラム」を出す
⇒ 結果を見て、 「3人の先生たちの意見に賛同できるか」をディスカッ
ションして ください
⇒ 3人の先生たちに賛同できるかどうか、それぞれ○・△・×で答えてくだ
さい。
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
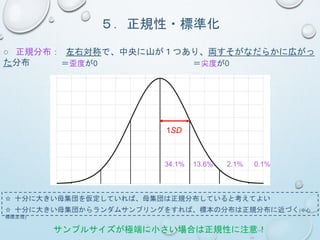
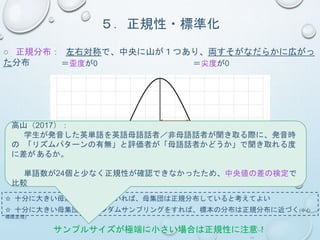
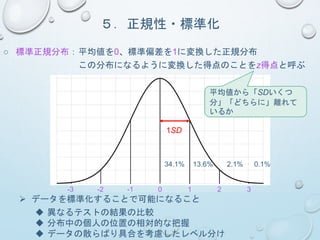
5.正規性・標準化
○ 正規分布: 左右対称で、中央に山が1つあり、両すそがなだらかに広がっ
た分布=歪度が0 =尖度が0
1SD
34.1% 13.6% 2.1% 0.1%
☆ 十分に大きい母集団を仮定していれば、母集団は正規分布していると考えてよい
☆ 十分に大きい母集団からランダムサンプリングをすれば、標本の分布は正規分布に近づく(中心
極限定理)
サンプルサイズが極端に小さい場合は正規性に注意!
高山(2017):
学生が発音した英単語を英語母語話者/非母語話者が聞き取る際に、発音時
の 「リズムパターンの有無」と評価者が「母語話者かどうか」で聞き取れる度
に差があるか。
単語数が24個と少なく正規性が確認できなかったため、中央値の差の検定で
比較
- 20.
- 21.
- 22.
演習問題②
① まず、raw dataを見てみる
②「相関係数」と「プロット」を出す(時間があれば「基本統計量」と「ヒ
ストグラム」も)
⇒ 結果を見て、 八丁畷さんの仮説が正しいかをディスカッションしてく
ださい
⇒ それぞれの仮説に賛同できるかどうか、○・△・×で答えてください。
- 23.
演習問題② 補足
① まず、rawdataを見てみる
② 「相関係数」と「プロット」を出す(時間があれば「基本統計量」と「ヒ
ストグラム」も)
⇒ 結果を見て、 八丁畷さんの仮説が正しいかをディスカッションしてく
ださい
⇒ それぞれの仮説に賛同できるかどうか、○・△・×で答えてください。
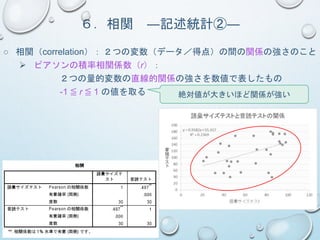
語彙力と音読速度:「大学生よりも高校生のほうが関係が強いか?」
大学生:r=.481 高校生: r=.531
「語彙力は音読の正確性に影響しているか」
相関係数は r=.491 (中程度の正の相関)
- 24.
演習問題② 補足
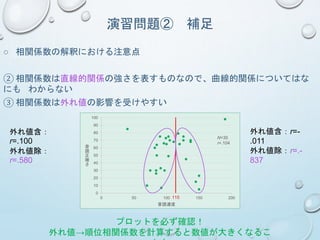
○ 相関係数の解釈における注意点
①相関関係は関係の強さを表すものなので、変数間の因果関係はわからない
相関係数の値から変数同士の関係性を解釈するのは研究者次第
「語彙力が音読速度/正確性に影響している」と言えるか??
偏相関の可能性(第3の変数)
例: ワーキングメモリの大きさが「語彙力」と「音読速度」にそれ
ぞれ影響 しており、 「語彙力」と「音読速度」の間には因果
関係はない
- 25.
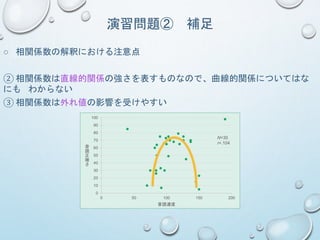
演習問題② 補足
○ 相関係数の解釈における注意点
②相関係数は直線的関係の強さを表すものなので、曲線的関係についてはな
にも わからない
③ 相関係数は外れ値の影響を受けやすい
0
10
20
30
40
50
60
70
80
90
100
0 50 100 150 200
音
読
正
確
さ
音読速度
N=30
r=.104
- 26.
演習問題② 補足
○ 相関係数の解釈における注意点
②相関係数は直線的関係の強さを表すものなので、曲線的関係についてはな
にも わからない
③ 相関係数は外れ値の影響を受けやすい
0
10
20
30
40
50
60
70
80
90
100
0 50 100 150 200
音
読
正
確
さ
音読速度
115
N=30
r=.104
外れ値含:
r=.100
外れ値除:
r=.580
外れ値含:r=-
.011
外れ値除:r=.-
837
プロットを必ず確認!
外れ値→順位相関係数を計算すると数値が大きくなるこ
- 27.
演習問題② 補足
○ 相関係数の解釈における注意点
④相関係数は標本の大きさの影響を受けやすい
N=2の場合、必ずr=1かr=-1になる
だからといってたくさんデータを取ればいいわけではない
有意性の解釈は特に慎重に(有意確率よりもrの値を重視)
⑤ 相関係数は順序尺度である
数値の大小は、関係の強さの大小を表す
r=.20とr=.40では、後者の方が関係が強い。ただし、関係の強さが2倍
であるとは言えない
- 28.
演習問題② 補足
○ 相関係数の解釈における注意点
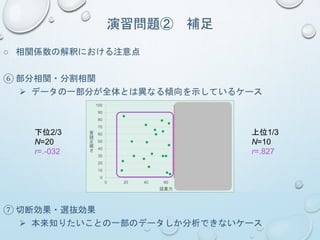
⑥部分相関・分割相関
データの一部分が全体とは異なる傾向を示しているケース
⑦ 切断効果・選抜効果
本来知りたいことの一部のデータしか分析できないケース
0
10
20
30
40
50
60
70
80
90
100
0 20 40 60 80 100 120
音
読
正
確
さ
語彙力
N=30
r=.491
下位2/3
N=20
r=.-032
上位1/3
N=10
r=.827
- 29.
演習問題② 補足
○ 決定係数(𝑟2)
相関係数(r)の値を二乗した数値
p.8の例題では、𝑟2=0.487×0.487=0.237
「音読速度の変動の23.7%を語彙力の変動で説明できる」(もしく
は逆)
=音読速度が変化した理由の23.7%は語彙力の変化である
𝑟2は比例尺度。𝑟2=.04と𝑟2=.16では後者のほうが4倍説明力が高いと言
える
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
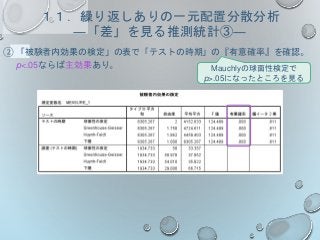
演習問題③ 解答
【A】
① 自分の体温(℃):間隔尺度その日の歩数:比例尺度
② 留学の前後:名義尺度 TOEFLの点数:間隔尺度
③ 英検の級:順序尺度 TOEICの点数:間隔尺度
④ その日の飲酒量:比例尺度 発話語数:比例尺度
⑤ 小学校英語を受けたかどうか:名義尺度 小学校英語への賛否:名義尺度
- 37.
演習問題③ 解答
【B】 𝐻0:留学の前後TOEFLの点数の平均値に差がない
𝐻1:留学の前後TOEFLの点数の平均値に差がある
○推測統計を行った結果、「p=.045」という結果でした。
これは、帰無仮説が正しいと仮定した時に今回のようなデータが得られる
確率が 4.5%であることを意味しています。
○ このpのことを有意確率と呼びます。
pの値は有意水準よりも低いので、帰無仮説を棄却して対立仮説を採択しま
す。
○ 留学前のTOEFLの平均点は535点で、留学後のTOEFLの平均点は709点でし
た。したがって、留学の前後でTOEFLの平均点には有意な差があり、留学
前と比 べて留学後のTOEFLの点数は上昇しているといえます。
もしも留学前のTOEFLの平均点が709点で留学後のTOEFLの平均点が535点
- 38.
- 39.
- 40.
- 41.
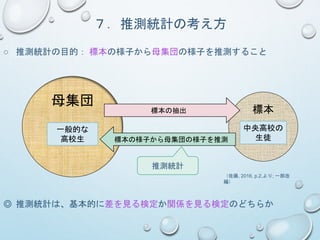
【A】空欄を埋めましょう。
① 推測統計ではまず[ ](𝐻0)と[](𝐻1)を立
てる。𝐻0は差・関係 が[ ]という仮説、𝐻1は差・関係が[ ]と
いう仮説である。
② 帰無仮説が正しいと仮定した場合に標本のようなデータが得られる確率を
[ ( )]という。この確率が[ ( )]より
も小さければ、帰無仮説を [ ]して対立仮説を[ ]する。つま
り、差や関係が[ ]という結果になる。
③ 反対に有意確率が有意水準よりも大きければ、帰無仮説を[ ]す
る。
つまり、差や関係が[ ]という結果になる。
外国語教育研究では、通例有意水準を[ ]%に設定する。
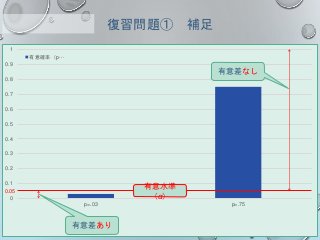
復習問題①
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
演習問題④
① まず、raw dataを見て結果の予測を立てる
②SPSSで対応ありのt検定を行う
③ (時間があれば「相関係数」「プロット」 「基本統計量」「ヒストグラ
ム」を出す)
⇒ 結果を見て、 宝積寺さんの仮説が正しいかをディスカッションしてく
ださい
⇒ 宝積寺さんの仮説に賛同できるかどうか、○・△・×で答えてください。
- 55.
演習問題④ 補足
① まず、rawdataを見て結果の予測を立てる
② SPSSで対応ありのt検定を行う
③ (時間があれば「相関係数」「プロット」 「基本統計量」「ヒストグラ
ム」を出す)
⇒ 結果を見て、 宝積寺さんの仮説が正しいかをディスカッションしてく
ださい
⇒ 宝積寺さんの仮説に賛同できるかどうか、○・△・×で答えてください。
フォニックス指導によって英単語を正しく書き取ることができるように
なったか?
統計的には有意な差があった(プレ<ポスト)
- 56.
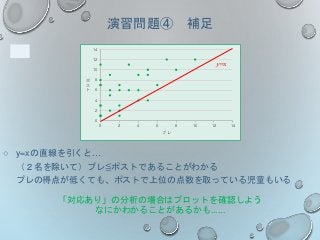
演習問題④ 補足
0
2
4
6
8
10
12
14
0 24 6 8 10 12 14
ポ
ス
ト
プレ
y=x
○ y=xの直線を引くと…
(2名を除いて)プレ≦ポストであることがわかる
プレの得点が低くても、ポストで上位の点数を取っている児童もいる
「対応あり」の分析の場合はプロットを確認しよう
なにかわかることがあるかも......
- 57.
- 58.
- 59.
- 60.
演習問題⑤
① まず、raw dataを見て結果の予測を立てる
②SPSSで対応なしのt検定を行う
③ (時間があれば 「基本統計量」「ヒストグラム」を出す)
⇒ 結果を見て、 広さんの研究結果についてディスカッションしてくださ
い
⇒ 「パラレルリーディングのほうが効果がある」
「シャドーイングのほうが効果がある」
「どちらともいえない」 で答えてください。
- 61.
演習問題⑤ 補足
① まず、rawdataを見て結果の予測を立てる
② SPSSで対応なしのt検定を行う
③ (時間があれば 「基本統計量」「ヒストグラム」を出す)
⇒ 結果を見て、 広さんの研究結果についてディスカッションしてくださ
い
⇒ 「パラレルリーディングのほうが効果がある」
「シャドーイングのほうが効果がある」
「どちらともいえない」 で答えてください。
パラレルリーディングとシャドーイングのどちらが効果があるか?
統計的に有意な差はなかった
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
演習問題⑥
① まず、raw dataを見て結果の予測を立てる
②SPSSで繰り返しありの一元配置分散分析を行う
③ (時間があれば「相関係数」「プロット」 「基本統計量」「ヒストグラ
ム」を出す)
⇒ 結果を見て、 ディクトグロスの効果があったといえるかどうかついて
ディスカッ ションしてください
⇒ ディクトグロスの効果があったといえるかどうか、○・△・×で答えてく
ださい。
- 68.
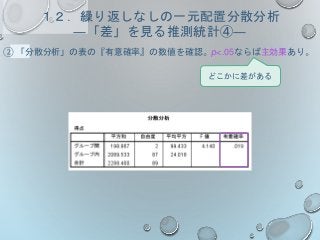
演習問題⑥ 補足
① まず、rawdataを見て結果の予測を立てる
② SPSSで繰り返しありの一元配置分散分析を行う
③ (時間があれば「相関係数」「プロット」 「基本統計量」「ヒストグラ
ム」を出す)
⇒ 結果を見て、 ディクトグロスの効果があったといえるかどうかついて
ディスカッ ションしてください
⇒ ディクトグロスの効果があったといえるかどうか、○・△・×で答えてく
ださい。
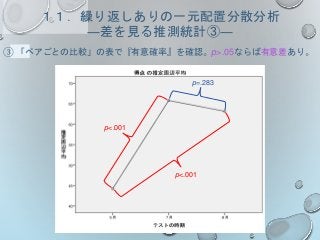
ディクトグロスの効果はあるか?
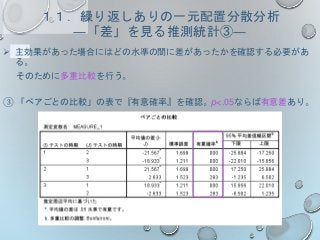
主効果があり、全てのテストの間で有意差があった
- 69.
0
10
20
30
40
50
60
70
80
90
100
0 10 2030 40 50 60 70 80 90 100
1月
9月
y=x
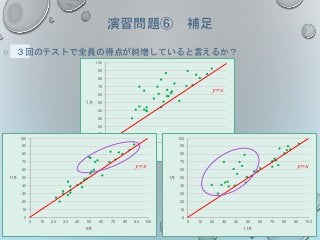
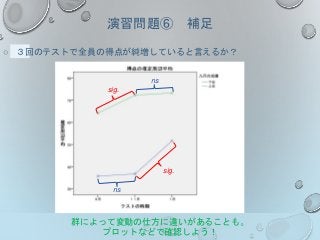
演習問題⑥ 補足
○ 3回のテストで全員の得点が純増していると言えるか?
0
10
20
30
40
50
60
70
80
90
100
0 10 20 30 40 50 60 70 80 90 100
11月
9月
y=x
0
10
20
30
40
50
60
70
80
90
100
0 10 20 30 40 50 60 70 80 90 100
1月
11月
y=x
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
演習問題⑦ 補足
① まず、rawdataを見て結果の予測を立てる
② SPSSで繰り返しなしの一元配置分散分析を行う
③ (時間があれば「基本統計量」「ヒストグラム」を出す)
⇒ 結果を見て、 それぞれの指導法の効果についてディスカッションして
ください
⇒ それぞれの指導法を効果があったと思う順に並べてください。
リキャストテストの得点に差はあるか?
主効果があり、「新冠クラス>占冠クラス」(それ以外は有意差な
し)という 結果であった
- 77.
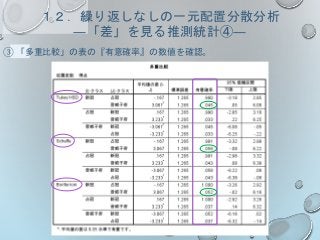
演習問題⑦ 補足
○ 論文への記載の仕方
3クラスのリキャストテストの得点を繰り返しなしの一元配置分散分析で
比較したところ、テスト得点の主効果が認められた( F(2, 87)=3.463,
MSE=23.740, p=.036 )
Tukey法による多重比較の結果、新冠クラスと占冠クラスの間に有意な差が
認め られた(p=.029)が、新冠クラスと音威子府クラスの間(p=.223)、占
冠クラスと音 威子府クラスの間(p=.625)には有意差がなかった。
☆ 他に、「分散分析表」という形で結果を載せる方法もある。
有意確率
F値
要因(グループ
間)
の自由度
誤差(グループ
内)
の平均平方
誤差(グループ
内)
の自由度
- 78.
- 79.
- 80.
- 81.
- 82.
- 83.
- 84.
- 85.
- 86.
- 87.
- 88.
- 89.
- 90.
- 91.
- 92.
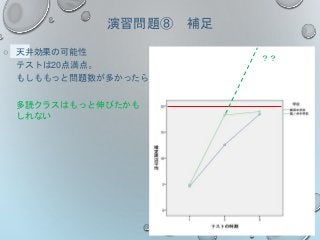
演習問題⑧ 補足
① まず、rawdataを見て結果の予測を立てる
② SPSSで二元配置分散分析(混合計画)を行う
⇒ 結果を見て、 それぞれの指導法の効果についてディスカッションして
ください
⇒ 「多読」と「語彙リスト」のどちらがより効果があると思うかを答えて
ください。
それぞれのクラスの得点はどのように変化した?
交互作用あり
指導法(学校)の主効果あり(飯田<篠ノ井)
時期の主効果あり(プレ<一ヵ月後<三ヵ月後)
- 93.
- 94.
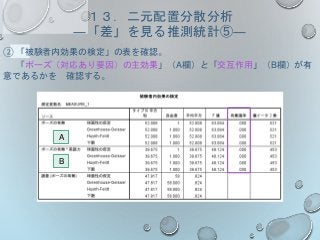
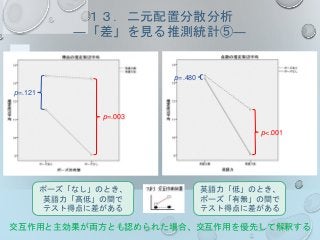
演習問題⑧ 補足
○ 論文への記載の仕方
「テストの時期」及び「指導法」を独立変数としてテストの得点について二元配置分散
分析を行ったところ有意な交互作用が認められ(F(1.613,93.554)=37.228, MSE=4.742,
p<.001; Greenhouse-Geisserにより調整)、テストの時期の主効果(F(1.613,
93.554)=836.700, MSE=4.742, p<.001; Greenhouse-Geisserにより調整)及び指導法
の主効果 (F(1, 58)=47.286, MSE=4.513, p<.001)がそれぞれ認められた。
Bonferroni法による単純主効果の検定の結果、語彙リストクラスにおいては全ての水準
間で有意な差があり(いずれもp<.001) 、多読クラスにおいてはプレと一月後及びプ
レと三月後の間でそれぞれ有意な差があった(いずれもp<.001)。
また、一月後のテストにおいて語彙リストクラスと多読クラスの間に有意な差があった
(p<.001)。
さらに時期の主効果についてBonferroni法による多重比較を行ったところ、全ての水準
間で有意な差が認められた(いずれもp<.001)。
- 95.
- 96.
- 97.
- 98.
- 99.
- 100.
- 101.
- 102.
- 103.
- 104.
- 105.
- 106.
- 107.
- 108.
- 109.
- 110.
- 111.
- 112.
- 113.
- 114.
- 115.
- 116.
- 117.
- 118.
- 119.
- 120.
- 121.
- 122.
- 123.
- 124.
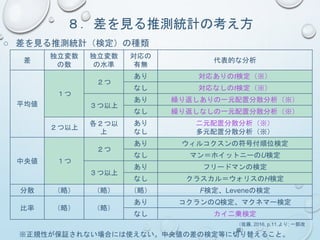
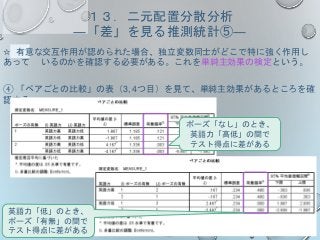
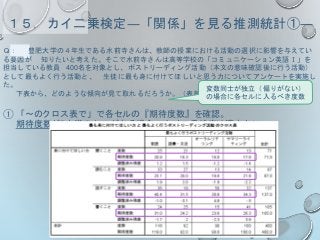
14.「関係」を見る推測統計の考え方
○ 関係を見る推測統計の種類
変数の数 変数の尺度代表的な分析
2つ
間隔・比例尺度同士
ピアソンの積率相関係数(※1)
単回帰分析(※1)
順序尺度同士
スピアマンの順位相関係数(ρ)
ケンドールの順位相関係数(τ)
名義尺度同士 カイ二乗検定
3つ以上 ― 【多変量解析】
※1:正規性が保証されない場合には使えない。順位相関係数を用いること。
(佐藤, 2016, p.11,より; 一部改
編)
- 125.
- 126.
- 127.
- 128.
- 129.
- 130.
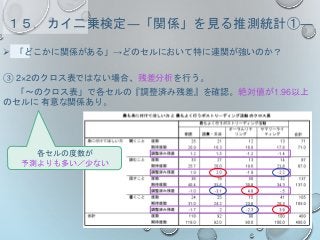
演習問題⑨ 補足
① まず、rawdataを見て結果の予測を立てる
② SPSSでカイ二乗検定を行う
⇒ 結果を見て、 校種と賛否の関係についてディスカッションしてくださ
い
⇒ 校種と賛否に関係があると言えると思うか、○・△・×で答えてくださ
い。
校種と賛否には関係があるか?
カイ二乗検定の結果、有意な関係あり
残差分析の結果、 小学校教員は「賛成」が多い
中学校教員は「どちらでもない」が少ない
高校教員は「賛成」が少なく、「どちらでもな
い」が多い
- 131.
- 132.
- 133.
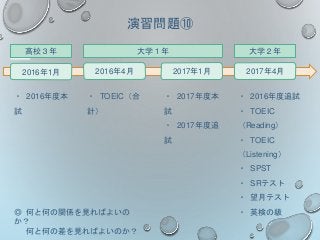
演習問題⑩
2016年1月 2016年4月 2017年1月2017年4月
高校3年 大学1年 大学2年
・ 2016年度本
試
・ TOEIC(合
計)
・ 2017年度本
試
・ 2017年度追
試
・ 2016年度追試
・ TOEIC
(Reading)
・ TOEIC
(Listening)
・ SPST
・ SRテスト
・ 望月テスト
・ 英検の級◎ 何と何の関係を見ればよいの
か?
何と何の差を見ればよいのか?
- 134.
- 135.
- 136.
- 137.
- 138.
- 139.
- 140.
- 141.
- 142.
- 143.
- 144.
- 145.
- 146.
- 147.
- 148.
- 149.
- 150.
- 151.
- 152.
- 153.
- 154.
- 155.
- 156.
- 157.
- 158.
- 159.
- 160.
- 161.
- 162.
- 163.
- 164.
- 165.
- 166.
- 167.
- 168.
- 169.
- 170.
- 171.
- 172.
- 173.
- 174.
- 175.
- 176.
- 177.
- 178.
- 179.
- 180.
- 181.
- 182.
- 183.
- 184.
- 185.
- 186.
- 187.
- 188.
- 189.
- 190.
- 191.
- 192.
- 193.







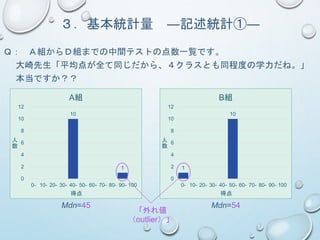
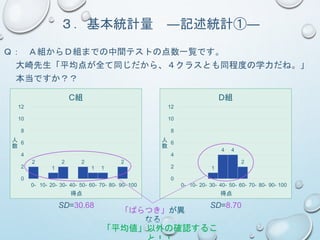









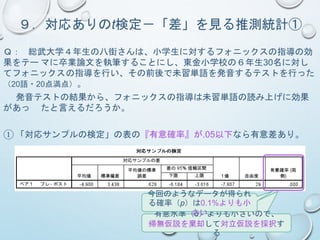
![7.推測統計の考え方
Q: 「演習問題①(p.5)で一般入試・推薦入試・内部進学で中央高校に入学
した生徒 の実力テストの平均点はそれぞれ次のとおりでした[一般:55.0、推
薦:55.5、 内部:60.0]。
したがって、一般的な高校生の英語力は『内部進学の生徒>推薦 入試で入
学し た生徒>一般入試で入学した生徒』だと言えます。」 本当ですか??
55.0
55.5
60.0
52
53
54
55
56
57
58
59
60
61
一般 推薦 内部
平
均
点
データを取ったのは中央高校の生徒の
み
「一般と推薦の平均点の差」(0.5点)
と 「推薦と内部の平均点の差」(4.5
点)は それぞれ本当に意味のある差
なのか?
直感的には…](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-30-320.jpg)






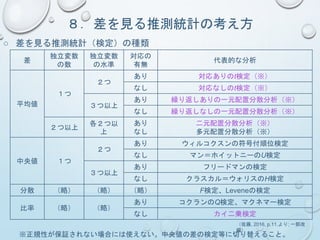
と[ ](𝐻1)を立
てる。𝐻0は差・関係 が[ ]という仮説、𝐻1は差・関係が[ ]と
いう仮説である。
② 帰無仮説が正しいと仮定した場合に標本のようなデータが得られる確率を
[ ( )]という。この確率が[ ( )]より
も小さければ、帰無仮説を [ ]して対立仮説を[ ]する。つま
り、差や関係が[ ]という結果になる。
③ 反対に有意確率が有意水準よりも大きければ、帰無仮説を[ ]す
る。
つまり、差や関係が[ ]という結果になる。
外国語教育研究では、通例有意水準を[ ]%に設定する。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-41-320.jpg)
と[対立仮説](𝐻1)を立てる。𝐻0
は差・関係 が[ない]という仮説、𝐻1は差・関係が[ある]という仮説であ
る。
② 帰無仮説が正しいと仮定した場合に標本のようなデータが得られる確率を
[ ( )]という。この確率が[ ( )]より
も小さければ、帰無仮説を [ ]して対立仮説を[ ]する。つま
り、差や関係が[ ]という結果になる。
③反対に有意確率が有意水準よりも大きければ、帰無仮説を[ ]する。
つまり、差や関係が[ ]という結果になる。
外国語教育研究では、通例有意水準を[ ]%に設定する。
④ 推測統計の結果、母集団において差があることを[ ]な差があると
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-42-320.jpg)
と[対立仮説](𝐻1)を立てる。𝐻0
は差・関係 が[ない]という仮説、𝐻1は差・関係が[ある]という仮説であ
る。
② 帰無仮説が正しいと仮定した場合に標本のようなデータが得られる確率を
[有意確率(p)]という。この確率が[有意水準(α)]よりも小さけれ
ば、帰無仮説を[棄却]して対立仮説を[採択]する。つまり、差や関係が
[ある]という結果になる。
③ 反対に有意確率が有意水準よりも大きければ、帰無仮説を[ ]す
る。
つまり、差や関係が[ ]という結果になる。
外国語教育研究では、通例有意水準を[ ]%に設定する。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-43-320.jpg)
と[対立仮説](𝐻1)を立てる。𝐻0
は差・関係 が[ない]という仮説、𝐻1は差・関係が[ある]という仮説であ
る。
② 帰無仮説が正しいと仮定した場合に標本のようなデータが得られる確率を
[有意確率(p)]という。この確率が[有意水準(α)]よりも小さけれ
ば、帰無仮説を[棄却]して対立仮説を[採択]する。つまり、差や関係が
[ある]という結果になる。
③ 反対に有意確率が有意水準よりも大きければ、帰無仮説を[採択]する。
つまり、差や関係が[ない]という結果になる。
外国語教育研究では、通例有意水準を[5]%に設定する。
④ 推測統計の結果、母集団において差があることを[ ]な差があると
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-44-320.jpg)
と[対立仮説](𝐻1)を立てる。𝐻0
は差・関係 が[ない]という仮説、𝐻1は差・関係が[ある]という仮説であ
る。
② 帰無仮説が正しいと仮定した場合に標本のようなデータが得られる確率を
[有意確率(p)]という。この確率が[有意水準(α)]よりも小さけれ
ば、帰無仮説を[棄却]して対立仮説を[採択]する。つまり、差や関係が
[ある]という結果になる。
③ 反対に有意確率が有意水準よりも大きければ、帰無仮説を[採択]する。
つまり、差や関係が[ない]という結果になる。
外国語教育研究では、通例有意水準を[5]%に設定する。
④ 推測統計の結果、母集団において差があることを[有意]な差があるとい
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-45-320.jpg)
![【B】「夏期講習の前後で実力テストの点数の平均値に差があるか」を明らか
に するための推測統計の手順です。空欄を埋めましょう。
○ 帰無仮説、対立仮説はそれぞれ
帰無仮説[𝐻0]:夏期講習の前後で実力テストの点数の平均値に
[ ]。
対立仮説[𝐻1]:夏期講習の前後で実力テストの点数の平均値に
[ ]。
です。
○ 独立変数は[ ]つあり、[ ]です([ ]水準)。
従属変数は[ ]つあり、[ ]です。
同じ人のデータを比較しているので、対応[ ]の分析になります。
したがって、[ ]という分析方法を用います。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-46-320.jpg)
![【B】「夏期講習の前後で実力テストの点数の平均値に差があるか」を明らか
に するための推測統計の手順です。空欄を埋めましょう。
○ 帰無仮説、対立仮説はそれぞれ
帰無仮説[𝐻0]:夏期講習の前後で実力テストの点数の平均値に[差がな
い]。
対立仮説[𝐻1]:夏期講習の前後で実力テストの点数の平均値に[差があ
る]。
です。
○ 独立変数は[ ]つあり、[ ]です([ ]水準)。
従属変数は[ ]つあり、[ ]です。
同じ人のデータを比較しているので、対応[ ]の分析になります。
したがって、[ ]という分析方法を用います。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-47-320.jpg)
![【B】「夏期講習の前後で実力テストの点数の平均値に差があるか」を明らか
に するための推測統計の手順です。空欄を埋めましょう。
○ 帰無仮説、対立仮説はそれぞれ
帰無仮説[𝐻0]:夏期講習の前後で実力テストの点数の平均値に[差がな
い]。
対立仮説[𝐻1]:夏期講習の前後で実力テストの点数の平均値に[差があ
る]。
です。
○ 独立変数は[1]つあり、[テストの時期]です([2]水準)。
従属変数は[1]つあり、[実力テストの点数]です。
同じ人のデータを比較しているので、対応[あり]の分析になります。
したがって、[対応ありのt検定]という分析方法を用います。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-48-320.jpg)
![【B】「夏期講習の前後で実力テストの点数の平均値に差があるか」を明らか
に するための推測統計の手順です。空欄を埋めましょう。
○ 推測統計を行った結果、「p=.083」という結果でした。
これは、[ ]が正しいと仮定した時に今回のようなデータが
得られる確率 が[ ]%であることを意味しています。
○ p値は有意水準よりも[ ]ので、[ ]を採択します。
つまり、有意な差は[ ]という結果になりました。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-49-320.jpg)
![【B】「夏期講習の前後で実力テストの点数の平均値に差があるか」を明らか
に するための推測統計の手順です。空欄を埋めましょう。
○ 推測統計を行った結果、「p=.083」という結果でした。
これは、[帰無仮説]が正しいと仮定した時に今回のようなデータが得ら
れる確率 が[8.3]%であることを意味しています。
○ p値は有意水準よりも[ ]ので、[ ]を採択します。
つまり、有意な差は[ ]という結果になりました。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-50-320.jpg)
![【B】「夏期講習の前後で実力テストの点数の平均値に差があるか」を明らか
に するための推測統計の手順です。空欄を埋めましょう。
○ 推測統計を行った結果、「p=.083」という結果でした。
これは、[帰無仮説]が正しいと仮定した時に今回のようなデータが得ら
れる確率 が[8.3]%であることを意味しています。
○ p値は有意水準よりも[大きい]ので、[帰無仮説]を採択します。
つまり、有意な差は[ない]という結果になりました。
復習問題①](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-51-320.jpg)




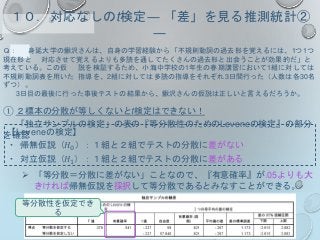
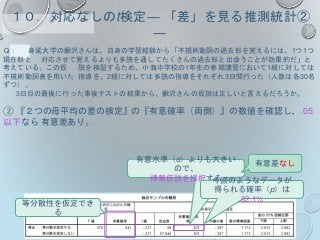


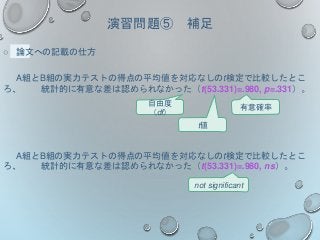
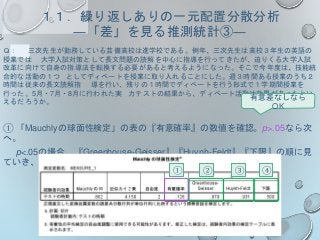








![【A】「小学3年生・小学5年生・中学1年生の語彙サイズに差があるか」を
明らかに するための推測統計の手順です。空欄を埋めましょう。
○ 帰無仮説、対立仮説はそれぞれ
帰無仮説[𝐻0]:3つの学年の語彙サイズには[ ]。
対立仮説[𝐻1]:3つの学年の語彙サイズには
[ ]。
○ 独立変数は[ ]つあり、[ ]です([ ]水準)。
従属変数は[ ]つあり、[ ]です。
別の人のデータを比較しているので、繰り返し[ ]の分析になりま
す。
したがって、[ ]という分析
方法を用います。
復習問題②](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-79-320.jpg)
![【A】「小学3年生・小学5年生・中学1年生の語彙サイズに差があるか」を
明らかに するための推測統計の手順です。空欄を埋めましょう。
○ 帰無仮説、対立仮説はそれぞれ
帰無仮説[𝐻0]:3つの学年の語彙サイズには[差がない]。
対立仮説[𝐻1]:3つの学年の語彙サイズには[どこかに差がある]。
○ 独立変数は[ ]つあり、[ ]です([ ]水準)。
従属変数は[ ]つあり、[ ]です。
別の人のデータを比較しているので、繰り返し[ ]の分析になりま
す。
したがって、[ ]という分析
方法を用います。
復習問題②](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-80-320.jpg)
![【A】「小学3年生・小学5年生・中学1年生の語彙サイズに差があるか」を
明らかに するための推測統計の手順です。空欄を埋めましょう。
○ 帰無仮説、対立仮説はそれぞれ
帰無仮説[𝐻0]:3つの学年の語彙サイズには[差がない]。
対立仮説[𝐻1]:3つの学年の語彙サイズには[どこかに差がある]。
○ 独立変数は[1]つあり、[学年]です([3]水準)。
従属変数は[1]つあり、[語彙サイズ]です。
別の人のデータを比較しているので、繰り返し[なし]の分析になりま
す。
したがって、[繰り返しなしの一元配置分散分析]という分析方法を用い
ます。
復習問題②](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-81-320.jpg)
![【A】「小学3年生・小学5年生・中学1年生の語彙サイズに差があるか」を
明らかに するための推測統計の手順です。空欄を埋めましょう。
○ 分析を行う前に[ ]が仮定できるかどうかを確認します。
[ ]の検定において有意確率が.05よりも[ ]ければ、
分散分析を行ってよいです。
○ 推測統計を行った結果、「p=.003」という結果でした。
これは、[ ]が正しいと仮定した時に今回のようなデータが
得られる確率 が[ ]%であることを意味しています。
p値は有意水準よりも[ ]ので、[ ]を採択します。
つまり、[ ] があるという結果になりました。
復習問題②](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-82-320.jpg)
![【A】「小学3年生・小学5年生・中学1年生の語彙サイズに差があるか」を
明らかに するための推測統計の手順です。空欄を埋めましょう。
○ 分析を行う前に[等分散性]が仮定できるかどうかを確認します。
[等分散性]の検定において有意確率が.05よりも[大き]ければ、分散分
析を行っ てよいです。
○ 推測統計を行った結果、「p=.003」という結果でした。
これは、[ ]が正しいと仮定した時に今回のようなデータが
得られる確率 が[ ]%であることを意味しています。
p値は有意水準よりも[ ]ので、[ ]を採択します。
つまり、[ ] があるという結果になりました。
復習問題②](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-83-320.jpg)
![【A】「小学3年生・小学5年生・中学1年生の語彙サイズに差があるか」を
明らかに するための推測統計の手順です。空欄を埋めましょう。
○ 分析を行う前に[等分散性]が仮定できるかどうかを確認します。
[等分散性]の検定において有意確率が.05よりも[大き]ければ、分散分
析を行っ てよいです。
○ 推測統計を行った結果、「p=.003」という結果でした。
これは、[帰無仮説]が正しいと仮定した時に今回のようなデータが得ら
れる確率 が[0.3]%であることを意味しています。
p値は有意水準よりも[小さい]ので、[対立仮説]を採択します。つま
り、[主効果]があるという結果になりました。
復習問題②](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-84-320.jpg)







![復習問題③
① 健康診断シリーズ。身長は[ ]尺度、体重は[ ]尺度、座高
は[ ] 尺度。尿酸値(mg/dl)は[ ]尺度だが、「痛風かど
うか」は[ ]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-96-320.jpg)
![復習問題③
① 健康診断シリーズ。身長は[比例]尺度、体重は[比例]尺度、座高は
[比例] 尺度。尿酸値(mg/dl)は[比例]尺度だが、「痛風かどうか」は
[名義]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-97-320.jpg)
![復習問題③
② 学校シリーズ。出席番号は[ ]尺度、クラス名は[ ]尺度で
ある。また、 性別は[ ]尺度、学年は[ ]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-98-320.jpg)
![復習問題③
② 学校シリーズ。出席番号は[名義]尺度、クラス名は[名義]尺度で あ
る。また、 性別は[名義]尺度、学年は[順序]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-99-320.jpg)
![復習問題③
③ 所属する卒論ゼミによって卒論のページ数に差があるかを調べたい。卒論
の指 導教員は[ ]尺度、ページ数は[ ]尺度である。
なお、現在までに読んだ先行研究の数は[ ]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-100-320.jpg)
![復習問題③
③ 所属する卒論ゼミによって卒論のページ数に差があるかを調べたい。卒論
の指 導教員は[名義]尺度、ページ数は[比例]尺度である。
なお、現在までに読んだ先行研究の数は[比例]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-101-320.jpg)
![復習問題③
④ 所属する部活動と好きな飲み物の関係を調べたい。部活動は[ ]尺
度、好き な飲み物は[ ]尺度である。
ちなみにスポーツ飲料の売り上げランキングは[ ]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-102-320.jpg)
![復習問題③
④ 所属する部活動と好きな飲み物の関係を調べたい。部活動は[名義]尺
度、好き な飲み物は[名義]尺度である。
ちなみにスポーツ飲料の売り上げランキングは[順序]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-103-320.jpg)

![復習問題③
⑤ 利用年月日: 月/日はそれぞれ[ ]尺度。
午前・午後は[ ]尺度。
ご利用回数: (今回の測り方だと)[ ]尺度。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-105-320.jpg)
![復習問題③
⑤ 利用年月日: 月/日はそれぞれ[名義]尺度。
午前・午後は[名義]尺度。
ご利用回数: (今回の測り方だと)[順序]尺度。(名義尺度扱いの方
が無難かも)](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-106-320.jpg)
![復習問題③
⑥ ご性別: [ ]尺度。
ご年齢: (今回の測り方だと)[ ]尺度。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-107-320.jpg)
![復習問題③
⑥ ご性別: [名義]尺度。
ご年齢: (今回の測り方だと)[順序]尺度。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-108-320.jpg)
![復習問題③
⑦ 満足度: (今回の測り方だと) [ ]尺度。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-109-320.jpg)
![復習問題③
⑦ 満足度: (今回の測り方だと) [順序]尺度。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-110-320.jpg)
![復習問題③
⑧ 本日お召し上がりいただいた商品: [ ]尺度。
輝いていた従業員: [ ]尺度](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-111-320.jpg)
![復習問題③
⑧ 本日お召し上がりいただいた商品: [名義]尺度。
輝いていた従業員: [名義]尺度](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-112-320.jpg)
![復習問題③
⑨ また利用したいと思いますか:(今回の測り方だと) [ ]尺度。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-113-320.jpg)
![復習問題③
⑨ また利用したいと思いますか:(今回の測り方だと) [名義]尺度。
選択肢に順序性があると言えるか??](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-114-320.jpg)


















![復習問題④
① 統計(記述統計・推測統計)は、主として[ ]的アプロー
チの研究で 用いる。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-139-320.jpg)
![復習問題④
① 統計(記述統計・推測統計)は、主として[量]的アプロー
チの研究で 用いる。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-140-320.jpg)
![復習問題④
② データの分析方法は、データ収集の[ ]に考える。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-141-320.jpg)
![復習問題④
② データの分析方法は、データ収集の[前]に考える。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-142-320.jpg)
![復習問題④
③ 研究を通して明らかにしたい事象を持つ対象全体のことを[
]、 その研究で実際にデータを取る対象のことを[ ]
という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-143-320.jpg)
![復習問題④
③ 研究を通して明らかにしたい事象を持つ対象全体のことを
[母集 団]、 その研究で実際にデータを取る対象のことを[標
本]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-144-320.jpg)
![復習問題④
④ 母集団の様子を知るためには[ ]を、標本の様子を
記述 するためには[ ]を用いる。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-145-320.jpg)
![復習問題④
④ 母集団の様子を知るためには[推測統計]を、標本の様子を
記述 するためには[記述統計]を用いる。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-146-320.jpg)
![復習問題④
⑤ ある値(またはある範囲)に該当するデータの数を[ ]
といい、 [ ]や[ ]を用いて報告す
る。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-147-320.jpg)
![復習問題④
⑤ ある値(またはある範囲)に該当するデータの数を[度数]
といい、 [ヒストグラム]や[棒グラフ]を用いて報告す
る。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-148-320.jpg)
![復習問題④
⑥ ヒストグラムは[ ]尺度と[ ]尺度のデータ、
棒グラフは[ ]尺度と[ ]尺度のデータに対して用い
る。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-149-320.jpg)
![復習問題④
⑥ ヒストグラムは[間隔]尺度と[比例]尺度のデータ、
棒グラフは[名義]尺度と[順序]尺度のデータに対して用い
る。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-150-320.jpg)
![復習問題④
⑦ 平均値は[ ]尺度以上、中央値は[ ]尺度以上の
データで 計算してよい。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-151-320.jpg)
![復習問題④
⑦ 平均値は[間隔]尺度以上、中央値は[順序]尺度以上の
データで 計算してよい。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-152-320.jpg)
![復習問題④
⑧ 平均値は[ ]の影響を受けやすいので、中央値も合わ
せて 確認すべきである。
また間隔尺度以上のデータであれば、散布度として
[ ]も 合わせて報告する必要がある。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-153-320.jpg)
![復習問題④
⑧ 平均値は[外れ値]の影響を受けやすいので、中央値も合わ
せて 確認すべきである。
また間隔尺度以上のデータであれば、散布度として[標準偏
差]も 合わせて報告する必要がある。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-154-320.jpg)
![復習問題④
⑨ 尺度は、データがどのような性質を持っているかを表すもの
である。 [ ]尺度、 [ ]尺度、 [ ]尺度、
[ ]尺度の順に情報 量が多い。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-155-320.jpg)
![復習問題④
⑨ 尺度は、データがどのような性質を持っているかを表すもの
である。 [比例]尺度、 [間隔]尺度、 [順序]尺度、 [名
義]尺度の順に情報 量が多い。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-156-320.jpg)
![復習問題④
⑩ 左右対称で、中央に山が1つあり、両すそがなだらかに広
がった分 布のことを[ ]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-157-320.jpg)
![復習問題④
⑩ 左右対称で、中央に山が1つあり、両すそがなだらかに広
がった分 布のことを[正規分布]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-158-320.jpg)
![復習問題④
⑪ 平均値が0、標準偏差が1になるように変換した正規分布の
ことを [ ]という。また、この分布になる
ように変換した得点 のことを[ ]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-159-320.jpg)
![復習問題④
⑪ 平均値が0、標準偏差が1になるように変換した正規分布の
ことを [標準正規分布]という。また、この分布になるように
変換した得点 のことを[z得点]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-160-320.jpg)
![復習問題④
⑫ ピアソンの積率相関係数は2つの量的変数の
[ ]の強さ を数値で表すもので、[ ]≦r≦
[ ]の範囲の値を取る。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-161-320.jpg)
![復習問題④
⑫ ピアソンの積率相関係数は2つの量的変数の[直線的関係]
の強さ を数値で表すもので、[ -1 ]≦r≦[ 1 ]の範囲の値を
取る。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-162-320.jpg)
![復習問題④
⑬ 0<r≦1であれば[ ]の相関、-1≦r<0であれば[ ]の
相関が あるという。r=0のときは[ ]である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-163-320.jpg)
![復習問題④
⑬ 0<r≦1であれば[正]の相関、-1≦r<0であれば[負]の相
関が あるという。r=0のときは[無相関]である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-164-320.jpg)
![復習問題④
⑭ 相関係数(r)を二乗した𝑟2のことを[ ]とい
う。
𝑟2は、変量Aの変動の何%を変量Bの変動で説明できるかを表
す。
rは[ ]尺度、𝑟2
は[ ]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-165-320.jpg)
![復習問題④
⑭ 相関係数(r)を二乗した𝑟2のことを[決定係数]という。
𝑟2
は、変量Aの変動の何%を変量Bの変動で説明できるかを表
す。
rは[順序]尺度、𝑟2
は[比例]尺度である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-166-320.jpg)
と
[ ](𝐻1)を立てる。
𝐻0は差・関係が[ ]という仮説、 𝐻1は差・関係が
[ ]という 仮説である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-167-320.jpg)
と[対立仮説]
(𝐻1)を立てる。
𝐻0は差・関係が[ない]という仮説、 𝐻1は差・関係が[あ
る]という 仮説である。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-168-320.jpg)
![復習問題④
⑯ 帰無仮説が正しいと仮定した場合に標本のようなデータが得
られる 確率を[ ( )]という。
この確率が[ ( )]よりも小さければ、帰無
仮説を[ ] して対立仮説を[ ]する。つまり、差や
関係が[ ]という結果 になる。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-169-320.jpg)
![復習問題④
⑯ 帰無仮説が正しいと仮定した場合に標本のようなデータが得
られる 確率を[有意確率(p)]という。
この確率が[有意水準(α)]よりも小さければ、帰無仮説を
[棄却] して対立仮説を[採択]する。つまり、差や関係が
[ある]という結果 になる。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-170-320.jpg)
![復習問題④
⑰ 本当は差がないのに差があるという結果を出してしまうこと
を [ ]、本当は差があるのに差がないという結果
を出して しまうことを[ ]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-171-320.jpg)
![復習問題④
⑰ 本当は差がないのに差があるという結果を出してしまうこと
を [第1種の誤り]、本当は差があるのに差がないという結果
を出して しまうことを[第2種の誤り]という。](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-172-320.jpg)



![復習問題④
⑲ 何尺度でしょう。
性別 :[ ]尺度
年齢 :[ ]尺度(今回の場合)
ご職業 :[ ]尺度](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-176-320.jpg)
![復習問題④
⑲ 何尺度でしょう。
性別 :[名義]尺度
年齢 :[順序]尺度(今回の場合)
ご職業 :[名義]尺度](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-177-320.jpg)
![復習問題④
⑳ 何尺度でしょう。
ご利用されたきっかけは? :[ ]尺度
何名様で? :[ ]尺度(今回の場合)](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-178-320.jpg)
![復習問題④
⑳ 何尺度でしょう。
ご利用されたきっかけは? :[名義]尺度
何名様で? :[順序]尺度(今回の場合)](https://image.slidesharecdn.com/201708-170821172804/85/2017-08-24-179-320.jpg)