Downloaded 175 times
![Hydraulic Conductivity
• Has dimensions of velocity [L/T]
• A combined property of the medium and the fluid
• Ease with which fluid moves through the medium
k = cd2 intrinsic permeability
ρ = density
µ = dynamic viscosity
g = specific weight
Porous medium property
Fluid properties](https://image.slidesharecdn.com/03-darcyslaw-150610082744-lva1-app6891/85/03-darcys-law-12-320.jpg)
Uploaded byUsama Waly
03 darcys law
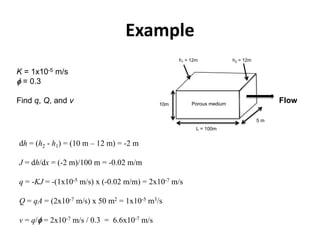
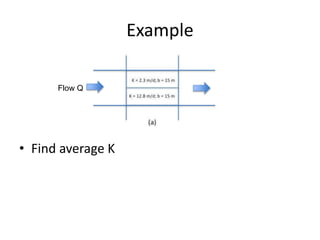
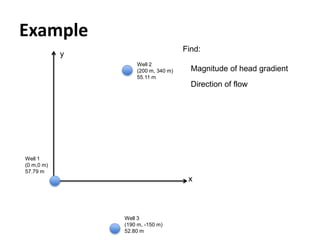
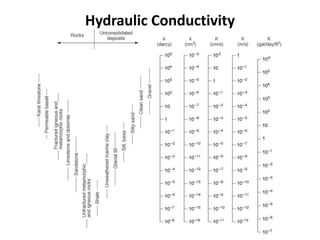
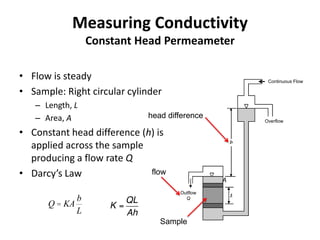
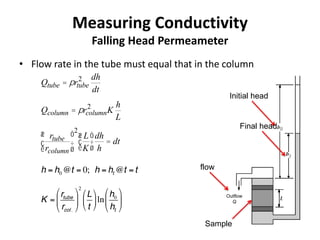
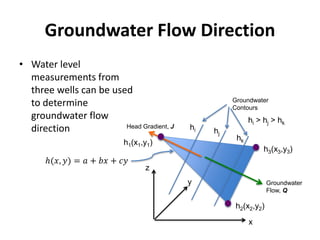
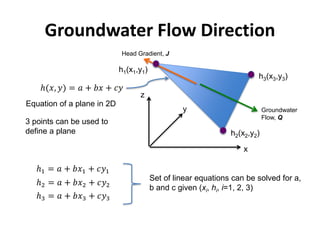
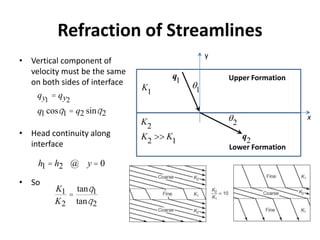
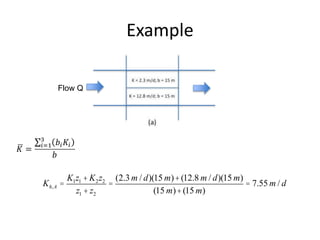
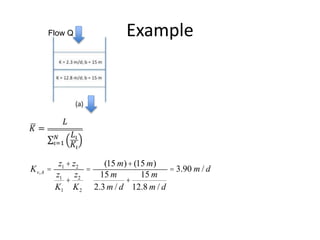
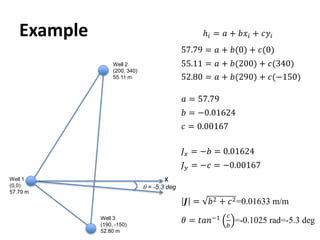
- Darcy's law relates the specific discharge of groundwater to the hydraulic gradient and hydraulic conductivity. It was established based on experiments by Henry Darcy. - Hydraulic conductivity is a property of both the porous medium and fluid that describes the ease of groundwater flow. It can be estimated using the Kozeny-Carman equation or measured in the lab using permeameters. - Groundwater flow is heterogeneous and anisotropic in layered or stratified aquifers. The generalized form of Darcy's law accounts for variable conductivity in different directions. Streamlines refract at interfaces between layers with different conductivities.
More Related Content
![Geotechnical Engineering-I [Lec #23: Soil Permeability]](https://cdn.slidesharecdn.com/ss_thumbnails/23-180924141141-thumbnail.jpg?width=640&height=640&fit=bounds)
03 darcys law
- 1. Darcy’s law Groundwater Hydraulics DaeneC. McKinney
- 2. Outline • Properties –Aquifer Storage • Darcy’s Law • Hydraulic Conductivity • Heterogeneity and Anisotropy • Refraction of Streamlines • Generalized Darcy’s Law
- 3. Aquifer Storage • Storativity(S) - ability of an aquifer to store water • Change in volume of stored water due to change in piezometric head. • Volume of water released (taken up) from aquifer per unit decline (rise) in piezometric head. Unit area Unit decline in head Released water
- 4. Aquifer Storage • FluidCompressibility (b) • Aquifer Compressibility (a) • Confined Aquifer – Water produced by 2 mechanisms 1. Aquifer compaction due to increasing effective stress 2. Water expansion due to decreasing pressure • Unconfined aquifer – Water produced by draining pores gV a S = rg(a +fb) S = Sy
- 5. Unconfined Aquifer Storage •Storativity of an unconfined aquifer (Sy, specific yield) depends on pore space drainage. • Some water will remain in the pores - specific retention, Sr • Sy = f – Sr Unit area Unit decline in head Released water
- 6. Porosity, Specific Yield,& Specific Retention yr SS f
- 7. Confined Aquifer Storage •Storativity of a confined aquifer (Ss) depends on both the compressibility of the water (b) and the compressibility of the porous medium itself (a). Unit area Unit decline in head Released water
- 8. Example • Storage ina sandstone aqufier • f = 0.1, a = 4x10-7 ft2/lb, b = 2.8x10-8 ft2/lb, g = 62.4 lb/ft3 • ga 2.5x10-5 ft-1 and gbf 1.4x10-7 ft-1 • Solid Fluid • 2 orders of magnitude more storage in solid • b = 100 ft, A = 10 mi2 = 279,000,000 ft2 S = Ss*b = 2.51x10-3 • If head in the aquifer is lowered 3 ft, what volume is released? V = SAh = 2.1x10-6 ft3
- 9.
- 10. hL z1 z2 P1/g P2/g Q Q L v Sand column Datum plane Area,A h1 h2 Darcy’s Experiments •Discharge is Proportional to – Area – Head difference Inversely proportional to – Length • Coefficient of proportionality is K = hydraulic conductivity L hh AQ 21 Q = -KA h2 -h1 L Q = -KA Dh L
- 11. Darcy’s Data 0 5 10 15 20 25 30 35 0 510 15 20 Flow,Q(l/min) Gradient (m/m) Set 1, Series 1 Set 1, Series 2 Set 1, Series 3 Set 1, Series 4 Set 2
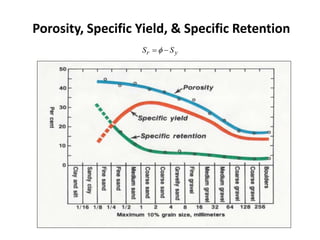
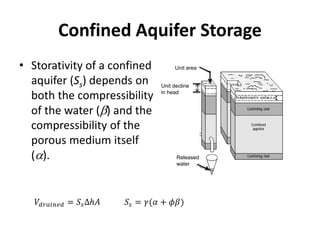
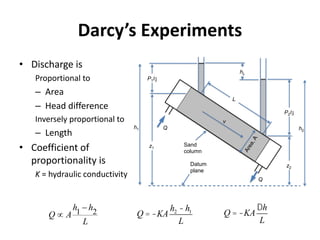
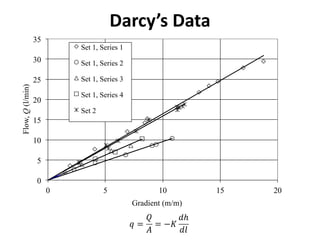
- 12. Hydraulic Conductivity • Hasdimensions of velocity [L/T] • A combined property of the medium and the fluid • Ease with which fluid moves through the medium k = cd2 intrinsic permeability ρ = density µ = dynamic viscosity g = specific weight Porous medium property Fluid properties
- 13.
- 14. Groundwater Velocity • q- Specific discharge Discharge from a unit cross- section area of aquifer formation normal to the direction of flow. • v - Average velocity Average velocity of fluid flowing per unit cross- sectional area where flow is ONLY in pores. A Q q ff A Qq v
- 15. dh = (h2- h1) = (10 m – 12 m) = -2 m J = dh/dx = (-2 m)/100 m = -0.02 m/m q = -KJ = -(1x10-5 m/s) x (-0.02 m/m) = 2x10-7 m/s Q = qA = (2x10-7 m/s) x 50 m2 = 1x10-5 m3/s v = q/f = 2x10-7 m/s / 0.3 = 6.6x10-7 m/s /” h1 = 12m h2 = 12m L = 100m 10m 5 m FlowPorous medium Example K = 1x10-5 m/s f = 0.3 Find q, Q, and v
- 16. Hydraulic Gradient Gradient vectorpoints in the direction of greatest rate of increase of h Specific discharge vector points in the opposite direction of h
- 17. Well Pumping inan Aquifer Aquifer (plan view) y h1 < h2 < h3 x h1 h2 h3 Well, Q q h Circular hydraulic head contours K, conductivity, Is constant Hydraulic gradient Specific discharge
- 18. Validity of Darcy’sLaw • We ignored kinetic energy (low velocity) • We assumed laminar flow • We can calculate a Reynolds Number for the flow q = Specific discharge d10 = effective grain size diameter • Darcy’s Law is valid for NR < 1 (maybe up to 10) NR = rqd10 m
- 19. Specific Discharge vsHead Gradient q Re = 10 Re = 1 Experiment shows this a tan-1(a)= (1/K) Darcy Law predicts this
- 20. Estimating Conductivity Kozeny –Carman Equation • Kozeny used bundle of capillary tubes model to derive an expression for permeability in terms of a constant (c) and the grain size (d) • So how do we get the parameters we need for this equation? 2 2 3 2 )1(180 dcdk f f Kozeny – Carman eq.
- 21. Measuring Conductivity Permeameter LabMeasurements • Darcy’s Law is useless unless we can measure the parameters • Set up a flow pattern such that – We can derive a solution – We can produce the flow pattern experimentally • Hydraulic Conductivity is measured in the lab with a permeameter – Steady or unsteady 1-D flow – Small cylindrical sample of medium
- 22. Measuring Conductivity Constant HeadPermeameter • Flow is steady • Sample: Right circular cylinder – Length, L – Area, A • Constant head difference (h) is applied across the sample producing a flow rate Q • Darcy’s Law Continuous Flow Outflow Q Overflow A Q = KA b L Sample head difference flow
- 23. Measuring Conductivity Falling HeadPermeameter • Flow rate in the tube must equal that in the column Outflow Q Qcolumn = prcolumn 2 K h L Qtube = prtube 2 dh dt rtube rcolumn æ è ç ö ø ÷ 2 L K æ è ç ö ø ÷ dh h = dt Sample flow Initial head Final head
- 24. Heterogeneity and Anisotropy •Homogeneous – Properties same at every point • Heterogeneous – Properties different at every point • Isotropic – Properties same in every direction • Anisotropic – Properties different in different directions • Often results from stratification during sedimentation verticalhorizontal KK www.usgs.gov
- 25. Example • a =???, b = 4.673x10-10 m2/N, g = 9798 N/m3, • S = 6.8x10-4, b = 50 m, f = 0.25, • Saquifer = gabb ??? • Swater = gbfb • % storage attributable to water expansion • • %storage attributable to aquifer expansion •
- 26. Layered Porous Media (FlowParallel to Layers) 3K 2K 1K W b 1b 2b 3b 1Q 2Q 3Q h h2 h1 Piezometric surface Q datum
- 27. Layered Porous Media (FlowPerpendicular to Layers) Q 3K2K1K b Q L L3L2L1 h1 Piezometric surface h2 h3 h
- 28. Example • Find averageK Flow Q
- 29. Example • Find averageK Flow Q
- 30. Anisotrpoic Porous Media •General relationship between specific discharge and hydraulic gradient K is symmetric, i.e., Kij = Kji.
- 31. Principal Directions • Oftenwe can align the coordinate axes in the principal directions of layering • Horizontal conductivity often order of magnitude larger than vertical conductivity qx = -Kxx ¶h ¶x qy = -Kyy ¶h ¶y qz = -Kzz ¶h ¶z qx qy qz é ë ê ê ê ù û ú ú ú = - Kxx 0 0 0 Kyy 0 0 0 Kzz é ë ê ê ê ù û ú ú ú ¶h ¶x ¶h ¶y ¶h ¶z é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú Kxx = Kyy = KHoriz >> Kzz = KVert
- 32. Groundwater Flow Direction •Water level measurements from three wells can be used to determine groundwater flow direction Groundwater Contours Groundwater Flow, Q x y z Head Gradient, J hk hj hi hi > hj > hk h1(x1,y1) h3(x3,y3) h2(x2,y2)
- 33. Groundwater Flow Direction Magnitudeof head gradient = Angle of head gradient = Head gradient =
- 34. Groundwater Flow Direction Setof linear equations can be solved for a, b and c given (xi, hi, i=1, 2, 3) 3 points can be used to define a plane Equation of a plane in 2D Groundwater Flow, Q x y z Head Gradient, J h1(x1,y1) h3(x3,y3) h2(x2,y2)
- 35. Groundwater Flow Direction Negativeof head gradient in x direction Negative of head gradient in y direction Magnitude of head gradient Direction of flow
- 36. x Well 2 (200 m,340 m) 55.11 m Well 1 (0 m,0 m) 57.79 m Well 3 (190 m, -150 m) 52.80 m Example Find: Magnitude of head gradient Direction of flow y
- 37. Contour Map ofGroundwater Levels • Contours of groundwater level (equipotential lines) and Flowlines (perpendicular to equipotiential lines) indicate areas of recharge and discharge
- 38. Refraction of Streamlines •Vertical component of velocity must be the same on both sides of interface • Head continuity along interface • So 2K 1K Upper Formation 12 KK y x 1 2 2q 1q Lower Formation qy1 = qy2 q1 cosq1 = q2 sinq2 h1 = h2 @ y = 0 K1 K2 = tanq1 tanq2
- 39. Summary • Properties –Aquifer Storage • Darcy’s Law – Darcy’s Experiment – Specific Discharge – Average Velocity – Validity of Darcy’s Law • Hydraulic Conductivity – Permeability – Kozeny-Carman Equation – Constant Head Permeameter – Falling Head Permeameter • Heterogeneity and Anisotropy – Layered Porous Media • Refraction of Streamlines • Generalized Darcy’s Law
- 40.
- 41. Example • a =???, b = 4.673x10-10 m2/N, g = 9798 N/m3, • S = 6.8x10-4, b = 50 m, f = 0.25, • Saquifer = gabb ??? • Swater = gbfb = (9798 N/m3)(4.673x10-10 m2/N)(0.25)(50 m) • = 5.72x10-5 • percent of storage coefficient attributable to water expansion • = Swater /S = 5.72x10-5 /6.8x10-4 *100 = 8.4% • percent of storage coefficient attributable to aquifer expansion • = Saquifer /S = 1 – (Swater /S ) = 91.6%
- 42. Example Flow Q Kh,A = K1z1+ K2z2 z1 + z2 = (2.3 m / d)(15 m)+(12.8 m / d)(15 m) (15 m)+(15 m) = 7.55 m / d
- 43. ExampleFlow Q Kv,A = z1+ z2 z1 K1 + z2 K2 = (15 m)+(15 m) 15 m 2.3 m / d + 15 m 12.8 m / d = 3.90 m / d
- 44. x = -5.3deg Well 2 (200, 340) 55.11 m Well 1 (0,0) 57.79 m Well 3 (190, -150) 52.80 m Example