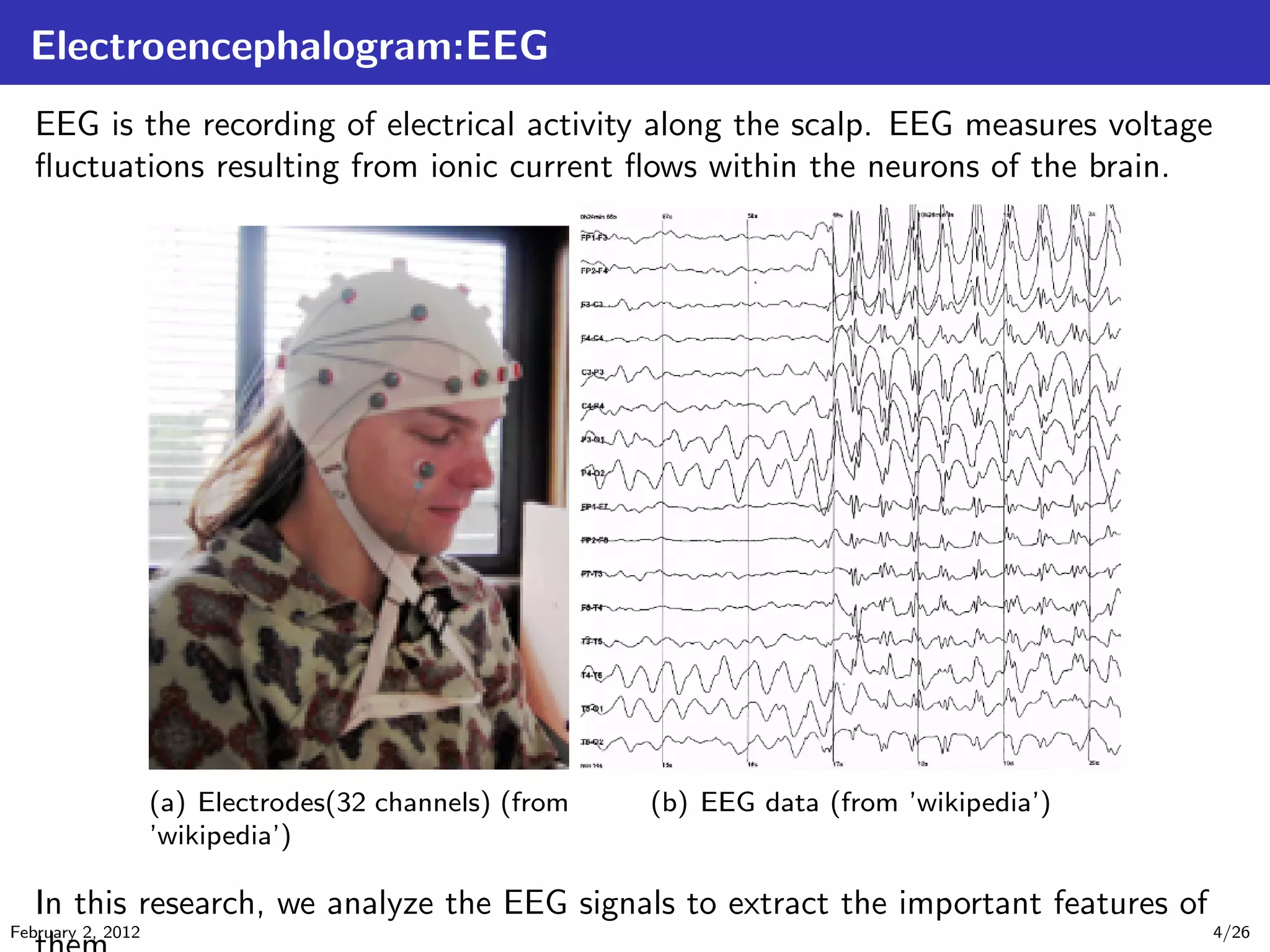
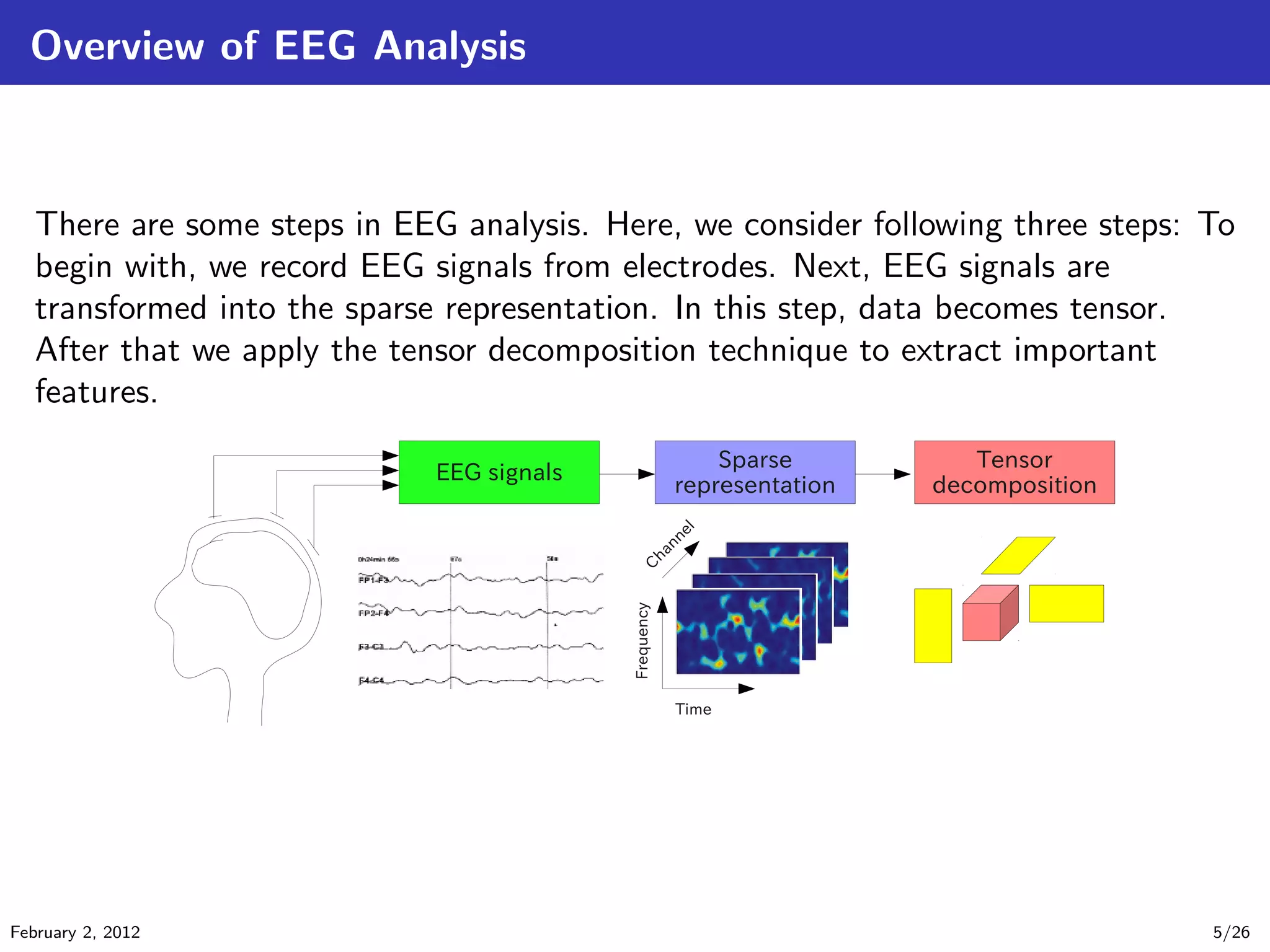
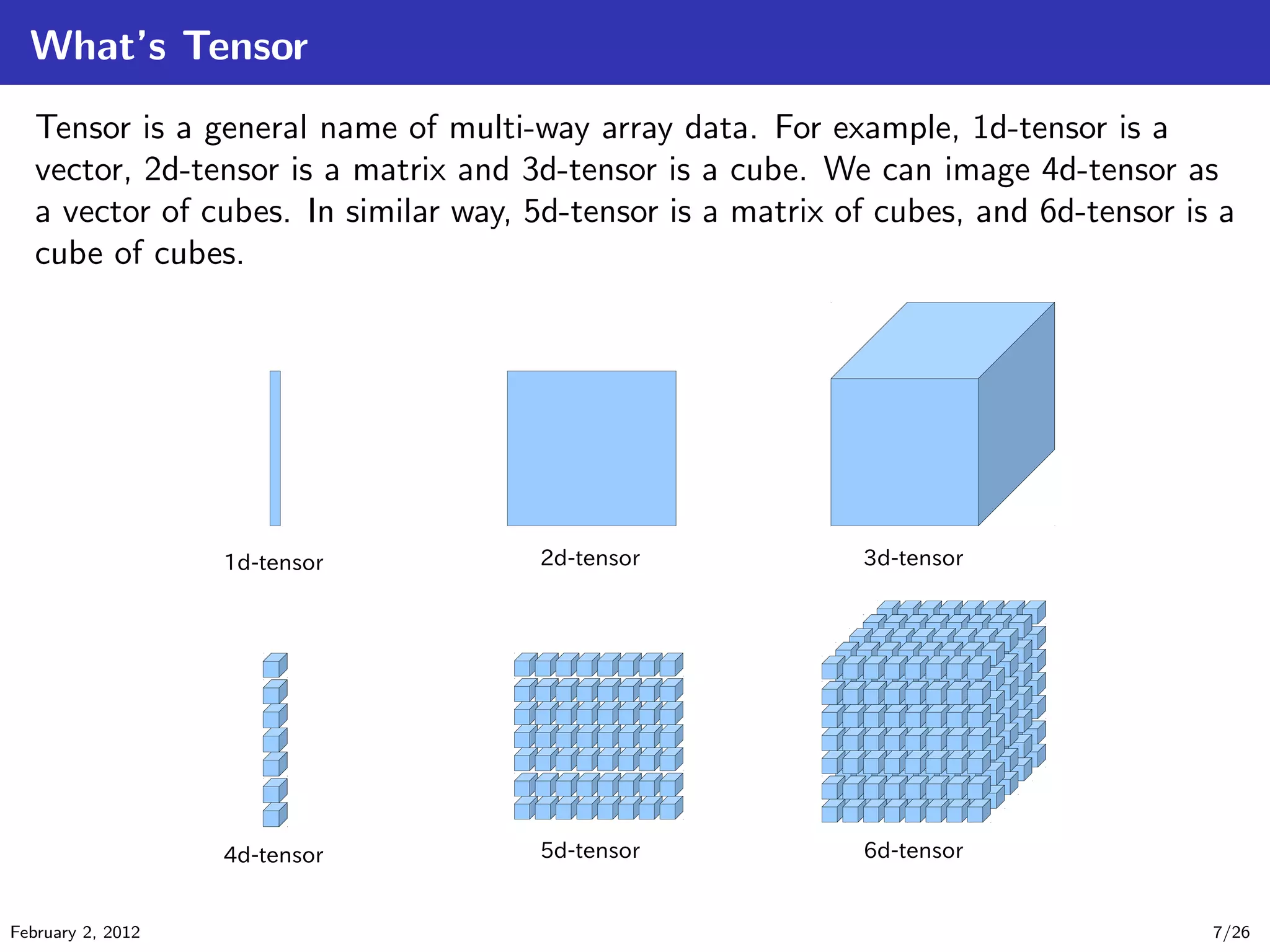
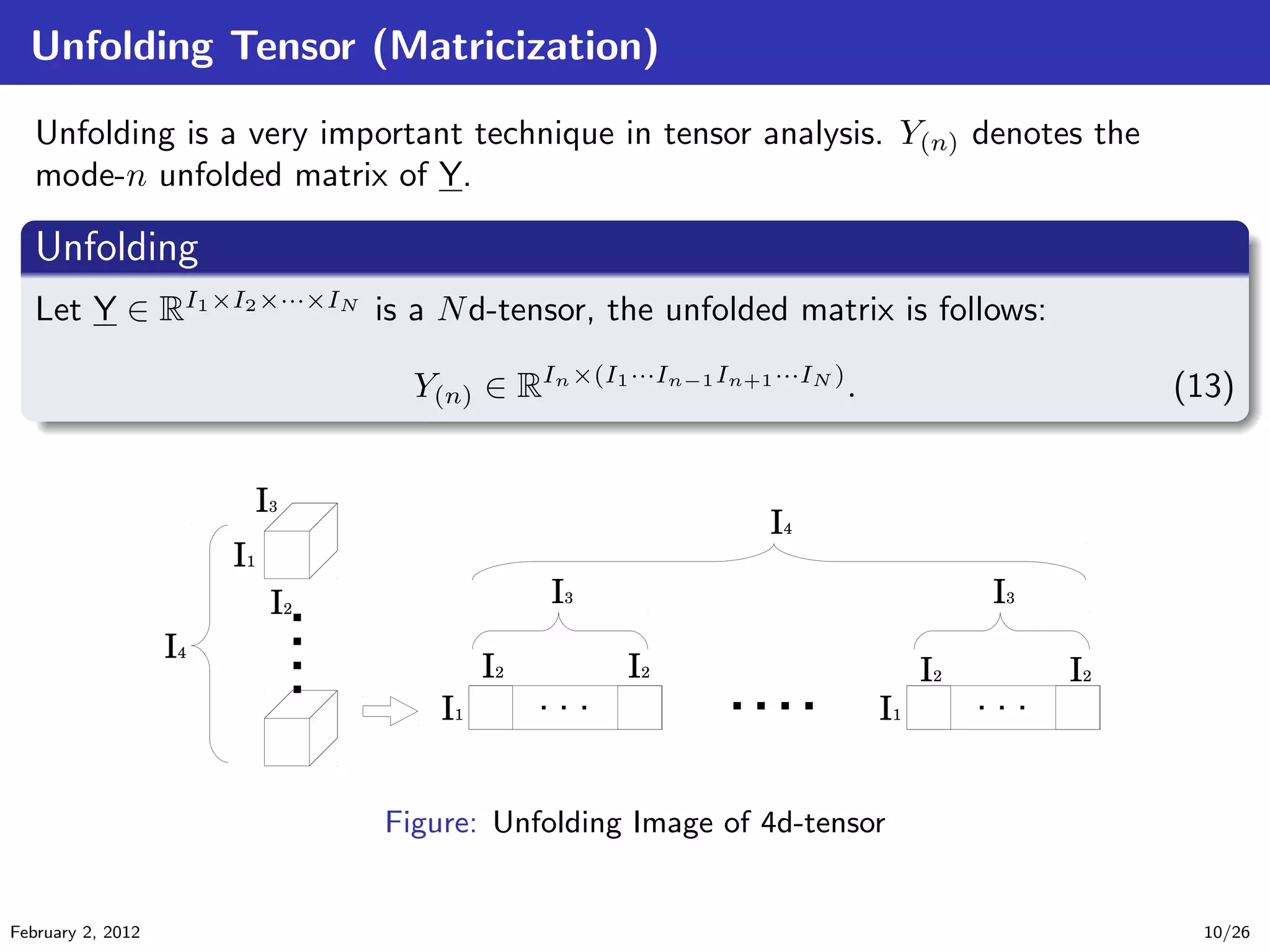
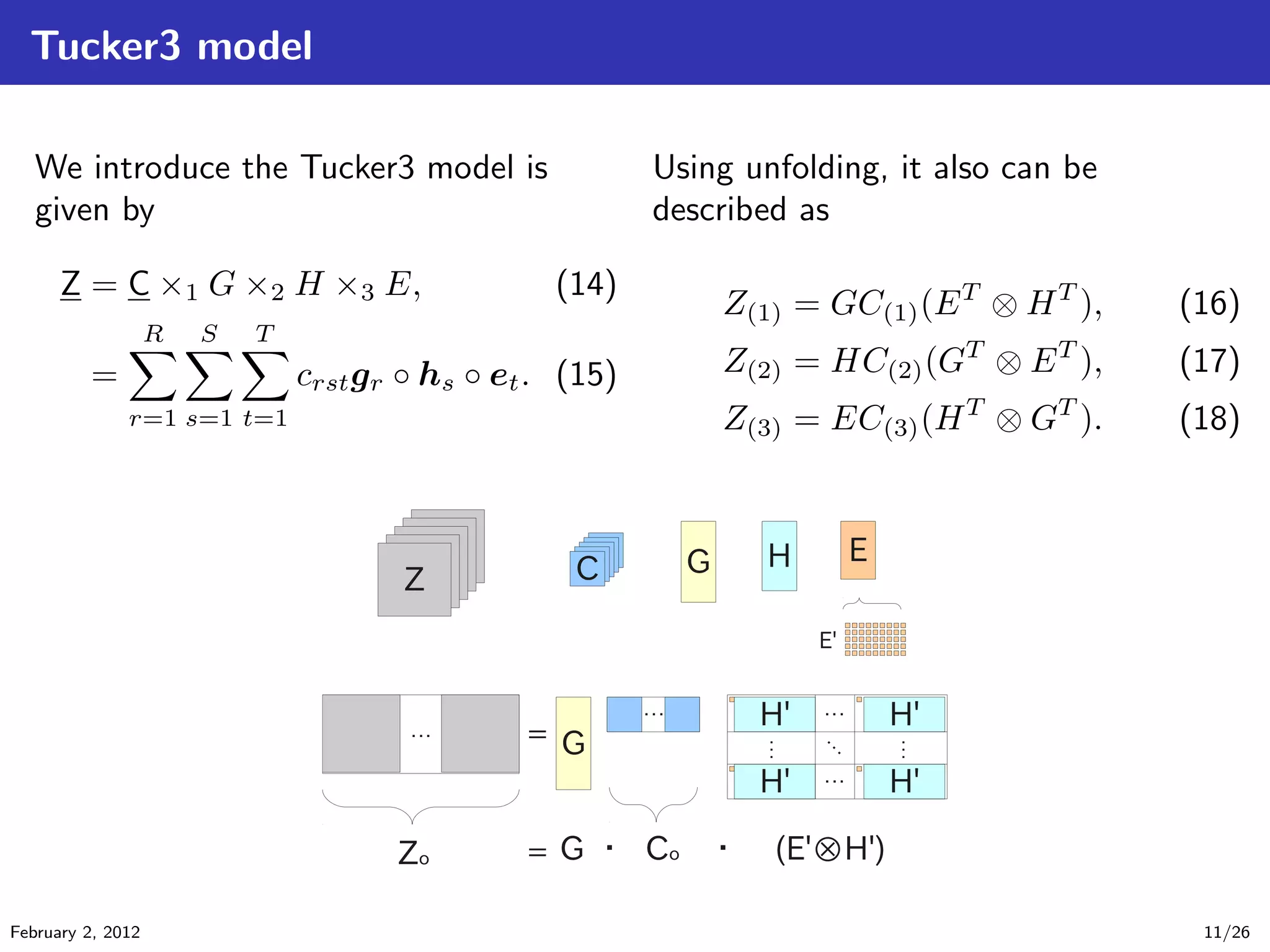
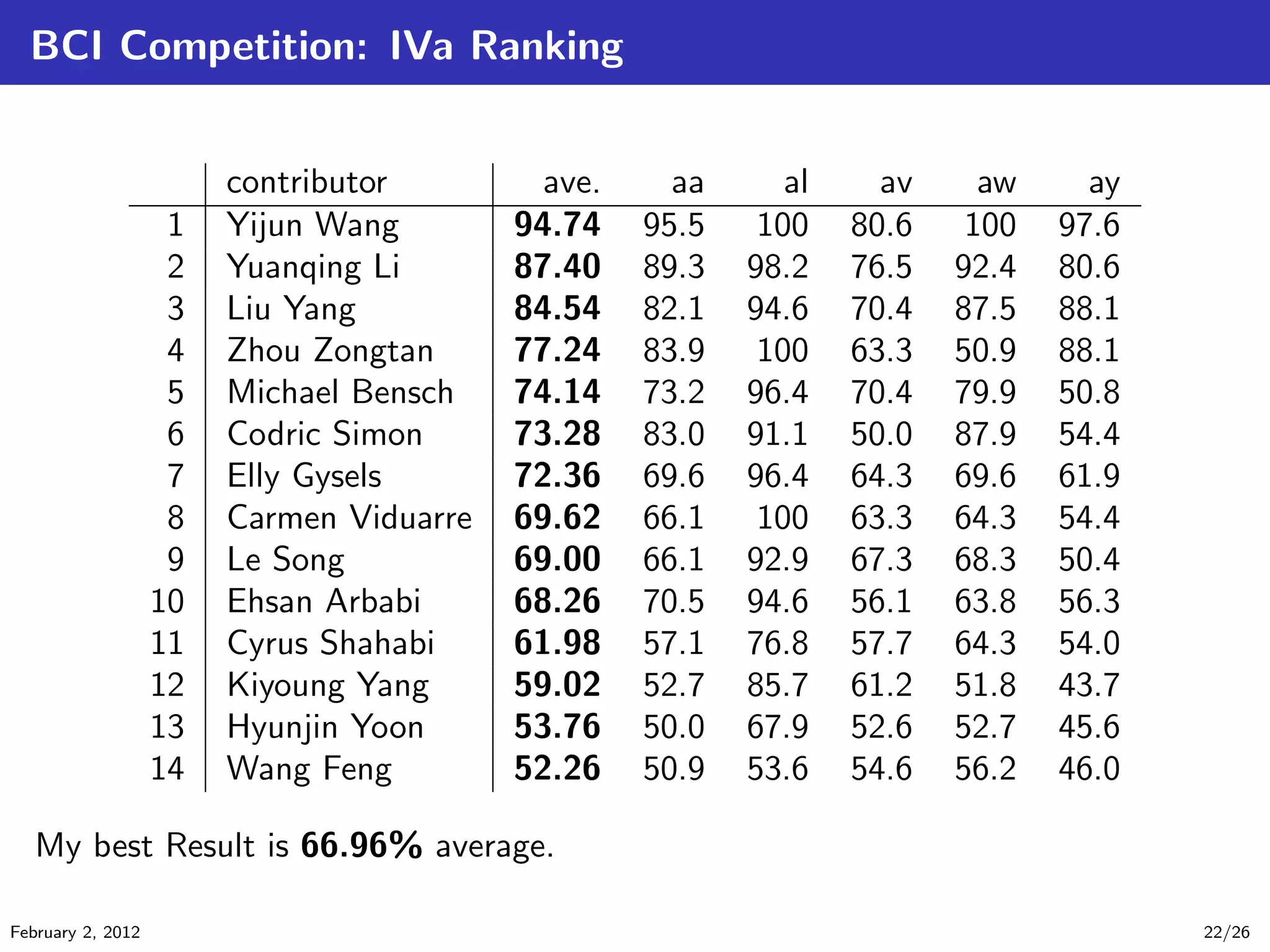
The document details tensor analysis techniques for EEG data in the context of brain-computer interfaces (BCIs), emphasizing the importance of non-invasive methods like EEG due to their low cost and risk. It outlines steps in EEG analysis, introduces tensor calculations and decompositions, and presents experimental results comparing different classification methods. The findings are based on data obtained from a BCI competition involving motor imagery classification.

1. .
.
. ..
.
.
Tensor Analysis for EEG data
Tatsuya Yokota
Tokyo Institute of Technology
February 2, 2012
February 2, 2012 1/26

2. Outline
.
..1 Introduction
.
..2 Principal Component Analysis
.
..3 Experiments
.
..4 Summary
February 2, 2012 2/26

3. Brain Computer Interface
A brain-computer interface(BCI) is a direct communication pathway between the
brain and an external device. BCIs are often aimed at assisting, augmenting, or
repairing human cognitive or sensory-motor functions. BCIs can be separated into
three approaches as follow:
Invasive BCIs
Partially-invasive BCIs (ECoG)
Non-invasive BCIs (EEG, MEG, MRI, fMRI)
Invasive and partially-invasive BCIs are accurate. However there are risks of the
infection and the damage. Furthermore, it requires the operation to set the
electrodes in the head.
On the other hand, non-invasive BCIs are inferior than invasive BCIs in accuracy,
but costs and risks are very low. Especially, EEG approach is the most studied
potential non-invasive interface, mainly due to its fine temporal resolution, ease of
use, portability and low set-up cost.
February 2, 2012 3/26

4. Electroencephalogram:EEG
EEG is the recording of electrical activity along the scalp. EEG measures voltage
fluctuations resulting from ionic current flows within the neurons of the brain.
(a) Electrodes(32 channels) (from
’wikipedia’)
(b) EEG data (from ’wikipedia’)
In this research, we analyze the EEG signals to extract the important features of
February 2, 2012 4/26

5. Overview of EEG Analysis
There are some steps in EEG analysis. Here, we consider following three steps: To
begin with, we record EEG signals from electrodes. Next, EEG signals are
transformed into the sparse representation. In this step, data becomes tensor.
After that we apply the tensor decomposition technique to extract important
features.
February 2, 2012 5/26

6. Wavelet Transform for Sparse Representation
[Goupillaud et al., 1984]
In the first, we introduce the wavelet transform (WT) as one of the approaches for
sparse representation. The wavelet transform is given by
W(b, a) =
1
√
a
∞
−∞
f(t)ψ
t − b
a
dt, (1)
where f(t) is a signal, ψ(t) is a wavelet function. There are many kind of wavelets
such as Haar wavelet, Meyer wavelet, Mexican Hat wavelet and Morlet wavelet. In
this research, we use the Complex MORlet wavelet (CMOR) which is given by
ψfb,fc (t) =
1
√
πfb
ei2πfct−(t2
/fb)
. (2)
February 2, 2012 6/26

7. What’s Tensor
Tensor is a general name of multi-way array data. For example, 1d-tensor is a
vector, 2d-tensor is a matrix and 3d-tensor is a cube. We can image 4d-tensor as
a vector of cubes. In similar way, 5d-tensor is a matrix of cubes, and 6d-tensor is a
cube of cubes.
February 2, 2012 7/26

8. Tensor Calculation
We introduce some important calculations for tensor algebra. A tensor is
described as
Y ∈ RI1×I2×···×IN
. (3)
And each element of Y is described as yi1,i2,...,iN
.
.
mode-n tensor matrix product
..
.
. ..
.
.
Y = G ×n A, (4)
yi1,...,j,...,iN
=
In
in=1
gi1,...,in,...,iN
ain,j, (5)
where Y ∈ RI1×···×J×···×IN
, G ∈ RI1×···×IN
, and A ∈ RIn×J
.
We have following calculation rules:
(G ×n A) ×m B = (G ×m B) ×n A = G ×n A ×m B, (6)
(G ×n A) ×n B = G ×n (BA). (7)
February 2, 2012 8/26

9. Outer product and Kronecker product
The outer product of vectors is given by
A = a ◦ b = abT
∈ RI×J
, (8)
Z = a ◦ b ◦ c ∈ RI×J×K
, (9)
Y = a(1)
◦ · · · ◦ a(N)
∈ RI1×···×IN
. (10)
The Kronecker product of two matrices A ∈ RI×J
and B ∈ RT ×R
is a matrix
denoted as
A ⊗ B ∈ RIT ×JR
(11)
and defined as
A ⊗ B =





a11B a12B · · · a1J B
a21B a22B · · · a2J B
...
...
...
...
aI1B aI2B · · · aIJ B





. (12)
February 2, 2012 9/26

10. Unfolding Tensor (Matricization)
Unfolding is a very important technique in tensor analysis. Y(n) denotes the
mode-n unfolded matrix of Y.
.
Unfolding
..
.
. ..
.
.
Let Y ∈ RI1×I2×···×IN
is a Nd-tensor, the unfolded matrix is follows:
Y(n) ∈ RIn×(I1···In−1In+1···IN )
. (13)
Figure: Unfolding Image of 4d-tensor
February 2, 2012 10/26

11. Tucker3 model
We introduce the Tucker3 model is
given by
Z = C ×1 G ×2 H ×3 E, (14)
=
R
r=1
S
s=1
T
t=1
crstgr ◦ hs ◦ et. (15)
Using unfolding, it also can be
described as
Z(1) = GC(1)(ET
⊗ HT
), (16)
Z(2) = HC(2)(GT
⊗ ET
), (17)
Z(3) = EC(3)(HT
⊗ GT
). (18)
February 2, 2012 11/26

12. Tucker Decomposition (general formula)
Tucher Model is a very famous and general model of tensor decomposition. Given
tensor Y is decomposed into a set of matrices {A(n)
}N
n=1 and one small core
tensor G.
.
Tucker Model
..
.
. ..
.
.
Y = G ×1 A(1)
×2 A(2)
· · · ×N A(N)
(19)
=
J1
j1=1
· · ·
JN
jN =1
gj1,...,jN a
(1)
j1
◦ · · · ◦ a
(N)
jN
(20)
Furthermore, it can be described as follow by using unfolding.
.
Unfolded Tucker Model
..
.
. ..
.
.
Y(n) = A(n)
G(n)(A(N)
⊗ · · · ⊗ A(n+1)
⊗ A(n−1)
⊗ · · · ⊗ A(1)
)T
(21)
February 2, 2012 12/26

13. Kind of Tensor Decomposition [Cichocki et al., 2009]
The degree of freedom of tensor decomposition is very large. So there are many
methods of tensor decomposition. The kind of tensor decomposition is depend on
the constraint. For example, if we constrain the matrices {A(n)
}N
n=1 and the core
tensor G as non-negative matrices and tensor, then this method is the
non-negative tensor factorization (NTF). And if we consider the in-dependency
constraint, then this method is the independent component analysis (ICA). And if
we consider the sparsity constraints, then it is the sparse component analysis
(SCA). And if we consider the orthogonal constraints, then it is the principal
component analysis (PCA).
February 2, 2012 13/26

14. Principal Component Analysis
[Kroonenberg and de Leeuw, 1980] [Henrion, 1994]
Principal Component Analysis (PCA) is very typical method for signal analysis. In
this slide, we explain PCA in case of 3d-tensor decomposition. The tensor
decomposition model is given by
Z = C ×1 G ×2 H ×3 E. (22)
And the criterion of PCA is given by
.
Criterion for PCA
..
.
. ..
.
.
minimize ||Z − C ×1 G ×2 H ×3 E||2
F (23)
subject to GT
G = I, HT
H = I, ET
E = I. (24)
The goal of this criterion is to minimize the error of decomposed model, subject
to the matrices {G, H, E} are orthogonal. And (23) also can be described as
follow by using unfolding:
min ||Z(1) − GC(1)(E ⊗ H)T
||2
F . (25)
February 2, 2012 14/26

15. Criterion for 3-way PCA
Criterion for 3-way PCA is given by
minimize f := ||Z(1) − GC(1)(ET
⊗ HT
)||2
F (26)
subject to GT
G = I, ET
E = I, HT
H = I. (27)
From (27),
C(1) = GT
Z(1)(E ⊗ H). (28)
Substituting (28) into f,
f = ||Z(1) − GGT
Z(1)(E ⊗ H)(ET
⊗ HT
)||2
F (29)
= tr(Z(1)ZT
(1)) − tr(GT
Z(1)(EET
⊗ HHT
)ZT
(1)G). (30)
tr(Z(1)ZT
(1)) is constant, then the criterion is rewritten by
maximize tr(GT
Z(1)(EET
⊗ HHT
)ZT
(1)G) (31)
subject to GT
G = I, ET
E = I, HT
H = I. (32)
February 2, 2012 15/26

16. Solution Algorithm
Note that
p(G, H, E) :=tr(GT
Z(1)(EET
⊗ HHT
)ZT
(1)G) (33)
=tr(HT
Z(2)(GGT
⊗ EET
)ZT
(2)H) (34)
=tr(ET
Z(3)(HHT
⊗ GGT
)ZT
(3)E). (35)
The image of solution algorithm is described as follows:
Figure: Alternating Least Square(ALS) Algorithm
February 2, 2012 16/26

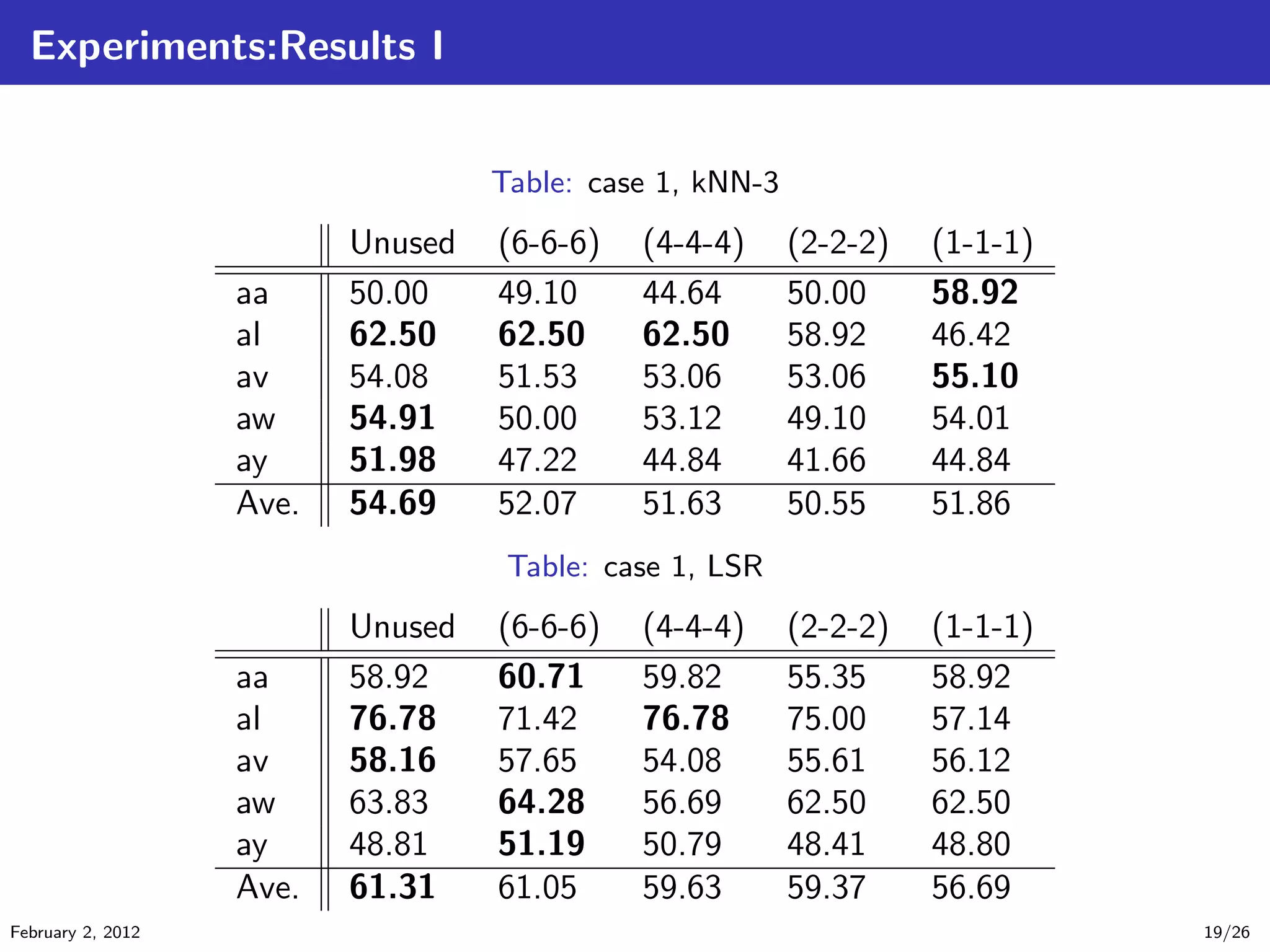
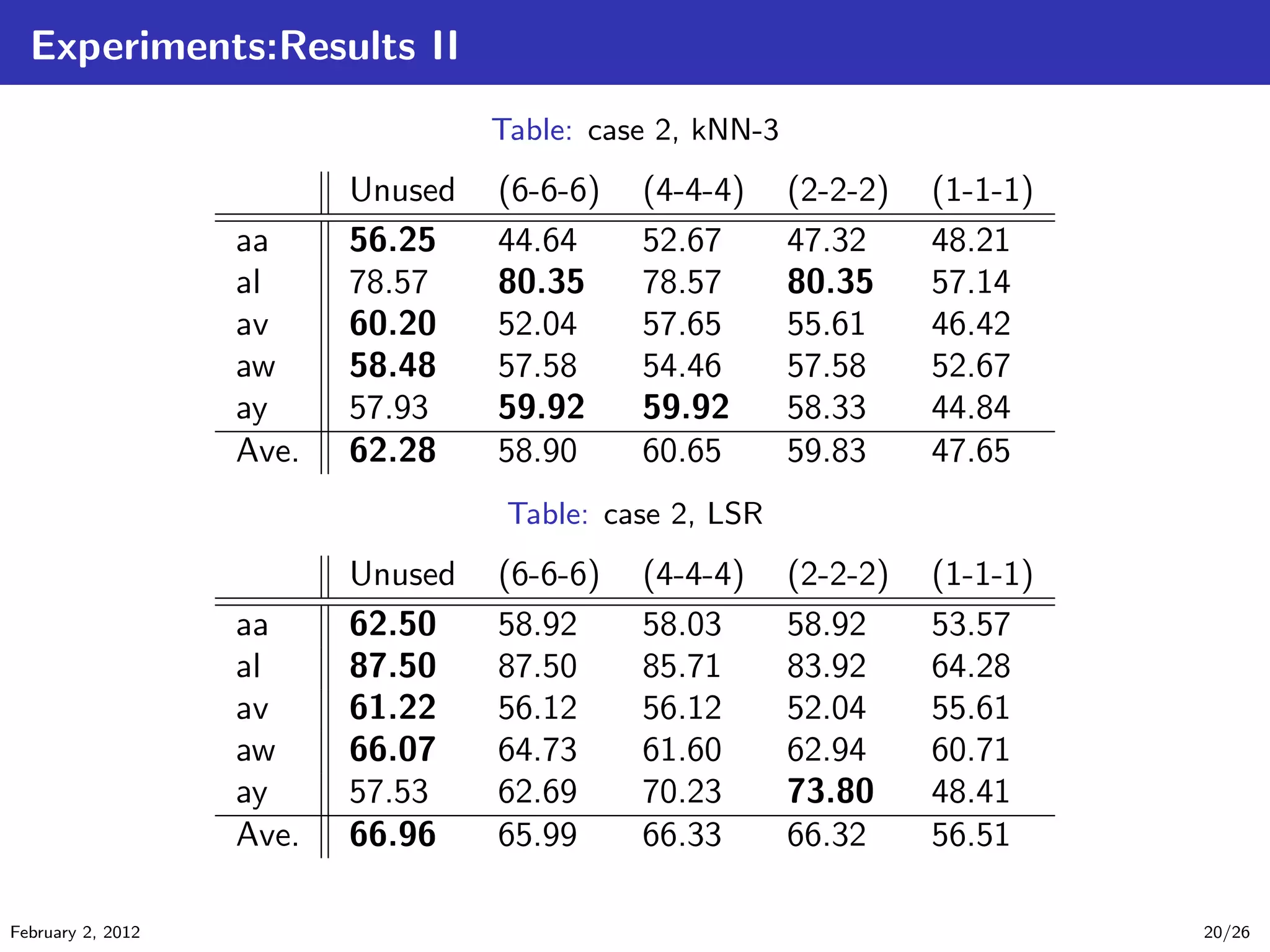
17. Experiments:Data sets [Blankertz, 2005]
.
BCI Competition III : IVa
..
.
. ..
.
.
EEG Motor Imagery Classification data set (right, foot)
There are 5 subjects(aa,al,av,aw,ay)
One imagery for 3.5s
118 EEG channels
Table: Number of Samples
#train #test
aa 168 112
al 224 56
av 84 196
aw 56 224
ay 28 252
-1
-0.5
0
0.5
1
-1 -0.5 0 0.5 1
1
2
3
4
5
6
7 8
9
10
11 12
1314
15
16 17 18 19 20
21
22
23
24 25 26 27 28 29
3031
32
33 34 35 36 37 38 39
40
41
42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58
59 60 61 62 63 64 65 66
67
68
69 70 71 72 73 74 75
76
7778
79 80 81 82 83 84
85
86
87
88
89 90 91 92 93
94
95
9697
98
99 100
101
102103
104105106107108
109110 111
112 113 114
115 116
117 118
February 2, 2012 17/26

18. Experiments:Procedure
...1 Transformation into CMOR domain (time × frequency × channels ×
samples)
CMOR 6-1 (case 1, case 2, case 3)
...2 Applying Dimensionality Reduction
Unused
PCA (6-6-6,4-4-4,2-2-2,1-1-1)
...3 Classification
K-Nearest Neighbor method
Least Squares Regression (Kernel regression)
time frame frequency channels samples # of elements
case 1 35(0:0.1:3.5) 23(8:30) 118 280 26597200
case 2 350(0:0.01:3.5) 23(8:30) 7(51:57) 280 15778000
case 3 35(0:0.1:3.5) 23(8:30) 7(51:57) 280 1577800
February 2, 2012 18/26

19. Experiments:Results I
Table: case 1, kNN-3
Unused (6-6-6) (4-4-4) (2-2-2) (1-1-1)
aa 50.00 49.10 44.64 50.00 58.92
al 62.50 62.50 62.50 58.92 46.42
av 54.08 51.53 53.06 53.06 55.10
aw 54.91 50.00 53.12 49.10 54.01
ay 51.98 47.22 44.84 41.66 44.84
Ave. 54.69 52.07 51.63 50.55 51.86
Table: case 1, LSR
Unused (6-6-6) (4-4-4) (2-2-2) (1-1-1)
aa 58.92 60.71 59.82 55.35 58.92
al 76.78 71.42 76.78 75.00 57.14
av 58.16 57.65 54.08 55.61 56.12
aw 63.83 64.28 56.69 62.50 62.50
ay 48.81 51.19 50.79 48.41 48.80
Ave. 61.31 61.05 59.63 59.37 56.69
February 2, 2012 19/26

20. Experiments:Results II
Table: case 2, kNN-3
Unused (6-6-6) (4-4-4) (2-2-2) (1-1-1)
aa 56.25 44.64 52.67 47.32 48.21
al 78.57 80.35 78.57 80.35 57.14
av 60.20 52.04 57.65 55.61 46.42
aw 58.48 57.58 54.46 57.58 52.67
ay 57.93 59.92 59.92 58.33 44.84
Ave. 62.28 58.90 60.65 59.83 47.65
Table: case 2, LSR
Unused (6-6-6) (4-4-4) (2-2-2) (1-1-1)
aa 62.50 58.92 58.03 58.92 53.57
al 87.50 87.50 85.71 83.92 64.28
av 61.22 56.12 56.12 52.04 55.61
aw 66.07 64.73 61.60 62.94 60.71
ay 57.53 62.69 70.23 73.80 48.41
Ave. 66.96 65.99 66.33 66.32 56.51
February 2, 2012 20/26

21. Experiments:Results III
Table: case 3, kNN-3
Unused (6-6-6) (4-4-4) (2-2-2) (1-1-1)
aa 55.35 50.89 50.00 46.42 44.64
al 78.57 78.57 78.57 78.57 57.14
av 60.20 53.57 55.61 51.02 50.00
aw 57.14 55.35 54.01 57.58 51.78
ay 58.33 58.33 59.52 56.34 44.64
Ave. 61.91 59.34 59.54 57.98 49.64
Table: case 3, LSR
Unused (6-6-6) (4-4-4) (2-2-2) (1-1-1)
aa 57.14 60.71 55.35 56.25 51.78
al 87.50 85.71 85.71 83.92 60.71
av 59.18 55.61 54.08 54.08 53.06
aw 66.07 63.39 58.03 62.50 60.26
ay 57.53 57.93 61.11 63.88 48.41
Ave. 65.48 64.67 62.85 64.12 54.84
February 2, 2012 21/26

22. BCI Competition: IVa Ranking
contributor ave. aa al av aw ay
1 Yijun Wang 94.74 95.5 100 80.6 100 97.6
2 Yuanqing Li 87.40 89.3 98.2 76.5 92.4 80.6
3 Liu Yang 84.54 82.1 94.6 70.4 87.5 88.1
4 Zhou Zongtan 77.24 83.9 100 63.3 50.9 88.1
5 Michael Bensch 74.14 73.2 96.4 70.4 79.9 50.8
6 Codric Simon 73.28 83.0 91.1 50.0 87.9 54.4
7 Elly Gysels 72.36 69.6 96.4 64.3 69.6 61.9
8 Carmen Viduarre 69.62 66.1 100 63.3 64.3 54.4
9 Le Song 69.00 66.1 92.9 67.3 68.3 50.4
10 Ehsan Arbabi 68.26 70.5 94.6 56.1 63.8 56.3
11 Cyrus Shahabi 61.98 57.1 76.8 57.7 64.3 54.0
12 Kiyoung Yang 59.02 52.7 85.7 61.2 51.8 43.7
13 Hyunjin Yoon 53.76 50.0 67.9 52.6 52.7 45.6
14 Wang Feng 52.26 50.9 53.6 54.6 56.2 46.0
My best Result is 66.96% average.
February 2, 2012 22/26

23. Summary
N-way PCA is very efficient for dimensionality reduction.
High dimensional data can be reduced in easily.
In this results, the accuracies almost kept.
However, the accuracies didn’t become good.
EEG classification is very difficult problem.
It is considered that the feature extraction and preprocessing are important.
Especially, channel selection might be very important.
February 2, 2012 23/26

24. Bibliography I
[Blankertz, 2005] Blankertz, B. (2005).
Bci competition iii.
http://www.bbci.de/competition/iii/.
[Cichocki et al., 2009] Cichocki, A., Zdunek, R., Phan, A. H., and Amari, S.
(2009).
Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory
Multi-way Data Analysis.
Wiley.
[Goupillaud et al., 1984] Goupillaud, P., Grossmann, A., and Morlet, J. (1984).
Cycle-octave and related transforms in seismic signal analysis.
Geoexploration, 23(1):85 – 102.
[Henrion, 1994] Henrion, R. (1994).
N-way principal component analysis theory, algorithms and applications.
Chemometrics and Intelligent Laboratory Systems, 25:1–23.
[Hyv¨arinen et al., 2001] Hyv¨arinen, A., Karhunen, J., and Oja, E. (2001).
Independent Component Analysis.
Wiley.
February 2, 2012 24/26

25. Bibliography II
[Kroonenberg and de Leeuw, 1980] Kroonenberg, P. and de Leeuw, J. (1980).
Principal component analysis of three-mode data by means of alternating least
squares algorithms.
Psychometrika, 45:69–97.
February 2, 2012 25/26

26. Thank you for listening
February 2, 2012 26/26