Unit 2 – Probability Distributions (1).pptx

Unit 2 – Probability
Distributions

Probability Distributions
• Before you begin to focus on Probability Distributions, you are advised
to take a few moments and recall the following concepts from Level I
and Lecture 1:
• the concept of a Frequency Distribution arising out of an experiment.
• the concept of a Relative Frequency Distribution arising out of an
experiment.
• the Relative Frequency Approach to Probability and The Axioms of
Probability.
• the definitions of Random Variable, Discrete Random Variable and
Continuous Random Variable

Discrete Probability Distributions
• One definition of a probability distribution for a discrete random variable is
a table that presents all values taken on by the random variable and their
corresponding probabilities. Furthermore, the probabilities sum to one.
• A more comprehensive definition is as follows:
• A probability distribution for a discrete random variable is any table,
function or formula that allows for the following to be presented:
all values taken on by the random variable
their corresponding probabilities.
the probabilities sum to one.

• Steps in the logic of creating a Discrete Probability Distribution:
i. the experiment
ii. the sample space
iii. a sufficiently large number of repetitions of the experiment
iv. the frequency table or distribution of the dataset created
v. the equivalent relative frequency table or distribution
vi. the probability distribution.
• When the relative frequencies are known for the population, these are seen to be
the theoretical probabilities of the outcomes. And the relative frequency table is
seen to be the theoretical probability distribution of the random variable.

• Exercise 1: Each of the tables below lists certain values x of a discrete
random variable X. Determine whether or not each table is a valid
probability distribution.
Table 1 Table 2 Table 3
x P(x) x P(x) x P(x)
1 .08 1 .15 7 .70
2 .22 2 .34 8 .50
3 .39 3 .28 9 -.20
4 .27 4 .23

• We can proceed to show a chart of the only probability distribution
among the three tables.
• We call such a chart the graph of the probability distribution.

• Exercise 2:Check whether the table below constitutes a Cumulative
Probability Distribution for the above probability Distribution. If so,
construct the corresponding graph.
x P(X  x)
1 0.25
2 0.59
3 0.87
4 1.00
>4 1.00

• We could also write the cumulative distribution from Exercise 2 in
functional form e.g.
• As far as functional/formula type presentations of discrete probability
distributions are concerned, we shall look to the Binomial, Poisson,
Negative Binomial, Uniform and geometric Distributions.

• Exercise 4: A random variable X assumes the values of –1, 0, 1 and 2
only. The probability that X assumes the value x is given by
• What kind of random variable is X?
• Show that the information above constitutes a Probability
Distribution.

Probability Mass Function
• This formula is also known as a probability mass function; f(x)

Properties of Probability Mass Functions
• The function is a probability mass function for a discrete r.v. X, if for
each outcome of :
1.

Expected Value of a Discrete Random Variable
• Recall our game involving the tossing of two ‘fair’ coin from
ECON1005.
• Recall the discrete random variable X and its Probability Distribution
Net Prize (X) Outcome(s) P(X=x)
$2 HH 0.25
$0 TH,HT 0.5
-$2 TT 0.25

• Suppose that we played this game repeatedly, say 4000 times.
• From the probability distribution we can say that:
• Net prize money of -$2 is expected in 25% of the games i.e. in 1000 games
• Net prize money of $0 is expected in 50% of the games i.e. in 2000 games
• Net prize money of $2 is expected in 25% of the games i.e. in 1000 games.
• What then would be our average net prize money?
• Average Net Prize Money = Total Net Prize Money
No. of games played

• Average Net Prize Money = Total Net Prize Money
No. of games played
= 1000 (-$2) + 2000($0) + 1000($2)
4000
• Simplifying we get
= 1 (-$2) + 2($0) + 1($2)
4 4 4
= $0

• If therefore we played the game a large number of times, on average,
we can expect to win nothing (and, by extension, lose nothing).
• The value of $0 so computed is called the expected value E(X) of the
discrete random variable X
• What does this mean?
• It certainly does not mean that a player is guaranteed to win nothing or
lose nothing in one game.
• Rather, some players will win, some will break even and some will lose
but, overall, the winnings of one player will cancel out the losses of
another as the number of games gets sufficiently large.

• Look again at the simplified calculation of E(X). We multiplied each value
of the random variable X by its corresponding probability and summed
the resulting products. Hence we can generalize the formula for
expected value to
• E(X) =  xi P(xi)
• The mean of a discrete random variable is the value that is expected to
occur per repetition, on average, if an experiment is repeated a large
number of times.
• In short, E(X) is called the long run average value of the random variable.
• It is also called the first moment of the random variable about the origin.

• Find the mean of X?

Properties of Expectation
• Let X be any discrete random variable
• If a is a constant then E(a) = a
• If a is a constant then E(aX) = a E(X)
• If b is a constant then
• E(X + b) = E(X) + b
• If a and b are constants then
• E(aX + b) = a E(X) + b
• If X and Y are two distinct random variables then
• E( X + Y) = E(X) + E(Y)
• If g(X) and h(X) are two distinct functions defined on X then
• E[g(X) + h(X)] = E[g(X)] + E[ h(X)]

Variance of a Discrete Random Variable
• E(X) has been shown to be equal to the mean of the random variable.
• Recall: the Mean is a measure of central tendency. It highlights where
the probability distribution of X is centered.
• There should be an associated measure of dispersion for the variable
since the mean alone does not give an adequate description of the
shape of the distribution.
• Variance is that measure.
• It is a measure of how the values of the variable X are spread out or
dispersed from the mean.

Variance of a Discrete Random Variable
• Consider a discrete random variable X taking on values x1 , x2 , x3 , …… xn with
associated probabilities p1 , p2 ,p3 , …… pn
• Thus the Variance can be rewritten as
P1 (x1 - )2
+ P2 (x2 - )2
+ …+ Pn (xn - )2
which simplifies to
 Pi (xi - )2
• It is also called the second moment of the random variable X about its
mean.
• The Standard Deviation of X is the square root of Variance of X

• Find the standard deviation of X?

Properties of Variance
• Let X be any discrete random variable
• If a is a constant then Var(a) = 0
• If a is a constant then
• Var(aX) = a2
Var(X)
• If b is a constant then
• Var (X + b) = Var(X)
• If a and b are constants then
• Var(aX + b) = a2
Var(X)
• If X and Y are two independent random variables then
• Var(X + Y) = Var(X) + Var(Y)
• Var X – Y) = Var(X) + Var(Y)
• Var(aX + bY) = a2
Var(X) + b2
Var(Y) where a and b are constants

Continuous Probability Distributions
• We define the probability distribution for continuous random
variables differently
• Recall that we cannot count the values assumed by a continuous
random variable
• The number of values taken on by the variable in any interval is
infinite.
• Accordingly, we modify the approach used for the discrete random
variables.

The steps in creating a probability distribution for continuous random variable is as
follows;
1. the experiment
2. the sample space
3. a sufficiently large number of repetitions of the experiment
4. the frequency table/distribution of the dataset with the class widths as small as
possible
5. the corresponding relative frequency table/distribution
6. the corresponding relative frequency histogram
7. the corresponding relative frequency polygon
8. The probability density curve

• Recall that the heights of the bars in the relative frequency histogram
sum to 1. And the area under the histogram is 1.

• The relative frequency polygon has an area that approximates the
area of the histogram i.e it is equal to 1.
• The smoothed relative frequency polygon is the area under the
probability density curve. Hence the area under the curve also equals
1.
• The function whose graph is the probability distribution curve is called
the probability density function of the continuous random variable.
• The probability that the continuous random variable lies between any
two given values a and b is given by the area under the probability
density curve bounded by the lines x = a and x = b.

• Hence all probabilities will lie in the range of 0 to 1 inclusive.
• Also, the probability that the random variable will assume all possible intervals equals the entire area
under the curve i.e. an area of 1.
• The axioms of probability hold.
• Hence the probability that the continuous random variable assumes for a single value of X is seen to be
the area of a bar with zero width. i.e. such an area equals zero.
• Hence we refer to
• P( X < x )
• P( X > x )
• P( x1 < X < x2 )
• P(x1 > X > x2 ) What do these areas look like?
• The corresponding cumulative probability distribution function F(x) in the case of continuous random
variables is called the probability distribution function.

Properties of Probability Density Functions
• The function is a probability density function for the continuous r.v. X,
defined over the set of real numbers R, if:
1. for all

The Cumulative Distribution Function
• The c.d.f. F for the continuous r.v. X, with p.d.f is given by:

• Exercise 9: Given that
• Determine K so that f(x) is a probability density function
• Generate its probability distribution function F(x)
• Determine P(2 < X < 3).

Expected Value of Continuous Random
Variable
• Recall the fundamental difference in the characterization of
probability for a continuous variable i.e. it is area under the
probability density curve.
• How then do we find and interpret E(X) for continuous variables?
• In the continuous case we find the centre of gravity (so to speak) of
the area under the probability density curve. What does this mean?
Where f(x) is the probability density function

• Determine the mean of X.

Law of the Unconscious Statistician
• If then
• If X is a discrete r.v. with probability mass function then
• If X is a continuous r.v. with probability density function then

Exercise
• Given that for r.v. :
• If
• Find

Variance of a Continuous Random Variable
• For a continuous random variable X with density function f(x) we
define
• Exercise 11: The rules of expectation are unchanged for discrete &
continuous random variables.
• True/False?

• Determine the standard deviation of this probability distribution.

Moments of a Random Variable
• The rth moment about the origin of a random variable X is written as
E[X r
] and is given by
E[X r
] =  xr
P(x) or  xr
f(x) in the discrete case
Or
• where f(x) is the probability density function of X in the continuous
case.
• This holds for r = 0,1,2,3, …….

• The rth moment about the mean of a random variable X is written as
E[(X - ) r
] and is given by
E[(X - ) r
] =  (x -  )r
P(x) or  (x -  )r
f(x) in the discrete
case
Or
where f(x) is the probability density function of X in the continuous
case.
This holds for r = 0,1,2,3, …….

• Exercise 14:
• Show that E(X) is the first moment of X about the origin.
• Show that Var(X) is the second moment of X about its mean.

Other Usefulness of Moments
• We can use Moments to compute other useful measures that
describe a distribution
• Skewness and Kurtosis are two such measures that describe in
particular the shapes of a distribution
• Skewness uses the 3rd
Moment about the mean
• While Kurtosis which is a measure of ‘tailedness’ uses the 4th
Moment
about the mean

Types of Discrete Probability Distributions
• WELL KNOWN DISCRETE PROBABILITY DISTRIBUTIONS
• The Uniform Distribution
• The Bernoulli Distribution
• The Binomial Distribution
• The Negative Binomial Distribution
• The Poisson Distribution
• The Hypergeometric Distribution.
• For each distribution we aim to identify the following:
• The conditions under which the distribution exists
• The parameters of the probability distribution
• The probability distribution formula/function
• The mean, The variance, representation of the cumulative probability distribution

DISCRETE UNIFORM DISTRIBUTION
• Let X be the discrete uniform random variable.
• X assumes a finite number of values, x1, x2, x3, ……xk , with equal
probabilities.
• For example: in the experiment of tossing a fair die; if we let X be the
score on the face of the die, then X assumes values of 1, 2, 3, 4, 5 & 6.
• Parameter of this distribution = k. What is k?
• P ( X = x) = 1
/k for all x in the set of values [x1, x2, x3, ……xk]
• In the example of the toss of the fair die, the probability of X
assuming any one of the six values is 1
/6.

DISCRETE UNIFORM DISTRIBUTION
• Mean  = 1
/k  xi
• Var (X) = 1
/k  (xi -  ) 2
• Exercise 15: Identify other examples of Discrete Uniform
Distributions?

BERNOULLI DISTRIBUTION
• Let X be the Bernoulli random variable.
• X arises out of a single Bernoulli Process. The Process results in one of
two possible outcomes viz. Success and Failure.
• If we assign the value of ‘1’ to Success and ‘0’ to Failure, then we
would have created the Bernoulli Random Variable X.
• X assumes two possible values viz. 0 or 1.
• Parameter of this distribution = p
• P ( X = 1) = p and P(X = 0 ) = 1 – p

BERNOULLI DISTRIBUTION
• Mean  = E(X) = 1 (p) + 0 (1 – p) = p
• Var (X) = ( 1 – p )2
p + ( 0 – p )2
(1 – p) = p ( 1 – p )
• Exercise 16: Are there any other conditions that constitute a Bernoulli
Process?
• Identify other examples of Bernoulli Distributions?

BERNOULLI PROCESS
1. The experiment consists of repeated trials.
2. Each trial results in an outcome that may be classified as a success or
a failure.
3. The probability of success, denoted by p, remains constant from trial
to trial.
4. The repeated trials are independent.

BINOMIAL DISTRIBUTION
• Let X be the Binomial random variable.
• X arises out of a Bernoulli Experiment i.e a finite number (n) of
repetitions of the same Bernoulli trial or process.
• X is always defined as the number of successes in the n repetitions of
the trial.
• As such X assumes values of 0, 1, 2, ………, n
• Parameters of this distribution are n and p
• P( X = r) = n
C r p r
( 1 – p ) n – r
for r = 0, 1, 2, ………, n

BINOMIAL DISTRIBUTION
• Mean  = E(X) = np
• Var (X) = np( 1 – p) or npq.
• Exercise 17: What conditions constitute a Binomial Process?
• Identify examples of Binomial Distributions.

Exercise
• Each month a company either makes a profit, a loss or breaks-even
with probabilities 0.63,0.21 & 0.16 respectively.
a) Determine the probability that in the next year:
1. The company is profitable for 6 months only?
2. The company does not make a profit for at least 3 months?
b) How many months does the company expect to break-even next
year?

POISSON DISTRIBUTION
• Let X be the Poisson random variable.
• X arises out of a Poisson Process. X is always defined as the number
of occurrences per stated unit of time, space or volume.
• X can assume values of 0, 1, 2, 3, …………….∞
• X possesses a Poisson Distribution; this distribution gives the
probability of a number of occurrences per stated unit of time, space
or volume in terms of .
• Parameter of this distribution = 
• r = 0, 1, 2, 3, …………….∞

POISSON DISTRIBUTION
• Mean  = E(X) = 
• Var (X) = .
• Exercise 18: What conditions constitute a Poisson Process?
• Can you identify examples of Poisson Distributions?

Exercise
• The number of movie tickets sold by a cinema averages 50 per week.
1. Determine the probability that the cinema sells its average number
of tickets next week?
2. Write an expression for the probability that the cinema sells at most
5,000 tickets next year?

NEGATIVE BINOMIAL DISTRIBUTION
• Let X be the Negative Binomial random variable.
• X also arises out of a finite number (n) of repetitions of the same
Bernoulli trial.
• X is always defined as the number of trials required before the kth
success occurs.
• As such X assumes values of k, k + 1, k + 2, ………, n
• Parameters of this distribution are n, p and k.
• P( X = r) = r - 1
C k - 1 p k
( 1 – p ) r – k
for r = k, k + 1, k + 2, ………, n

NEGATIVE BINOMIAL DISTRIBUTION
• Mean  = E(X) = kq/p where q = 1 - p
• Var (X) = kq/p2
• Exercise 19: Identify examples of Negative Binomial Distributions?

GEOMETRIC DISTRIBUTION
• Let X be the Geometric random variable.
• X also arises out of a finite number (n) of repetitions of the same
Bernoulli trial.
• X is always defined as the number of trials required before the first
success occurs.
• As such it is a special case of the Negative Binomial Distribution with k
= 1.

• As such X assumes values of 1, 2, 3, ………,n
•
P( X = r) = p ( 1 – p ) r – 1
for r = 1, 2, 3, ………,n
• Mean  = E(X) = ?
• Var (X) = ?

• As such X assumes values of 1, 2, 3, ………,n
•
P( X = r) = p ( 1 – p ) r – 1
for r = 1, 2, 3, ………,n
• Mean  = E(X) = q/p where q = 1 - p
• Var (X) = q/p2

Example
• The probability that a person living in a certain city owns a dog is
estimated to be 0.3. Find the probability:
1) that the tenth person randomly interviewed in that city is the fifth
one to own a dog.
2) that the seventh person interviewed in that city is the first to own a
dog

POISSON APPROXIMATION TO THE BINOMIAL
DISTRIBUTION
• Both the Poisson Random Variable and the Binomial Random Variable
are discrete in nature.
• In the approximation we wish that the graphs of the two distributions
coincide.
• Accordingly, we want the means to coincide and the variances to
coincide as well.
• Thus from the means np =  and from the variances npq = 

POISSON APPROXIMATION TO THE BINOMIAL
DISTRIBUTION
• Such is possible when q 1.
• Since q = 1 – p then it follows that p  0.
• If np =  ,  is finite, and p  0, it follows that n has to be very
large.
• For practical use, n  20 and np < 5.

Types of Continuous Distributions
WELL KNOWN CONTINUOUS
PROBABILITY DISTRIBUTIONS
• The Continuous Uniform Distribution
• The Exponential Distribution
• The Normal Distribution
• The Student -t Distribution
• The Chi Square Distribution
• The F distribution
• The Gamma Distribution
• The Beta Distribution.
For each distribution we again aim to
identify the following:
• The conditions under which the
distribution exists
• The parameters of the probability
distribution
• The probability density function
• The probability distribution curve
• The mean
• The variance
• The probability distribution function

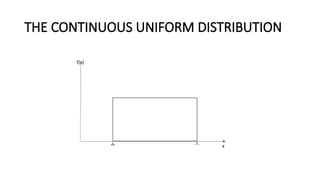
THE CONTINUOUS UNIFORM DISTRIBUTION
• Let X be the continuous uniform random variable.
• Parameters of the distribution are  and .
• X assumes values in the continuous interval of real numbers [ , .]
• The probability distribution curve is rectangular in shape.

f(x)
x
 

• The Probability Density Function f(x) is given by
• for   x  
• Var
• Exercise 21: Can you identify examples of Continuous Uniform
Distributions?

Example
• The r.v. X has a continuous uniform distribution over the interval 0 to
10.
• Find the P(X > 6).

THE NORMAL DISTRIBUTION
• Let X be the normal random variable. X assumes values in the
continuous interval of real numbers [-∞ , +∞]
• Parameters of the distribution are  and .
• The probability distribution curve is bell shaped.
•

•Mean =
•Variance =
• When  = 0 and  = 1 the distribution is called the Standard
Normal Distribution.
• The standard Normal Variable is always denoted by Z.
• Probabilities under the Standard Normal Distribution are provided in
the Standard Normal Table

• Given a random variable X ~ N( , ), by using the transformation
•
• we can establish that P ( a < X < b) = P( z1 , Z < z2) where
• and
• Accordingly, the area in the X distribution that represents P( a < X < b)
equals the area in the Z distribution that represents P( z1 , Z < z2) .
• Any linear combination of normally distributed random variables is
also normally distributed.

• Exercise 22: Identify some examples of Normal Distributions?
• Exercise 23: Look at your copy of the Table of the Standard Normal
Distribution and use it to find some probabilities.
• P(Z < 1.9) P(Z > 2.1)
• P(1.9 < Z < 2.1) P(Z > -1.9)
• P(-1.9 < Z < 1.9) P(Z < -2.1)
• P(0 < Z < 0.44)

Exercise
• Antigua’s annual foreign direct investment has been found to be
normally distributed with a mean of US$12 billion and a standard
deviation of US$2.5 billion. Determine the probability that next year
the country’s foreign direct investment will be between US$10 billion
and US$15 billion.

EXPONENTIAL DISTRIBUTION
• Let X be the Exponential random variable.
• The Exponential Distribution is applicable when conditions of a
Poisson Process are present.
• X is defined as the time between two successive occurrences in a
Poisson Process.
• Parameter of this distribution = 1
/β
• Where β is the average time between two successive occurrences
• X can assume real values greater than or equal to 0.

EXPONENTIAL DISTRIBUTION
• f(x) = 1
/βe –x/β
for x  0
= 0 otherwise.
• Mean =
• Variance =
• Exercise 24: What conditions constitute an Exponential Process?
• Identify examples of Exponential Distributions?

Example
• Based on extensive testing, it is determined that the average time
before a major repair is required for a certain washing machine is 4
years. Determine the probability that the machine requires a major
repair within the first year of purchase.

Normal Approximation To The Binomial
Distribution
• Recall the following:
• Variable Type Mean Variance
• Binomial Discrete np npq
• Normal Continuous μ σ2
• Std Normal Continuous 0 1
• We are seeking to approximate a discrete probability distribution by a continuous one
• What links the Binomial Variable with the Standard Normal Variable?
• The Central Limit Theorem provides the link. The theorem states ….
• If all samples of a fixed size are selected from any population, the sampling
distribution of the sample means is approximately a normal distribution. This
approximation improves with samples of larger size.

Distribution
• Let X be the discrete random variable.X ~ B( n , p )
• If n is large and we performed the following:
• * define for each value x of X the quotient
• * create a frequency distribution of the set of values z and
• * plot a histogram from the frequency distribution.
• We will find that the shape of the histogram is approximately bell shaped.
• Furthermore, the outline of the histogram will approximate the curve of the
Standard Normal Distribution i.e. mean = 0, variance = 1

Distribution
• Hence the Std Normal .
• This is the basis of the approximation.

Methodology for the Approximation
• Let X be a Binomial Variable with parameters n and p.
• How do we estimate P( a ≤ X ≤ b) by a Normal Approximation ?
• Perform the Continuity Correction i.e.
• P( a ≤ X ≤ b) = P( a - .5 < X < b + .5)
• Set up the transformation
• Transform the left hand a – 0.5 to z1
• Transform the right hand b + 0.5 to z2

Methodology for the Approximation
• Sketch a curve of the Std Normal Distribution and shade the area that
corresponds to P( z1 < Z < z2)
• Read off the area from the Standard Normal Table
• Exercise 25: For what values of p and q will the Normal Approximation
yield accurate estimates of the binomial probability?
• Exercise 26: State the Central Limit Theorem
• Exercise 27: Suppose that 75% of the students in an educational
institution are known to be female. When a sample of 100 students is
drawn from the school population, what is the probability that there will
be more than 20 male students in that sample?

Student-t Distribution
• It is a Continuous Distribution
• It possesses one parameter ,  , called its degrees of freedom;  is
always a positive whole number
• The random variable that possesses a t-distribution with  degrees of
freedom is denoted by T and may take on any value on the real line.
• Each different value of  corresponds to a different member of the family
of t-distributions
• The graph of the t-distribution is symmetrical and almost bell-shaped
• As  gets larger, its shape gets closer and closer to that of the standard
normal distribution.

• Since the t-distribution approaches the standard normal distribution as 
increases, the percentiles of the standard normal distribution may be used to
estimate those of the t-distribution.
• Formula for T
• Let {xi , i = 1, 2,…n} be a random sample of size n with standard deviation s
drawn from a normal distribution N (, ).
• The variable T possesses a Student t- distribution with n - 1 degrees of freedom.
• Probabilities for selected values of T are provided in the Student- t Distribution
tables. It is critical that you are familiar with the structure of these tables.

• Exercise 28:
• Use the Table of the Student-t Distribution to compare the
probabilities below for 15, 30, 60 and 120 degrees of freedom
• P(T < 1.9) P(T > 2.1)
• P(1.9 < T < 2.1) P(T > -1.9)

THE CHI SQUARE DISTRIBUTION
• It possesses one parameter,  , called its degrees of freedom;  is always a
positive whole number
• The random variable which possesses a Chi Square distribution with  degrees
of freedom is denoted by and may take only positive values
• Each different value of  corresponds to a different member of the family of Chi
Square distributions
• The graph of the Distribution is uni-modal and right skewed. The skewness
becomes smaller as  increases.
• As  gets larger, its shape gets closer and closer to that of the standard normal
distribution.

THE CHI SQUARE DISTRIBUTION
• The probability density function of
•
• Where is the gamma function
• Var
• Exercise 29: Use the Table of the Chi Square Distribution to compare
the probabilities below for 15, 30, 60 and 100 degrees of freedom
• P(2
< 14) P(2
> 19)

The F Distribution
• It possesses two parameters 1 and 2 called its degrees of
freedom; 1 and 2 are always positive whole numbers
• The random variable which possesses an F distribution with 1 and
2 degrees of freedom is denoted by F(1 , 2) and may take only
positive real number values.
• Each pair of values of 1 and 2 corresponds to a different member
of the family of F distributions
• The graph of the F distribution is unimodal and right skewed.

The F Distribution
• Let U and V be two independent random variables having chi-squared
distributions with v1 and v2 degrees of freedom, respectively. Then
the random variable follows the F distribution with p.d.f.
•
• Where is the gamma function

The F Distribution
• E (F(1 , 2 )) = 2/(2-2) when 2 > 2
• V(F(1 , 2)) = 22
2
((1 + 2 - 2))/ (1)( 2 – 2)2
(2 - 4) when 2 > 4.
• It is undefined for 2 < 4.
• As 2  , the expression for the mean tends to 1 while the variance approaches
zero as both degrees of freedom become large.
• Define F( a : 1 , 2) & Define F( 1 - a: 2 , 1)
• Note that F( a : 1 , 2) = [F( 1 - a: 2 , 1)] –1
• Exercise 30: Use the Table of the F Distribution to compare the probabilities below
for (4,15) and (30,7) degrees of freedom
• P(F < 1.8) P( F > 2.4)

Unit 2 – Probability Distributions (1).pptx

More Related Content

Similar to Unit 2 – Probability Distributions (1).pptx

More from giovanniealvarez1

Recently uploaded

Unit 2 – Probability Distributions (1).pptx