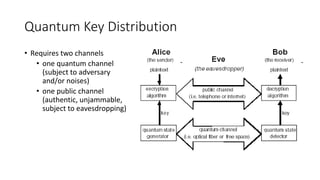
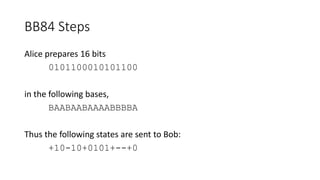
Quantum cryptography leverages quantum mechanical properties for cryptographic tasks, exemplified by quantum key distribution (QKD), which ensures secure key exchange despite eavesdropping. The process involves Alice sending photons of random polarizations to Bob, who measures them, while any eavesdropping can be detected through increased error rates. While quantum cryptography presents promising security benefits, its high cost and limitations, such as short transmission distances, prevent widespread adoption in the near future.

1. Quantum Cryptography
Sreekanth N|Pgdbt201815

2. Introduction
• Quantum cryptography is the science of exploiting quantum mechanical
properties to perform cryptographic tasks.
• The best known example of quantum cryptography is quantum key
distribution which offers an information-theoretically secure solution to
the key exchange problem.
• The advantage lies in the fact that it allows the completion of various
cryptographic tasks that are proven or conjectured to be impossible using
only classical communication.
• It is impossible to copy data encoded in a quantum state. If one attempts to
read the encoded data, the quantum state will be changed
• This could be used to detect eavesdropping in quantum key distribution.

3. Why Quantum computing?
• Conventional cryptosystem:
• Alice and Bob share N random bits b1…bN
• Alice encrypt her message m1,…,mN ~~ b1*m1,…,bN*mN
• Alice send the encrypted string to Bob
• Bob decrypts the message: (mj#bj)#bj = mj
• As long as b is unknown, this is secure
• Classical cryptography techniques allow the key transmission to be
passively monitored without alerting the legitimate users.
• Quantum computing and mathematical advances may soon render
current cipher algorithms obsolete.

4. Quantum computing – Polarized photons
• Light waves are propagated as discrete particles
known as photons.
• Polarization of the light is carried by the direction of
the angular momentum, or spin of the photons.
• Polarization can be modeled as a linear combination
of basis vectors vertical () and horizontal ()
• A quantum state of a photon is described as a vector
• quantum cryptography often uses photons in 1 of 4
polarizations (in degrees): 0, 45, 90, 135


ψb
a

5. Quantum computing – A polarization filter
Unpolarized
light
Vertical
aligned filter
Vertically
polarized light Filter tilted at
angle q
• A polarization filter is a material that allows only light of a specified
polarization direction to pass.
• A photon will either pass or not pass through a polarization filter, but
if it emerges it will be aligned with the filter regardless of its initial
state. There are no partial photons.

6. Quantum Key Distribution - BB84 Protocol
• It’s NOT a new crypto algorithm!
• Two physically separated parties can create and share random secret
keys.
• Allows them to verify that the key has not been intercepted.
• Requires two channels
• one quantum channel (subject to adversary and/or noises)
• one public channel (authentic, unjammable, subject to eavesdropping)

7. Quantum Key Distribution
• Requires two channels
• one quantum channel
(subject to adversary
and/or noises)
• one public channel
(authentic, unjammable,
subject to eavesdropping)

8. Quantum Cryptosystem : Basic Operation
• Alice transmits short bursts. The polarization in each burst is
randomly modulated to one of four states (horizontal, vertical, left-
circular, or right-circular).
• Bob measures photon polarizations in a random sequence of bases
(rectilinear or diagonal).
• Bob tells the sender publicly what sequence of bases were used.
• Alice tells the receiver publicly which bases were correctly chosen.

9. Quantum Cryptosystem : Basic Operation
• Alice and Bob discard all observations not from these correctly-
chosen bases.
• The observations are interpreted using a binary scheme: left-circular
or horizontal is 0, and right-circular or vertical is 1.

10. BB84 Steps
• Set-up
• Alice
• Has the ability to create qubits in two orthogonal bases
• Bob
• Has the ability to measure qubits in those two bases.

11. BB84 Steps
• Alice
• Encodes her information randomly in one of the two bases…
• For example,
Basis A Basis B
ￜ0〉= 0 ￜ+〉= 0
ￜ1〉= 1 ￜ-〉= 1

12. BB84 Steps
Alice prepares 16 bits
0101100010101100
in the following bases,
BAABAABAAAABBBBA
Thus the following states are sent to Bob:
+10-10+0101+--+0

13. BB84 Steps
Bob receives the stream of qubits and measures each one in a
random basis:
ABAABAAABABBBBAB
Alice’s bits 0101100010101100
Alice’s bases BAABAABAAAABBBBA
States sent +10-10+0101+--+0

14. BB84 Steps
So Bob gets
1-00-0+0+0-+--1+

15. BB84 Steps
Then Alice and Bob compare their measurement bases, not
the results, via a public channel.

16. BB84 Steps
• So Bob and Alice are left with 7 useable bits out of 16
_ _ 0 _ _ 0 _ 0 _ 0_ 0 1 1 _ _
These bits will be the shared key they use for encryption.

17. Detecting an Eavesdropper (no-cloning
theorem)
• Heisenberg’s uncertainty principle states that there are certain
conjugate variables on which limits are placed on the simultaneous
knowledge of both.
• No-cloning theorem - it is impossible to create an identical copy of an
arbitrary unknown quantum state. Measuring one variable will
necessarily affect the other.
• Polarization properties of light fall into this category, therefore, an
intruder who is trying to intercept and measure the optical signal will
invariably affect the system in a such a way that their interference will
be noticed.

18. Detecting an Eavesdropper
So how do we know when Eve is listening?
• Well… Eve doesn’t know what bases to measure in, so she would
have to measure randomly and 50% of the time she will be wrong…
• Thus, of the bits Bob measures in the correct bases, there is 50% that
eve had changed the basis of the bit. And thus it is equally likely that
Bob measure 0 or 1 and thus an error is detected 25% of the time.
• Eve is found in the errors!

19. BB84
• In a world with perfect transmissions, all Bob and Alice have to do is
publicly compare a few bits to determine if any error exists.
• Errors exist in reality, thus the only way to detect Eve is to notice an
increase in errors.
• Thus the transmission process must not have an error rate higher
than 25%.

20. Commercial QC
• There are currently four companies offering commercial quantum key
distribution systems
• ID Quantique (Geneva)
• MagiQ Technologies, Inc. (New York)
• QuintessenceLabs (Australia) and
• SeQureNet (Paris)
• Qubitekk
• Several other companies also have active research programs,
including Toshiba, HP, IBM, Mitsubishi, NEC and NTT

22. Commercial QC
• In 2004, the world's first bank transfer using quantum key distribution
was carried out in Vienna, Austria.
• Quantum encryption technology provided by the Swiss company Id
Quantique was used in the Swiss canton of Geneva to transmit ballot
results to the capital in the national election occurring on 21 October
2007.
• In 2013, Battelle Memorial Institute installed a QKD system built by ID
Quantique between their main campus in Columbus, Ohio and their
manufacturing facility in nearby Dublin.

23. Pros
• Nearly Impossible to steal
• Detect if someone is listening
• “Secure”

24. Weaknesses and Limitations of Q C
•Only works along unbroken and relatively short fiber optic cables.
Record as of March, 2004 is 120 km.
•Doesn’t solve authentication problem.
•Doesn’t address some of the weakest links in data security such as
human corruptibility and key storage.
•Relatively high cost.
• Vulnerable to DOS

25. Conclusion
• Quantum cryptography developments promise to address some of
the problems that plague classical encryption techniques such as the
key distribution problem and the predicted breakdown of the
public/private key system.
• Quantum cryptography operates on the Heisenberg uncertainty
principle and random polarization of light.
• Due to the high cost of implementation and the adequacy of current
cryptological methods, it is unlikely that quantum cryptography will
be in widespread use for several years.