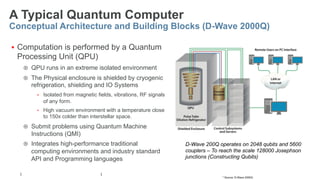
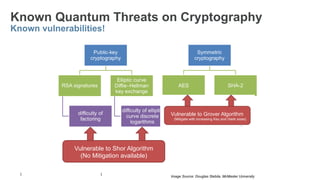
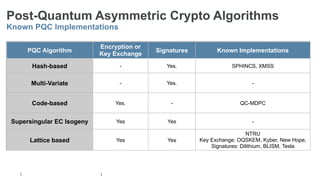
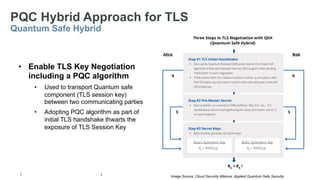
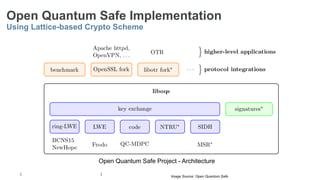
The document provides a comprehensive overview of post-quantum cryptography, comparing classical and quantum computing, and highlighting the vulnerabilities traditional encryption faces against quantum algorithms like Shor's and Grover's. It discusses the need for post-quantum cryptography (PQC) and quantum key distribution (QKD) as methods to secure communications against quantum attacks, detailing various quantum-resistant algorithms. Additionally, it reviews ongoing efforts for standardization in the realm of post-quantum cryptography through initiatives by NIST and ETSI.

1. Post Quantum Cryptography: Technical Overview
Quantum-resistant Cryptography, Implementations and Strategies
Ramesh Nagappan

2. Digital Computing vs. Quantum Computing
Comparison of Classical Computers vs. Quantum Computers
§ Classical Computers
¤ Built upon the notion of digital logic,
digital signals using bits
• Encodes information in a series of bits and
performs operations using logical gates.
• Bits are represented using discrete binary
values “0” or “1”
¤ Embodied by transistors (charged “1” or
uncharged “0”) and circuits implemented
using CMOS (Metal oxide semiconductor)
• Operates using a Microprocessor
determines how many operations can be
carried out in a given time (Clock speed)
• Performs computing operations
sequentially
• Operations are defined and
performed using Boolean algebra
§ Quantum Computers
¤ Envisioned by Richard Feynman in 1980s
¤ Exploits quantum theory and behavior of particles at
atomic and sub-atomic level
• Bit of data represented by a single atom using Qubit
• Qubits can use two states and a superposition of the two
states and its quantum correlations
• Encoded as 1 and 0 and simultaneously (superposition and
entanglement)
• Quantum effects (Superposition, Entanglement and
Quantum tunneling)
• Performs operations in parallel using quantum effects
(Processing using Quantum gates)
¤ Operates in an extreme Cryogenic environment
• 150x colder than interstellar space and Low pressure
(10B times lower than atmosphere)
• Shielded 50,000x less than Earth’s magnetic field
* Source: D-Wave 2000Q

3. A Typical Quantum Computer
Conceptual Architecture and Building Blocks (D-Wave 2000Q)
§ Computation is performed by a Quantum
Processing Unit (QPU)
¤ QPU runs in an extreme isolated environment
¤ The Physical enclosure is shielded by cryogenic
refrigeration, shielding and IO Systems
• Isolated from magnetic fields, vibrations, RF signals
of any form.
• High vacuum environment with a temperature close
to 150x colder than interstellar space.
¤ Submit problems using Quantum Machine
Instructions (QMI)
¤ Integrates high-performance traditional
computing environments and industry standard
API and Programming languages
D-Wave 200Q operates on 2048 qubits and 5600
couplers – To reach the scale 128000 Josephson
junctions (Constructing Qubits)
* Source: D-Wave 2000Q

4. Quantum Algorithms
The importance of Shor and Grover Algorithms
þ Quantum algorithms are intended to model and perform Quantum computation
⦿ Consists of quantum gates and acts on fixed number of Qubits
⦿ Inherits quantum effects such as Superposition and Entanglement to perform faster and
parallel computations
⦿ Acts on input qubits and exits on solving a problem
• Quantum algorithms use Quantum Fourier transform, which is analogous to discrete Fourier transform
• Examples: Deutsch-Josza, Simon, Shor, Grover, Boson sampling, Fourier fishing and Fourier checking
þ Shor’s algorithm (Prof. Peter Shor of MIT)
⦿ Solves discrete logarithm problems amd integer factorizations in a polynomial time.
þ Grover’s algorithm (Prof. Lov Kumar Grover of Cornell University)
¤ Searching unstructured entries on a database for a marked entry and allows faster querying of
results.

5. Known Threats of Quantum Algorithms
Quantum Cryptanalysis!
þ Traditional Public-key Cryptosystems (RSA, ECC, DSA) are breakable by Shor’s algorithm
¤ Shor’s algorithm efficiently solves integer factorizations and discrete algorithms leads to breaking
asymmetric cryptographic schemes.
¤ Any adversary who sniffs and records a public-key encrypted communication would able to easily
decrypt the recording using a quantum computer. (Communication Harvesting attack).
¤ Increasing key size or changing parameters does not mitigate the exposure.
þ Symmetric key encryption and Hashing functions can potentially broken by brute force
using Grover’s algorithm
¤ Gives a square-root speedup on key searching over symmetric key algorithms and searching for
preimages and collisions by a cube-factor on hashing functions.
¤ For example, AES128 requiring 2256 operations can be compromised by 264 operations on a
quantum computer.
¤ Doubling or increasing key and hash value sizes can help mitigate and requires constant update as
quantum computer evolves.

6. Image Source: Douglas Stebila, McMaster University
Known Quantum Threats on Cryptography
Known vulnerabilities!
Vulnerable to Shor Algorithm
(No Mitigation available)
Vulnerable to Grover Algorithm
(Mitigate with increasing Key and Hash sizes)

7. Known Quantum Threats on Cryptography
Real-world Applications potentially broken by Quantum Computing
1. Secure Network Communication including Virtual Private Networks
(VPN)
2. Secure Email Communications using S/MIME protocols
3. Web Applications Security using SSL/TLS (including TLS 1.2, TLS 1.3)
4. Identity Federation and XML Web Services (including XML Encryption and XML
Signatures)
5. Public Key Infrastructure and Certificate Authorities (PKI Lifecycle operations)
6. Digital signatures in electronic transactions (Identity of electronic transactions)
7. Software and Mobile App distribution
8. Cloud Virtual Machine images from Marketplace (Image authenticity and integrity)
9. Blockchain applications (Private Key derivation and Signatures)
Image Source: Google

8. Image Source: MIT Technology Review (2017)
Known Quantum Threats on Blockchain
Private Key derivation vulnerability!

9. Post-Quantum Cryptography & Quantum Key Distribution
Two different efforts – Why both are not the same?
§ Post-Quantum Cryptography
(PQC)
¤ Traditional cryptographic schemes
deployable on classical computers
and known to be quantum-resistant.
¤ Assures mathematical hardness
when compared with public-key
cryptosystems
¤ Security against quantum attacks
and impacts of Grover’s and Shor’s
algorithms.
§ Quantum Key Distribution (QKD)
¤ Secure communication using Quantum
superposition and entanglements.
• Encoding information in quantum states and
transmission of particles (Over a Physical
Quantum channel
• Generate and secure distribution of keys (Over
a QKD link)
¤ QKD is not based on traditional
computations – It is intrinsically sage
• Not vulnerable to Shor and Grover.

10. Image Source: Douglas Stebila, McMaster University
Post Quantum Cryptography
Quantum Safe against Shor and Grover algorithms

11. Post-Quantum Asymmetric Crypto Algorithms
Quantum-resistant Crypto schemes without factorization and discrete logarithms
þ Lattice-based Cryptography
¤ Proposed by M.Ajtai 1996, one of the early cryptographic schemes relied on the hardness of
computational lattice problems
¤ In 2005, Regev introduced the Learning With Errors (LWE) based on Lattice problem which serves as
the basis for a variety of public-key encryption and signature schemes
¤ Following LWE, in 2010, Lyubashevsky, Peikert, and Regev introduced the Ring-Learning With Errors
(Ring-LWE) which used an additional structure that allows for smaller key sizes.
þ Multi-variate Cryptography
¤ Based on the difficulty of solving non-linear usually quadratic, polynomial over a finite field.
¤ The hardness of the system depends on the size of the finite field, variables and the degree of the
system. .
¤ For building asymmetric public key system, the public key is a set of multivariate quadratic
polynomials and the private key is the knowledge of a trapdoor that allows solving the multi-variate
system.

12. Post-Quantum Asymmetric Crypto Algorithms.. contd
Quantum-resistant Crypto schemes without factorization and discrete logarithms
þ Code-based Cryptography
¤ Based on McEliece public key encryption that uses error correcting codes to hide contents of a
message during transmission on an unreliable channel.
¤ The message sender deliberately adds an error in order to protect the contents of a message against
an eavesdropper.
þ Hash-based Cryptography
¤ Based on Lamport, Diffie, and Winternitz who demonstrated how to convert Merkle’s one-time
signature scheme into a many-time signature scheme.
¤ Although there is a security issue with statefulness requiring the re-usage of private key material and
during backups (data loss). The new variants SPHINCS and XMSS are considered quantum-
resistant, which allows stateless schemes with larger signature sizes.
þ Supersingular Elliptic-Curve Isogeny
¤ Using difficulty in finding isogenies between supersingular elliptic curves. They have a similar
structure to classical Diffie-Hellman and ECDH approaches.

13. Post-Quantum Asymmetric Crypto Algorithms
Known PQC Implementations
.
PQC Algorithm
Encryption or
Key Exchange
Signatures Known Implementations
Hash-based - Yes. SPHINCS, XMSS
Multi-Variate - Yes. -
Code-based Yes. - QC-MDPC
Supersingular EC Isogeny Yes Yes -
Lattice based Yes Yes
NTRU
Key Exchange: OQSKEM, Kyber, New Hope,
Signatures: Dilithium, BLISM, Tesla

14. Lattice-based Cryptography
Usage Scenarios and PQC approaches
.
§ Most active field of research and several implementations
available.
¤ NTRU Public-key Cryptosystem: Encryption/Decryption and Digital signatures.
¤ Kyber: Secure key encapsulation mechanism (KEM), based on solving the learning-
with-errors (LWE) problem over module lattices. (Under NIST review)
¤ New Hope: Simple key exchange based on Ring-LWE. (Under NIST review)
¤ Frodo: Key Exchange based on LWE.
¤ Signatures: Dilithium, Bliss, and Tesla

15. Lattice-based Key Encapsulation Mechanism (KEM)
Usage Scenario
.
§ Key Encapsulation Mechanism (KEM) Scenario
– The receiver generates a public and private key pair.
– The receiver publishes the public key but keeps the private key secret.
– A sender obtains the public key.
– That sender uses encapsulate to obtain a ciphertext and shared key.
– That sender sends the ciphertext to the receiver.
– The receiver obtains the ciphertext.
– The receiver uses decapsulate on the ciphertext to obtain the shared key (for
symmetric key encryption)
§ Kyber: Module-lattice based KEM (128-bit and 224-bit Quantum security)

16. Hybrid Approaches
Easy Retooling: Known devils are better than unknowns
.
§ Use Pre-Quantum/Traditional algorithms and PQC algorithms together
– Use Hybrid ciphersuites involving one traditional public-key algorithm and one
PQC algorithm
– Reduce risks from uncertainty if either one of them is broken
– Maintain compliance with older standards and use of validation (FIPS 140-2)
§ Adopt Hybrid ciphersuites involving one traditional public-key
algorithm and one PQC algorithm
¤ For Key exchange: Both communicating parties would establish two shared secrets – Using
one traditional Key exchange scheme and one PQC based Key exchange scheme.
¤ Kyber, New Hope, OQSKEM makes it compelling as it can be used as ephemeral key
exchange.
¤ For example: In a TLS scenario, the TLS handshake use two key exchange algorithm – ECDH (Traditional) and New Hope (PQC)

17. Image Source: Cloud Security Alliance: Applied Quantum Safe Security
PQC Hybrid Approach for TLS
Quantum Safe Hybrid
• Enable TLS Key Negotiation
including a PQC algorithm
• Used to transport Quantum safe
component (TLS session key)
between two communicating parties
• Adopting PQC algorithm as part of
initial TLS handshake thwarts the
exposure of TLS Session Key

18. Quantum Safe: Digital Certificates
Post-Quantum PKI Server using Quantum Safe Digital Signature Schemes
.
§ Demonstrates the viability of PQC Hybrid X.509 certificates
§ PQ Hybrid Certificate include extensions to support PQC algorithms
– Adding Public Key and Signature algorithms (LMS, SPHINCS)
§ Entities making use of PQ algorithms in the Certificate extensions can verify
PQ Key and signature
¤ Test Opensource implementation available at http://test-pqpki.com
¤ Under review by NIST Post-Quantum Crypto Project -
https://csrc.nist.gov/Projects/Post-Quantum-Cryptography

19. Open Quantum Safe Project
https://openquantumsafe.org
.
• Development and Prototyping Quantum-resistant Cryptography adhering to
NIST Post-Quantum Cryptography Standardization Project
• Open-source C library with multiple PQ key exchange algorithms and PQ
signatures (soon) and integrations into protocols and applications
Ø Integrations available for OpenSSL and OpenSSH
Ø TLS 1.2 prototype and available as a fork for OpenSSL
Ø TLS 1.3 prototype later this year

20. Open Quantum Safe Implementation
Using Lattice-based Crypto Scheme
.
Open Quantum Safe Project - Architecture
Image Source: Open Quantum Safe

21. NSA IAD and EU: Call for Action
Role of NIST and ETSI
§ NIST Started Quantum Resistant Crypto Standardization
Group
– Announced competition for Post-Quantum Crypto Algorithms and receiving
submissions
§ ETSI established Quantum Safe Crypto (QSC) Group
– H2020 projects (SAFE Crypto, PQCrypto)
Image Source: NSA, NIST, ETSI

22. References/Citations
§ MIT Technology Review: QKD 2017
§ Topics in Cryptology CT-RSA 2018 (Springer Press)
§ M.Grassl, B.Langenberg, M.Roetteer and R.Steinwandt – Applying Grover’s Algorithm to
AES: Quantum Resource Estimates – PQCrypto 2016
§ M Waidner, R. Niederhagen, T.Grotker, P. Reinelt – Post-Quantum Crypto
§ D.Stebila and M. Mosca – Post-Quantum Key Exchange for the Internet and the Open
Quantum Safe Project
§ D-Wave Systems - 2000Q System (dwavesys.com)
§ Cloud Security Alliance: Quantum Safe Security
§ ISARA : Quantum Safe PKI and Certificates (isara.com)
§ University of Waterloo: Quantum Computing Resources
§ Ramesh Nagappan Blog: http://www.websecuritypatterns.com