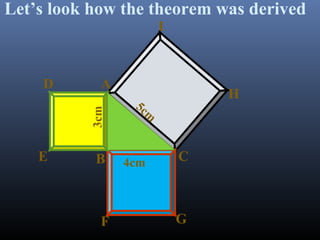
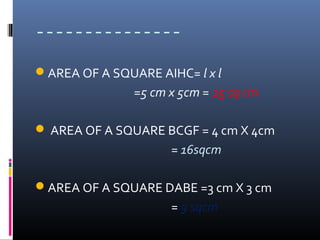
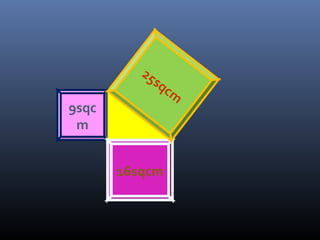
The document discusses Pythagoras, a Greek philosopher born around 570 BC, and his contributions to mathematics, philosophy, and the establishment of a school in Croton. It explains the Pythagorean theorem, stating that in a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides. Examples illustrate how to apply the theorem to find the lengths of triangle sides.

1. Class:VII

2. About Pythagoras
Pythagoras was born in the island of Samos in
ancient Greece . There is no certainty regarding the
exact year when he was born, but it is believed that
it was around 570 BC That is about 2,570 years ago!

3. About Pythagoras
(cont…)
 At Croton he started a school which
concentrated in the teaching and learning of
Mathematics, Music, Philosophy, and
Astronomy and their relationship with
Religion.
 He emphasized justice based on equality.
Calmness and gentleness were principles
encouraged at the school.

4. Lets study the Pythagoras Theorem
a2 b2 c2
hypotenuse
side
side
a
b
c

5. Let’s look how the theorem was derived
3cm
5cm
4cm
A
B C
D
E
F G
H
I

6. ---------------
AREA OF A SQUARE AIHC= l x l
=5 cm x 5cm = 25 sq cm
 AREA OF A SQUARE BCGF = 4 cm X 4cm
= 16sqcm
AREA OF A SQUARE DABE =3 cm X 3 cm
= 9 sqcm

7. 9sqc
m
25sqcm
16sqcm

8. Therefore……
In a right angled triangle , the area of the square on the
hypotenuse is equal to the sum of areas of the squares on
the remaining two sides.
(Hypotenuse)2 (side 1)2 (side 2)2

9. EXAMPLE…..
The length of the sides forming the right angled of a right
angled triangle are 6 m and 8 m . Find the hypotenuse.
According to Pythagoras theorem , ?
(Hypotenuse)2 = (side1)2 + (side2)2
6 m
8 m
= (6m)2 + (8 m)2
= 36sqm + 64sqm
= 100sqm
Hypotenuse = (10 m)2
(hypotenuse)2 = 100 m2
Hypotenuse = 10m

10. 15cm
9cm
?
In the alongside figure the
hypotenuse and one side of the
right angle is given .
Find the length of the other side.
(hypotenuse)2 = (side1)2 + (side2)2
(15 cm)2 = (9 cm)2 + (second side)2
225 sqcm= 81sqcm + (second side)2
225 sqcm – 81sqcm = (second side)2
144 sqcm = (second side)2
(12cm)2 = (second side)2
12cm = second side