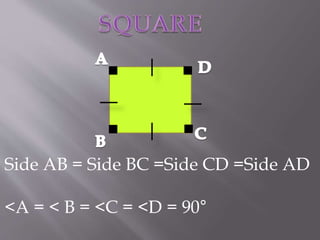
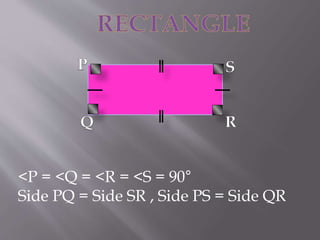
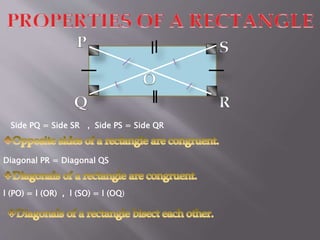
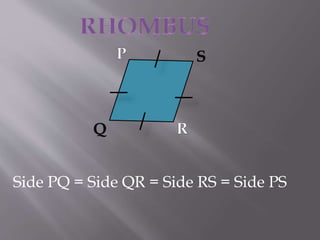
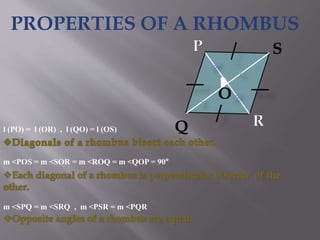
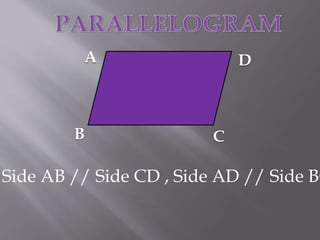
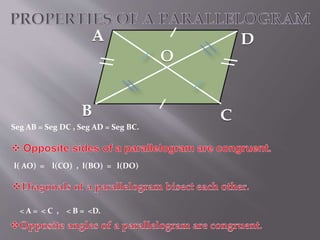
The document explains the definition and properties of various types of quadrilaterals, including squares, rectangles, rhombuses, and parallelograms. Each shape is characterized by specific properties regarding sides, angles, and diagonals. It also includes evaluation questions related to the concepts presented.

2. NEGATIVE EXAMPLES POSITIVE EXAMPLES

3. TYPES OF
QUADRILATERALS

4. • The origin of the word “quadrilateral” is the
two latin words
quadr i - a variant of four
&
• latus – side
• A closed four sided figure is called a quadrilateral
• A quadrilateral is a polygon that has exactly
four sides, exactly
four vertices & exactly four angles.

5. RECTANGLE
TRAPEZIUM
PARALLELOGRAM
SQUARE
RHOMBUS

6. Side AB = Side BC =Side CD =Side AD
<A = < B = <C = <D = 90°

7. A quadrilateral with all sides
congruent and each angle a
right angle is called a square.

8. l (AC) = l (BD)
l (AO) = l (OC) , l (BO) = l (OD)
m <AOD = m <DOC = m <BOC = m <BOA = 90°

9. <P = <Q = <R = <S = 90°
Side PQ = Side SR , Side PS = Side QR

10. A quadrilateral with each angle
a right angle and opposite sides
congruent is called a rectangle.

11. Side PQ = Side SR , Side PS = Side QR
Diagonal PR = Diagonal QS
l (PO) = l (OR) , l (SO) = l (OQ)

12. Side PQ = Side QR = Side RS = Side PS

13. A quadrilateral having all
sides congruent is called a
rhombus.

14. PROPERTIES OF A RHOMBUS
l (PO) = l (OR) , l (QO) = l (OS)
m <POS = m <SOR = m <ROQ = m <QOP = 90°
m <SPQ = m <SRQ , m <PSR = m <PQR

15. B
D
C
Side AB // Side CD , Side AD // Side BC

16. A quadrilateral which has
opposite sides parallel is
called a parallelogram.

17. B
Seg AB = Seg DC , Seg AD = Seg BC.
l( AO) = l(CO) , l(BO) = l(DO)
< A = < C , < B = <D.
D
C
O

18. RECAPITULATION
Sr.
no. Quadrilaterals
Properties of quadrilaterals
1)
1) The diagonals of a square are congruent.
2) The diagonals of a square bisect each other.
3) Each diagonal of a square is the perpendicular
Square bisector of the other.
2)
Rectangle
1) The opposite sides of a rectangle are congruent.
2) The diagonals of a rectangle are congruent.
3) The diagonals of a rectangle bisect each other.

19. Sr.
no. Quadrilaterals
CONTD…
Properties of quadrilaterals
3)
1) The diagonals of a rhombus bisect each other.
2) Each diagonal of a rhombus is the perpendicular
bisector of the other.
3) The opposite angles of a rhombus are equal.
4)
1) The opposite sides of a parallelogram are congruent.
2) The opposite angles of a parallelogram are congruent.
3) The diagonals of a parallelogram bisect each other.
Parallelogram

20. evaluation
A) Define quadrilaterals?
B) State the properties of a rectangle?
C) State the properties of a rhombus?
D) Look at the figure of the rhombus and answer the following
questions
A
B C
D
O
1) Length of side AD = 4cm. Then what are the
Lengths of sides AB, BC, CD ?
2) m<AOD = ?
3) IF l(BO) =2.5 , THEN l(BD) = ?