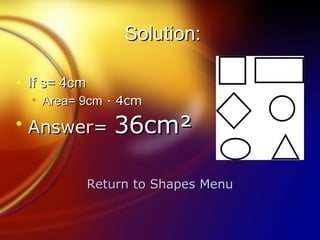
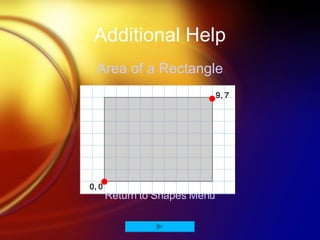
The document is about Pythagoras and the Pythagorean theorem. It provides biographical information on Pythagoras, the history and origins of the theorem, references to the theorem in popular culture, an interactive tool for proving the theorem, and applications of the theorem. It also includes sections on shapes and geometry that define shapes like circles, triangles, squares and rectangles and provide formulas for calculating their areas.

1. Geometry and Measurement Brad Fewins Stephen Hummel

2. Table of Contents: Pythagorean Theorem Pythagoras of Samos History More on History Pythagoras Quotes References to the Pythagorean Theorem More References Proving the Theorem Real-World Application Works Cited

3. Table of Contents: Shapes Circle Triangle Square Rectangle Rhombus Additional Help Works Cited

4. Pythagoras of Samos Pythagoras was an extremely important mathematician in history. He is called the first pure mathematician by many. Unfortunately, we know relatively little about his mathematical achievements. Return to Pythagoras Menu

5. History There is a lot of debate whether the theorem was discovered once or many times. Many believe that the theorem was known to the Babylonians 1000 years previous to Pythagoras but he may have been the first to prove it. Return to Pythagoras Menu

6. More on history Pythagoras , whose dates are commonly given as 569–475 BC, used algebraic methods to construct Pythagorean triples. There is a legend that Pythagoras sacrificed 100 oxen in light of the discovery. Return to Pythagoras Menu

7. Pythagoras Quotes Number is the ruler of forms and ideas, and the cause of gods and demons. Every man has been made by God in order to acquire knowledge and contemplate. Geometry is knowledge of the eternally existent. Number is the within of all things. There is geometry in the humming of the strings. Time is the soul of this world. Return to Pythagoras Menu

8. References to the Pythagorean Theorem ~In the Wizard of Oz when the scarecrow gets his diploma from the wizard he immediately shows off his knowledge by exclaiming an incorrect version of the formula, "The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side. Oh, joy, oh, rapture. I've got a brain!" ~In an episode of the Simpson's, Homer quotes the scarecrow’s version of the theorem A man nearby then yells out, "That's a right triangle, you idiot!" (although that still doesn’t completely correct the scarecrows version) Return to Pythagoras Menu

9. More References ~The speech software on the MacBook also references the previous incorrect statement of the theorem. It is a sample speech, Ralph is the voice setting. ~Also, Uganda released a coin with the shape of a right triangle inscribed on it. The coin has a picture of Pythagoras and the Pythagorean theorem on it. Return to Pythagoras Menu

10. Proving the Theorem This website includes an interactive java applet that allows the audience to follow along well enough to understand the geometry involved. http://www.sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Pythagoras/pythagoras.html Return to Pythagoras Menu

11. Return to Pythagoras Menu

12. The answer to this real world application a=90 Since the distance b=90 between home plate c^2=a^2+b^2 and second base is c^2=90^2+90^2 the same as the c^2=8100+8100 distance between c^2=16200 first base and third c= base, the answer for c=127.279 both distances will be Back to the problem the same. Click Image to Return to Pythagoras Menu

13. Circle Area of a Circle: A= ∏(3.14)·r² Or ∏∙r∙r Example: R= 3 inches, what is the area? ∏∙ 3 inches·3 inches = 28.26in² Return to Shapes Menu

14. Triangle Area= ½· base · height Base=12cm Height=9cm ½·12·9= Click image to reveal answer!

15. Answer: A= ½·108 in²= A=54 inches² Return to Shapes Menu

16. Square Area= width · height X= 6 meters, what is the area? 6m·6m= 36m² Return to Shapes Menu

17. Rectangle Area= Width · Height If s=4, what is the Area? Click image for answer

18. Solution: If s= 4cm Area= 9cm · 4cm Answer= 36cm² Return to Shapes Menu

19. Rhombus Area for base times height method: Click image for solution! Area= base · altitude or height Example: If base= 129cm Height= 34cm Area= ?

20. Answer: Rhombus Area= 129cm · 34cm= 4386 cm² Return to Shapes Menu Return to Pythagoras Menu

21. Additional Help Area of a Circle Return to Shapes Menu

22. Additional Help Area of a Rectangle Return to Shapes Menu

23. Works cited http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Pythagoras.html http:// en.wikipedia.org/wiki/Pythagorean_theorem http://www.geom.uiuc.edu/~demo5337/Group3/hist.html http://www.sunsite.ubc.ca/LivingMathematics/V001N01/UBCExamples/Pythagoras/pythagoras.html http:// www.youtube.com/watch?v =1ZReTq9V2RI http:// www.youtube.com/watch?v = ECJfSyg_Obo Return to Pythagoras Menu Return to Shapes Menu