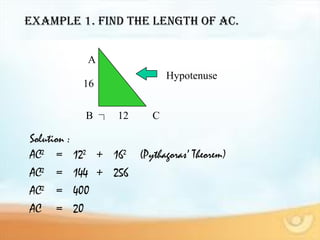
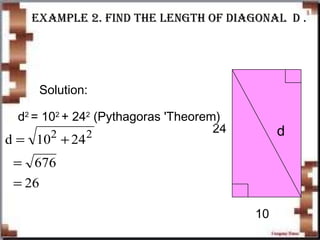
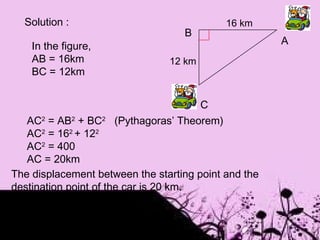
This presentation discusses the Golden Ratio and Pythagorean Theorem through three main points: 1) It provides an overview of the Pythagorean Theorem, which states that in any right triangle, the square of the hypotenuse is equal to the sum of the squares of the two legs. 2) It presents an animated proof of the Pythagorean Theorem using squares and translations. 3) It gives examples and applications of using the Pythagorean Theorem to solve problems involving right triangles, such as finding missing side lengths or distances.

1. A PRESNTATION ON
GOLDEN RATIO

2. Michael Mastlin

6. A LITTLE MORE
In any right triangle, the square of the length of the
hypotenuse is equal to the sum of the squares of the
lengths of the legs."
This relationship can be stated as:
and is known as the
Pythagorean Theorem
a, b are legs.
c is the hypotenuse

7. Starting with a right triangle and squares on each side, the middle size square is
cut into congruent quadrilaterals .Then the quadrilaterals are hinged and rotated
and shifted to the big square. Finally the smallest square is translated to cover the
remaining middle part of the biggest square. A perfect fit! Thus the sum of the
squares on the smaller two sides equals the square on the biggest side.
Afterward, the small square is translated back and the four quadrilaterals are directly
translated back to their original position.
Animated Proof of the Pythagorean Theorem

8. ANIMATED PROOF OF THE PYTHAGOREAN THEOREM

9. iven:- ABC is a right angle Triangle.
angle B =900
T.P:- AC2
= AB2
+BC2
Construction:- To draw BD ⊥ AC .
A
B C
D
Proof:- In ADB and ABC
Angle A = Angle A (common)
Angle ADB = Angle ABC (each 900
)
ADB ~ ABC ( A.A corollary )
So that AD/AB = AB/AC
AB2
= AD X AC _________(1)
Similarly BC2
= DCXAC _________(2)
Adding (1) & (2) , we get
AB2
+BC2
= AD X AC + DCXAC
= AC (AD +DC)
= AC . AC
=AC2
Therefore
AB2
+BC2
=AC2
PYTHAGOREAN THEOREM IN TEXT BOOK OF 10TH
CLASS

10. Typical
ExamplEs

11. ExamplE 1. Find thE lEngth oF aC.
Hypotenuse
AC2
= 122
+ 162
(Pythagoras’ Theorem)
AC2
= 144 + 256
AC2
= 400
AC = 20
A
CB
16
12
Solution :

12. ExamplE 2. Find thE lEngth oF diagonal d .
10
24 d
Solution:
d2
= 102
+ 242
(Pythagoras 'Theorem)
d = +
=
=
10 24
26
2 2
676

13. 16km
12km
1.A car travels 16 km from east to west. Then
it turns left and travels a further 12 km. Find
the displacement between the starting point
and the destination point of the car.
N
?
Application of Pythagoras’ Theorem

14. 16 km
12 km
A
B
C
Solution :
In the figure,
AB = 16km
BC = 12km
AC2
= AB2
+ BC2
(Pythagoras’ Theorem)
AC2
= 162
+ 122
AC2
= 400
AC = 20km
The displacement between the starting point and the
destination point of the car is 20 km.

15. Q.) The height of a tree is 5 m. The
distance between the top of it and the tip
of its shadow is 13 m. Find the length of
the shadow L.
Solution:
132
= 52
+ L2
(Pythagoras’ Theorem)
L2
= 132
- 52
L2
= 144
L = 12
5 m
13 m
L

17. All efforts by yash agarwal