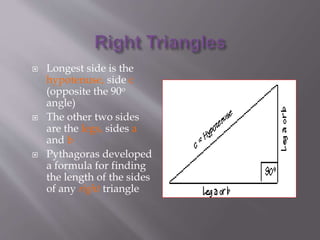
Pythagoras, an ancient Greek mathematician, is traditionally credited with discovering the Pythagorean theorem around 570 BC. The theorem states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. It has numerous proofs and can be generalized beyond right triangles. The Pythagorean theorem is fundamental in areas like navigation, land surveying, and ramp design and has attracted interest outside mathematics for its symbolic power.

1. Maths Assignment

2.  Lived in Greek during
the sixth century B.C.
 Considered the first true
mathematician
 Used mathematics as a
means to understand the
natural world
 First to teach that the
earth was a sphere that
revolves around the sun
 Made a very important
theorem for Right
triangles

3. The Pythagorean theorem is named after
the Greek mathematician Pythagoras (ca. 570 BC—ca. 495 BC), who
by tradition is credited with its discovery and proof,[2][3] although it
is often argued that knowledge of the theorem predates him. There
is evidence that Babylonian mathematiciansunderstood he
formula, although there is little surviving evidence that they used
it in a mathematical framework.[4][5]
The theorem has numerous proofs, possibly the most of any
mathematical theorem. These are very diverse, including both
geometric proofs and algebraic proofs, with some dating back
thousands of years. The theorem can be generalized in various
ways, including higher-dimensional spaces, to spaces that are not
Euclidean, to objects that are not right triangles, and indeed, to
objects that are not triangles at all, but n-dimensional solids. The
Pythagorean theorem has attracted interest outside mathematics as
a symbol of mathematical abstruseness, mystique, or intellectual
power; popular references in literature, plays, musicals, songs,
stamps and cartoons abound.

4.  Longest side is the
hypotenuse, side c
(opposite the 90o
angle)
 The other two sides
are the legs, sides a
and b
 Pythagoras developed
a formula for finding
the length of the sides
of any right triangle

5. “For any right
triangle, the sum of
the areas of the two
small squares is
equal to the area of
the larger.”
a2 + b2 = c2

6. (3,4,5) (5,12,13) (7,24,25) (8,15,17) (9,40,41)
(11,60,61) (12,35,37) (13,84,85) (16,63,65)

7.  The Pythagorean theorem has far-reaching ramifications in
other fields (such as the arts), as well as practical applications.
 The theorem is invaluable when computing distances between
two points, such as in navigation and land surveying.
 Another important application is in the design of ramps. Ramp
designs for handicap-accessible sites and for skateboard parks
are very much in demand.

8. From this Slide I was able to learn:-
 Identify the sides of right angle as legs and
hypotenuse
 Explain and prove the pytha goras Theorem
 Apply this theorem to find the lengths of
right triangles
 Pythagorean Triplets

9. • Ramifications- a complex or
unwelcome consequence of an action
or event.

10. Great info on the Pythagorean theorem,
Pythagoras, and other math-related topics:
 Pythagoras of Samos
 Microsoft Encarta 2000
 Wikipedia

11. THANK YOU