This document presents information about Pythagoras and his famous theorem. It discusses that Pythagoras was a Greek philosopher from Samos in the 6th century BC who made important contributions to mathematics and philosophy. It provides two proofs of Pythagoras' theorem - that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. The document also includes animations demonstrating proofs of the theorem through manipulating squares built on the sides of right triangles.

1. PROJECT ON :
PYTHAGORAS THEOREM
PRESENTED BY GROUP 5
CREATED BY SOURAV NETI
SUBJECT TEACHER – D.K. BHUI Sir

2. GROUP MEMBERS :
SWATI SAGARIKA ROUT ( L )
MITALI GOUDA
SOURAV NETI ( A.L. )
SATYA PRAKASH RAY
RAKESH KUMAR BEHERA
ABHIJEET LENKA

3. Pythagoras (~580-500 B.C.)
He was a Greek philosopher responsible for important developments in
mathematics, astronomy and the theory of music.

4. Pythagoras of Samos was an lonian Greek
philosopher, mathematician , and has been credited as
the founder of the movement called Pythagoreanism .
Most of the information about Pythagoras was written
down centuries after he lived , so very little reliable
information is known about him . He was born on the
island of Samos and travelled visiting Egypt and
Greece and maybe India and in 520 BC returned to
Samos . Around 530 BC he moved to Croton in
Magna Graecia , and there established some kind of
school or guild .

5. Pythagoras made influential contributions to
philosophy and religion in the late 6th century BC . He
is also reversed as a great mathematician and scientist
and is best known for Pythagoras theorem which bears
his name . However , because legend and obfuscation
cloud his work even more than that of the other pre-
Socratic philosophers , one can give only a tentative
account of his teachings , and some have questioned
whether he contributed much to mathematics or natural
philosophy . Many of the accomplishments credited to
Pythagoras may actually have been accomplishments
of his colleagues and successors .

6. Some accounts mention that the philosophy associated
with Pythagoras was related to mathematics and that
numbers were important . It was said that he was the
first man to call himself as philosopher , or lover of
wisdom , and Pythagorean ideas exercised a marked
influence on Plato , and through him , all of western
philosophy .
SCULPTOR OF
PYTHAGORAS

7. STATEMENT
In a right triangle the square of hypotenuse is equal to the
sum of the square of other two sides .
MATERIALS REQUIRED
1. Colour paper
2. Pair of scissors
3.Glue
4. Geometry Box

8. PROCEDURE
1) LET US DRAW A TRIANGLE ABC OF SIDES OF
3CM , 4CM AND 5CM RESPECTIVELY .
2)TAKE OR DRAW ANOTHER TRIANGLE OF
SAME MEASUREMENT AND DRAW OR CUT
SQUARES OF SIDES 3CM , 4CM AND 5CM AND
PASTE THEM ON SIDES OF TRIANGLE .
3)TAKE ANOTHER TWO SQUARES OF SIDES
3CM , 4CM AND 5CM AND PASTE FOUR
TRIANGLES ACCORDING .
4)TAKE ANOTHER SQUARE OF SIDE 5 CM AND
PASTE YOUR PIECES OF THE TRIANGLE , SO
THAT THIS FORM A SQUARE OF SIDE (A+B) .

9. 1. cut a triangle
with base 4 cm
and height 3
cm
0 1 2 3 4 5
4 cm
012345
3cm
2. measure the
length of the
hypotenuse .
Here we have the first figure :
A
B C
a
b
c
FIG 1

10. a
a
a
a
b
b
b
b
b
a c
c
c
c
c
FIG 2

11. Consider a square PQRS with sides a + b
a
a
a
a
b
b
b
b
c
c
c
c
4 congruNow, the square is cut into
- 4 congruent right-angled
triangles and
- n- 1 smaller square with sides c
- 1 smaller square with sides c .
P Q
R S
FIG 3

12. a + b
a + b
A B
CD
FIG 4

13. a + b
a + b
A B
CD
Area of square ABCD
= (a + b) 2
b
b
a b
b
a
a
a
c
c
c
c
P Q
RS
Area of square PQRS
= 4 + c
2ab
2






a 2 + 2ab + b 2 = 2ab + c 2
a2
+ b2
= c2
FIG 5

14. Theorem states that:
"The area of the square built upon the hypotenuse of a right triangle is
equal to the sum of the areas of the squares upon the remaining sides."
The Pythagorean Theorem asserts that for a right triangle, the square
of the hypotenuse is equal to the sum of the squares of the other two
sides: a2 + b2 = c2
The figure above at the right is a visual display of the theorem's
conclusion. The figure at the left contains a proof of the theorem,
because the area of the big, outer, green square is equal to the sum of
the areas of the four red triangles and the little, inner white square:
c2 = 4(ab/2) + (a - b)2 = 2ab + (a2 - 2ab + b2) = a2 + b2

15. ANIMATED PROOF OF PYTHAGORAS THEOREM

16. WE HAVE PROVED PYTHAGORAS
THEOREM BUT THERE IS ONE
MORE WAY TO PROVE AND THAT
IS SHOWN FROM THE NEXT
SLIDE .

17. STATEMENT
In a right triangle the square of hypotenuse is equal to the
sum of the square of other two sides .
MATERIALS REQUIRED
1. Colour paper
2. Pair of scissors
3.Glue
4. Geometry Box

18. PROCEDURE
1) Let us draw a triangle ABC of sides of 3cm , 4cm and 5cm
respectively .
2)Take or draw another triangle of same measurement and draw
or cut squares of sides 3cm , 4cm and 5cm and paste them on
sides of triangle .
3)Take another two squares of sides 3cm , 4cm and 5cm and paste
four triangles according .
4)Take another square of side 5 cm and paste your pieces of the
triangle , so that this form a square of side (a+b) .

19. a
a
a
a
b
b
b
b
a
a
a a
b
b
bb
c
c
c
cFIG 6

20. 5) The area of fig.6 and fig.3 are (a+b)^2
respectively . Hence the areas of 5 and 3 are equal
6) Now , we remove four triangles from fig. 5 and 3 .
So the remaining figures must have the same area .
Hence , areas of fig.6 and fig.7 are equal .
b
b
b
b
a
a
a
a
FIG 7
By removing four
triangles from
fig.6 we get
this figure .
Area of square = (side)^2 =
a^2
Similarly,
Area of second square =
(side)^2
=>a^2=a^2+b^2

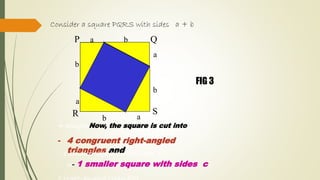
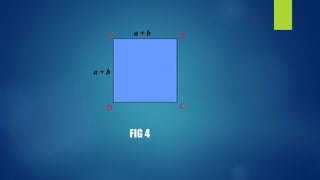
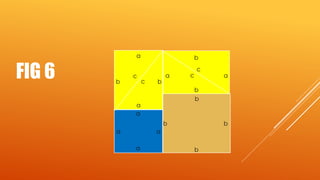
21. By removing four triangles from fig.3 we get the
following figure .
a
a
aaFIG 8
Thus , by comparing fig. 7 and 8 we get that [ a^2 + b ^2 ] .
HENCE PROVED
a

22. ANIMATION OF PYTHAGORAS THEOREM

23. THANK
YOU