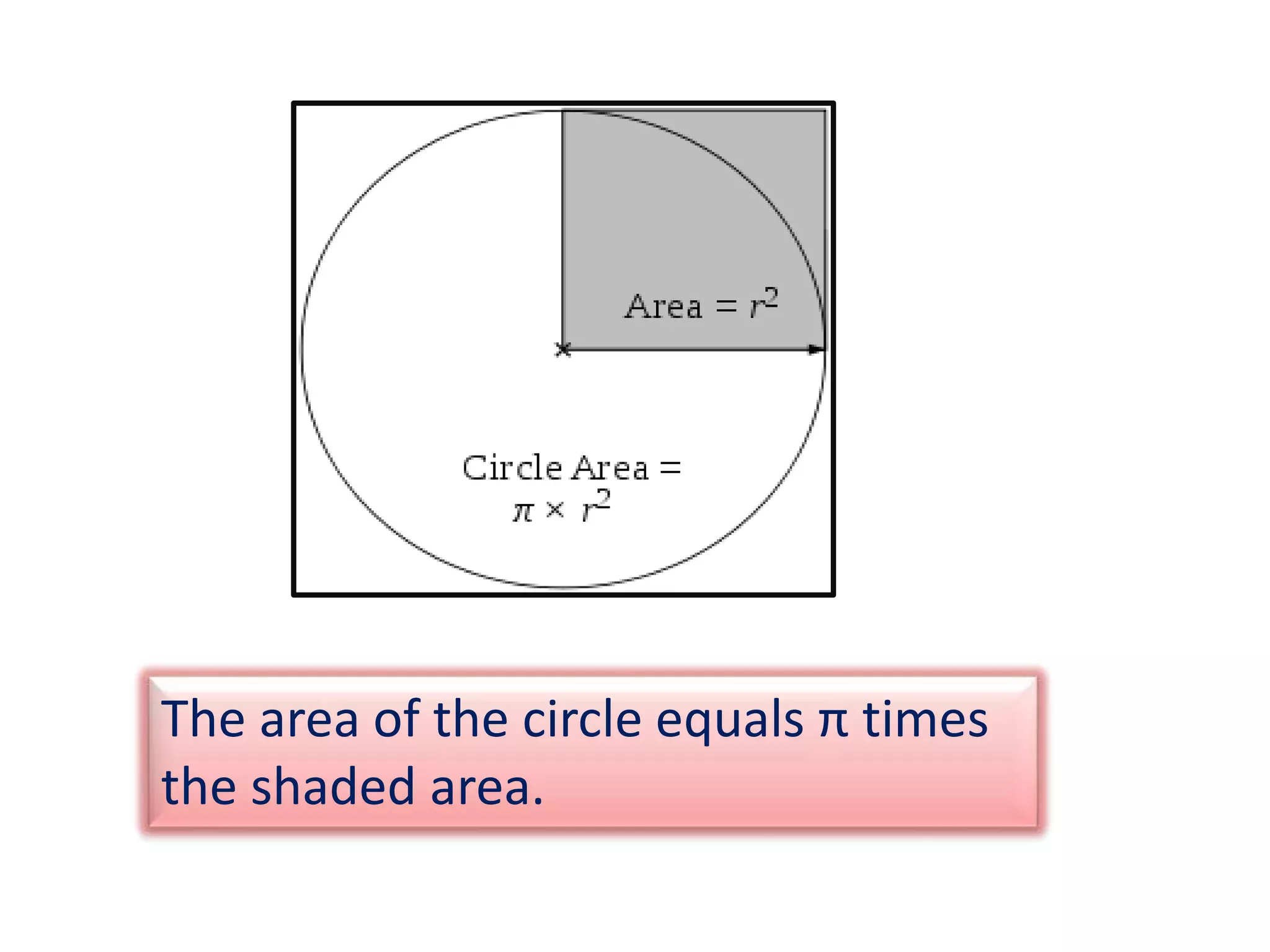
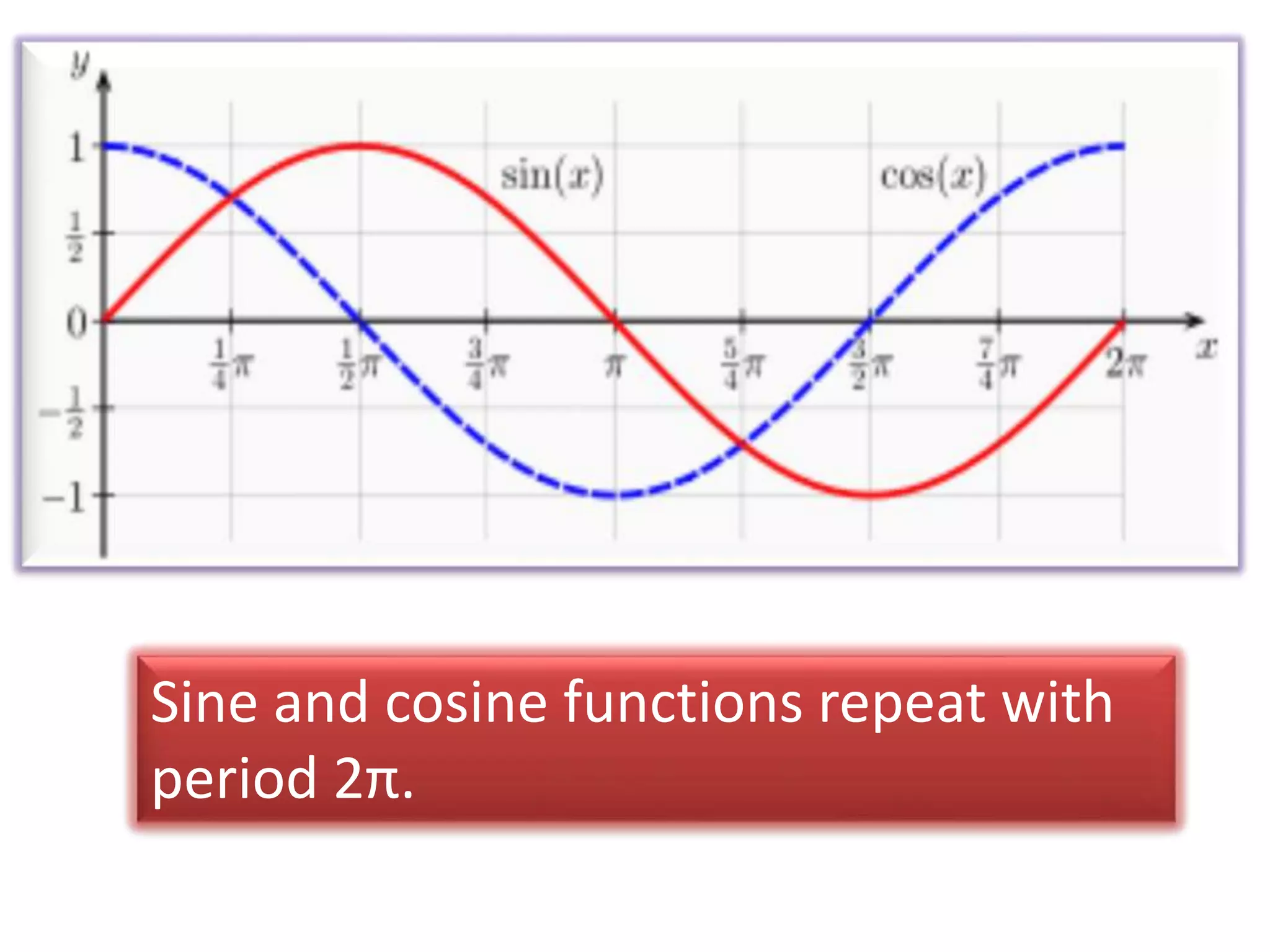
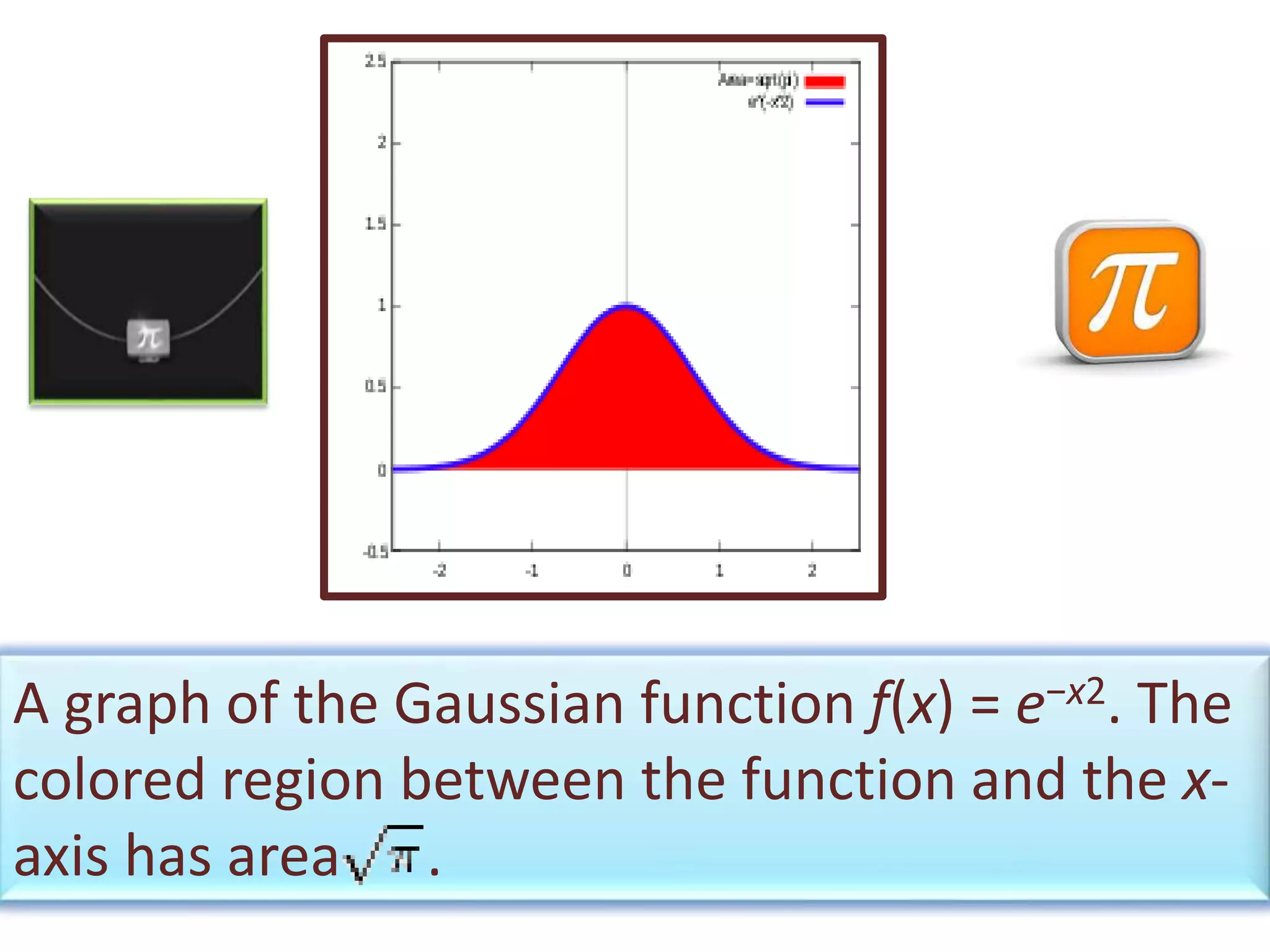
Pi (π) is a mathematical constant representing the ratio of a circle's circumference to its diameter, approximately equal to 3.14159, and is an irrational number that cannot be exactly expressed as a fraction. Popularized by mathematician Leonhard Euler in the 18th century, π is essential in various mathematical and scientific formulas, particularly in geometry, trigonometry, and statistics. Pi Day is celebrated annually on March 14, highlighting its significance in mathematics and culture.

2. • The number pi (symbol: π) is a mathematical
constant that is the ratio of
a circle's circumference to its diameter, and is
approximately equal to 3.14159.
• It has been represented by the Greek letter "π"
since the mid-18th century, though it is also
sometimes written as pi.
• π is an irrational number, which means that it
cannot be expressed exactly as a ratio of
two integers (such as 22/7); consequently,
its decimal representation never ends and
never settle into a permanent repeating pattern.

3. CLICK HERE

4. • π is commonly defined as the ratio of
a circle's circumference C to its diameter d.
• The ratio C/d is constant, regardless of the
circle's size. For example, if a circle has twice
the diameter of another circle it will also have
twice the circumference, preserving the
ratio C/d. This definition of π implicitly makes
use of flat (Euclidean) geometry; although the
notion of a circle can be extended to any

5. curved (non-Euclidean) geometry, these new circles
will no longer satisfy the formula π = C/d. There are
also other definitions of π which do not mention
circles at all, for example: π is twice the smallest
positive x for which cos(x) equals 0.
The circumference of a circle is slightly more
than three times as long as its diameter. The
exact ratio is called π.

6. • After Jones introduced the Greek letter in 1706, it
was not adopted by other mathematicians
until Euler started using it, beginning with his 1736
work Mechanica. Before then, mathematicians
sometimes used letters as c or p instead. Because
Euler corresponded heavily with other
mathematicians in Europe, the use of the Greek
letter spread rapidly.

7. In 1748, Euler used π in his widely read
work Introductio in analysin infinitorum (he wrote:
"for the sake of brevity we will write this number as π;
thus π is equal to half the circumference of a circle of
radius 1") and the practice was universally adopted
thereafter in the Western world.

8. Leonhard Euler popularized the use of the
Greek letter π in works he published in 1736
and 1748.

9. •Because π is closely related to the circle, it is
found in many formulae from the fields of
geometry and trigonometry, particularly those
concerning circles, spheres, or ellipses.
•Formulae from other branches of science also
include π in some of their important formulae,
including sciences such as statistics, fractals,
thermodynamics, mechanics, cosmology,
number theory, and electromagnetism.

11. π appears in formulae for areas and volumes of
geometrical shapes based on circles, such
as ellipses, spheres, cones, and torus. Some of the
more common formulae that involve π:
• The circumference of a circle with radius r is 2πr.
• The area of a circle with radius r is
• The volume of a sphere with radius r is 4/3πr3
• The surface area of a sphere with radius r is 4πr2

12. The area of the circle equals π times
the shaded area.

13. • The trigonometric functions rely on angles,
and mathematicians generally use radians as
units of measurement. π plays an important
role in angles measured in radians, which are
defined so that a complete circle spans an
angle of 2π radians.The angle measure of
180° is equal to π radians, and 1° = π/180
radians.
• Common trigonometric functions have
periods that are multiples of π; for example,
sine and cosine have period 2π.

14. Sine and cosine functions repeat with
period 2π.

15. The fields of probability and statistics frequently use
the normal distribution as a simple model for
complex phenomena; for example, scientists
generally assume that the observational error in
most experiments follows a normal distribution. π is
found in the Gaussian function (which is the
probability density function of the normal
distribution) with mean μ and standard deviation σ.

16. A graph of the Gaussian function ƒ(x) = e−x2. The
colored region between the function and the x-
axis has area .

17. π is present in some structural engineering
formulae, such as the buckling formula
derived by Euler, which gives the maximum
axial load F that a long, slender column of
length L, modulus of elasticity E, and area
moment of inertia I can carry without
buckling.

18. The constant π is represented in this
mosaic outside the mathematics
building at the Technische Universität
Berlin.

21. In Popular Culture
Perhaps because of the simplicity of its definition and
its ubiquitous presence in formulae, π has been
represented in popular culture more than other
mathematical constructs.
Palais de la Découverte Pi Day
Importance Given To Pi

22. In the Palais de la Découverte (a science museum in
Paris) there is a circular room known as the "pi
room". On its wall are inscribed 707 digits of π. The
digits are large wooden characters attached to the
dome-like ceiling. The digits were based on an 1853
calculation by English mathematician William
Shanks, which included an error beginning at the
528th digit. The error was detected in 1946 and
corrected in 1949.
Palais de la Découverte

23. Pi Room

24. Pi Day is an annual celebration commemorating
the mathematical constant π (pi). Pi Day is
observed on March 14, since 3, 1, and 4 are
the three most significant digits of π in the
decimal form. In 2009, the United States
House of Representatives supported the
designation of Pi Day. The earliest known
official or large-scale celebration of Pi Day was
organized by Larry Shaw in 1988 at the San
Francisco Exploratorium.
Pi Day

25. Larry Shaw, the organizer of the first Pi Day celebration at
the Exploratorium in San Francisco.

26. Google Doodle
on Pie Day
and Pi Pie at Delft
University

27. EFFORTS BY – ARPAN
GOYAL
SUBMITTED TO - JITENDER
SIR