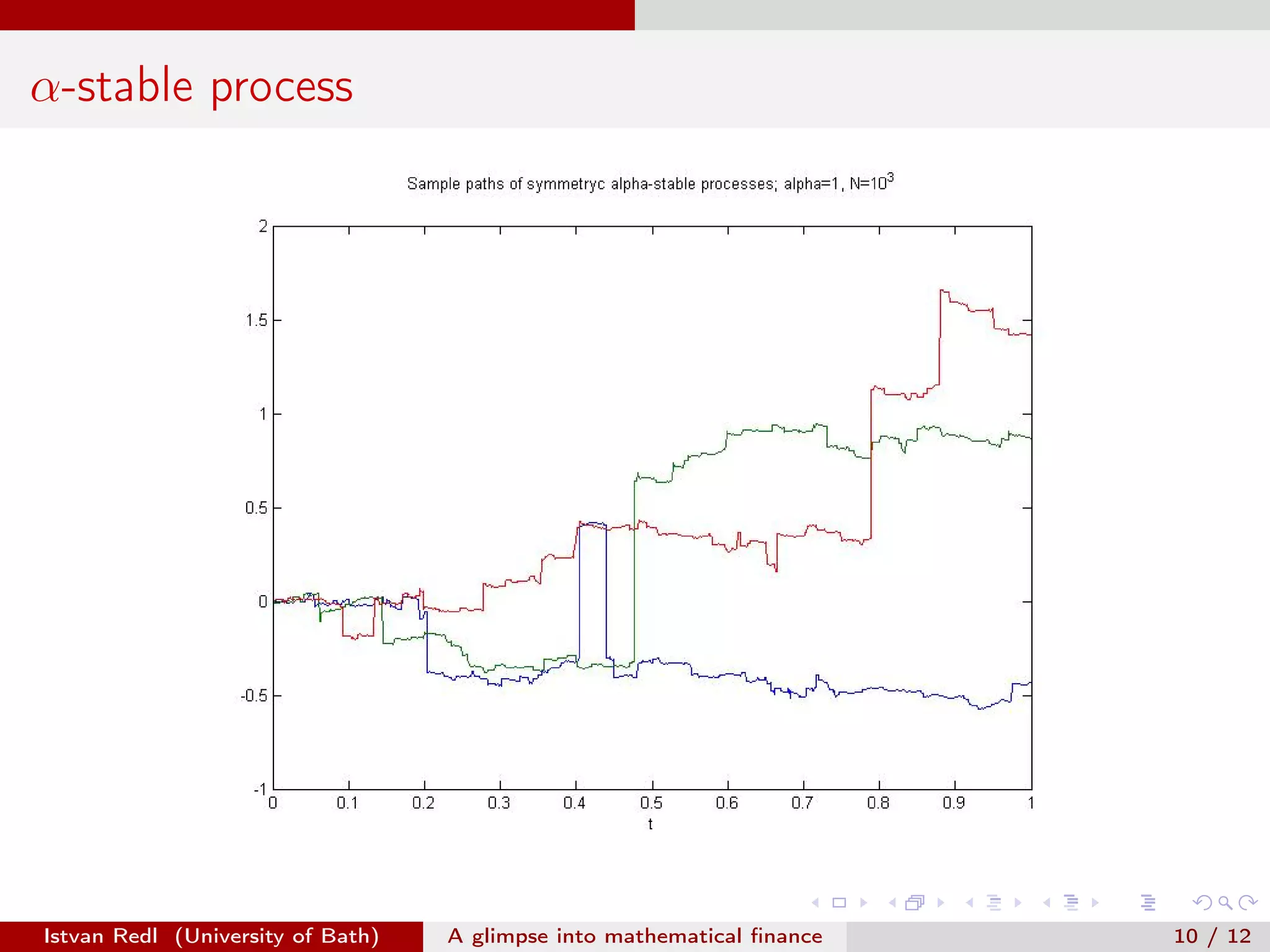
The document presents an overview of mathematical finance with a focus on option pricing models, highlighting its interdisciplinary nature and fundamental theorem of asset pricing (FTAP). It discusses the setup of financial markets, the concept of arbitrage opportunities, and introduces different modeling hierarchies including local and stochastic volatility models. The presentation concludes by inviting questions from the audience.

1. A glimpse into mathematical finance the realm of option pricing models
Istvan Redl
Department of Mathematics
University of Bath
PS Seminar
8 Oct, 2013
Istvan Redl (University of Bath)
A glimpse into mathematical finance
1 / 12

2. Contents
1
Introduction
2
Fundamental Theorem of Asset Pricing (FTAP)
3
Hierarchy of models
Istvan Redl (University of Bath)
A glimpse into mathematical finance
2 / 12

3. Introduction
What is math finance about? - examples
‘Interdisciplinary subject’ ? - problems stem from finance and are treated
with mathematical tools
Math finance traces back to the early ’70s, since then it has become a
widely accepted area within mathematics (Hans Föllmer’s view)
Examples
(i) Optimization - Portfolio/Asset management
(ii) Risk management
(iii) Option pricing
Istvan Redl (University of Bath)
A glimpse into mathematical finance
3 / 12

4. Fundamental Theorem of Asset Pricing (FTAP)
Setup
Consider a financial market, say with d + 1 assets, (e.g. bonds, equities,
commodities, currencies, etc.)
We discuss a simple one-period model, in both periods the assets on the
market have some prices, at t = 0 their prices are denoted by
π = (π 0 , π 1 , . . . , π d ) ∈ Rd+1
¯
+
π is called price system
¯
The t = 1 asset prices are unknown at t = 0. This uncertainty is modeled
by a probability space (Ω, F, P). Asset prices at t = 1 are assumed to be
non-negative measurable functions
¯
S = (S 0 , S 1 , . . . , S d )
Istvan Redl (University of Bath)
A glimpse into mathematical finance
4 / 12

5. Fundamental Theorem of Asset Pricing (FTAP)
Setup cont.
π 0 is the riskless bond, i.e.
π0 = 1
S0 ≡ 1 + r,
with the assumption r ≥ 0.
¯
Consider a portfolio ξ = (ξ 0 , ξ 1 , . . . , ξ d ) ∈ Rd+1 . At time t = 0 the price
of a given portfolio is
d
π·ξ =
¯ ¯
πi ξi
i=0
At time t = 1
d
¯ ¯
ξ · S(ω) =
ξ i S i (ω)
i=0
Istvan Redl (University of Bath)
A glimpse into mathematical finance
5 / 12

6. Fundamental Theorem of Asset Pricing (FTAP)
Arbitrage and martingale measure
Definition (Arbitrage opportunity)
¯
A portfolio ξ ∈ Rd+1 is called arbitrage opportunity if π · ξ ≤ 0, but
¯ ¯
¯ · S ≥ 0 P-a.s. and P(ξ · S > 0) > 0.
¯ ¯
¯
ξ
Definition (Risk neutral measure)
P∗ is called a risk neutral or martingale measure, if
π i = E∗
Si
,
1+r
i = 0, 1, . . . , d .
Theorem (FTAP)
A market model is free of arbitrage if and only if there exists a risk neutral
measure.
Istvan Redl (University of Bath)
A glimpse into mathematical finance
6 / 12

7. Hierarchy of models
Structure of models and associated PDEs
PDEs are typically of type (parabolic)
∂t V + AV − rV = 0
different models lead to different operator A
Black-Scholes: r and σ are constants
dSt = rSt dt + σSt dWt
S0 = s
1
2
(ABS V )(s) = σ 2 s 2 ∂ss V (s) + rs∂s V (s)
2
CEV - constant elasticity of variance: r and σ are constants
dSt = rSt dt + σStρ dWt
S0 = s
0<ρ<1
1
2
(ACEV V )(s) = σ 2 s 2ρ ∂ss V (s) + rs∂s V (s)
2
Istvan Redl (University of Bath)
A glimpse into mathematical finance
7 / 12

8. Hierarchy of models
Structure cont.
Local volatility models: r is a constant, but volatility is a
deterministic function σ : R+ → R+
dSt = rSt dt + σ(St )St dWt
S0 = s
1
2
(ALV V )(s) = s 2 σ 2 (s)∂ss V (s) + rs∂s V (s)
2
Stochastic volatility: r is constant, but volatility is given by another
stochastic process
Yt dWt
S0 = s
dYt = α(m − Yt )dt + β
Yt d W t
dSt = rSt dt +
1 2
1
2
(ASV V )(x, y ) = y ∂xx V (x, y ) + βρy ∂xy V (x, y ) + β 2 y ∂yy V (x, y )
2
2
1
+ r − y ∂x V (x, y ) + α(m − y )∂y V (x, y )
2
Istvan Redl (University of Bath)
A glimpse into mathematical finance
8 / 12

9. Hierarchy of models
Structure cont. - models with jumps
Jump models: r and σ are constants
dSt = rSt dt + σSt dLt
S0 = s
1
2
(AJ V )(s) = σ 2 ∂ss V (s) + γ∂s V (s)
2
(V (s + z) − V (s) − z∂s V (s))ν(dz)
+
R
Istvan Redl (University of Bath)
A glimpse into mathematical finance
9 / 12

10. α-stable process
Istvan Redl (University of Bath)
A glimpse into mathematical finance
10 / 12

11. Thank you for your attention! - Questions
Istvan Redl (University of Bath)
A glimpse into mathematical finance
11 / 12

12. Happy? - Good!
Istvan Redl (University of Bath)
A glimpse into mathematical finance
12 / 12