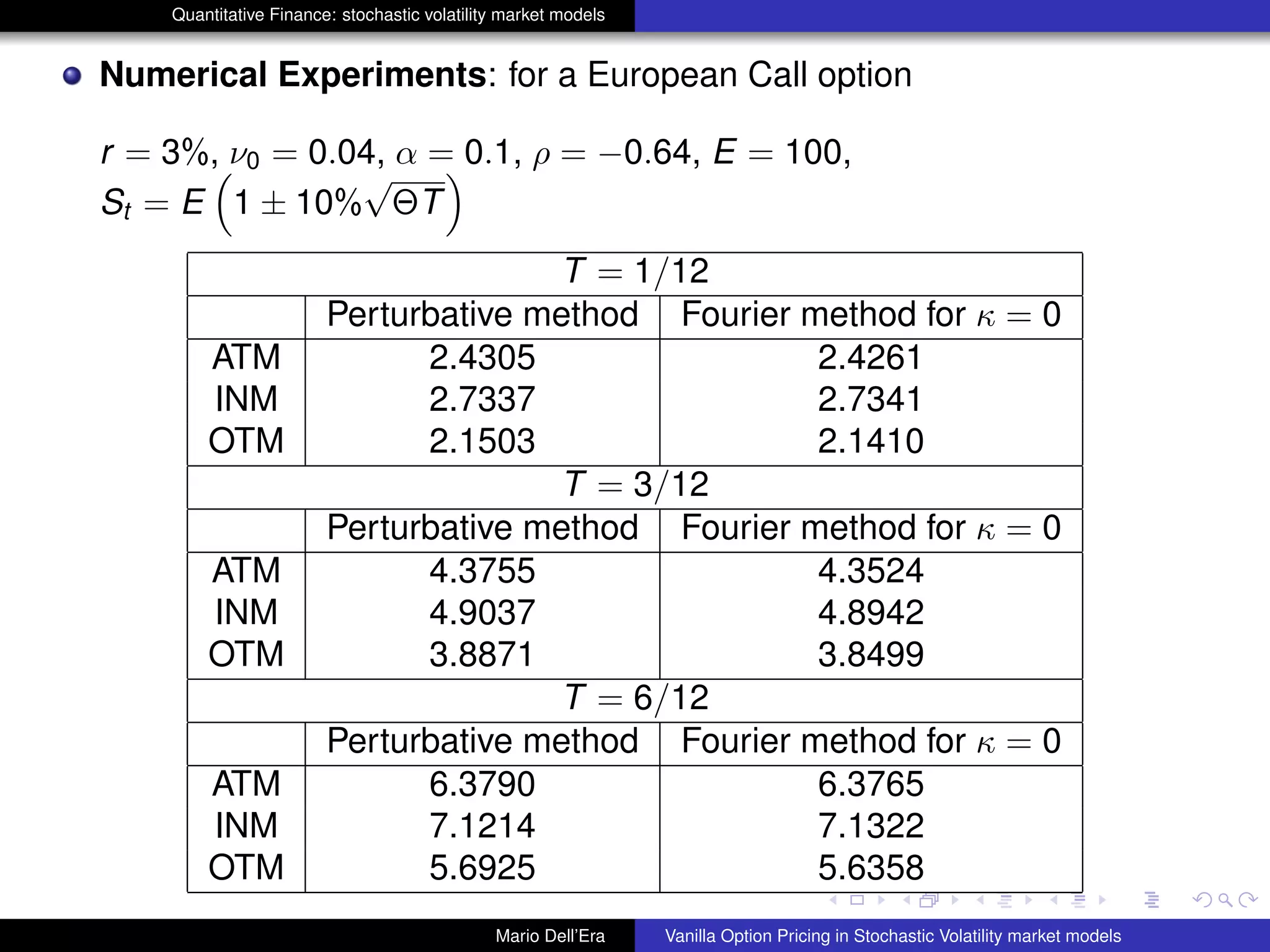
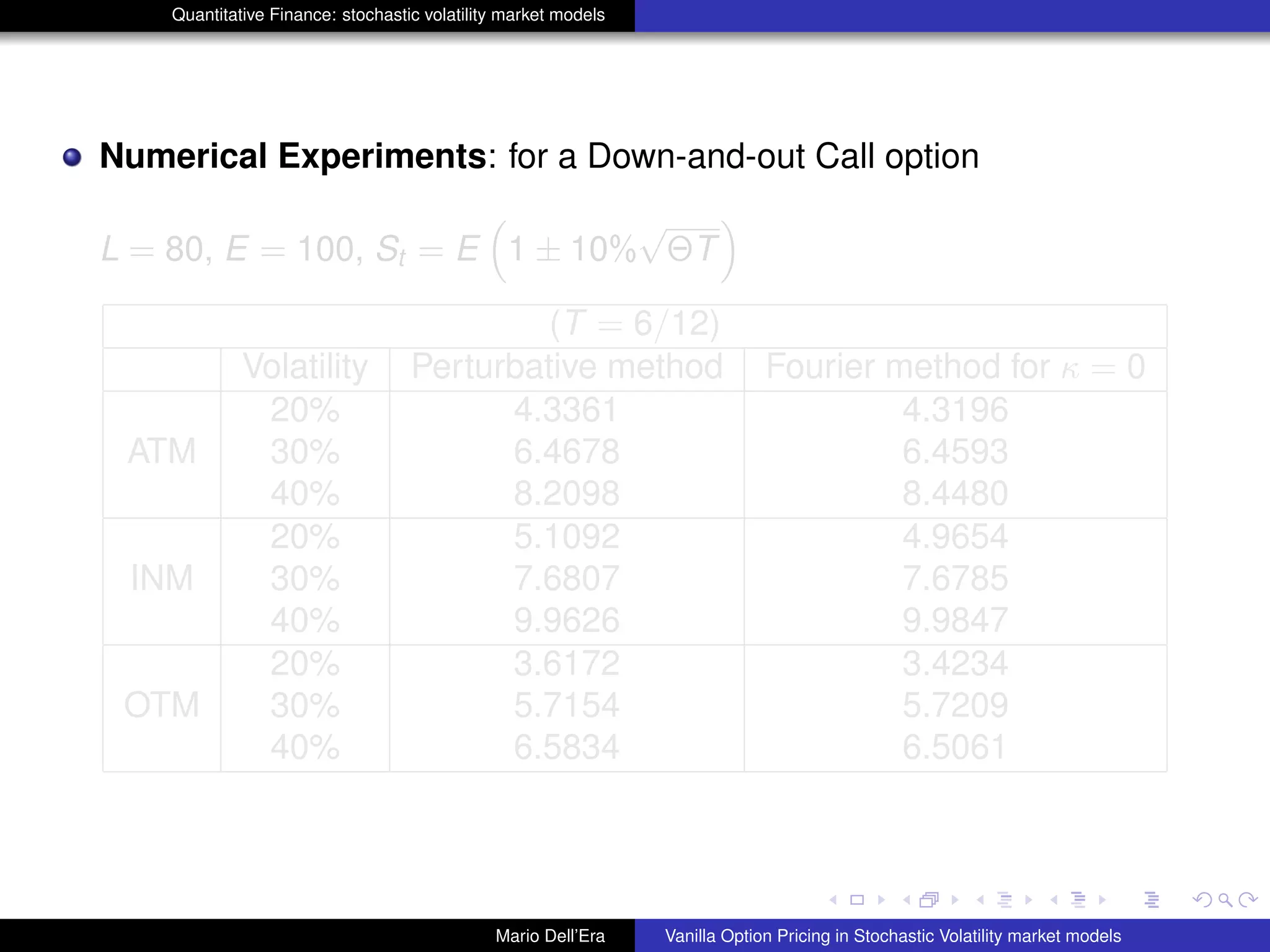
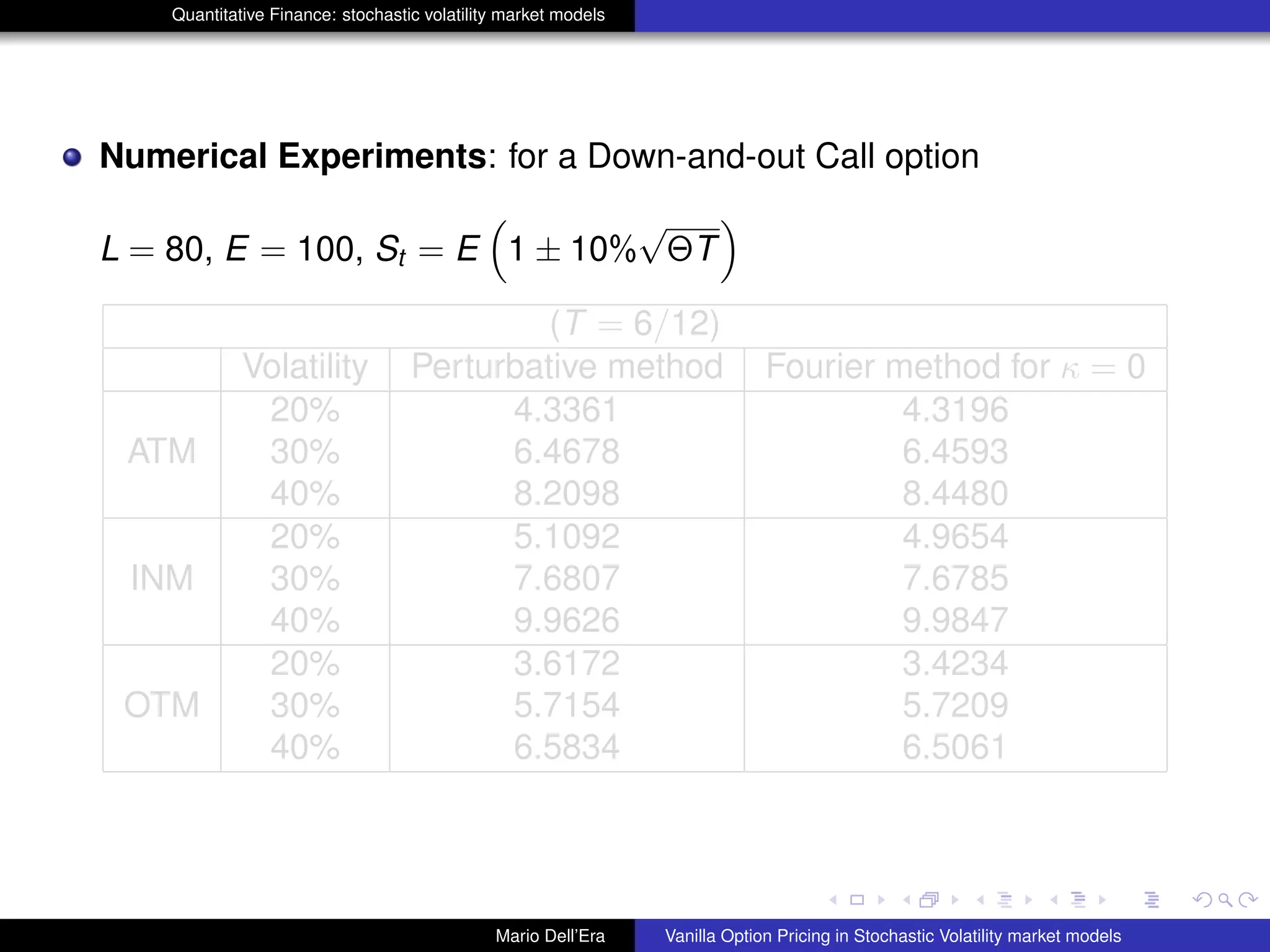
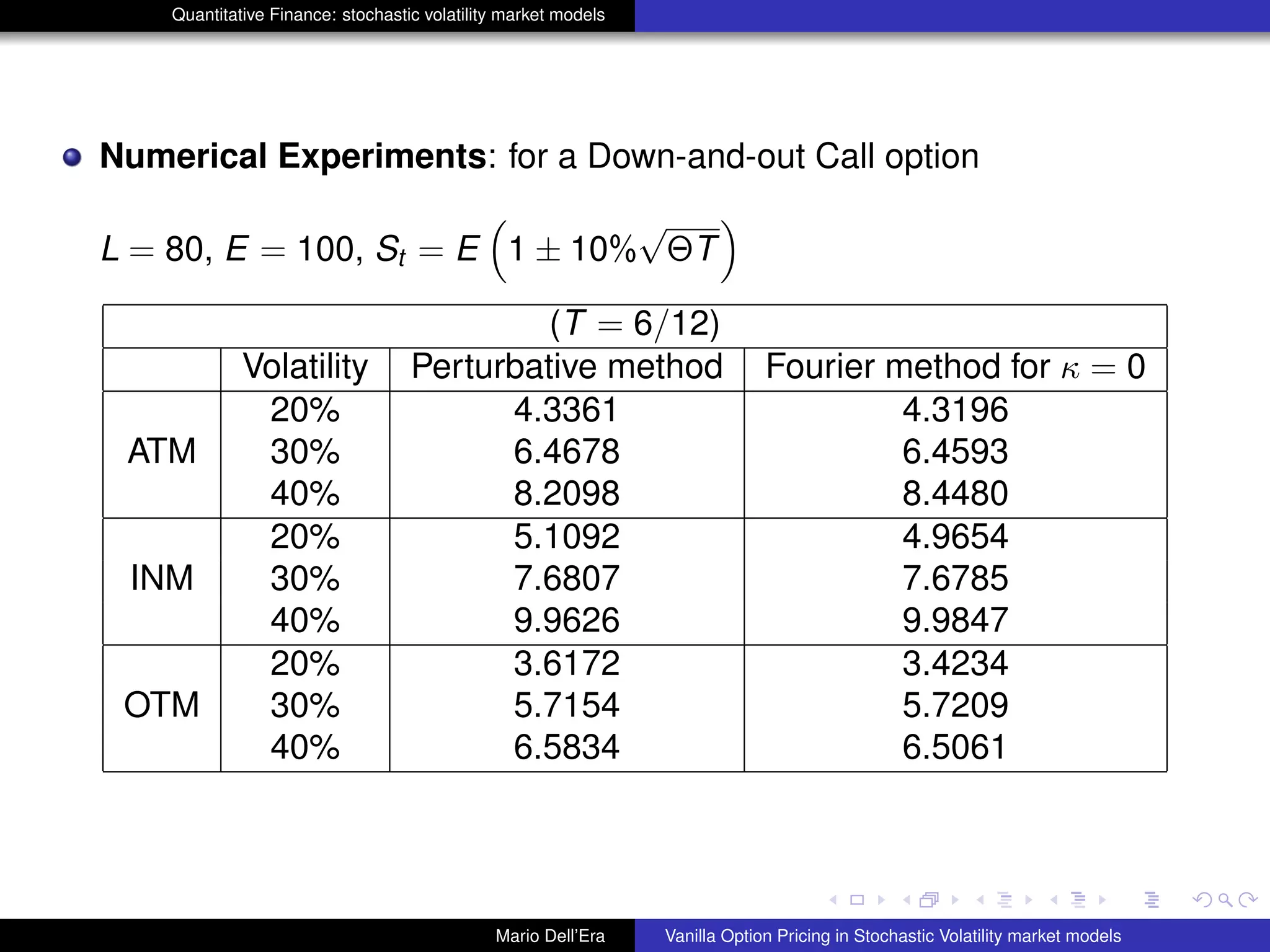
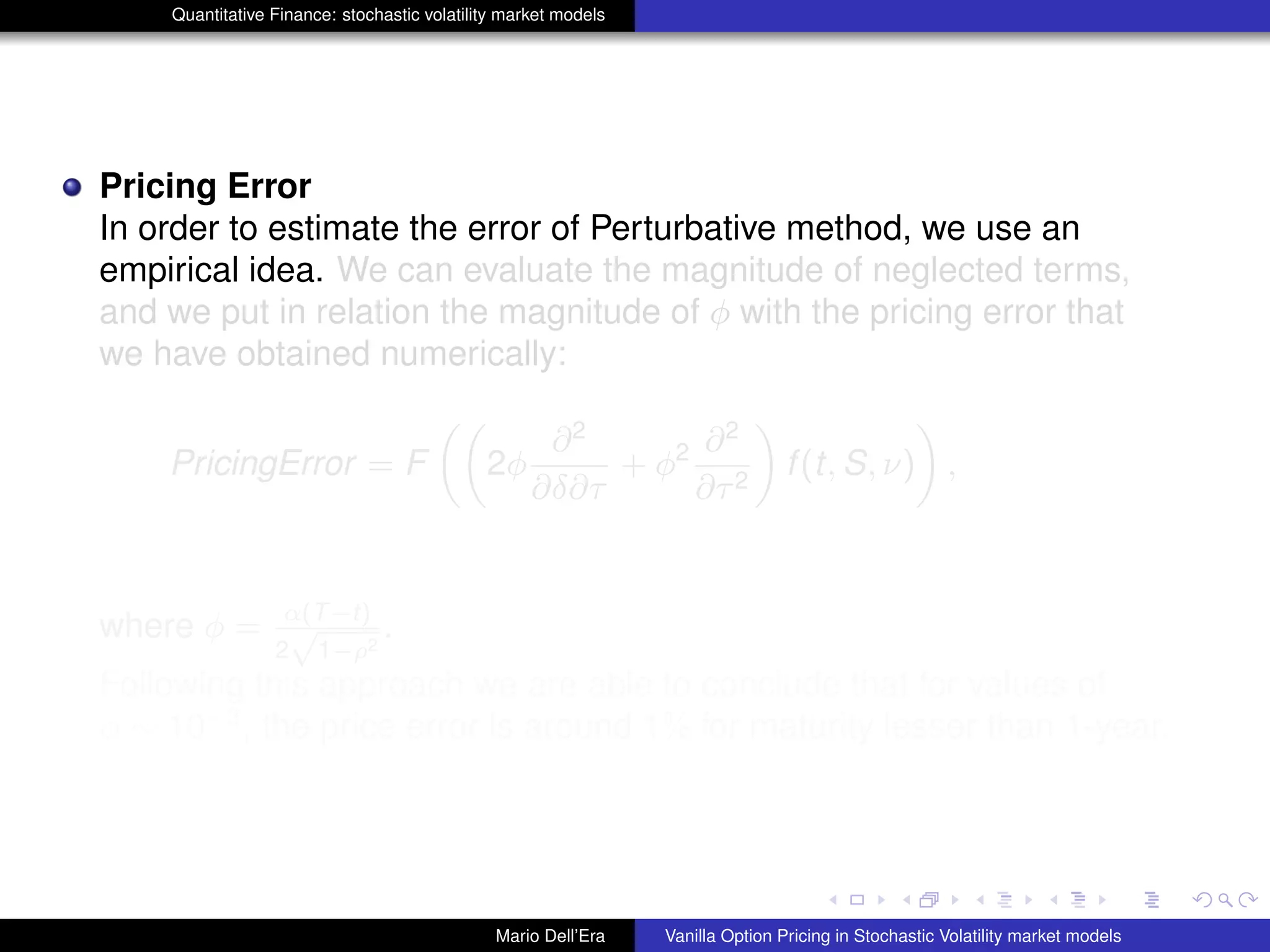
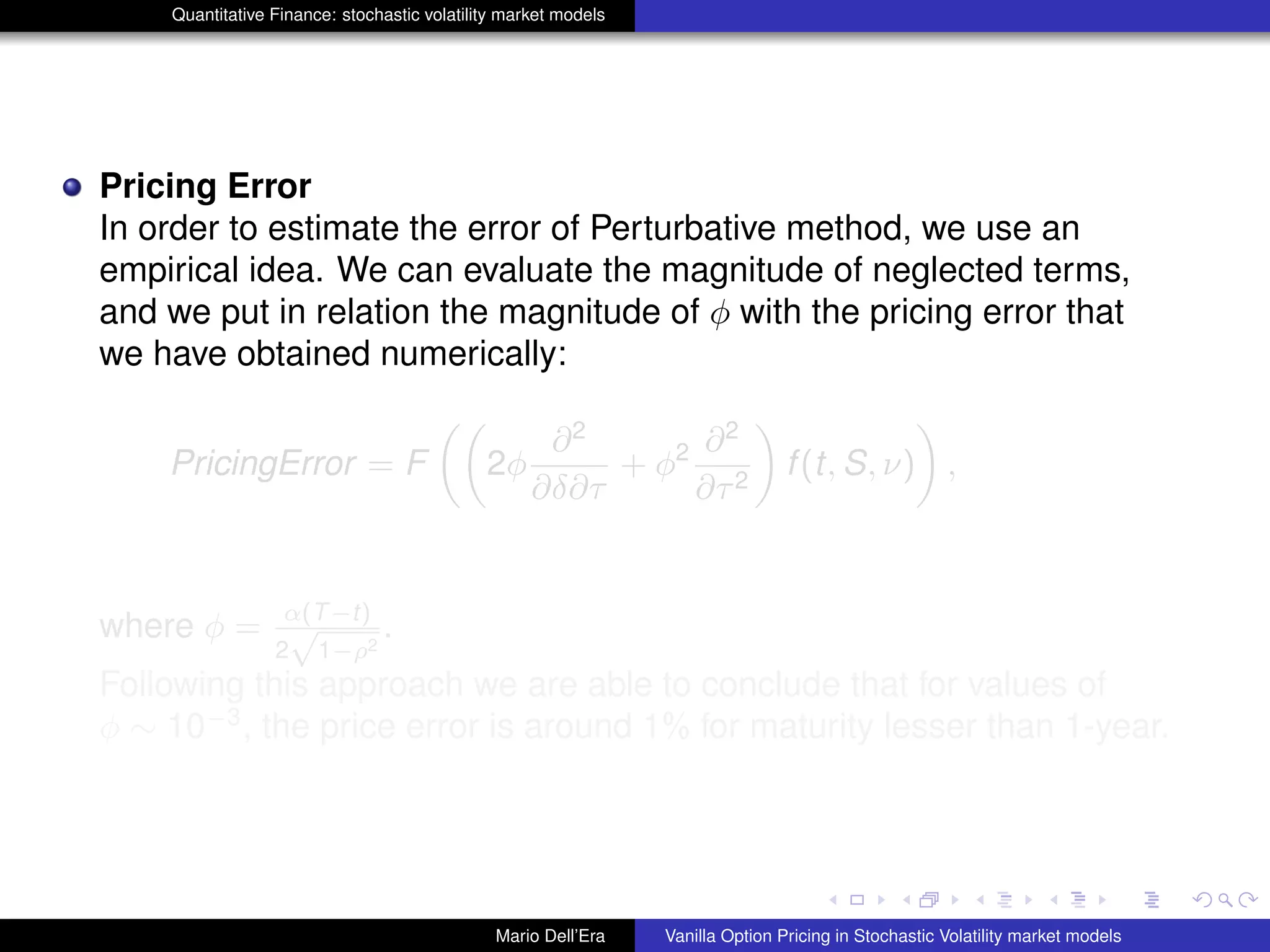
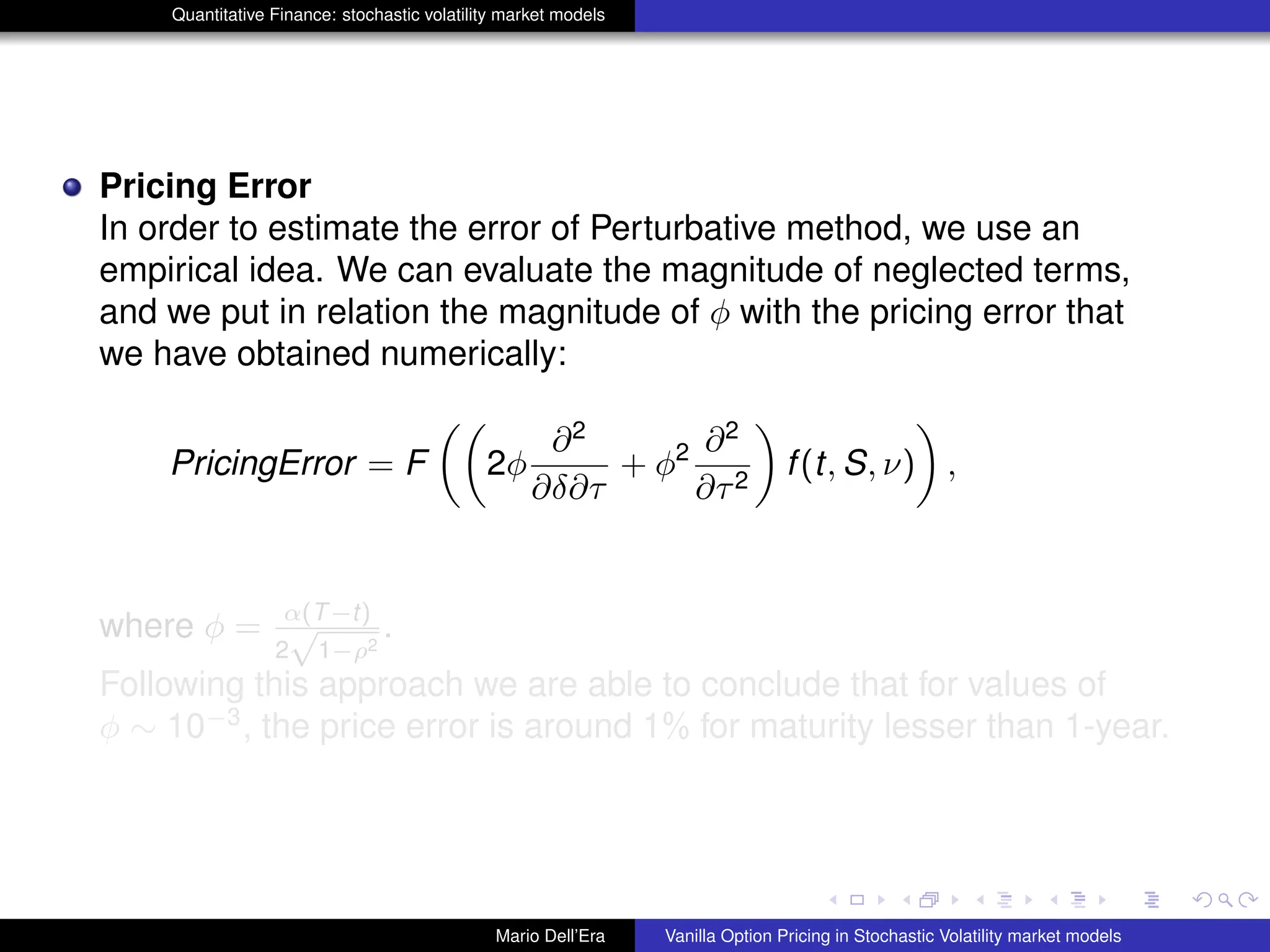
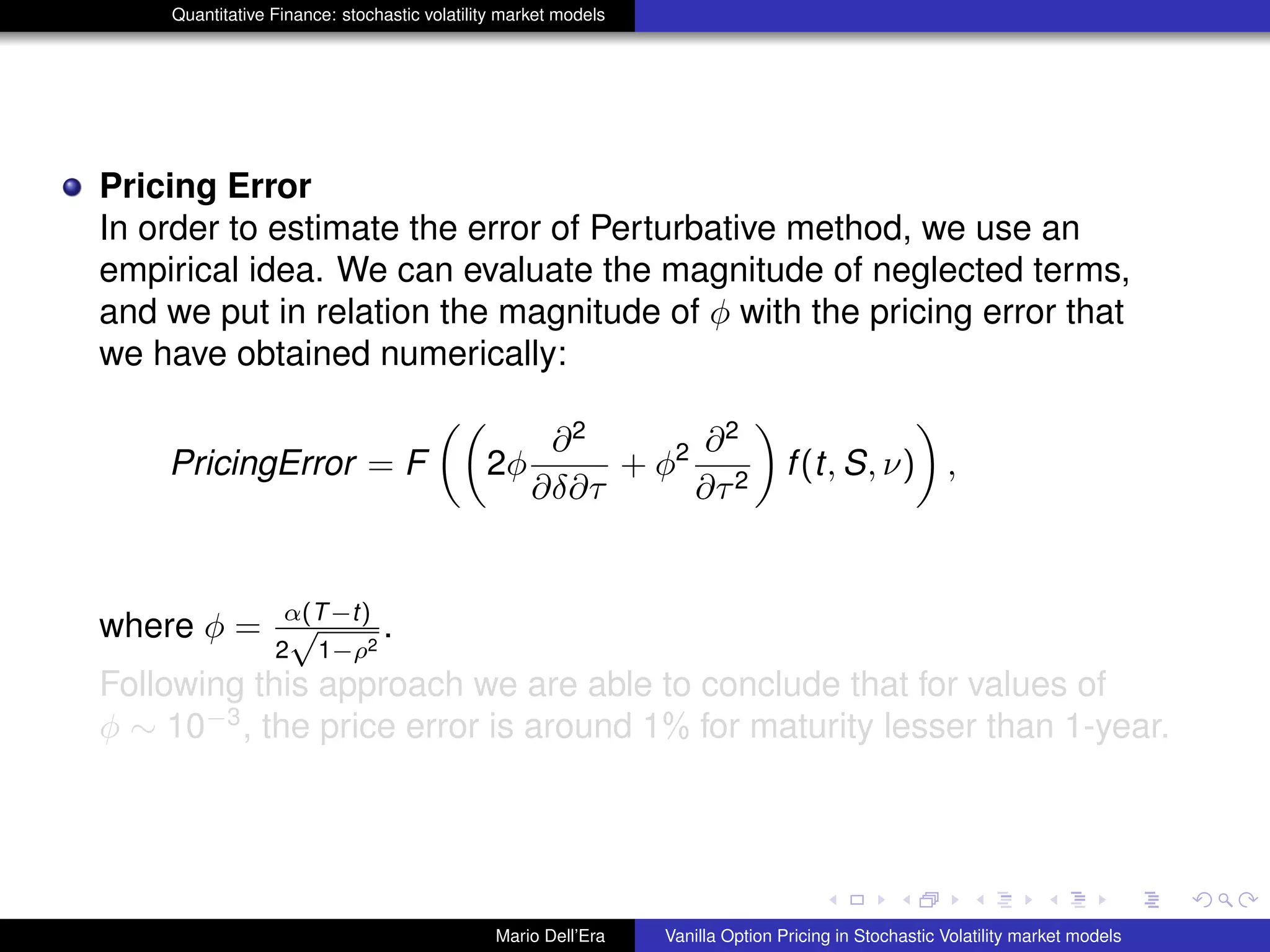
The document discusses pricing vanilla options in stochastic volatility market models. It presents the Heston model equations for the stock price and volatility processes. Applying Ito's lemma yields a PDE for option pricing. Several numerical methods are listed to solve this PDE, including Fourier transforms, finite differences, and Monte Carlo methods. The document also presents an approximation method where some PDE terms are set to zero, yielding simple closed-form pricing formulas for European and barrier options under the Heston model.

1. Quantitative Finance: stochastic volatility market models
Vanilla Option Pricing in Stochastic Volatility
market models
XIII WorkShop of Quantitative Finance
Mario Dell’Era
Scuola Superiore Sant’Anna
January 21, 2013
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

2. Quantitative Finance: stochastic volatility market models
Stochastic Volatility Market Models
dSt = rSt dt + a(σt , St )d ˜W
(1)
t
dσt = b1(σt )dt + b2(σt )d ˜W
(2)
t
dBt = rBt dt
f(T, ST ) = φ(ST )
under a risk-neutral martingale measure Q.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

3. Quantitative Finance: stochastic volatility market models
Heston Model
dSt = rSt dt +
√
νt St d ˜W
(1)
t S ∈ [0, +∞)
dνt = K(Θ − νt )dt + α
√
νt d ˜W
(2)
t ν ∈ (0, +∞)
under a risk-neutral martingale measure Q.
From Itˆo’s lemma we have the following PDE:
∂f
∂t
+
1
2
νS2 ∂2
f
∂S2
+ρναS
∂2
f
∂S∂ν
+
1
2
να2 ∂2
f
∂ν2
+κ(Θ−ν)
∂f
∂ν
+rS
∂f
∂S
−rf = 0
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

4. Quantitative Finance: stochastic volatility market models
Heston Model
dSt = rSt dt +
√
νt St d ˜W
(1)
t S ∈ [0, +∞)
dνt = K(Θ − νt )dt + α
√
νt d ˜W
(2)
t ν ∈ (0, +∞)
under a risk-neutral martingale measure Q.
From Itˆo’s lemma we have the following PDE:
∂f
∂t
+
1
2
νS2 ∂2
f
∂S2
+ρναS
∂2
f
∂S∂ν
+
1
2
να2 ∂2
f
∂ν2
+κ(Θ−ν)
∂f
∂ν
+rS
∂f
∂S
−rf = 0
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

5. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

6. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

7. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

8. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

9. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

10. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

11. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

12. Quantitative Finance: stochastic volatility market models
Numerical methods
(1) Fourier Transform: S.L. Heston (1993)
(2) Finite Difference: T. Kluge (2002)
(3) Monte Carlo: B. Jourdain (2005)
Approximation method
(1) Analytic and Geometric Methods for Heat Kernel: I. Avramidi
(2007)
(2) Implied Volatility: M. Forde, A. Jacquier (2009)
(3) Geometrical Approximation method: M. Dell’Era (2010)
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

13. Quantitative Finance: stochastic volatility market models
Perturbative Method: Heston model with zero drift
In this case we have discussed a particular choice of the volatility
price of risk in the Heston model, namely such that the drift term of
the risk-neutral stochastic volatility process is zero:
dSt = rSt dt +
√
νt St d ˜W
(1)
t ,
dνt = α
√
νt d ˜W
(2)
t , α ∈ R+
d ˜W
(1)
t d ˜W
(2)
t = ρdt, ρ ∈ (−1, +1)
dBt = rBt dt.
f(T, S, ν) = Φ(ST )
under a risk-neutral martingale measure Q.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

14. Quantitative Finance: stochastic volatility market models
Perturbative Method: Heston model with zero drift
In this case we have discussed a particular choice of the volatility
price of risk in the Heston model, namely such that the drift term of
the risk-neutral stochastic volatility process is zero:
dSt = rSt dt +
√
νt St d ˜W
(1)
t ,
dνt = α
√
νt d ˜W
(2)
t , α ∈ R+
d ˜W
(1)
t d ˜W
(2)
t = ρdt, ρ ∈ (−1, +1)
dBt = rBt dt.
f(T, S, ν) = Φ(ST )
under a risk-neutral martingale measure Q.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

15. Quantitative Finance: stochastic volatility market models
From Itˇo’s lemma we have:
∂f
∂t
+
1
2
ν S2 ∂2
f
∂S2
+ 2ραS
∂2
f
∂S∂ν
+ α2 ∂2f
∂ν2
+ rS
∂f
∂S
− rf = 0
After three coordinate transformations we have:
∂f3
∂τ
− (1 − ρ2
)
∂2
f3
∂γ2
+
∂2
f3
∂δ2
+ 2φ
∂2
f3
∂δ∂τ
+ φ2 ∂2
f2
∂τ2
+ r
∂f3
∂γ
= 0
where φ = α(T−t)
2
√
1−ρ2
.
Since α ∼ 10−1
, for maturity date lesser than 1-year the term
(T − t) ∼ 10−1
and (2 1 − ρ2)−1
∼ 10−1
; thus φ ∼ 10−3
, φ2
∼ 10−6
.
Thus it is reasonable to approximate φ 0.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

16. Quantitative Finance: stochastic volatility market models
From Itˇo’s lemma we have:
∂f
∂t
+
1
2
ν S2 ∂2
f
∂S2
+ 2ραS
∂2
f
∂S∂ν
+ α2 ∂2f
∂ν2
+ rS
∂f
∂S
− rf = 0
After three coordinate transformations we have:
∂f3
∂τ
− (1 − ρ2
)
∂2
f3
∂γ2
+
∂2
f3
∂δ2
+ 2φ
∂2
f3
∂δ∂τ
+ φ2 ∂2
f2
∂τ2
+ r
∂f3
∂γ
= 0
where φ = α(T−t)
2
√
1−ρ2
.
Since α ∼ 10−1
, for maturity date lesser than 1-year the term
(T − t) ∼ 10−1
and (2 1 − ρ2)−1
∼ 10−1
; thus φ ∼ 10−3
, φ2
∼ 10−6
.
Thus it is reasonable to approximate φ 0.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

17. Quantitative Finance: stochastic volatility market models
From Itˇo’s lemma we have:
∂f
∂t
+
1
2
ν S2 ∂2
f
∂S2
+ 2ραS
∂2
f
∂S∂ν
+ α2 ∂2f
∂ν2
+ rS
∂f
∂S
− rf = 0
After three coordinate transformations we have:
∂f3
∂τ
− (1 − ρ2
)
∂2
f3
∂γ2
+
∂2
f3
∂δ2
+ 2φ
∂2
f3
∂δ∂τ
+ φ2 ∂2
f2
∂τ2
+ r
∂f3
∂γ
= 0
where φ = α(T−t)
2
√
1−ρ2
.
Since α ∼ 10−1
, for maturity date lesser than 1-year the term
(T − t) ∼ 10−1
and (2 1 − ρ2)−1
∼ 10−1
; thus φ ∼ 10−3
, φ2
∼ 10−6
.
Thus it is reasonable to approximate φ 0.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

18. Quantitative Finance: stochastic volatility market models
This allowed us to illustrate a methodology for solving the pricing PDE
in an approximate way, in which we have imposed to be worthless
some terms of the PDE, recovering a pricing formula which in this
particular case, turn out to be simple, for Vanilla Options and Barrier
Options:
for European Call:
C(t, S, ν) = e
ν(T−t)
4(1−ρ2) S
»
N
“
d1, a0,1
p
1 − ρ2
”
− e
“
−2
ρ
α
ν
”
N
“
d2, a0,2
p
1 − ρ2
”–
− e
ν(T−t)
4(1−ρ2) Ee
−r(T−t)
h
N
“
˜d1, ˜a0,1
p
1 − ρ2
”
− N
“
˜d2, ˜a0,2
p
1 − ρ2
”i
;
for Down-and-out Call:
C
out
L (t, S, ν) = e
−(bρr(T−t))
»
e
cρν(T−t)
N(h1) − e
−
ρν
α(1−ρ2) N(h2)
–
×
8
><
>:
S ∗
2
6
4N(d1) −
„
L
S
« 1−2ρ2
1−ρ2
N(d2)
3
7
5 − e
ν(T−t)
2(1−ρ2) E ∗
"
N(˜d1) −
„
S
L
« 1
1−ρ2
N(˜d2)
#
9
>=
>;
.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

19. Quantitative Finance: stochastic volatility market models
This allowed us to illustrate a methodology for solving the pricing PDE
in an approximate way, in which we have imposed to be worthless
some terms of the PDE, recovering a pricing formula which in this
particular case, turn out to be simple, for Vanilla Options and Barrier
Options:
for European Call:
C(t, S, ν) = e
ν(T−t)
4(1−ρ2) S
»
N
“
d1, a0,1
p
1 − ρ2
”
− e
“
−2
ρ
α
ν
”
N
“
d2, a0,2
p
1 − ρ2
”–
− e
ν(T−t)
4(1−ρ2) Ee
−r(T−t)
h
N
“
˜d1, ˜a0,1
p
1 − ρ2
”
− N
“
˜d2, ˜a0,2
p
1 − ρ2
”i
;
for Down-and-out Call:
C
out
L (t, S, ν) = e
−(bρr(T−t))
»
e
cρν(T−t)
N(h1) − e
−
ρν
α(1−ρ2) N(h2)
–
×
8
><
>:
S ∗
2
6
4N(d1) −
„
L
S
« 1−2ρ2
1−ρ2
N(d2)
3
7
5 − e
ν(T−t)
2(1−ρ2) E ∗
"
N(˜d1) −
„
S
L
« 1
1−ρ2
N(˜d2)
#
9
>=
>;
.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

20. Quantitative Finance: stochastic volatility market models
This allowed us to illustrate a methodology for solving the pricing PDE
in an approximate way, in which we have imposed to be worthless
some terms of the PDE, recovering a pricing formula which in this
particular case, turn out to be simple, for Vanilla Options and Barrier
Options:
for European Call:
C(t, S, ν) = e
ν(T−t)
4(1−ρ2) S
»
N
“
d1, a0,1
p
1 − ρ2
”
− e
“
−2
ρ
α
ν
”
N
“
d2, a0,2
p
1 − ρ2
”–
− e
ν(T−t)
4(1−ρ2) Ee
−r(T−t)
h
N
“
˜d1, ˜a0,1
p
1 − ρ2
”
− N
“
˜d2, ˜a0,2
p
1 − ρ2
”i
;
for Down-and-out Call:
C
out
L (t, S, ν) = e
−(bρr(T−t))
»
e
cρν(T−t)
N(h1) − e
−
ρν
α(1−ρ2) N(h2)
–
×
8
><
>:
S ∗
2
6
4N(d1) −
„
L
S
« 1−2ρ2
1−ρ2
N(d2)
3
7
5 − e
ν(T−t)
2(1−ρ2) E ∗
"
N(˜d1) −
„
S
L
« 1
1−ρ2
N(˜d2)
#
9
>=
>;
.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

21. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a European Call option
r = 3%, ν0 = 0.04, α = 0.1, ρ = −0.64, E = 100,
St = E 1 ± 10%
√
ΘT
T = 1/12
Perturbative method Fourier method for κ = 0
ATM 2.4305 2.4261
INM 2.7337 2.7341
OTM 2.1503 2.1410
T = 3/12
Perturbative method Fourier method for κ = 0
ATM 4.3755 4.3524
INM 4.9037 4.8942
OTM 3.8871 3.8499
T = 6/12
Perturbative method Fourier method for κ = 0
ATM 6.3790 6.3765
INM 7.1214 7.1322
OTM 5.6925 5.6358
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

22. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a European Call option
r = 3%, ν0 = 0.04, α = 0.1, ρ = −0.64, E = 100,
St = E 1 ± 10%
√
ΘT
T = 1/12
Perturbative method Fourier method for κ = 0
ATM 2.4305 2.4261
INM 2.7337 2.7341
OTM 2.1503 2.1410
T = 3/12
Perturbative method Fourier method for κ = 0
ATM 4.3755 4.3524
INM 4.9037 4.8942
OTM 3.8871 3.8499
T = 6/12
Perturbative method Fourier method for κ = 0
ATM 6.3790 6.3765
INM 7.1214 7.1322
OTM 5.6925 5.6358
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

23. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a European Call option
r = 3%, ν0 = 0.04, α = 0.1, ρ = −0.64, E = 100,
St = E 1 ± 10%
√
ΘT
T = 1/12
Perturbative method Fourier method for κ = 0
ATM 2.4305 2.4261
INM 2.7337 2.7341
OTM 2.1503 2.1410
T = 3/12
Perturbative method Fourier method for κ = 0
ATM 4.3755 4.3524
INM 4.9037 4.8942
OTM 3.8871 3.8499
T = 6/12
Perturbative method Fourier method for κ = 0
ATM 6.3790 6.3765
INM 7.1214 7.1322
OTM 5.6925 5.6358
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

24. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a Down-and-out Call option
L = 70, E = 100, St = E 1 ± 10%
√
ΘT
T = 1/12
down-and-out Call Vanilla Call
ATM 1.77384 2.4305
INM 2.0727 2.7337
OTM 1.5048 2.1503
T = 3/12
down-and-out Call Vanilla Call
ATM 3.0715 4.3755
INM 3.5822 4.9037
OTM 2.6123 3.8871
T = 6/12
down-knock-out Call Vanilla Call
ATM 4.3145 6.3790
INM 5.0229 7.1214
OTM 3.6785 5.6925
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

25. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a Down-and-out Call option
L = 70, E = 100, St = E 1 ± 10%
√
ΘT
T = 1/12
down-and-out Call Vanilla Call
ATM 1.77384 2.4305
INM 2.0727 2.7337
OTM 1.5048 2.1503
T = 3/12
down-and-out Call Vanilla Call
ATM 3.0715 4.3755
INM 3.5822 4.9037
OTM 2.6123 3.8871
T = 6/12
down-knock-out Call Vanilla Call
ATM 4.3145 6.3790
INM 5.0229 7.1214
OTM 3.6785 5.6925
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

26. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a Down-and-out Call option
L = 70, E = 100, St = E 1 ± 10%
√
ΘT
T = 1/12
down-and-out Call Vanilla Call
ATM 1.77384 2.4305
INM 2.0727 2.7337
OTM 1.5048 2.1503
T = 3/12
down-and-out Call Vanilla Call
ATM 3.0715 4.3755
INM 3.5822 4.9037
OTM 2.6123 3.8871
T = 6/12
down-knock-out Call Vanilla Call
ATM 4.3145 6.3790
INM 5.0229 7.1214
OTM 3.6785 5.6925
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

27. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a Down-and-out Call option
L = 80, E = 100, St = E 1 ± 10%
√
ΘT
(T = 6/12)
Volatility Perturbative method Fourier method for κ = 0
20% 4.3361 4.3196
ATM 30% 6.4678 6.4593
40% 8.2098 8.4480
20% 5.1092 4.9654
INM 30% 7.6807 7.6785
40% 9.9626 9.9847
20% 3.6172 3.4234
OTM 30% 5.7154 5.7209
40% 6.5834 6.5061
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

28. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a Down-and-out Call option
L = 80, E = 100, St = E 1 ± 10%
√
ΘT
(T = 6/12)
Volatility Perturbative method Fourier method for κ = 0
20% 4.3361 4.3196
ATM 30% 6.4678 6.4593
40% 8.2098 8.4480
20% 5.1092 4.9654
INM 30% 7.6807 7.6785
40% 9.9626 9.9847
20% 3.6172 3.4234
OTM 30% 5.7154 5.7209
40% 6.5834 6.5061
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

29. Quantitative Finance: stochastic volatility market models
Numerical Experiments: for a Down-and-out Call option
L = 80, E = 100, St = E 1 ± 10%
√
ΘT
(T = 6/12)
Volatility Perturbative method Fourier method for κ = 0
20% 4.3361 4.3196
ATM 30% 6.4678 6.4593
40% 8.2098 8.4480
20% 5.1092 4.9654
INM 30% 7.6807 7.6785
40% 9.9626 9.9847
20% 3.6172 3.4234
OTM 30% 5.7154 5.7209
40% 6.5834 6.5061
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

30. Quantitative Finance: stochastic volatility market models
Pricing Error
In order to estimate the error of Perturbative method, we use an
empirical idea. We can evaluate the magnitude of neglected terms,
and we put in relation the magnitude of φ with the pricing error that
we have obtained numerically:
PricingError = F 2φ
∂2
∂δ∂τ
+ φ2 ∂2
∂τ2
f(t, S, ν) ,
where φ = α(T−t)
2
√
1−ρ2
.
Following this approach we are able to conclude that for values of
φ ∼ 10−3
, the price error is around 1% for maturity lesser than 1-year.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

31. Quantitative Finance: stochastic volatility market models
Pricing Error
In order to estimate the error of Perturbative method, we use an
empirical idea. We can evaluate the magnitude of neglected terms,
and we put in relation the magnitude of φ with the pricing error that
we have obtained numerically:
PricingError = F 2φ
∂2
∂δ∂τ
+ φ2 ∂2
∂τ2
f(t, S, ν) ,
where φ = α(T−t)
2
√
1−ρ2
.
Following this approach we are able to conclude that for values of
φ ∼ 10−3
, the price error is around 1% for maturity lesser than 1-year.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

32. Quantitative Finance: stochastic volatility market models
Pricing Error
In order to estimate the error of Perturbative method, we use an
empirical idea. We can evaluate the magnitude of neglected terms,
and we put in relation the magnitude of φ with the pricing error that
we have obtained numerically:
PricingError = F 2φ
∂2
∂δ∂τ
+ φ2 ∂2
∂τ2
f(t, S, ν) ,
where φ = α(T−t)
2
√
1−ρ2
.
Following this approach we are able to conclude that for values of
φ ∼ 10−3
, the price error is around 1% for maturity lesser than 1-year.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

33. Quantitative Finance: stochastic volatility market models
Pricing Error
In order to estimate the error of Perturbative method, we use an
empirical idea. We can evaluate the magnitude of neglected terms,
and we put in relation the magnitude of φ with the pricing error that
we have obtained numerically:
PricingError = F 2φ
∂2
∂δ∂τ
+ φ2 ∂2
∂τ2
f(t, S, ν) ,
where φ = α(T−t)
2
√
1−ρ2
.
Following this approach we are able to conclude that for values of
φ ∼ 10−3
, the price error is around 1% for maturity lesser than 1-year.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

34. Quantitative Finance: stochastic volatility market models
Pricing Error
In order to estimate the error of Perturbative method, we use an
empirical idea. We can evaluate the magnitude of neglected terms,
and we put in relation the magnitude of φ with the pricing error that
we have obtained numerically:
PricingError = F 2φ
∂2
∂δ∂τ
+ φ2 ∂2
∂τ2
f(t, S, ν) ,
where φ = α(T−t)
2
√
1−ρ2
.
Following this approach we are able to conclude that for values of
φ ∼ 10−3
, the price error is around 1% for maturity lesser than 1-year.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

35. Quantitative Finance: stochastic volatility market models
Conclusions
Perturbative method intends to be an alternative method for pricing
options in stochastic volatility market models. We offer an analytical
solution by perturbative expansion in φ, φ = α(T−t)
2
√
1−ρ2
of Heston’s
PDE.
The proposed method has the advantage to compute a solution and
the greeks in closed form, therefore, we have not the problems which
plague the numerical methods. Besides this technique is a general
approach and it can be used for pricing several Derivatives.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

36. Quantitative Finance: stochastic volatility market models
Conclusions
Perturbative method intends to be an alternative method for pricing
options in stochastic volatility market models. We offer an analytical
solution by perturbative expansion in φ, φ = α(T−t)
2
√
1−ρ2
of Heston’s
PDE.
The proposed method has the advantage to compute a solution and
the greeks in closed form, therefore, we have not the problems which
plague the numerical methods. Besides this technique is a general
approach and it can be used for pricing several Derivatives.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

37. Quantitative Finance: stochastic volatility market models
Conclusions
Perturbative method intends to be an alternative method for pricing
options in stochastic volatility market models. We offer an analytical
solution by perturbative expansion in φ, φ = α(T−t)
2
√
1−ρ2
of Heston’s
PDE.
The proposed method has the advantage to compute a solution and
the greeks in closed form, therefore, we have not the problems which
plague the numerical methods. Besides this technique is a general
approach and it can be used for pricing several Derivatives.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models

38. Quantitative Finance: stochastic volatility market models
Conclusions
Perturbative method intends to be an alternative method for pricing
options in stochastic volatility market models. We offer an analytical
solution by perturbative expansion in φ, φ = α(T−t)
2
√
1−ρ2
of Heston’s
PDE.
The proposed method has the advantage to compute a solution and
the greeks in closed form, therefore, we have not the problems which
plague the numerical methods. Besides this technique is a general
approach and it can be used for pricing several Derivatives.
Mario Dell’Era Vanilla Option Pricing in Stochastic Volatility market models