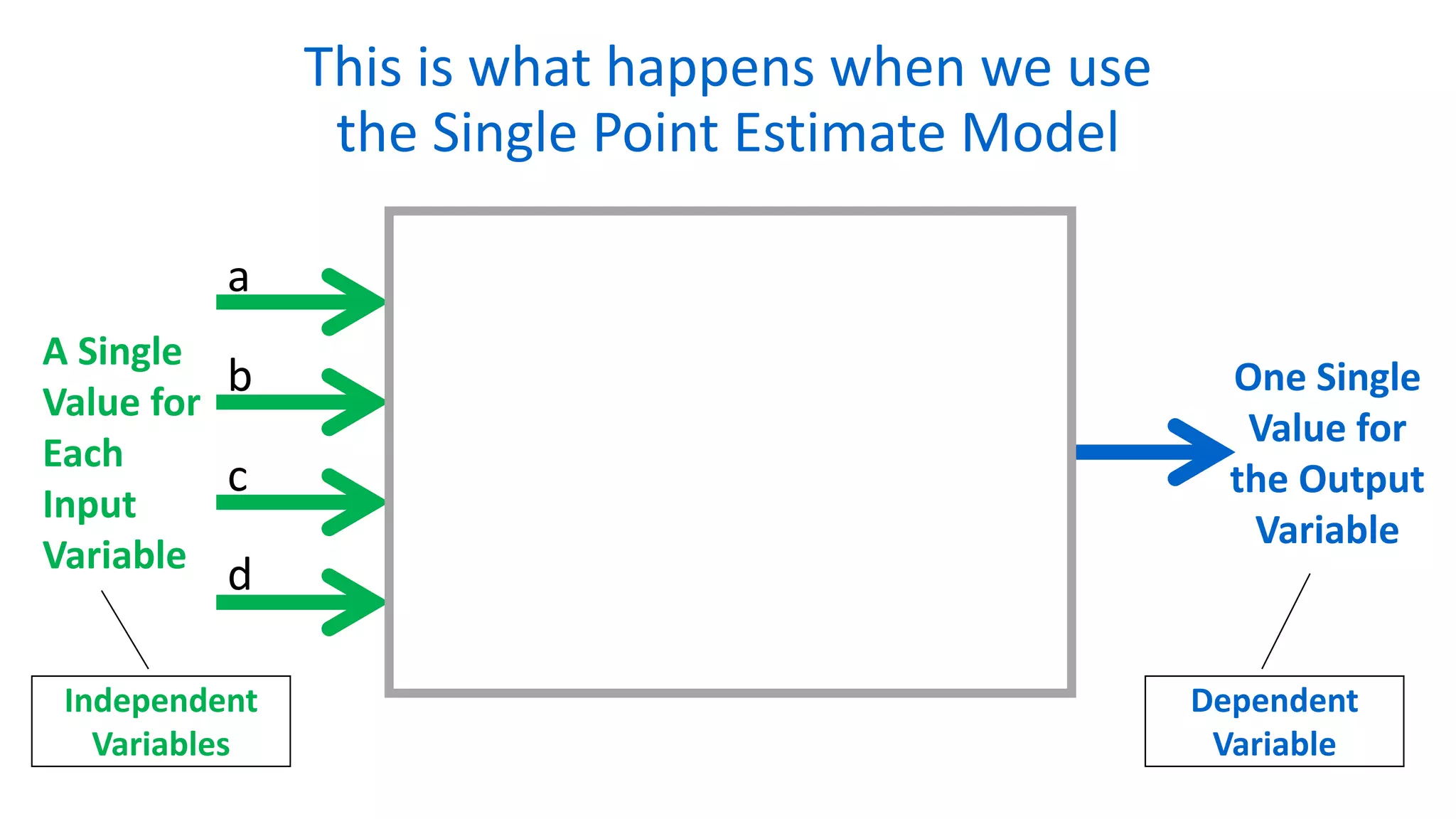
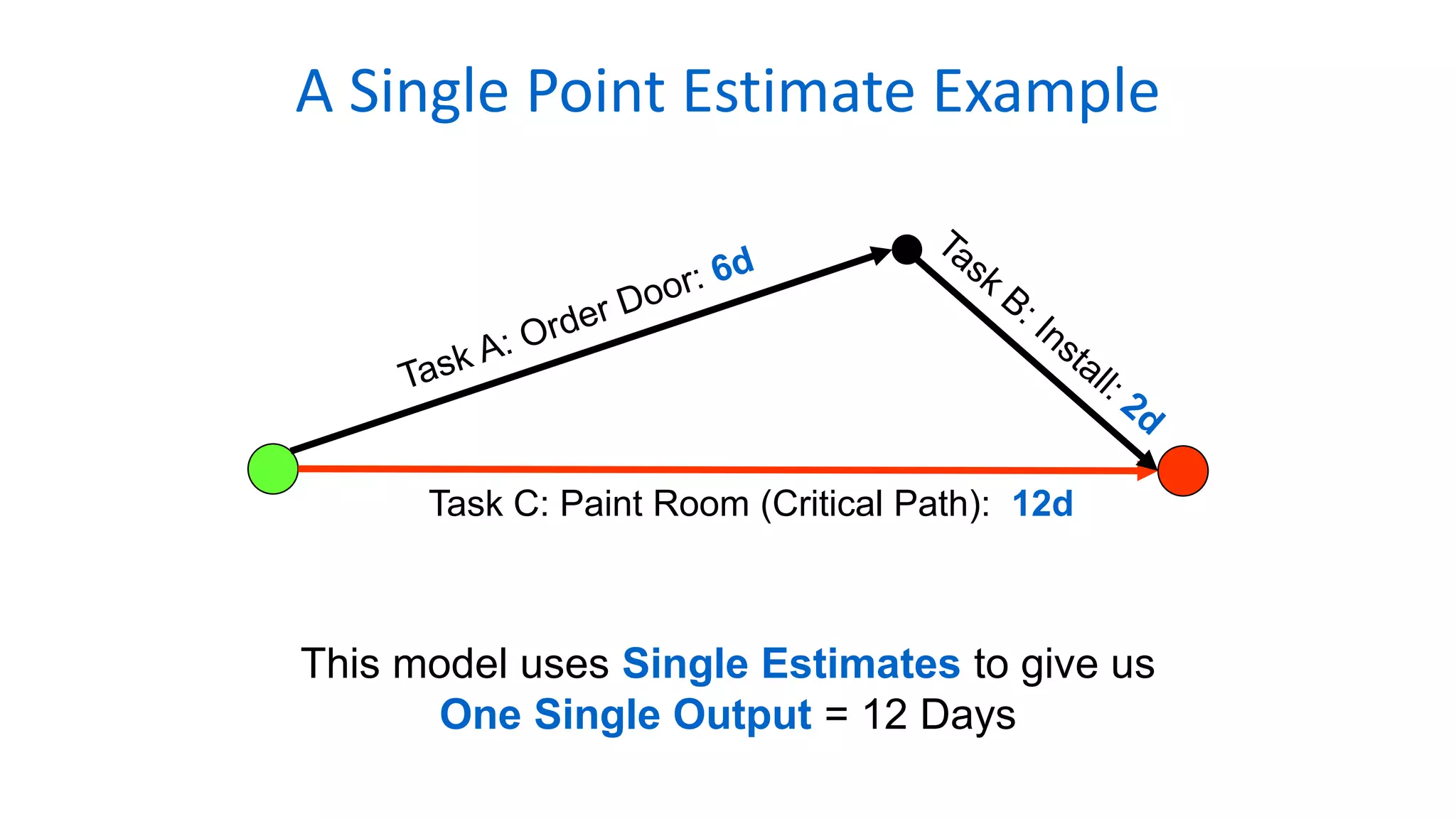
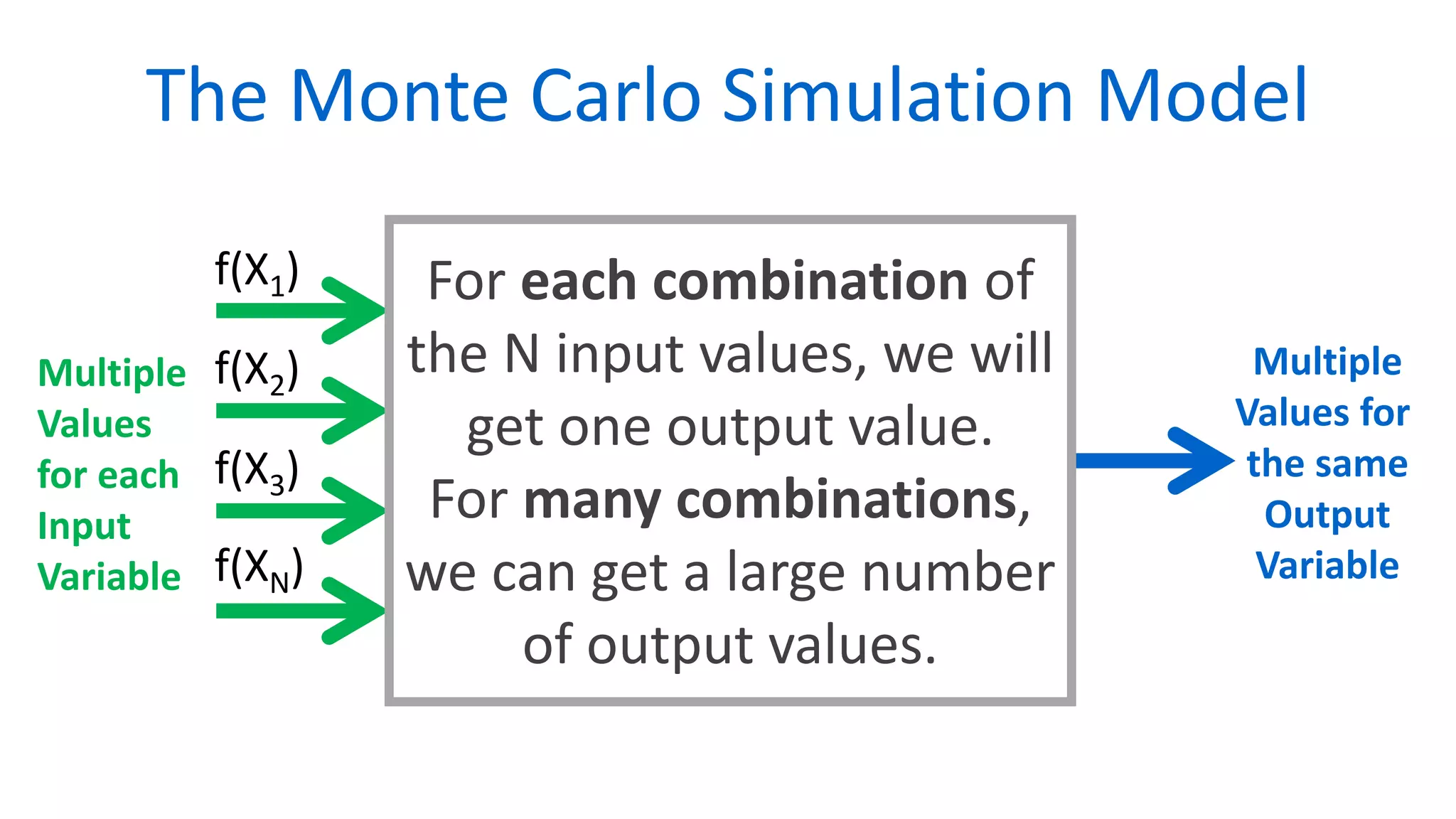
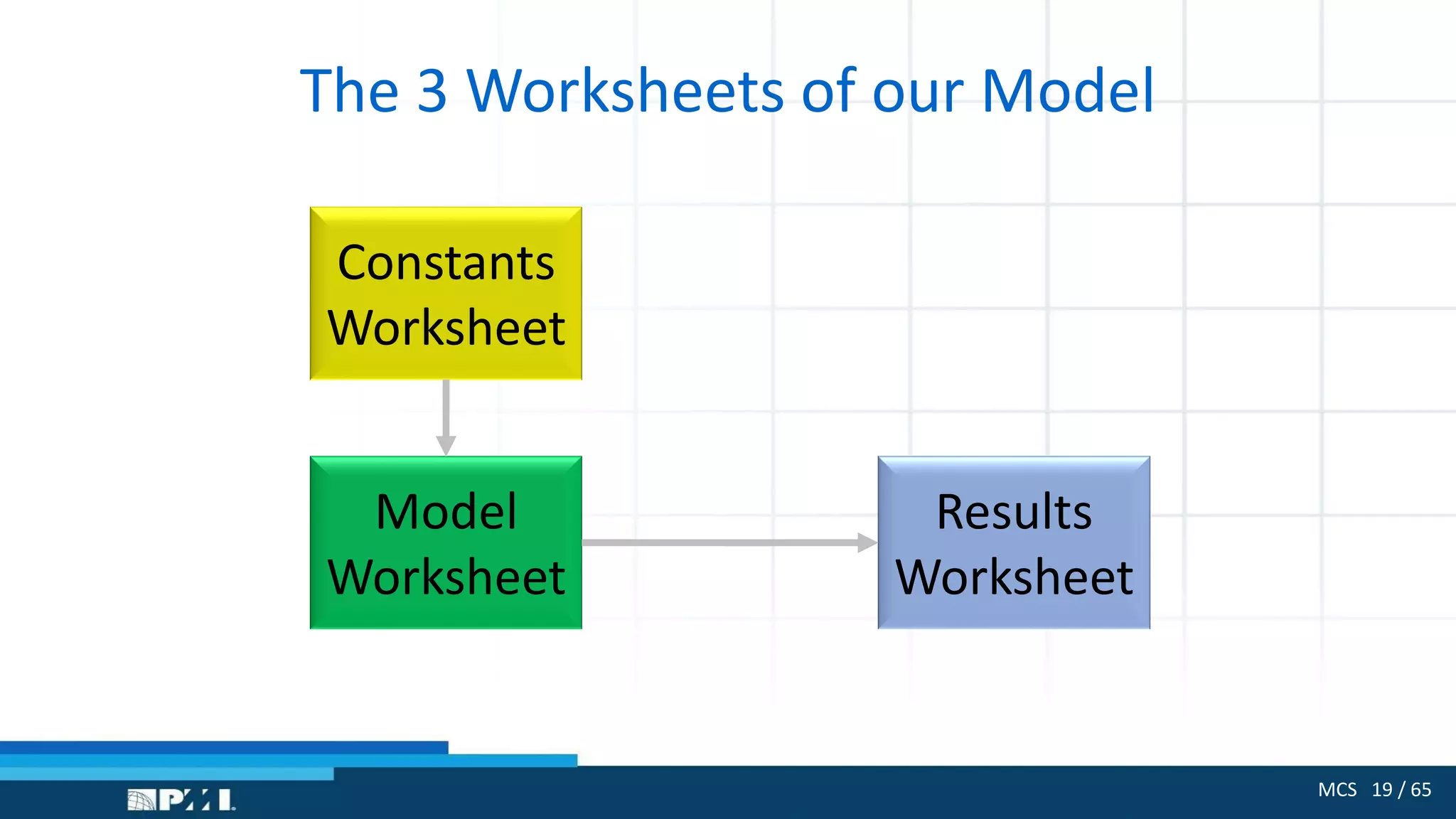
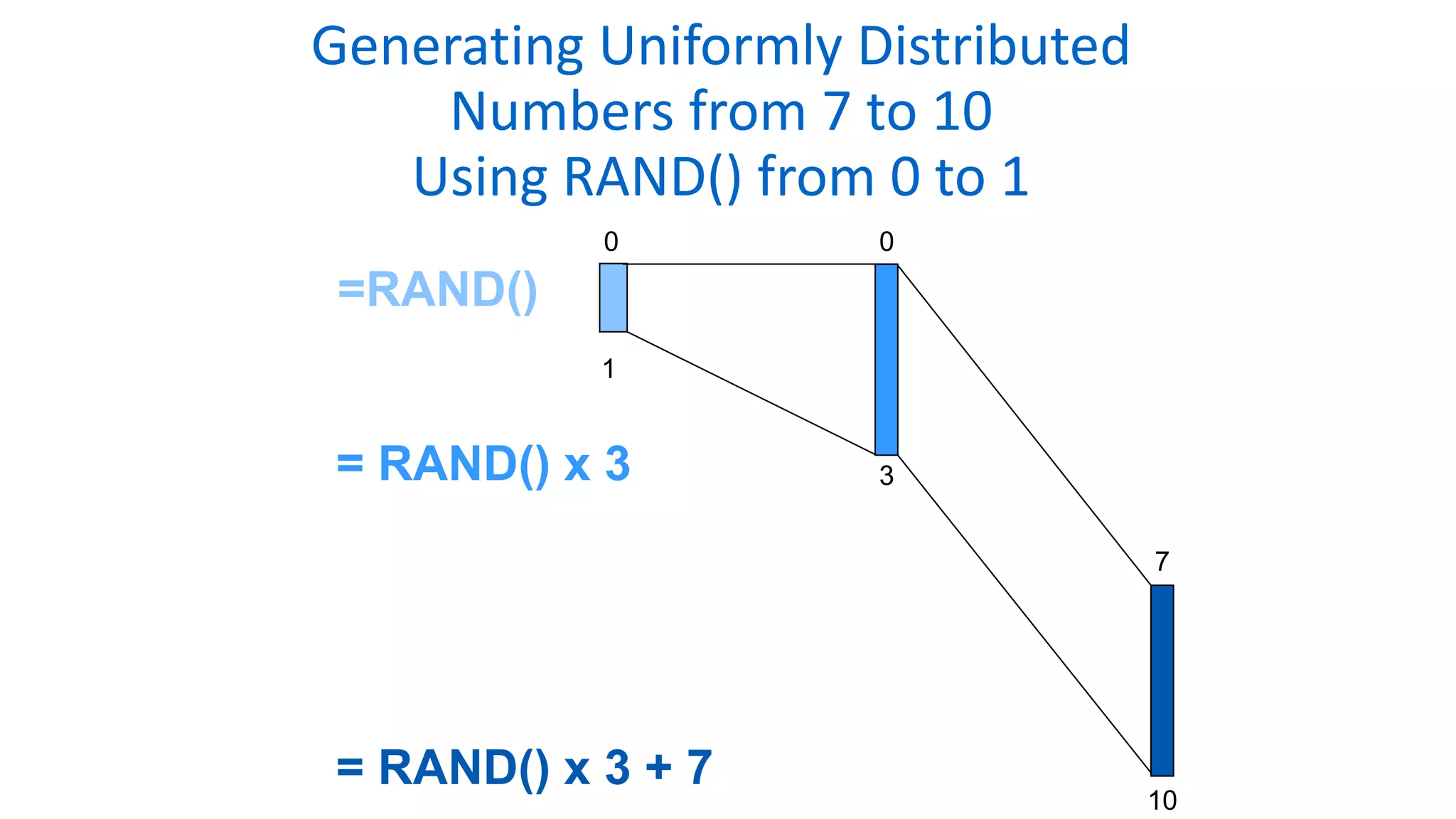
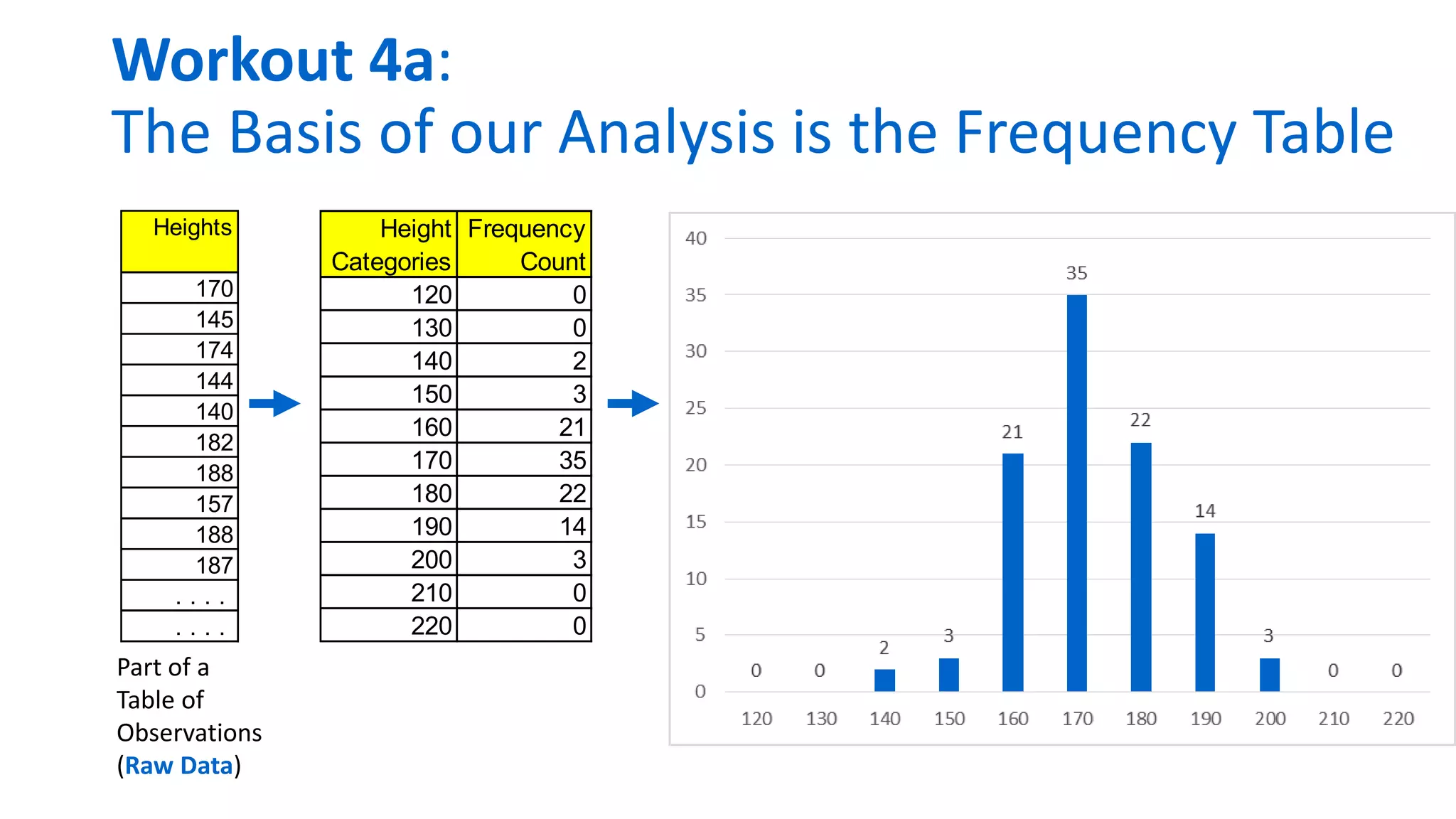
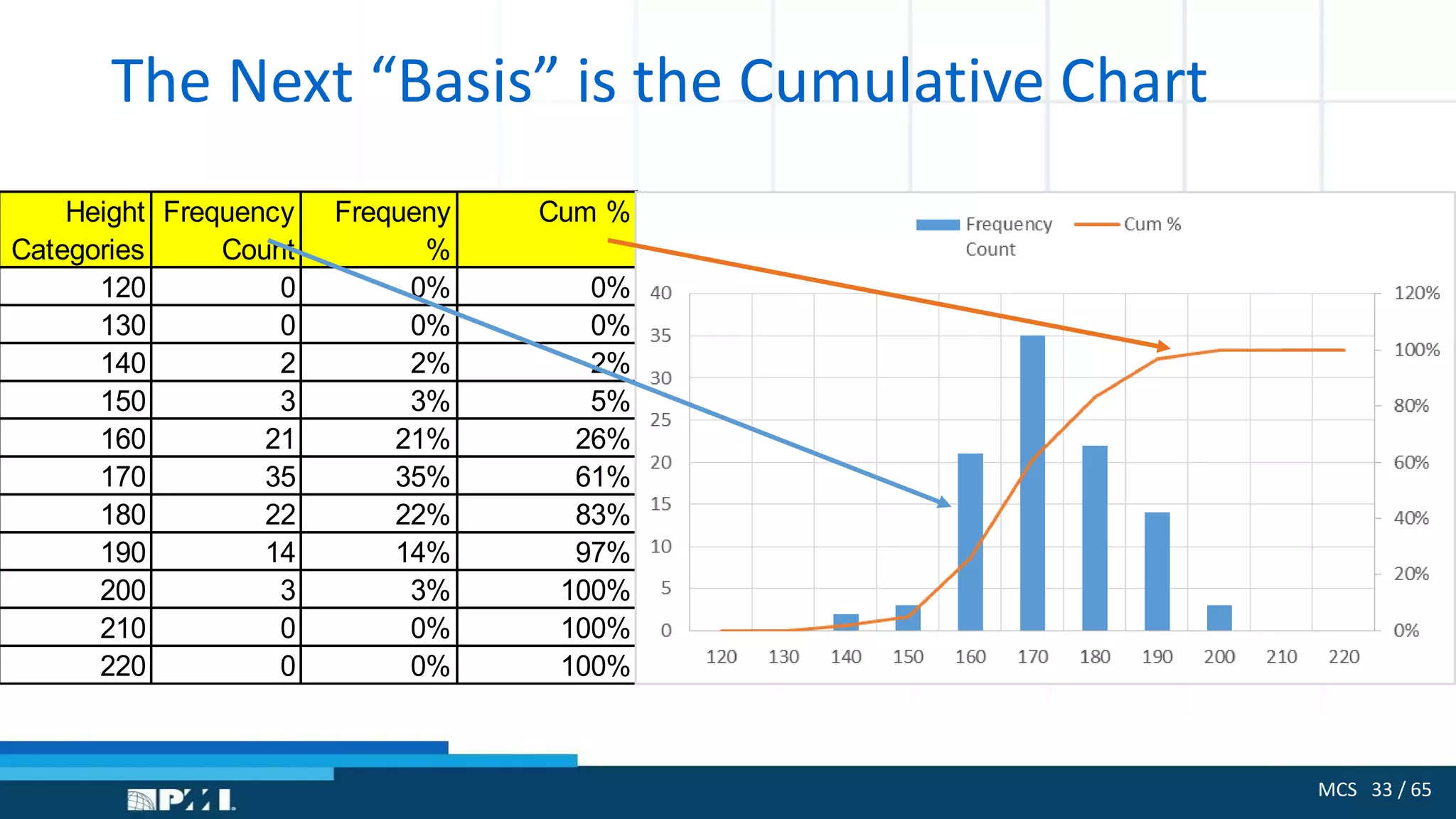
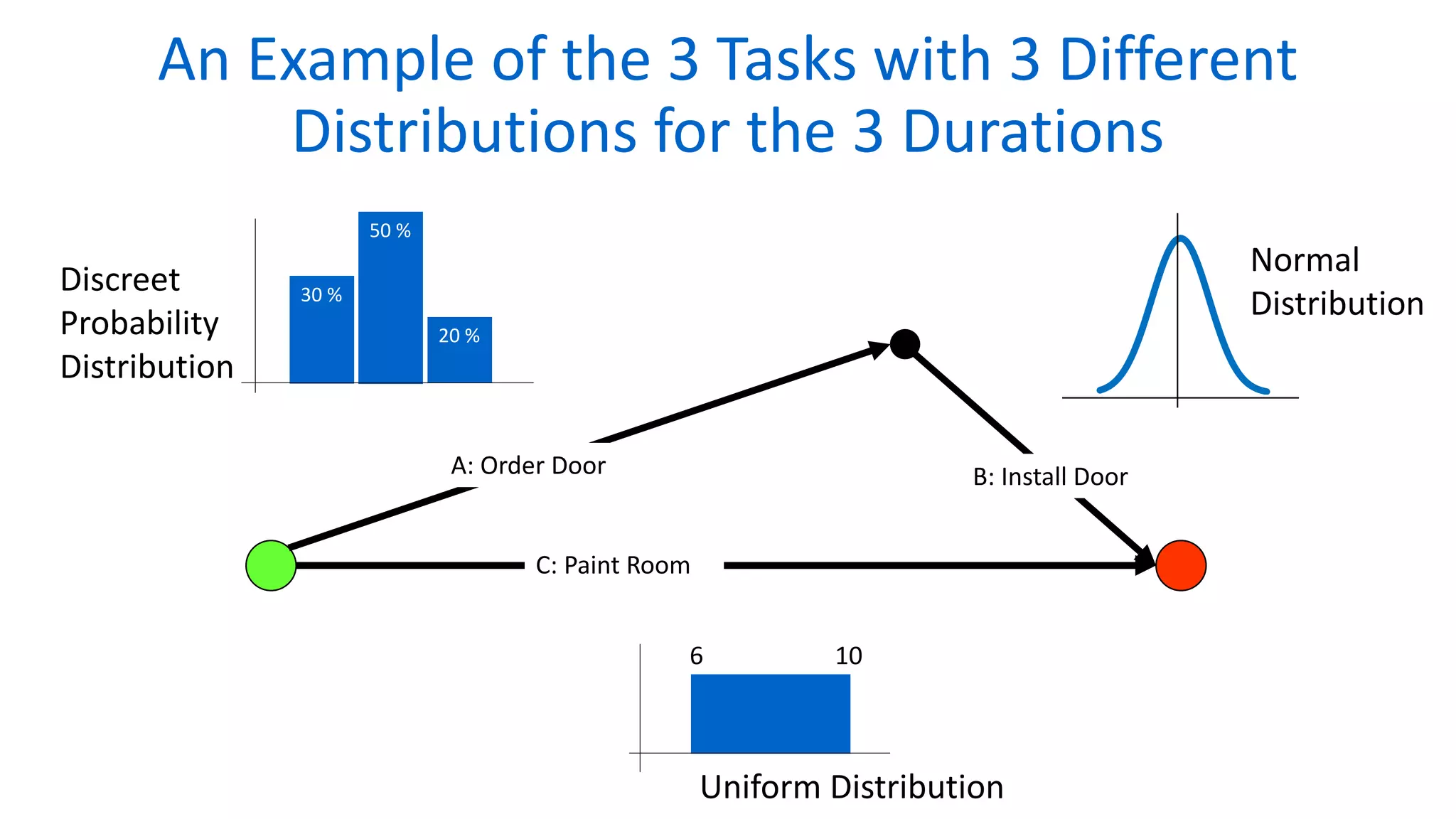
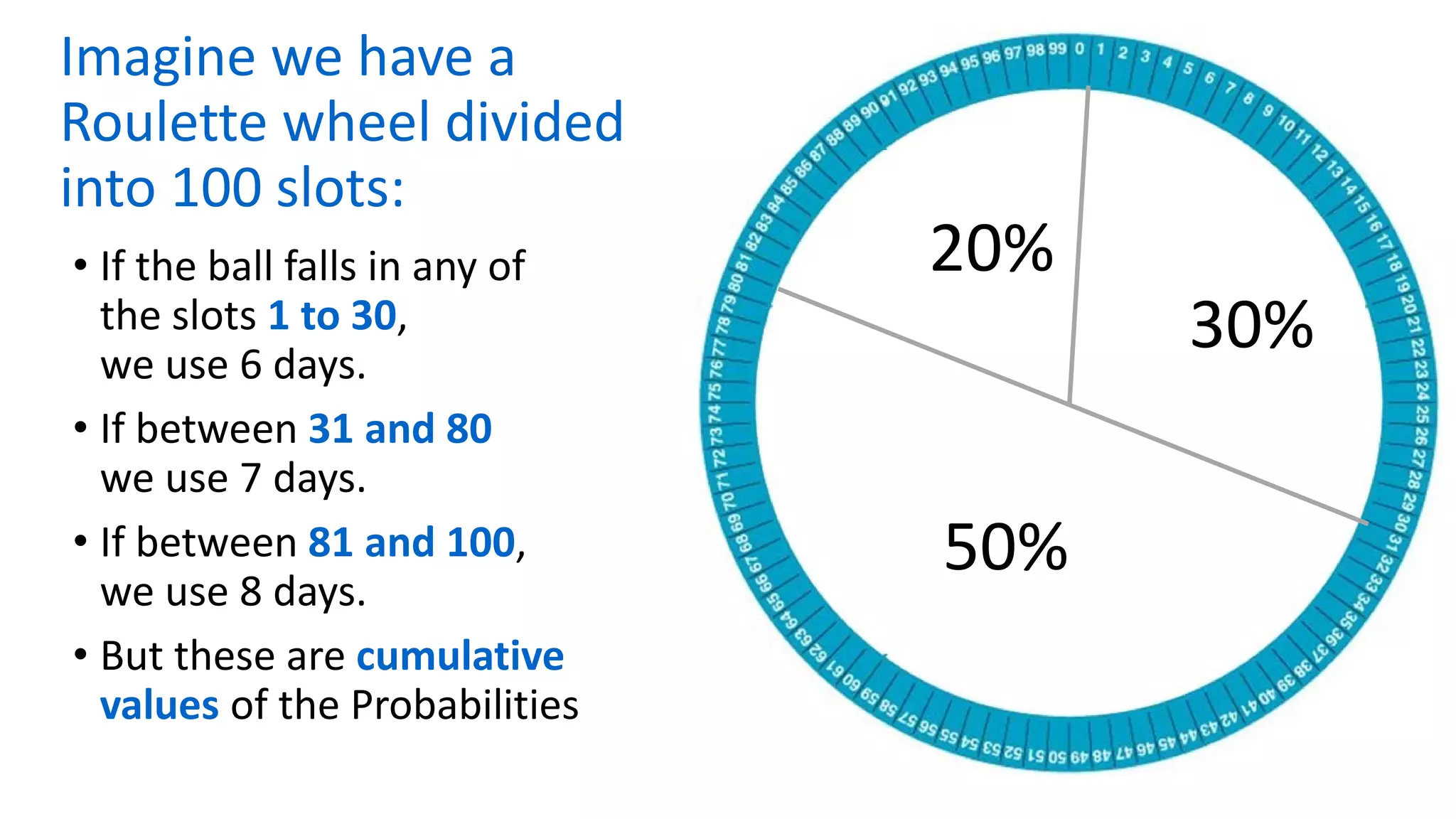
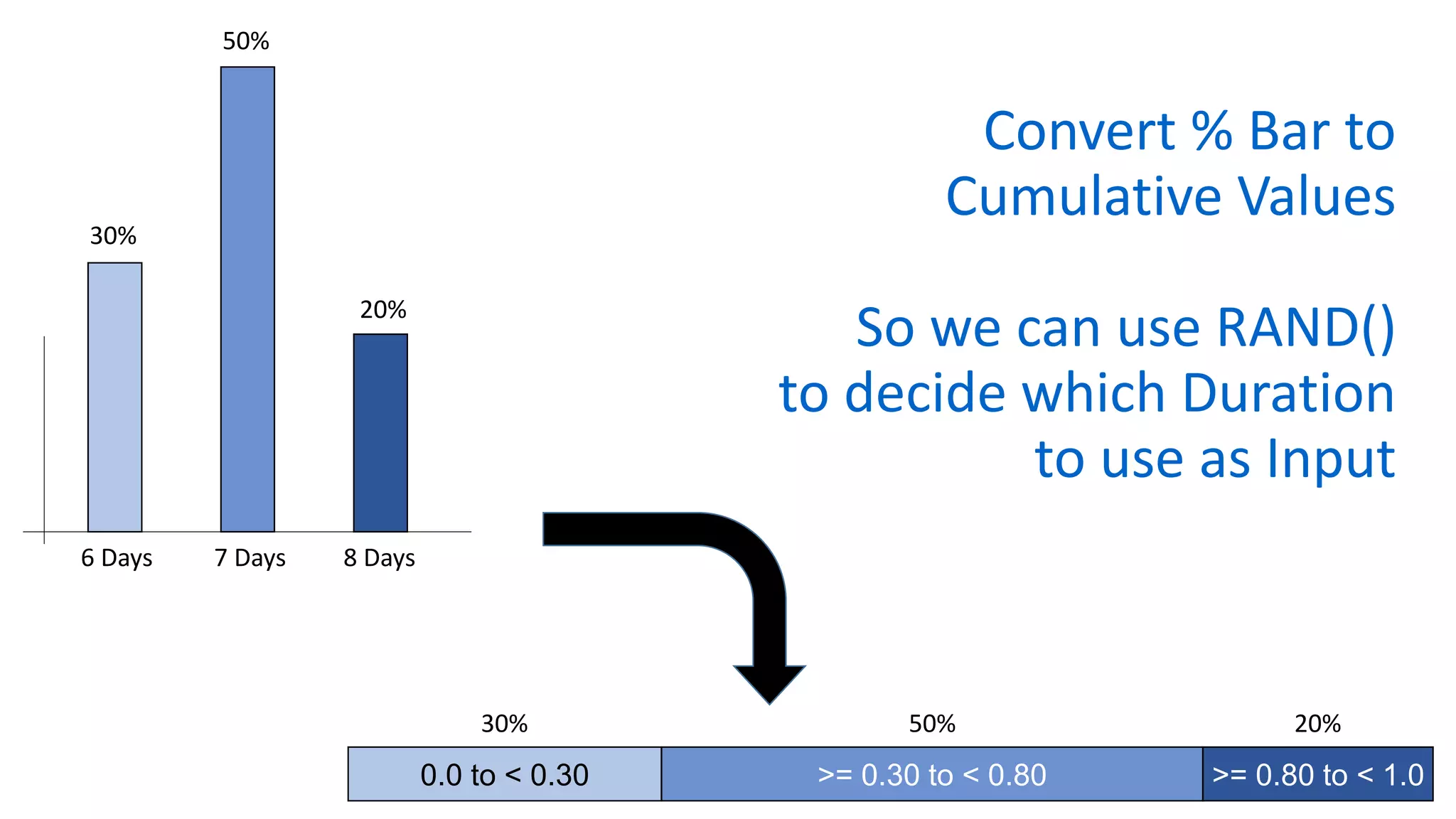
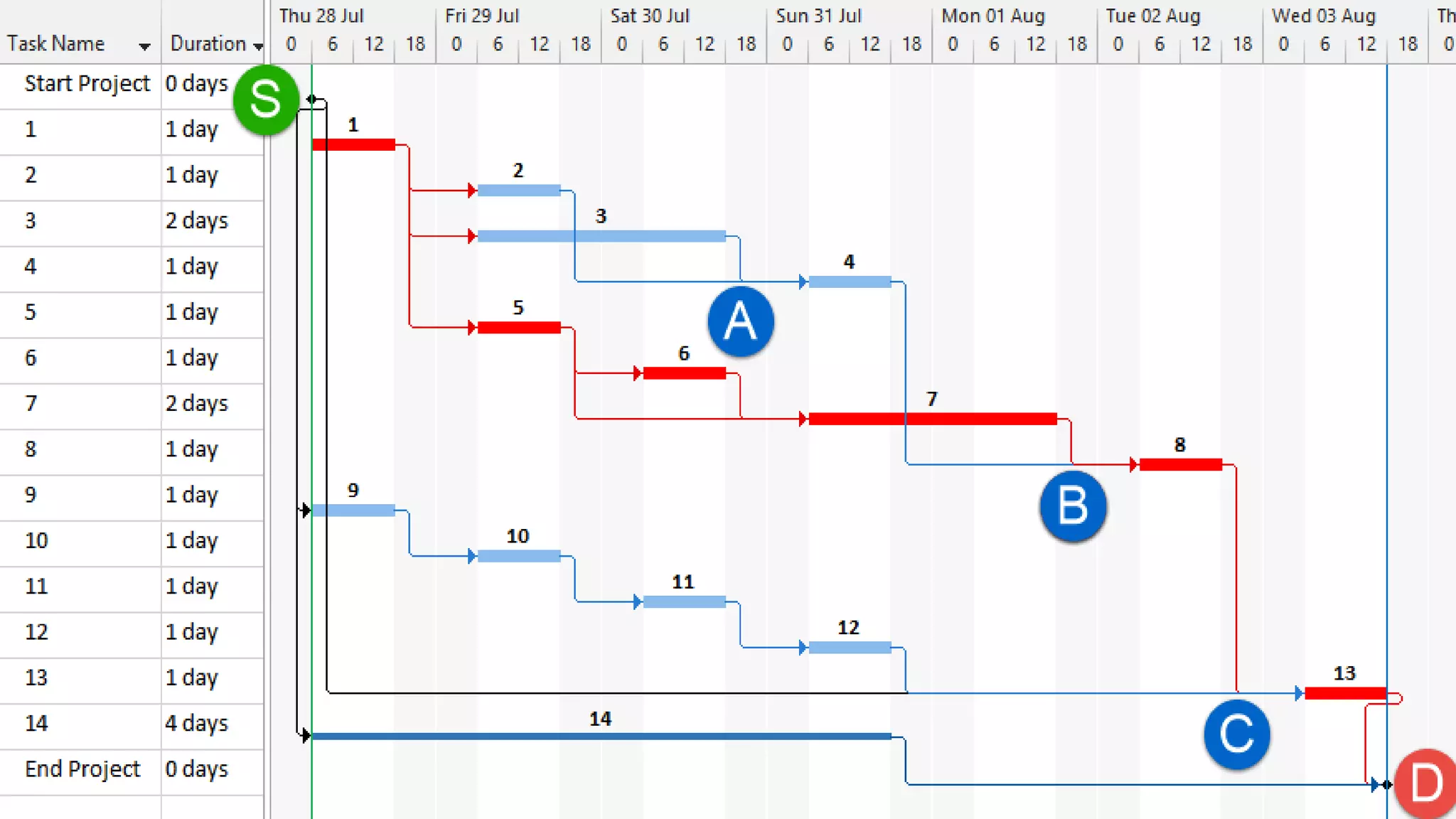
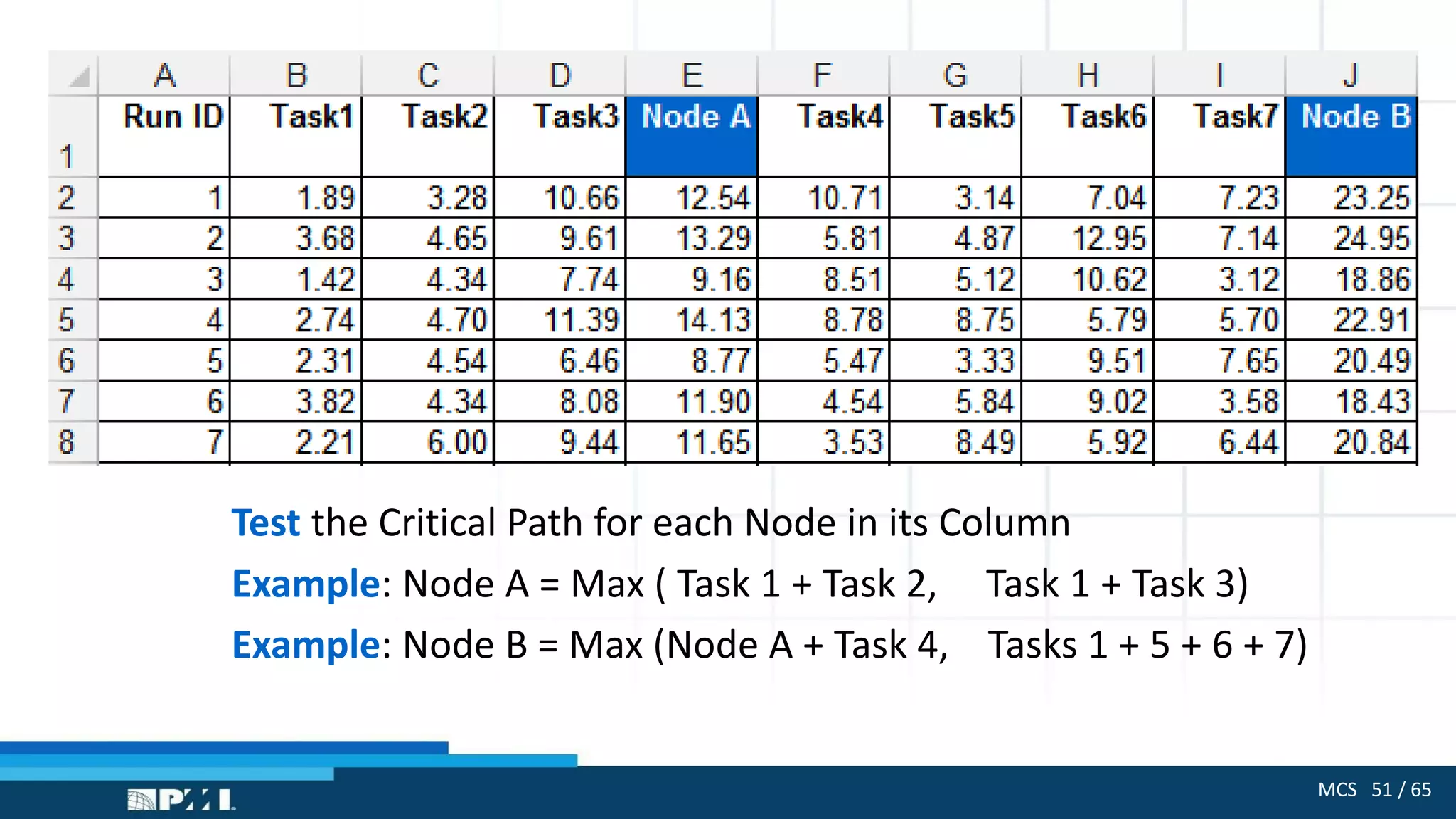
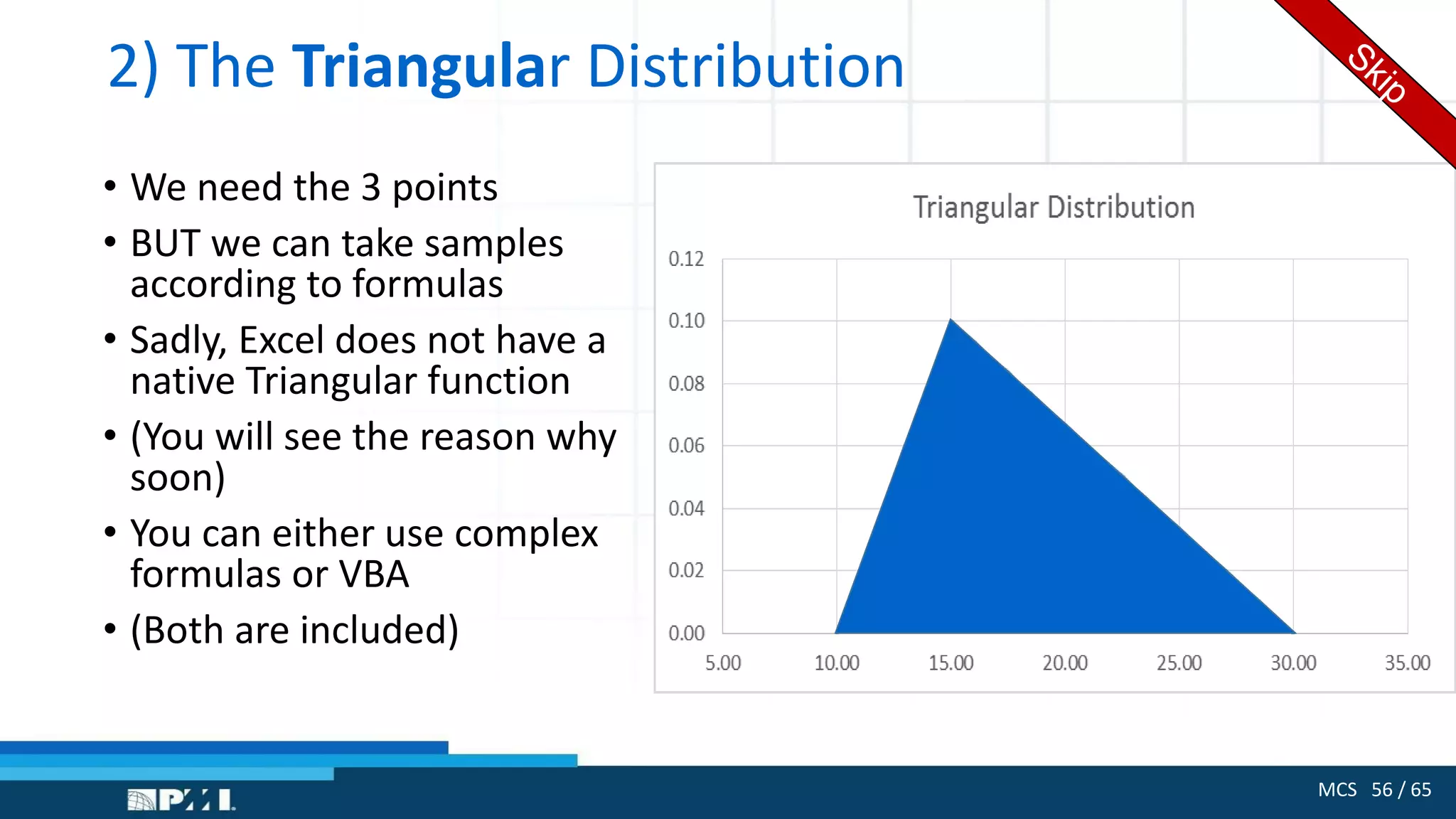
The document outlines the use of Monte Carlo simulation for project estimates, detailing steps for creating models using Excel. It emphasizes the importance of simulating various input values to improve project management forecasts and discusses various distributions for inputs. Additionally, it provides practical workout examples to demonstrate the application of the simulation process in project management.

1. MCS 1 / 65
Using Monte Carlo Simulation
for Project Estimates
Akram Najjar
28 July 2016
Holiday Inn – Dunes
Beirut, Lebanon

2. MCS 2 / 65
First, we state the problem: Why do we need to Simulate?
Second, we discuss the 3 Monte Carlo Simulation Processes:
Process 1: how to prepare a Monte Carlos spreadsheet model
Process 2: how to sample inputs to simulate variety
Process 3: how to analyze the output statistically
10 workouts, will “hopefully” be demonstrated
If time permits: we will demo a Non-PM Monte Carlo Simulations

3. The Handout and ALL Workouts
will be in a Zipped File on
www.pmilebanonchapter.org

4. MCS 4 / 65
Monte Carlo Simulation is also used in other
Management Science applications
• Production lines
• Sales forecast
• Reliability analysis
• Waiting lines (queuing
systems)
• Budget forecasts
• Project Management
•Cost estimations
•Industrial processes
•Project selection
•Acceptance sampling
•Markov chains
•And more . . . .

5. MCS 5 / 65
But first . . . . Why use Excel?
• There are 3rd party Monte Carlo Simulation products
• Very few of them deal directly with Project Management
• I only know one that works directly with Microsoft Project (@RISK)
• BUT
• Excel functions are native, out of the box
• Excel is more flexible (much more so if you write VBA code)
• Excel interacts with other environments better

6. MCS 6 / 65
Off the Shelf Monte Carlo Simulation Tools
• Deals with PM Directly by entering sampling directly on MS Project
• @RISK from PALISADE
• These 2 improve model building but have no direct PM functions
• Crystal Ball from Oracle
• SIMTOOLS Excel Add On
• Focused products that produce simulated schedules
• Acumen Fuse by Deltek
• We can also use VBA with MS Project (which has not been done).

7. MCS 7 / 65
Some Excel Facilities you Need to Know . . . .
• Statistical Functions we will introduce
• Other Excel Functions: COUNTIF, VLOOKUP, etc.
• Absolute/Relative Referencing
• The Analysis Toolpack
• How to produce HISTOGRAMS (Bar Charts or Frequency Count tables)
using the Analysis Toolpack or using =FREQUENCY() and =COUNTIF()
• Advanced Charting (Pareto, Cumulative, etc.)
• Sensitivity analysis
• It helps to know VBA

9. MCS 9 / 65
Why do we Need Monte Carlo Simulation in
Project Management?
• One of the nightmares of a Project Manager is that he / she needs
Single Values for the following:
• Durations
• Resource quantities
• Resource rates
• We call these Single Point Estimates
• The Project Manager has only One Chance to be right . . .
• And he or she will almost never forecast these values correctly . . .

10. I thought you guys were
Working on your
Project Estimates That’s Exactly what we’re
doing . . . . .

11. This is what happens when we use
the Single Point Estimate Model
A Single
Value for
Each
Input
Variable
One Single
Value for
the Output
Variable
a
b
c
d
Independent
Variables
Dependent
Variable

12. Samuel Goldwyn
of MGM
Forecasts are
dangerous,
especially those
about the future.

13. The Oracle of Delphi
Greek Myth
From 1600 BC to 300 BC
A Modern Judgmental
Forecasting Technique

14. A Single Point Estimate Example
Task C: Paint Room (Critical Path): 12d
This model uses Single Estimates to give us
One Single Output = 12 Days

15. Workout 1:
Model with 12 Different Fixed Input Values
• Task A: can be 4 or 8 days
• Task B: can be 1 or 3 days
• Task C: can be 6, 8 or 10 days
• We get: 12 combinations for all inputs
• And 12 results for the Total Duration
• Statistical Analysis of these 12 outputs
will give more reliable and
meaningful estimates
Task A Task B Task C Is Task C Critical? Tot Duration
4 1 6 YES 6
4 1 8 YES 8
4 1 10 YES 10
4 3 6 7
4 3 8 YES 8
4 3 10 YES 10
8 1 6 9
8 1 8 9
8 1 10 YES 10
8 3 6 11
8 3 8 11
8 3 10 11

16. The Monte Carlo Simulation Model
Multiple
Values
for each
Input
Variable
Multiple
Values for
the same
Output
Variable
For each combination of
the N input values, we will
get one output value.
For many combinations,
we can get a large number
of output values.
f(X1)
f(X2)
f(X3)
f(XN)

17. MCS 17 / 65
By using different combinations of values for the input
variables, we will get a large number of values for the
output variable. (The Delphi Oracle?)
We can then analyze the output values statistically.
Our forecast will be “educated” and not a “shot in the
dark”.

18. MCS 18 / 65
Process 1:
How to Setup a Monte Carlo
Spreadsheet to allow the Model
to calculate a large number of
Global Outputs using the large
number of combined Inputs

19. MCS 19 / 65
The 3 Worksheets of our Model
Model
Worksheet
Constants
Worksheet
Results
Worksheet

20. MCS 20 / 65
Our Models will have the Following Structure:
1) Place the parameters or constants in the Constants Worksheet
2) Develop in a One Row a formulation which uses fixed test values.
This calculates a single output for the project.
3) Replace the Fixed Values by Random Samples in the initial row
4) Duplicate the initial Row downwards a large number of times.
The multiple outputs are in one column and are our Raw Results.
We place the above in the Model Worksheet
5) Analyze the Raw Results in the Results Sheet

21. MCS 21 / 65
Workout 2: An Equipment Costing Model
to Demonstrate our Global Procedure
• Row 2 shows the calculation of the total cost using the
Random Samples from a BetaPERT distribution
• The Total Cost =
• Equipment Cost +
• Spares for 3 years +
• Yearly Maintenance = a % of the Cost of the Equipment
• Rows 3 to 1002 duplicate Row 2 to generate 1000 outputs
• Col G is the total cost and has our 1000 Raw Results

22. MCS 22 / 65
Process 2:
How to Use Excel’s Functions
to generate multiple samples
that comply with the behavior
of a specific input f(X1)

23. MCS 23 / 65
Excel’s Statistical Function: = RAND()
• We use Excel’s =RAND() to generate random samples
• It has no argument (no parameters)
• When placed in a cell, it will generate a number
between 0.00000000000000 and 1.00000000000000
• Each number is as likely to be generated as any other.
• We say: the numbers are Uniformly Generated
• Each time you change anything in the worksheet, (or press F9),
RAND() will generate a new number

24. MCS 24 / 65
Workout 3:
Show RAND() is Uniformly Distributed
1) Place “Output” in cell A1
2) Place =RAND() in cells A2:A2001
3) Prepare a Bin Table for values 0.1, 0.2, 0.3 . . . . . . 1.0
4) We will use =COUNTIF() to generate a Histogram for the
2000 values
5) Plot the Bins and Frequency as a Scatter Diagram (Bins vs
Frequency Count)

25. MCS 25 / 65
How to Use RAND()
to Generate Samples
that are Uniformly Distributed
over other ranges than 0 and 1?

26. MCS 26 / 65
What is a Uniform Distribution?
• Many project parameters follow a uniform distribution
• A given input variable would vary from A (lower) to B (upper)
• Each value between A and B is equally likely to arise
• Example:
• A price can range from $10.00 to $14.00 : UNIFORMLY
• The duration of a task can vary from 5.00 to 7.00 days : UNIFORMLY

27. MCS 27 / 65
How to Sample from a Uniform Distribution?
If a Task can have a duration from 7.00 to 10.00 days . . . .
1) RAND() is a Uniform Distribution with values that
vary from 0.0 to 1.0
2) Multiply RAND() by 3 BECAUSE
The duration range = 10 – 7 = 3 days
The generated values will be scaled to vary from 0.0 to 3.0
3) Add 7 to the generated values BECAUSE
The lowest duration = 7
The generated values will be shifted to vary from 7 to 10.

28. Generating Uniformly Distributed
Numbers from 7 to 10
Using RAND() from 0 to 1
0
3
0
1
= RAND() x 3
= RAND() x 3 + 7
7
10
=RAND()

29. MCS 29 / 65
Our Formula for Generating
Uniformly Distributed Values
between A (Lower) and B (Higher):
Generated Value = RAND() * (B – A) + A
= RAND() * Range + A
In Excel, it is best to place A and B in a Constants Sheet
And to calculate the Range = (B – A) to simplify formulas.
The next Workout will demonstrate the use of this formula

30. MCS 30 / 65
Workout 4:
Three Task Project - Uniformly Distributed
1. Use the Duration Ranges in the Earlier Example but let them be uniformly
distributed (i.e., not restricted to integers: fractions allowed).
Duration of Task A is 4 to 8 days
Duration of Task B is 1 to 3 days
Duration of Task C is 6 to 10 days
2. Place the Uniform Distribution formula in cells B2, C2 and D3
3. Use Absolute Values for Constants (to make copying easier)
4. In E1, calculate MAX of (B2 + C2) and D2 = Project Duration (Critical Path)
5. Copy Row 2 downwards to row 2001

31. MCS 31 / 65
Bar Charts, Frequency Tables and Histograms
Are the Same Thing . . . .
Step 1: collect the raw data or results in Col A (Results sheet)
Step 2: specify categories in which we group similar raw data.
These categories are also called: Bins
These can be durations, resource rates or resource quantities
Step 3: use =COUNTIF() to classify our Raw Results into the Bins
Step 4: next to the frequencies of the Bins, find the % Frequency
Step 5: next to the % Frequency, find the Cumulative Frequency %

32. Workout 4a:
The Basis of our Analysis is the Frequency Table
Part of a
Table of
Observations
(Raw Data)
Heights
170
145
174
144
140
182
188
157
188
187
. . . .
. . . .
Height
Categories
Frequency
Count
120 0
130 0
140 2
150 3
160 21
170 35
180 22
190 14
200 3
210 0
220 0

33. MCS 33 / 65
The Next “Basis” is the Cumulative Chart
Height
Categories
Frequency
Count
Frequeny
%
Cum %
120 0 0% 0%
130 0 0% 0%
140 2 2% 2%
150 3 3% 5%
160 21 21% 26%
170 35 35% 61%
180 22 22% 83%
190 14 14% 97%
200 3 3% 100%
210 0 0% 100%
220 0 0% 100%

34. MCS 34 / 65
Workout 5: Repeat the 3 Task Project
with 3 Different Distributions
Task A: Order Door
Duration distributed as a stepwise Discrete Probability Function
Task B: Install Door
Duration distributed Normally (Bell Shaped or Gaussian Curve)
Task C: Paint Room
Duration distributed Uniformly (same as in Workout 4)

35. An Example of the 3 Tasks with 3 Different
Distributions for the 3 Durations
30 %
50 %
20 %
Normal
Distribution
Discreet
Probability
Distribution
Uniform Distribution
A: Order Door B: Install Door
C: Paint Room
6 10

36. MCS 36 / 65
The Logic of Sampling
• In practice: we must analyze every task and decide how it behaves.
• Uniform Behavior (Flat): when the duration depends on load: the more work, the
longer the task --- and we can have any load . . . .
• Discrete Probability (Bars): when durations differ because of different suppliers,
seasons, team members, (but we must know the likelihood).
• Normal Behavior (Bell Shaped): when something is being “built”. The task will have
an average duration with different instances around the average. It also applies to
“behavior” such as delivery.
• Triangular / BetaPERT: when we have and optimistic estimate, a most likely
estimate (mode) and a pessimistic estimate.
• Other Distributions in MCS but not commonly used in PM: Geometric,
Hypergeometric, Exponential, Poisson, Binomial, Weibull, Gamma, etc.

37. How to Use RAND()
to Generate Samples that follow a
Discrete Probability Distribution
30 %
6 days
50 %
7 days
20 %
8 days

38. MCS 38 / 65
What is a Discrete Probability Distribution?
• Inputs may have different values: prices, durations, rates, quantities
• There is a an associated probability for the occurrence of each input
• Example 1 – The Cost Price: 10% of the time, it will be $12.5
while for 40% it will be $13 and for 50% it will be $13.5
• Example 2 – The Duration: sometimes 4 days (35% of the time),
sometimes 6 days (40% of the time) and sometimes 8 days (25%).
• If categories > 4 we have to use =VLOOKUP() else use Nested IF()
• Why? because Nest IF’s gets complicated with more than 4 nests
• Also, you are limited to nest 7 times in an IF() expression

39. Discrete Probabilities for the Duration of
Task A - Order Door:
30% of the time, the Duration will be = 6 days
50% of the time, the Duration will be = 7 days
20% of the time, the Duration will be = 8 days

40. 50%
20%
30%
Imagine we have a
Roulette wheel divided
into 100 slots:
• If the ball falls in any of
the slots 1 to 30,
we use 6 days.
• If between 31 and 80
we use 7 days.
• If between 81 and 100,
we use 8 days.
• But these are cumulative
values of the Probabilities

41. Convert % Bar to
Cumulative Values
So we can use RAND()
to decide which Duration
to use as Input
0.0 to < 0.30 >= 0.30 to < 0.80 >= 0.80 to < 1.0
6 Days 7 Days 8 Days
30%
50%
20%
30% 50% 20%

42. Our example for Task A - Order Door:
1) Probability Col: given to us
2) Cumulative %: calculated by adding
the probabilities cumulatively
3) Duration: given to us
4) In the model, generate a RANDOM
Number between 0 and 1
5) Use nested IF() to find out where it
falls in the CUM % column
6) Pick up the corresponding Duration
Probability Cum % Duration
0.30 0.30 6
0.50 0.80 7
0.20 1.00 8

43. MCS 43 / 65
ALERT: Using RAND() Twice in one Formula
Causes it to be Calculated Twice
• Example: with IF, you cannot test several values against
RAND().
• Each test will result in a different Random Number.
• For such cases, we have to define a special column
containing RAND().
• We can then use its value within the IF Statement

44. MCS 44 / 65
Using NESTED IF() To Generate
Discrete Probability Values
=IF(A2<F2, G2, IF(A2<F3, G3, G4) )

45. MCS 45 / 65
How to Use RAND() to Generate
Samples that are Normally
Distributed (Bell Shaped)

46. MCS 46 / 65
Without Explanation, Let us Use an Excel Formula
=NORM.INV (RAND(), Average, Standard Deviation)
• RAND() feeds the function with Random numbers from 0 and 1
• We have to specify to NORM.INV() the Average of the
distribution and its Standard Deviation
• NORM.INV() will generate a sample or an observation
• If we generate a large number of these observations, they will be
distributed normally as per the average and the standard
deviation

47. MCS 47 / 65
Workout 5a: Show How NORM.INV() Works
1. Enter “Normal” in cell A1
2. Enter “Average” in C1 and “Standard Deviation” in C2
3. Enter the constants 2 in D1 and 0.5 in D2
4. Enter in A2 = NORM.INV(RAND(), $D$1, $D$2)
5. Copy A2 downwards to A1001
6. Create Bins in F1 to F42 varying from 0.0 to 4.0 and generate a
Histogram using = COUNTIF()
7. Plot it . . You should see a Normal Curve (approximately).
The more values you generate, the nearer to the Bell Shaped Curve

48. MCS 48 / 65
Workout 6:
Monte Carlo Simulation
for a Project with 14 Tasks
(And 4 Nodes in the Network)

49. The Microsoft
Project Plan

50. MCS 50 / 65
Mathematically, we Can Define
a Project as Columns in Excel
1. Identify Each Node where parallel paths meet
We have 1 Start Node and 4 other Nodes (and the End Project = D).
2. Create a Column for each Task
3. Create a Column for each Node to be placed after the Tasks that meet
at it.
4. Place the Duration sampling function of each Task in its Column
5. In each Node cell, enter the =MAX() function to find the Critical Path of
the Tasks before it (see next slide for Nodes A and B)

51. MCS 51 / 65
Test the Critical Path for each Node in its Column
Example: Node A = Max ( Task 1 + Task 2, Task 1 + Task 3)
Example: Node B = Max (Node A + Task 4, Tasks 1 + 5 + 6 + 7)

52. MCS 52 / 65
The Logic of the Model
• In Each Model we have to analyze the behavior of EACH Task
• We then decide which Statistical Distribution best describes the
Duration
• For simplicity: we will start with the Uniform Distribution for
ALL tasks - but with different parameters
• We then use the Normal and BetaPERT distributions
• And another model with a Mixture of distributions
• Let us review the Triangular and the BetaPERT Distributions

53. MCS 53 / 65
Workout 6a:
The Triangular and BetaPERT Distributions
• We favor optimistic estimates because of fear, psychology and
managerial pressure
• We might guess the cost of a cubic meter of concrete = $130
• Under fear, psychology and pressure, we will favor a cost = $110
• But we will strongly resist an estimate = $160
• Most LATE projects are really projects which are UNDERESTIMATED
• Most OVER-BUDGET projects are really UNDERESTIMATED

54. MCS 54 / 65
What do we Need for the PERT Estimate, the
Triangular and BetaPERT Distributions?
• We need
• An optimistic estimate
• A most likely estimate
• A pessimistic estimate
• A distribution is positively skewed
if more of its observations are low
• A distribution is negatively skewed
if more of its observations are high

55. MCS 55 / 65
1) The PERT Calculation (Single Estimate)
• You know the most likely duration: M
• You often know the optimistic duration: O
• And the pessimistic: P
Duration = (O + 6 x M + P) / 6
• We used 3 points to calculate our Single Point
• It is better than a Single Point Estimate but not as good as MCS

56. MCS 56 / 65
2) The Triangular Distribution
• We need the 3 points
• BUT we can take samples
according to formulas
• Sadly, Excel does not have a
native Triangular function
• (You will see the reason why
soon)
• You can either use complex
formulas or VBA
• (Both are included)

57. MCS 57 / 65
3) The BetaPERT Function
• Mathematically, this is quite complex but is available in Excel
• Advantage: it does not have a sharp peak
• Advantage: it slopes down smoothly (to the right and to the left)
• We now see why Microsoft did not include the Triangular function
• The 3 parameters have different names in the industry
• The optimistic = minimum
• The most likely = mode
• The pessimistic = maximum

58. The BetaPERT Distribution can have different
Shapes depending on the Mode and other
Parameters
Let us Review Workout 6a
Positively or Left Skewed Negatively or Right Skewed

59. MCS 59 / 65
Workout 7: (if time permits)
Budget Forecasting
• The budget forecast is complex
• It is formulated in the Model worksheet
• Our Input Variables are 8 growth rates varied using different
distributions (found in the Constants worksheet)
• The outputs to be analyzed are then duplicated in the Runs worksheet

60. MCS 60 / 65
Process 3:
How to Use Excel’s Functions
and Charts to Statistically
Analyze the large number of
Outputs generated by the
MCS Model

61. MCS 61 / 65
The Analysis:
1) Convert and Move Dynamic to Static Results
• The Input Data in the Model Sheet is Dynamic
• Because RAND() is found in the formulas, the raw data keeps changing
• When something happens in the Workbook or when we press F9
• The Results in the Model will also be Dynamic
• We cannot analyze Dynamic Results!
• Solution: copy the Results column from the Model to the Result
worksheet
• BUT, Paste as Values, i.e., without formulas
• This freezes the data in the Results worksheet

62. MCS 62 / 65
The Analysis:
2) Prepare a Histogram for the Results
1) Decide on the number of Bins (grouping of results
• Usually from 10 to 30
2) Generate a Frequency Table (Histogram) from the Raw Data using:
• The =FREQUENCY() function OR
• The =COUNTIF() function (only if results are integers) OR
• The Analysis Toolpack (if you are a masochist)
3) Generate the Cumulative % of the Frequency Count
4) Generate the Bar Chart + Cumulative % (Pareto)
• Show a Bar Chart for the Frequency Count (Histogram)
• On the same chart, show the cumulative % of the counts (Pareto)

63. MCS 63 / 65
The Analysis:
3) Show the Descriptive Statistics
• Use the Analysis Toolpack
• Generate the Descriptive Statistics
• These give a variety of analyses about the Raw Data

64. MCS 64 / 65
The Analysis:
4) Manipulate The Model
• Change the constants
• Change the distributions
• Elaborate the calculations
• Why play with the model?
• To verify the results
• To ensure they are close to reality
• To vary the reality model so we can get “What If” sensitivity

65. Thank You!