The document discusses the Totally Asymmetric Simple Exclusion Process (TASEP), a simple interacting particle system introduced in 1975, focusing on large deviations through matrix product representations. It establishes a large deviation principle for the empirical density of a semi-infinite TASEP starting with an empty lattice, providing a convex rate function under certain conditions. The results build on the work of previous researchers and employ matrix analysis to characterize invariant measures related to TASEP.

1. The Semi-In

2. nite TASEP: Large Deviations via
Matrix Products
H. G. Duhart, P. Morters, J. Zimmer
University of Bath
21 November 2014

3. The TASEP
The totally asymmetric simple exclusion process is one of the
simplest interacting particle systems. It was introduced by Liggett
in 1975.
Horacio Gonzalez Duhart TASEP: LDP via MPA

4. The TASEP
The totally asymmetric simple exclusion process is one of the
simplest interacting particle systems. It was introduced by Liggett
in 1975.
Create particles in site 1 at rate 2 (0; 1).
Horacio Gonzalez Duhart TASEP: LDP via MPA

5. The TASEP
The totally asymmetric simple exclusion process is one of the
simplest interacting particle systems. It was introduced by Liggett
in 1975.
Create particles in site 1 at rate 2 (0; 1).
Particles jump to the right with rate 1.
Horacio Gonzalez Duhart TASEP: LDP via MPA

6. The TASEP
The totally asymmetric simple exclusion process is one of the
simplest interacting particle systems. It was introduced by Liggett
in 1975.
Create particles in site 1 at rate 2 (0; 1).
Particles jump to the right with rate 1.
At most one particle per site.
Horacio Gonzalez Duhart TASEP: LDP via MPA

7. The TASEP
The totally asymmetric simple exclusion process is one of the
simplest interacting particle systems. It was introduced by Liggett
in 1975.
Create particles in site 1 at rate 2 (0; 1).
Particles jump to the right with rate 1.
At most one particle per site.
1
. . .
Horacio Gonzalez Duhart TASEP: LDP via MPA

8. The TASEP
Formally, the state space is f0; 1gN and its generator:
Gf () = (1 1)
f (1) f ()
+
X
k2N
k(1 k+1)
f (k;k+1) f ()
Horacio Gonzalez Duhart TASEP: LDP via MPA

9. The TASEP
Theorem (Liggett 1975)
Let be a product measure on f0; 1gN for which
:= lim
k!1
f : k = 1g exists. Then there exist probability
measures %
de

10. ned if either 1
2 and % 1 , or 1
2 and
12
% 1, which are asymptotically product with density %, such
that
if
1
2
then lim
t!1
S(t) =
(
if 1
if 1 ;
and if
1
2
then lim
t!1
S(t) =
8
:
1=2 if
1
2
if
1
2
.
Horacio Gonzalez Duhart TASEP: LDP via MPA

11. Main result
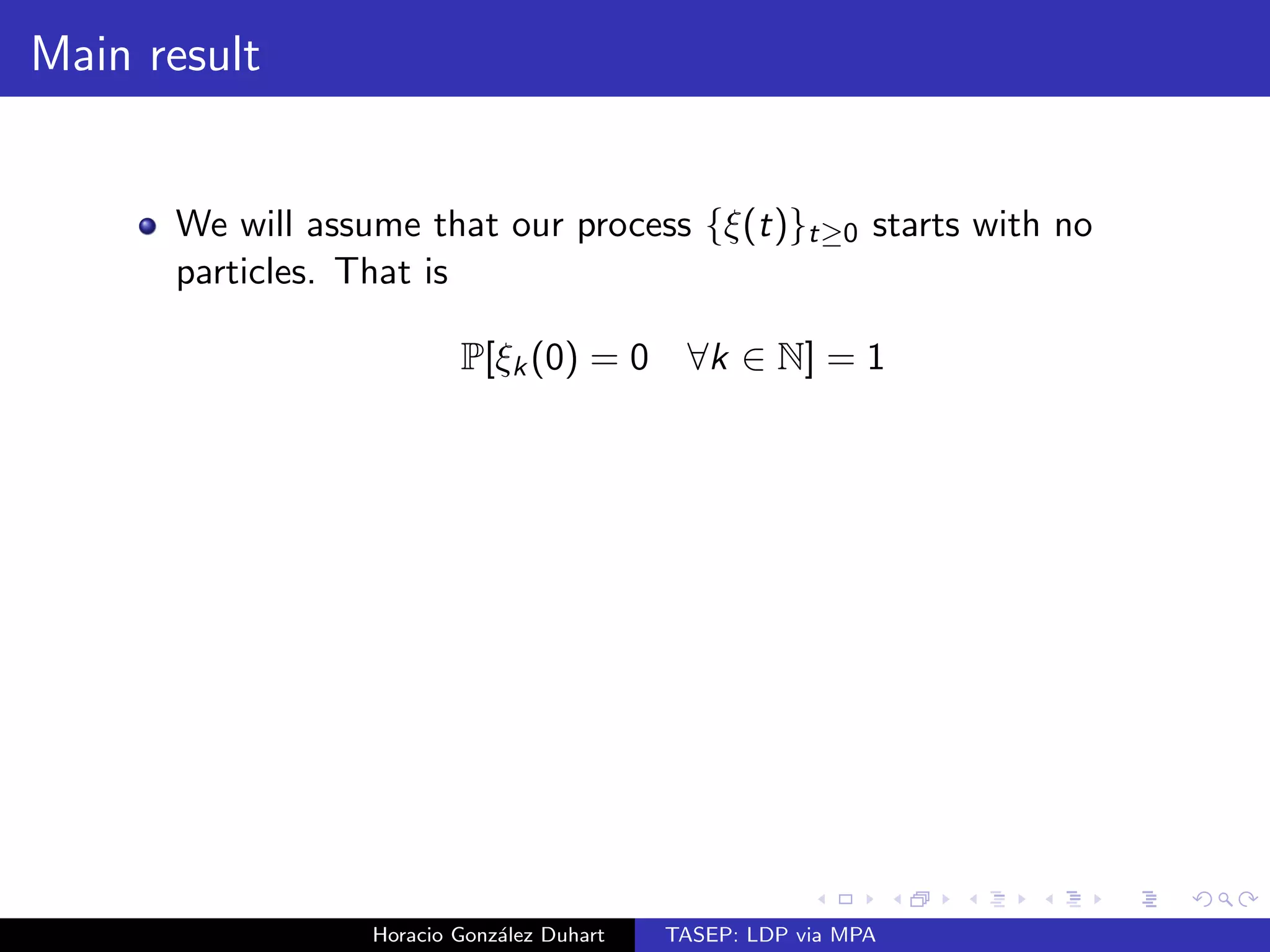
We will assume that our process f(t)gt0 starts with no
particles. That is
P[k(0) = 0 8k 2 N] = 1
Horacio Gonzalez Duhart TASEP: LDP via MPA

12. Main result
We will assume that our process f(t)gt0 starts with no
particles. That is
P[k(0) = 0 8k 2 N] = 1
Working under the reached invariant measure, we will

13. nd a
large deviation principle for the sequence of random variables
fXngn2N of the empirical density of the

14. rst n sites.
Xn =
1
n
Xn
k=1
k
Horacio Gonzalez Duhart TASEP: LDP via MPA

15. Main result
Theorem
Let Xn be the empirical density of a semi-in

16. nite TASEP with
injection rate 2 (0; 1) starting with an empty lattice. Then,
under the invariant probability measure given by Theorem 1,
fXngn2N satis

17. es a large deviation principle with convex rate
function I : [0; 1] ! [0;1] given as follows:
(a) If
1
2
, then I (x) = x log
x
+ (1 x) log
1 x
1
.
(b) If
1
2
, then
I (x) =
8
:
x log
x
+ (1 x) log
1 x
1
+ log (4(1 )) if 0 x 1 ;
2 [x log x + (1 x) log(1 x) + log 2] if 1 x
1
2
;
x log x + (1 x) log(1 x) + log 2 if
1
2
x 1:
Horacio Gonzalez Duhart TASEP: LDP via MPA

18. Main result
Horacio Gonzalez Duhart TASEP: LDP via MPA

19. The MPA
Grokinsky (2004), based on the work of Derrida et. al. (1993),
found a way to completely characterise the measure of Theorem 1
via a matrix representation.
Theorem (Grokinsky)
Suppose there exist (possibly in

20. nite) non-negative matrices D, E
and vectors w and v, ful

21. lling the algebraic relations
DE = D + E; wTE = wT ; c(D + E)v = v
for some c 0. Then the probability measure
c de

22. ned by
c f : 1 = 1; : : : ; n = ng =
wT (
Qn
k=1 kD + (1 k )E) v
wT (D + E)nv
is invariant for the semi-in

23. nite TASEP.
Horacio Gonzalez Duhart TASEP: LDP via MPA

24. The MPA
The invariant measure given by Liggett is the same as the one
given by Grokinsky.
Horacio Gonzalez Duhart TASEP: LDP via MPA

25. The MPA
The invariant measure given by Liggett is the same as the one
given by Grokinsky.
We will focus on the case when we start with an empty lattice.
Horacio Gonzalez Duhart TASEP: LDP via MPA

26. The MPA
12
The invariant measure given by Liggett is the same as the one
given by Grokinsky.
We will focus on the case when we start with an empty lattice.
When , sites behave like iid Bernoulli random variables
with parameter .
Horacio Gonzalez Duhart TASEP: LDP via MPA

27. The MPA
12
The invariant measure given by Liggett is the same as the one
given by Grokinsky.
We will focus on the case when we start with an empty lattice.
When , sites behave like iid Bernoulli random variables
with parameter .
We can

28. nd explicit solutions for the matrices and vectors in
the case 1
2 .
Horacio Gonzalez Duhart TASEP: LDP via MPA

29. The MPA
12
The invariant measure given by Liggett is the same as the one
given by Grokinsky.
We will focus on the case when we start with an empty lattice.
When , sites behave like iid Bernoulli random variables
with parameter .
We can

30. nd explicit solutions for the matrices and vectors in
the case 1
2 .
D =
0
1 1 0 0
0 1 1 0
0 0 1 1
0 0 0 1
BBBBBB@
. . .
...
...
...
...
. . .
1
CCCCCCA
; E =
0
1 0 0 0
1 1 0 0
0 1 1 0
0 0 1 1
BBBBBB@
. . .
...
...
...
...
. . .
1
CCCCCCA
; v =
0
BBB@
1
2
3
...
1
CCCA
;
and wT =
1;
1
1;
1
1
2
;
Horacio Gonzalez Duhart TASEP: LDP via MPA

31. Large deviations
We now want to

32. nd a large deviation principle.
Horacio Gonzalez Duhart TASEP: LDP via MPA

33. Large deviations
We now want to

34. nd a large deviation principle.
Simply put, a sequence of random variables fXngn2N satis

35. es
a LDP with rate function I if
P[Xn x] expfnI (x)g
for some non-negative function I : R ! [0;1]
Horacio Gonzalez Duhart TASEP: LDP via MPA

36. Large deviations
Formally,
De

37. nition (Large deviation principle)
Let X be a Polish space. Let fPngn2N be a sequence of probability
of measures on X. We say fPngn2N satis

38. es a large deviation
principle with rate function I if the following three conditions meet:
i) I is a rate function (non-negative and lsc).
ii) lim sup
n!1
1
n
log Pn[F] inf
x2F
I (x) 8F X closed
iii) lim inf
n!1
1
n
log Pn[G] inf
x2G
I (x) 8G X open:
Horacio Gonzalez Duhart TASEP: LDP via MPA

39. Large deviations
The study of large deviations has been developed since
Varadhan uni

40. ed the theory in 1966.
Horacio Gonzalez Duhart TASEP: LDP via MPA

41. Large deviations
The study of large deviations has been developed since
Varadhan uni

42. ed the theory in 1966.
The result we will use for our proof the Gartner-Ellis Theorem.
Horacio Gonzalez Duhart TASEP: LDP via MPA

43. Large deviations
The study of large deviations has been developed since
Varadhan uni

44. ed the theory in 1966.
The result we will use for our proof the Gartner-Ellis Theorem.
Theorem (Gartner-Ellis)
Let fXngn2N be a sequence of random variables on a probability
space (
;A; P), where
is a nonempty subset of R. If the limit
cumulant generating function : R ! R de

45. ned by
() = lim
n!1
1n
log E[enXn ]
exists and is dierentiable on all R, then fXngn2N satis

46. es a large
deviation principle with rate function I :
! [1;1] de

47. ned by
I (x) = sup
fx ()g:
2R
Horacio Gonzalez Duhart TASEP: LDP via MPA

48. Idea of the proof of the main result
Now the idea is to use the the MPA in calculating the
function in Gartner-Ellis Theorem.
Horacio Gonzalez Duhart TASEP: LDP via MPA

49. Idea of the proof of the main result
Now the idea is to use the the MPA in calculating the
function in Gartner-Ellis Theorem.
() = lim
n!1
1
n
enXn
log E
= lim
n!1
1
n
h
exp
log E
Xn
k=1
k
i
Horacio Gonzalez Duhart TASEP: LDP via MPA

50. Idea of the proof of the main result
Now the idea is to use the the MPA in calculating the
function in Gartner-Ellis Theorem.
() = lim
n!1
1
n
enXn
log E
= lim
n!1
1
n
h
exp
log E
Xn
k=1
k
i
= lim
n!1
1
n
log
X
2f0;1gn
1=4f : k = k for k ng exp
Xn
k=1
k
!
Horacio Gonzalez Duhart TASEP: LDP via MPA

51. Idea of the proof of the main result
Now the idea is to use the the MPA in calculating the
function in Gartner-Ellis Theorem.
() = lim
n!1
1
n
enXn
log E
= lim
n!1
1
n
h
exp
log E
Xn
k=1
k
i
= lim
n!1
1
n
log
X
2f0;1gn
1=4f : k = k for k ng exp
Xn
k=1
k
!
= lim
n!1
1
n
log
wT (eD + E)nv
wT (D + E)nv
Horacio Gonzalez Duhart TASEP: LDP via MPA

52. Idea of the proof of the main result
Now the idea is to use the the MPA in calculating the
function in Gartner-Ellis Theorem.
() = lim
n!1
1
n
enXn
log E
= lim
n!1
1
n
h
exp
log E
Xn
k=1
k
i
= lim
n!1
1
n
log
X
2f0;1gn
1=4f : k = k for k ng exp
Xn
k=1
k
!
= lim
n!1
1
n
log
wT (eD + E)nv
wT (D + E)nv
= lim
n!1
1
n log wT (eD + E)nv 2 log 2:
Horacio Gonzalez Duhart TASEP: LDP via MPA

53. Idea of the proof of the main result
Having the equation
() = lim
n!1
1nlog wT (eD + E)nv 2 log 2
we would like to simplify it and use Gartner-Ellis Theorem.
Horacio Gonzalez Duhart TASEP: LDP via MPA

54. Idea of the proof of the main result
Having the equation
() = lim
n!1
1nlog wT (eD + E)nv 2 log 2
we would like to simplify it and use Gartner-Ellis Theorem.
However, even when we have a explicit form of D, E, v, and
w, the term wT (eD + E)nv is not easy to handle, and so we
split into a lower bound and an upper bound.
Horacio Gonzalez Duhart TASEP: LDP via MPA

55. Upper bound
2s
The upper bound comes from noticing that (eD + E) is a
Toeplitz operator (constant diagonals in the matrix), and v
and w live on a family of weighted spaces `and its dual,
respectively.
Horacio Gonzalez Duhart TASEP: LDP via MPA

56. Upper bound
2s
The upper bound comes from noticing that (eD + E) is a
Toeplitz operator (constant diagonals in the matrix), and v
and w live on a family of weighted spaces `and its dual,
respectively.
We then use Cauchy-Schwarz inequality and optimise over the
parameter s of permissible weights.
wT (eD + E)nv jwj`2?
s
jj(eD + E)njB(`2s
)jvj`2s
Horacio Gonzalez Duhart TASEP: LDP via MPA

57. Lower bound
The lower bound comes from expanding the term
wT (eD + E)nv =
Xn
p=1
Xp
j=0
f n
p;j ()wTEpjDjv
where f n
p;j () are polynomials on e with non-negative
coecients.
Horacio Gonzalez Duhart TASEP: LDP via MPA

58. Lower bound
The lower bound comes from expanding the term
wT (eD + E)nv =
Xn
p=1
Xp
j=0
f n
p;j ()wTEpjDjv
where f n
p;j () are polynomials on e with non-negative
coecients.
We then

59. nd a lower bound when j = 0:
wT (eD + E)nv
Xn
p=1
f n
p;0()wTEpv:
Horacio Gonzalez Duhart TASEP: LDP via MPA

60. Lower bound
The lower bound comes from expanding the term
wT (eD + E)nv =
Xn
p=1
Xp
j=0
f n
p;j ()wTEpjDjv
where f n
p;j () are polynomials on e with non-negative
coecients.
We then

61. nd a lower bound when j = 0:
wT (eD + E)nv
Xn
p=1
f n
p;0()wTEpv:
And another when j = p:
wT (eD + E)nv
Xn
p=1
f n
p;p()wTDpv:
Horacio Gonzalez Duhart TASEP: LDP via MPA

62. Summarising. . .
TASEP: Create particles at rate . Move them to the right at rate 1.
One particle per site.
Horacio Gonzalez Duhart TASEP: LDP via MPA

63. Summarising. . .
TASEP: Create particles at rate . Move them to the right at rate 1.
One particle per site.
MPA: Find matrices and vectors satisfying certain condition to

64. nd the
invariant measure.
Horacio Gonzalez Duhart TASEP: LDP via MPA

65. Summarising. . .
TASEP: Create particles at rate . Move them to the right at rate 1.
One particle per site.
MPA: Find matrices and vectors satisfying certain condition to

66. nd the
invariant measure.
LDP: Find the exponential rate of convergence to 0 of unlikely events.
Horacio Gonzalez Duhart TASEP: LDP via MPA

67. Summarising. . .
TASEP: Create particles at rate . Move them to the right at rate 1.
One particle per site.
MPA: Find matrices and vectors satisfying certain condition to

68. nd the
invariant measure.
LDP: Find the exponential rate of convergence to 0 of unlikely events.
Our result: Find an LDP of the empirical density of the TASEP via the
MPA.
Horacio Gonzalez Duhart TASEP: LDP via MPA

69. Summarising. . .
TASEP: Create particles at rate . Move them to the right at rate 1.
One particle per site.
MPA: Find matrices and vectors satisfying certain condition to

70. nd the
invariant measure.
LDP: Find the exponential rate of convergence to 0 of unlikely events.
Our result: Find an LDP of the empirical density of the TASEP via the
MPA.
Horacio Gonzalez Duhart TASEP: LDP via MPA

71. References
F. den Hollander. Large Deviations, volume 14 of Fields Institute
Monographs. American Mathematical Society, Providence, RI, 2000.
B. Derrida, M. R. Evans, V. Hakim, and V. Pasquier. Exact solution
of a 1D asymmetric exclusion model using a matrix formulation. J.
Phys. A, 26(7):1493,1993.
S. Grokinsky. Phase transitions in nonequilibrium stochastic
particle systems with local conservation laws. PhD thesis, TU
Munich, 2004.
T. M. Liggett. Ergodic theorems for the asymmetric simple
exclusion process. Trans. Amer. Math. Soc., 213:237-261,1975.
H. G. Duhart, P. Morters, and J. Zimmer. The Semi-In

72. nite
Asymmetric Exclusion Process: Large Deviations via Matrix
Products. ArXiv e-prints, arXiv:1411.3270v1, November 2014.
Horacio Gonzalez Duhart TASEP: LDP via MPA

73. Functional Materials Far From Equilibrium
21 November 2014, University of Bristol