Trigonometry 10th edition larson solutions manual

Trigonometry 10th Edition Larson SOLUTIONS MANUAL
Full download:
https://testbanklive.com/download/trigonometry-10th-edition-larson-
solutions-manual/
C H A P T E R 2
Analytic Trigonometry
Section 2.1 Using Fundamental Identities ............................................................213
Section 2.2 Verifying Trigonometric Identities....................................................221
Section 2.3 Solving Trigonometric Equations......................................................227
Section 2.4 Sum and Difference Formulas...........................................................242
Section 2.5 Multiple-Angle and Product-to-SumFormulas ................................258
Review Exercises ........................................................................................................270
Problem Solving .........................................................................................................281
Practice Test .............................................................................................................288

© 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 213
2
4
= −
= −

2
5
3
= −
= −
= −


C H A P T E R 2
Section 2.1 Using Fundamental Identities
1. tan u
2. csc u
9. sin θ
3
= − , cos θ
4
> 0 θ is in Quadrant IV.
3 9 7
3. cot u
cos θ = 1 − − =

−
3
1 − =
16 4
4. csc u
tan θ =
sin θ
= 4 = −
3 3 7
5. 1
cos θ 7 7 7
4
6. −sin u sec θ
1 1 4
= = = =
4 7
7. sec x
5
, tan x < 0 x is in Quadrant II.
cos θ 7 7 7
4
2 cot θ
1 1 7
= = = −
cos x =
1
=
1
= −
2 tan θ −
3 3
7
sec x
−
5 5
2 csc θ
1 1 4
= = = −
sin x = 1 − −
2
=

1 −
4
=
21
25 5
sin θ −
3 3
4
2
tan x =
sin x
21
= 5 = −
21
10. cos θ = , sin θ
3
< 0 θ is in Quadrant IV.
2
cos x −
2 2 sin θ = − 1 −
2
= − 1 −
4
= −
5
5
csc x =
1
=
5
=
5 21

9 3
−
5
sin x 21 21 tan θ =
sin θ
= 2 = −
5
cot x =
1
= −
2
= −
2 21
cos θ 2 2
3
tan x 21 21 1 1 3
8. csc x
7
, tan x > 0 x is in Quadrant III.
secθ =
cos θ
=
2
=
2
3
6
cot θ =
1
=
1
= −
2 2 5
sin x =
1
=
1
= −
6 tan θ
−
5 5 5
csc x
−
7 7
6
cscθ
2
=
1
=
1
= −
3 3 5


2
7
cos x = − 1 − −
6

−
6
= − 1 −
36
= −
13
49 7
sin θ
−
5 5 5
3
tan x =
sin x
cos x
= 7 =
6
=
−
13 13
6 13
13
7
sec x =
1
=
1
= −
7
= −
7 13
cos x
−
13 13 13
7
cot x =
1
=
1
=
13
tan x 6 6
13

© 2018 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.

2
2
2
csc x = − 1 +
7
= −

= −
cos x 
2
214 Chapter 2 Analytic Trigonometry
11. tan x =
2
, cos x > 0 x is in Quadrant I. 15. cos x(1 + tan2
x) = cos x(sec2
x)
3 1
cot x =
1
=
1
=
3 = cos x
cos2
x
tan x 2 2
3
2 4 13
=
1
cos x
= sec x
sec x = 1 + =
3
3
1 + =
9 3
9 13
Matches (f).
cos x 1 1
csc x = 1 + = 1 + = 16. cot x sec x = ⋅ = = csc x
2 4 2 sin x cos x sin x
sin x =
1
=
1
=
2
=
2 13 Matches (a).
csc x 13 13 13
sec2
x − 1 tan2
x sin2
x 1
2 17. = = ⋅ = sec2
x
cos x =
1
=
1
=
3
=
3 13 sin2
x sin2
x cos2
x sin2
x
sec x 13 13 13
3
Matches (e).
cos2
(π 2) − x sin2
x sin x
cot x =
1
=
1
=
3 18.
cos x
=
cos x
= sin x = tan x sin x
cos x
tan x 2 2
3 Matches (d).
12. cot x =
7
, sin x < 0 x is in Quadrant III.
4
19.
tan θ cot θ
1 
tan θ 
=
tan θ
tan x =
1
=
1
=
4 secθ 1
cot x 7 7
4
4 16 65
cos θ
=
1
1
sec x = − 1 + = −
7
2

= −
1 + = −
49 7
1 +
49
= −
65
π

cos θ
= cos θ
4 16 4 20. cos − x sec x = sin x sec x
sin x =
1
=
1
= −
4 4 65 2 
1
csc x
−
65 65 65
4
= sin x
cos x
cos x =
1
=
1
= −
7 7 65 = tan x
sec x
−
65 65 65
7
21. tan2
x − tan2
x sin2
x = tan2
x(1 − sin2
x)
= tan2
x cos2
x
2
13. sec x cos x =
1
cos x

=
sin x
⋅ cos2
x
cos2
x
= 1
Matches (c).
22.

=
s
i
n
2
x
sin2
x sec2
x − sin2
x = sin2
x(sec2
x − 1)
14. cot2
x − csc2
x = (csc2
x − 1) − csc2
x
= −1
= sin2
x tan2
x
Matches (b).
23.
sec x − 1
=
(sec x + 1)(sec x − 1)
sec x − 1 sec x − 1
= sec x + 1
24.
cos x − 2
=
cos x − 2
cos2
x − 4 (cos x + 2)(cos x − 2)
=
1
cos x + 2

= −
2
Section 2.1 Using Fundamental Identities 215
25. 1 − 2 cos x + cos x = (1 − cos x) 26. sec4
x − tan4
x = (sec2
x + tan2
x)(sec2
x − tan2
x)
2 4 2
2
( 2 2
)( )
= (sin2
x) = sec x + tan x 1
27.
28.
= sin4
x
cot3
x + cot2
x + cot x + 1 = cot2
x(cot x + 1) + (cot x + 1)
= (cot x + 1)(cot2
x + 1)
= (cot x + 1)csc2
x
sec3
x − sec2
x − sec x + 1 = sec2
x(sec x − 1) − (sec x − 1)
= (sec2
x − 1)(sec x − 1)
= tan2
x(sec x − 1)
= sec2
x + tan2
x
29. 3 sin2
x − 5 sin x − 2 = (3 sin x + 1)(sin x − 2) 38. cot u sin u + tan u cos u =
cos u
(sin u) +
sin u
(cos u)
30. 6 cos2
x + 5 cos x − 6 = (3 cos x − 2)(2 cos x + 3)
sin u
= cos u + sin u
cos u
2 2 2
31. cot2
x + csc x − 1 = (csc2
x − 1) + csc x − 1 39.
1 − sin x
=
cos x
= cos2
x tan2
x = (cos2
x)
sin x
2 2 2
= csc2
x + csc x − 2
= (csc x − 1)(csc x + 2)
csc x − 1 cot x
= sin2
x
cos x
32. sin2
x + 3 cos x + 3 = (1 − cos2
x) + 3 cos x + 3
= −cos2
x + 3 cos x + 4
= −(cos2
x − 3 cos x − 4)
= −(cos x + 1)(cos x − 4)
40.
cos2
y
1 − sin y
1 − sin2
y
=
1 − sin y
=
(1 + sin y)(1 − sin y)
1 − sin y
= 1 + sin y
33. tan θ csc θ =
sin θ
⋅
1
=
1
= secθ
41. (sin x + cos x)
2
= sin2
x + 2 sin x cos x + cos2
x
= (sin2
x + cos2
x) + 2 sin x cos x
cos θ sin θ cos θ = 1 + 2 sin x cos x
34. tan(−x) cos x = −tan x cos x
sin x
⋅ cos x
cos x
= −sin x
42. (2 csc x + 2)(2 csc x − 2) = 4 csc2
x − 4
= 4(csc2
x − 1)
= 4 cot2
x
35. sin φ(csc φ − sin φ) = (sin φ)
1
− sin2
φ 43.
1
+
1
=
1 − cos x + 1 + cos x
sin φ 1 + cos x 1 − cos x (1 + cos x)(1 − cos x)
= 1 − sin2
φ = cos2
φ =
2
1 − cos2
x
36. cos x(sec x − cos x) = cos x
1
− cos x

=
2
cos x

sin2
x

= 1 − cos2
x
= sin2
x
44.
= 2 csc2
x
1
−
1
=
sec x − 1 − (sec x + 1)
37. sin β tan β + cos β = (sin β)
sin β
+ cos β
cos
β sec x + 1 sec x − 1

(
s
ec x + 1)(sec x
− 1)
=
sec x − 1 − sec x − 1
sin2
β
= +
cos β
cos2
β
cos β
sec2
x − 1
=
−2
sin2
β + cos2
β
=
cos β
tan2
x
1 
= −2 2
=
1 tan x
cos β
= sec β
= −2 cot2
x

45.
cos x
−
cos x
=
cos x(1 − sin x) − cos x(1 + sin x)
1 + sin x 1 − sin x (1 + sin x)(1 − sin x)
=
cos x − sin x cos x − cos x − sin x cos x
(1 + sin x)(1 − sin x)
=
−2sin x cos x
1 − sin2
x
=
−2sin x cos x
cos2
x
=
−2sin x
cos x
= −2 tan x
46.
sin x
1 + cos x
+
sin x
=
1 − cos x
sin x(1 − cos x) + sin x(1 + cos x)
(1 + cos x)(1 − cos x)
=
sin x − sin x cos x + sin x + sin x cos x
(1 + cos x)(1 − cos x)
=
2sin x
1 − cos2
x
=
2sin x
sin2
x
=
2
sin x
= 2 csc x
47.
sec2
x
tan x − =
tan2
x − sec2
x
50.
5
⋅
tan x − sec x
=
5(tan x − sec x)
tan x tan x
=
−1
= −cot x
tan x
2 2
tan x + sec x tan x − sec x tan2
x − sec2
x
5(tan x − sec x)=
−1
= 5(sec x − tan x)
48.
cos x 1 + sin x cos x + (1 + sin x)+ =
y =
1
sin x cot x + cos x
1 + sin x cos x cos x(1 + sin x)
cos2
x + 1 + 2 sin x + sin2
x
51. 1 ( )
2
= 1

cos x
cos x(1 + sin x) = sin x + cos x
=
2 + 2 sin x
2 sin x 
1
cos x(1 + sin x) = (cos x + cos x)
2
2(1+ sin x)=
cos x(1 + sin x)
= cos x
2
=
2
cos x
= 2 sec x
−2π 2π
49.
sin2
y
1 − cos y
−2
1 − cos2
y
=
1 − cos y
(1 + cos y)(1 − cos y)=
1 − cos y

= 1 + cos y


52. y1 = sec x csc x − tan x
1 1 sin x
= −
53. y =
tan x + 1
1
sec x + csc x
cos x sin x cos x sin x
+ 1
1 sin2
x
= − =
cos x
1 1
cos x sin x
1 − sin2
x
cos x sin x
cos x
+
sin x
=
cos x sin x
cos2
x
=
cos x sin x
cos x
=
sin x + cos x
=
cos x
sin x + cos x
sin x cos x
sin x + cos x  sin x cos x
sin x =
= cotx
6

= sin x
cos x sin x + cos x
2
−2π 2π
−2π 2π
−6
54. y1 =
1 1
−2

− cos x = tan x
sin x cos x 5
1 1 1 cos x
− cos x = −
sin x cos x sin x cos x sin x −2π 2π

1 − cos2
x sin2
x sin x
= = = = tan x −5
sin x cos x sin x cos x cos x
55. Let x = 3 cos θ. 57. Let x = 2 sec θ.
9 − x2
=
=
=
9 − (3 cos θ)
2
9 − 9 cos2
θ
9(1 − cos2
θ)
x2
− 4 =
=
=
(2 sec θ)
2
− 4
4(sec2
θ − 1)
4 tan2
θ
= 9 sin2
θ = 3 sin θ = 2 tan θ
56. Let x = 7 sin θ. 58. Let 3x = 5 tan θ.
2 2
49 − x2
= 49 − (7 sin θ)
2 9x + 25 = (3x) + 25
= 49 − 49 sin2
θ
= 49(1 − sin2
θ)
= 49 cos2
θ

= (5 tan θ)
2
+ 25
= 25 tan2
θ + 25
= 25(tan2
θ + 1)
= 7 cos θ = 25 sec2
θ
= 5 sec θ

= ± 1 −
1
59. Let x = 2 sin θ.
4 − x2
= 2
4 − (2 sin θ)
2
= 2
4 − 4 sin2
θ = 2
4(1 − sin2
θ) = 2
4 cos2
θ = 2
2 cos θ = 2
cos θ =
2
2
2
sin θ = 1 − cos2
θ =
2 2
1 − = ±
60. Let x = 2 cos θ.
2  2
61. x = 6 sin θ
16 − 4x2
= 2 2 3 = 36 − x2
16 − 4(2 cos θ)
2
= 2 2 = 36 − (6 sin θ)
2
16 − 16 cos2
θ
16(1 − cos2
θ)
= 2 2
= 2 2
=
=
36(1 − sin2
θ)
36 cos2
θ
16 sin2
θ = 2 2 = 6 cos θ
4 sin θ = ±2 2 cos θ =
3
=
1
sin θ = ±
2
2 sin θ
6 2
= ± 1 − cos2
θ
cos θ =
=
1 − sin2
θ
1 −
1
2


2
2
= ±
3
=
1 4
2
= ±
3
2 2
=
2
62. x = 10 cos θ
5 3 =
5 3 =
5 3 =
5 3 =
100 − x2
100 − (10 cos θ)
2
100(1 − cos2
θ)
100 sin2
θ
5 3 = 10 sin θ
sin θ =
5 3
=
3
cos θ = 10 2

1 − sin2
θ =
2
3
1
1 − =
2 2

63. sin θ = 1 − cos2
θ 67. μW cos θ
μ
= W sin θ
W sin θ
= = tan θ
Let y1 = sin x and y2 = 1 − cos2
x, 0 ≤ x ≤ 2π. W cos θ
y1 = y2 for 0 ≤ x ≤ π.
sec x tan x − sin x =
1
⋅
sin x
− sin x
So, sin θ = 1 − cos2
θ for 0 ≤ θ ≤ π. 68.
cos x cos x
2
y2
0 2π
y1
sin x
= − sin x
cos2
x
sin x − sin x cos2
x
=
cos2
x
64.
−2
cos θ = − 1 − sin2
θ
sin x(1 − cos2
x)=
cos2
x
2
sin x sin x
= 2
Let y1 = cos x and y2 = − 1 − sin2
x, 0 ≤ x ≤ 2π. cos x
2
y1 =
π
y2 for ≤ x ≤
3π
.
= sin x tan x
So, cos θ
2 2
= − 1 − sin2
θ for
π 3π
≤ θ ≤ .
69. True.
sin u
2 2
2
0 2π
tan u =
cos u
cot u =
cos u
sin u
sec u =
1
cos u
65.
−2
sec θ = 1 + tan2
θ
1
csc u =
1
sin u
Let y1 = and y2 =
cos x
π
1 + tan2
x, 0 ≤ x ≤ 2π.
3π
70. False. A cofunction identity can be used to transform a
tangent function so that it can be represented by a
cotangent function.
y1 = y2 for 0 ≤ x < and
2 2
< x ≤ 2π.
π −
71. As x → , tan x → ∞ and cot x → 0.
So, sec θ = 1 + tan2
θ for 0 ≤ θ <
π
2
and
2
+ 1
3π
< θ
2
< 2π. 4
72. As x → π , sin x → 0 and csc x =
sin x
→ −∞.
y2
0 2π
y1
−4
73. cos(−θ) ≠ −cos θ
cos(−θ) = cos θ
The correct identity is
sin θ
=
cos(−θ)
sin θ
cos θ
66. csc θ = 1 + cot2
θ
1
= tan θ
Let y1 = and y2 = s
i
n x

1 + cot2
x, 0 ≤ x ≤ 2π.
74. Let u = a tan θ,
then
y1 = y2 for 0 < x < π.
a2
+ u2
= a2
+ (a tan θ)
2
So, csc θ = 1 + cot2
θ for 0 < θ < π. 2 2 2
= a + a
2
tan θ
0 2π
= a2
(1 + tan2
θ)
= a2
sec2
θ
= a sec θ.
−2

= 1 +
a
= 1 +
b
2
75. Because sin2
θ + cos2
θ = 1, then cos2
θ = 1 − sin2
θ.
cos θ = ± 1 − sin θ
tan θ =
sin θ
=
sin θ
cot θ
cos θ ±
=
cos θ
=
±
sin θ
1 − sin2
θ
1 − sin2
θ
sin θ
sec θ =
1
=
1
csc θ
cos θ
1
=
sin θ
± 1 − sin2
θ
76. To derive sin2
θ + cos2
θ = 1, let sin θ =
a
and cos θ =
b
a2
+ b2
a2
+ b2
.
2 2
a b a b2
So, sin2
θ + cos2
θ =  + = +
a2
+ b2
 a2
+ b2
 a2
+ b2
a2
+ b2
=
a2
+ b2
a2
+ b2
= 1.
To derive 1 + tan2
θ = sec2
θ, let tan θ =
a
and sec θ
b
a2
+ b2
= .
b
So, 1 + tan2
θ
2


b 
a2
= 1 + =
b2
b2
+ a2
b2
2 2
a2
+ b2 a2
+ b2
= =
b2
b


= sec2
θ.
To derive 1 + cot2
θ = csc2
θ, let cot θ =
b
and csc θ
a
a2
+ b2
= .
a
So, 1 + cot2
θ
2


a 
= 1 +
b2
a2
2
a2
+ b2
a2
+ b2
= =
a2 
a2

2
a2
+ b2
=  = csc2
θ.
a


Answers will vary.

1
1 +
sin θ 


 

Section 2.2 Verifying Trigonometric Identities 221
77.
sec θ(1 + tan θ)
sec θ + csc θ

cos θ cos θ 
=
1
+
1
cos θ sin θ
cos θ + sin θ
= cos2
θ
sin θ + cos θ
sin θ cos θ
=
sin θ + cos θ sin θ cos θ
cos2
θ sin θ + cos θ

=
sin θ
cos θ
Section 2.2 Verifying Trigonometric Identities
1. identity
2. conditional equation
3. tan u
16.
cos(π 2) − x
sin(π 2) − x
π 
sin x
= = tan x
cos x
1
4. cot u
17. sin t csc
2
− t = sin t sec t = sin t
cos t
5. sin u
sin t
=
cos t
= tan t
6. cot2
u
7. −csc u
18. sec2
y − cot2 π
2
− y = sec2
y − tan2
y = 1

8. sec u
19.
1
+
1
=
cot x + tan x
9. tan t cot t =
sin t
cos t
⋅
cos t
= 1
sin t
tan x cot x tan x cot x
=
cot x + tan x
1
10.
tan x cot x
cos x
=
1
= sec x
cos x
20.
= tan x + cot x
1
−
1
=
csc x − sin x
11. (1 + sin α)(1 − sin α) = 1 − sin2
α = cos2
α sin x csc x sin x csc x
csc x − sin x
=
12. cos2
β − sin2
β = cos2
β − (1 − cos2
β)
= 2 cos2
β − 1
1
= csc x − sin x
13.
14.
cos2
β − sin2
β
sin2
α − sin4
α
= (1 − sin2
β) − sin2
β
= 1 − 2 sin2
β
= sin2
α(1 − sin2
α)
= (1 − cos2
α)(cos2
α)
= cos2
α − cos4
α
21.
1 + sin θ
cos θ
+
cos θ
=
1 + sin θ
=
=
(1 + sin θ)
2
+ cos2
θ
cos θ(1 + sin θ)
1 + 2 sin θ + sin2
θ + cos2
θ
cos θ(1 + sin θ)
2 + 2 sin θ
cos θ(1 + sin θ)
2(1+ sin θ)
15. tan
π
2
− θ tan θ = cot θ tan θ
=
cos θ(1 + sin θ)


1 
= tan θ
tan θ 
= 1
=
2
cos θ
= 2 sec θ


( )
(
cos θ cot θ cos θ cot θ − (1 − sin θ) 1
22.
1 − sin θ
− 1 =
=
1 − sin θ
cos θ 
cos θ
sin θ
−
1 + sin θ
⋅
1 − sin θ
cos2
θ − sin θ + sin2
θ
sin θ
sin θ
25.
26.
27.
sec y cos y = cos y = 1
cos y 
cot2
y(sec2
y − 1) = cot2
y tan2
y = 1
tan
=
( ) = sin θ tan θ
2
θ sin θ cos θ tan θ
=
sin θ(1 − sin θ) sec θ 1 cos θ
=
1 − sin θ
sin θ(1 − sin θ)
=
1
sin θ
= csc θ
28.
cot3
t
csc t
cot t cot2
t
=
csc t
cot t(csc2
t − 1)=
csc t
cos t
csc2
t − 1
sin t
23.
1 1
+ =
cos x + 1 cos x − 1
=
cos x − 1 + cos x + 1
(cos x + 1)(cos x − 1)
2 cos x
cos2
x − 1
2 cos x
=
1
sin t
=
cos t sin t
csc2
sin t
t − 1)
=
−sin2
x = cos t(csc2
t − 1)
= −2 ⋅
1
⋅
cos x
1 1 + tan2
β
sin x sin x 29.
tan β
+ tan β =
tan β
24.
= −2 csc x cot x
cos x −
cos x
=
cos x(1 − tan x) − cos x
sec2
β
=
tan β
1 − tan x 1 − tan x
=
−cos x tan x
1 − tan x
−cos x(sin x cos x) cos x
= ⋅
1 − (sin x cos x)
=
−sin x cos x
cos x − sin x
sin x cos x
cos x
=
sin x − cos x
30.
sec θ − 1
=
sec θ − 1
⋅
sec θ sec θ(sec θ − 1)= = sec θ
1 − cos θ 1 − (1 sec θ) sec θ sec θ − 1
cot2
t cos2
t sin2
t cos2
t 1 − sin2
t 1
31. = = = 33. sec x − cos x = − cos x
csc t 1 sin t sin t sin t cos x
1 − cos2
x
=

32.
sin x 
cos x + sin x tan x = cos x + sin x 
cos x 
cos2
x + sin2
x
cos x
sin2
x
=
cos x
=
cos x
= sin x ⋅
sin x
=
1
cos x
= sec x
cos x
= sin x tan x

 
34. cot x − tan x =
cos x
−
sin x
sin x cos x
cos2
x − sin2
x
=
sin x cos x
1 − sin2
x − sin2
x
=
sin x cos x
1 − 2 sin2
x
=
sin x cos x
1 1 − 2 sin2
x 
=
cos x sin x
1 1 2 sin2
x
=
cos x sin x
−
sin x
= sec x(csc x − 2 sin x)
cot x cos x sin x cos2
x 1 − sin2
x 1 sin2
x
35. = = = = − = csc x − sin x
36.
sec x
csc(−x)
sec(−x)
1 cos x
1 sin(−x)=
1 cos(−x)
cos(−x)
sin x sin x sin x sin x
=
sin(−x)
37.
=
cos x
−sin x
= −cot x
sin1 2
x cos x − sin5 2
x cos x = sin1 2
x cos x(1 − sin2
x) = sin1 2
x cos x ⋅ cos2
x = cos3
x sin x
38. sec6
x(sec x tan x) − sec4
x(sec x tan x) = sec4
x(sec x tan x)(sec2
x − 1) = sec4
x(sec x tan x) tan2
x = sec5
x tan3
x
39. (1 + sin y)1 + sin(−y) = (1 + sin y)(1 − sin y)
= 1 − sin2
y
41.
1 + sin θ
=
1 − sin θ
1 + sin θ
1 − sin θ
1 + sin θ
⋅
1 + sin θ
40.
= cos2
y
1
+
1
tan x + tan y
=
cot x cot y
⋅
cot x cot y
(1 + sin θ)
2
=
1 − sin2
θ
(1 + sin θ)
2
=1 − tan x tan y
1 −
1
⋅
1 cot x cot y cos2
θ
cot x cot y
1 + sin θ
==
cot y + cot x
cot x cot y − 1 cos θ
42.
cos x − cos y
+
sin x − sin y
=
(cos x − cos y)(cos x + cos y) + (sin x − sin y)(sin x + sin y)
sin x + sin y cos x + cos y (sin x + sin y)(cos x + cos y)
cos2
x − cos2
y + sin2
x − sin2
y
=
(sin x + sin y)(cos x + cos y)
(cos2
x + sin2
x) − (cos2
y + sin2
y)=
(sin x + sin y)(cos x + cos y)
43. = 0

cot(
− x)
≠
cot
x
44. The first line claims that sec(−θ)
= −sec θ
and
The correct substitution is cot(− x) = −cot x. sin(−θ ) = sin θ. The correct substitutions are
1
+ cot(− x) = cot x − cot x = 0
tan x
sec(−θ) = sec θ and sin(−θ ) = −sin θ.

( )( )

( 2 2
)

45. (a) 3
−2π 2π
−1
Identity
(b)
Identity
(c) 1 + cot2
x cos2
x = csc2
x cos2
x =
1
⋅ cos2
x = cot2
x
sin2
x
3
46. (a) (b)
−2π 2π
−1
Identity
Identity
(c) csc x(csc x − sin x) +
sin x − cos x
+ cot x = csc2
x − csc x sin x + 1 −
cos x
+ cot x
sin x sin x
= csc2
x − 1 + 1 − cot x + cot x
= csc2
x
47. (a)
5
y2
y1
−2π 2π
−1
Not an identity
(b)
Not an identity
(c) 2 + cos2
x − 3 cos4
x = (1 − cos2
x)(2 + 3 cos2
x) = sin2
x(2 + 3 cos2
x) ≠ sin2
x(3 + 2 cos2
x)
48. (a)
−π
5
y1 y2
π
(b)
−5
Not an identity
sin4
x sin2
x
Not an identity
(c) tan4
x + tan2
x − 3 = + − 3
cos4
x
1
cos2
x
sin4
x
=
cos2
x cos2
x
+ sin2
x − 3
1 sin4
x + sin2
x cos2
x
= 
cos2
x cos2
x
− 3

1 sin2
x 
= sin x + cos x − 3
cos2
x cos2
x
1 sin2
x 
=
cos2
x cos2
x
⋅ 1 − 3

= sec2
x tan2
x − 3
≠ sec2
x(4 tan2
x − 3)

.
cos2
x
( )
49. (a) 3 50. (a) 3
y1
−2π 2π
−2 2
y2
−3 −5
(b)
Identity
(b)
Not an identity
(c)
Identity
1 + cos x (1 + cos x)(1 − cos x)=
Not an identity
(c)
cot α
is the reciprocal of
csc α + 1
sin x sin x(1 − cos x) csc α + 1 cot α
1 − cos2
x
=
sin x(1 − cos x)
sin2
x
=
sin x(1 − cos x)
sin x
=
51.
They will only be equivalent at isolated points in
their respective domains. So, not an identity.
tan3
x sec2
x − tan3
x = tan3
x(sec2
x − 1)
= tan3
x tan2
x
5
1 − cos x = tan x
2 4
52. (tan2
x + tan4
x) sec2
x =
sin x sin x 1
+ 
cos4
x cos2
x
1 
= sin2
x +
sin4
x 
cos4
x cos2
x
1 sin2
x cos2
x + sin4
x
=
cos4
x cos2
x
1 sin2
x cos2
x + sin2
x 
=
cos4
x cos2
x
1 sin2
x
= 

⋅ 1 = sec4
x ⋅ tan2
x
cos4
x cos2
x 
53. (sin2
x − sin4
x) cos x = sin2
x(1 − sin2
x) cos x
= sin2
x cos2
x cos x
= sin2
x cos3
x
54. sin4
x + cos4
x = sin2
x sin2
x + cos4
x
= (1 − cos2
x)(1 − cos2
x) + cos4
x
= 1 − 2 cos2
x + cos4
x + cos4
x
= 1 − 2 cos2
x + 2 cos4
x
55. sin2
25° + sin2
65° = sin2
25° + cos2
(90° − 65°)
= sin2
25° + cos2
25°
= 1
56. tan2
63° + cot2
16° − sec2
74° − csc2
27° = tan2
63° + cot2
16° − csc2
(90° − 74°) − sec2
(90° − 27°)
= tan2
63° + cot2
16° − csc2
16° − sec2
63°

=
(
t
a
n
2
6
3
°
−
s
e
c
2
6
3
°
)
+
(
c
o
t
2
1
6
°
−
c
s
c
2
1
6
°
)
=
−
1
+
(
−
1
)
=
−
2

θ 15° 30° 45° 60° 75° 90°
s 18.66 8.66 5 2.89 1.34 0
1
57. Let θ = sin−1
x sin θ = x =
x
. 60. Let θ = cos−1 x + 1
cos θ =
x + 1
.
1 2 2
1
x 2
4 − (x + 1)2
θ
1 − x2
θ
x + 1
From the diagram, From the diagram,
tan(sin−1
x) = tan θ =
x
. −1 x + 1 4 − (x + 1)2
1 − x2 tancos
2
= tan θ =
x 1
.
58. Let θ = sin−1
x sin θ = x =
x
.
+
1 cos x
1 61. cos x − csc x cot x = cos x −
sin x sin x
1 
= cos x1 −
sin2
x
x
θ
1 − x2
= cos x(1 − csc2
x)
= −cos x(csc2
x − 1)
= −cos x cot2
x
From the diagram,
cos(sin−1
x) = cos θ
1 − x2
= =
1
1 − x2
.
62. (a)
(b)
h sin(90° −θ)
sin θ
=
h cos θ
= h cot θ
sin θ
59. Let θ = sin−1 x − 1
sin θ =
x − 1
.
4 4
4
x − 1
(c) Maximum: 15°
Minimum: 90°
(d) Noon
θ 63. False. tan x2
= tan(x ⋅ x) and
16 − (x − 1)2
From the diagram,
tansin−1 x − 1
= tan θ
x − 1
= .
tan2
x = (tan x)(tan x), tan x2
64. True. Cosine is an even function,
≠ tan2
x.
π  π
4  16 − (x − 1)
2
cosθ − = cos− − θ
2  
= cos
π
2 
− θ
2


= sin θ.

65. False. For the equation to be an identity, it must be true
for all values of θ in the domain.

2
b
2
b
2 2
2
Section 2.3 Solving Trigonometric Equations 227
66. If sin θ =
a
, sec θ =
c
, and 68. tan θ = sec2
θ − 1
c b
True identity: tan θ = ± sec2
θ − 1
a2
+ b2
= c2
a2
c 
= c2
− b2
, then
tan θ = sec2
θ − 1 is not true for π 2 < θ < π
sec2
θ − 1
− 1
=  or 3π 2 < θ < 2π. So, the equation is not true for
sec2
θ c 


c2
θ
69.
= 3π 4.
1 − cos θ = sin θ
b2
− 1
=
c2 (1 − cos θ) = (sin θ)
2 2
b2 1 − 2 cos θ + cos θ = sin θ
c2
− b2
= b2
c2
1 − 2 cos θ + cos2
θ
2 cos2
θ − 2 cos θ
= 1 − cos2
θ
= 0
b2
c2
− b2
b2
= ⋅
b2
c2
c2
− b2
2 cos θ(cos θ − 1) = 0
The equation is not an identity because it is only true
when cos θ = 0 or cos θ = 1. So, one angle for which
the equation is not true is −
π
.
=
c2
a2 70.
=
c2
1 + tan θ
(1 + tan θ)
2
2
= sec θ
= (sec θ)
2
a 2 2
=  1 + 2 tan θ + tan θ = sec θ
c 
= sin2
θ.
1 + 2 tan θ + tan2
θ
2 tan θ
= 1 + tan2
θ
= 0
67. Because sin2
θ = 1 − cos2
θ, then tan θ = 0
sin θ = ± 1 − cos2
θ ; sin θ ≠ 1 − cos2
θ if θ This equation is not an identity because it is only true
lies in Quadrant III or IV.
when tan θ = 0. So, one angle for which the equation
One such angle is θ =
7π
.
4
is not true is
π
.
6
Section 2.3 Solving Trigonometric Equations
1. isolate 6. sec x − 2 = 0
2. general
3. quadratic
(a) x =
π
3
sec
π
− 2 =
1
− 2
4. extraneous
5.
ta
n
x −

3 = 0
3
cos(π
3)
=
1
−
2
=
2
−
2
=
0
1
2
(a) x =
π
3
tan
π
− 3 = 3 − 3 = 0
(b) x =
5π
3
sec
5π
− 2 =
1
− 2
(b)
3
x =
4π
3
3 cos(5π 3)
=
1
− 2 = 2 − 2 = 0
1 2
tan
4π
− 3 =
3
3 − 3 = 0


=
2 cos2 2
2
2 cos2 2
2  = −
7. 3 tan2
2x − 1 = 0 10. csc4
x − 4 csc2
x = 0
(a) x =
π
12
2
3tan 2
π 
− 1 = 3 tan2 π
− 1
(a) x =
π
6
csc4 π
− 4 csc2 π 1 4
= −
12 6 4 2
 2
1 
3 − 1
6 6 sin (π 6)
1 4= −
sin (π 6)
3  (1 2)
4
(1 2)
2
(b)
= 0
x =
5π
12
2
(b) x =
5π
6
= 16 − 16 = 0
3tan 2
5π

− 1 = 3 tan2 5π
− 1 csc4 5π
4 csc
5π 1 4

12 6
− = 4
− 2

2
1 
= 3− − 1
6 6 sin (5π 6)
1 4
= −
sin (5π 6)
3  (1 2)
4
(1 2)
2
= 0
8. 2 cos2
4x − 1 = 0
11. 3 csc x − 2 = 0
= 16 − 16 = 0
(a) x =
π
16
π π
4 − 1 = 2 cos − 1
3 csc x = 2
csc x =
2
3
16 4
2

x =
π
+ 2nπ
3
= 2 2
− 1
2
(b) x =
3π

1 
= 2 − 1 = 1 − 1 = 0

12. tan x +
or x =
2π
3
3 = 0
+ 2nπ
16
3π 3π
4 − 1 = 2 cos − 1
tan x = − 3
x =
2π
+ nπ
16  4
2
2 
= 2− − 1
3
13. cos x + 1 = −cos x
2

2 cos x + 1 = 0

=
1
− 1 = 0
2
cos x
1
2
x =
2π
+ 2nπ or x =
4π
+ 2nπ
9. 2 sin2
x − sin x − 1 = 0 3 3

2
(a)
x =
π
2
2 sin2 π
− sin
π
− 1 = 2(1)2
− 1 − 1
14. 3 sin x + 1 = sin x
2 sin x + 1 = 0
1
2 2 sin x = −
= 0 7π
(b) x =
7π
6
2 sin2 7π
− sin
7π 1
2
− 1 = 2− 
1
− − − 1
x = + 2nπ or
6
x =
11π
+ 2nπ
6
6 6  2 2
=
1
+
1
− 1
2 2
= 0

15. 3 sec2
x − 4 = 0 20. (2 sin2
x − 1)(tan2
x − 3) = 0
sec2
x =
4
3
2 sin2
x − 1 = 0 or tan2
x = 3
sec x = ±
2
3
sin2
x =
1
2
tan x = ± 3
x =
π
6
+ nπ
sin x = ±
1
2
x =
π
3
+ nπ
or x =
5π
+ nπ sin x = ±
2
x =
2π
+ nπ
16.
6
3 cot2
x − 1 = 0
cot2
x =
1
x =
π
4
x =
3π
2 3
+ 2nπ
+ 2nπ
3
cot x = ±
1
3
4
x =
5π
4
x =
7π
+ 2nπ
+ 2nπ
x =
π
3
+ nπ 4
or x =
2π
3
+ nπ 21. cos3
x − cos x = 0
cos x(cos2
x − 1) = 0
17. 4 cos2
x − 1 = 0
cos x = 0 or cos2
x − 1 = 0
cos2
x =
1
4
cos x
1
x =
π
+ nπ
2
cos x = ±1
x = nπ
= ±
2 Both of these answers can be represented as x =
nπ
.
x =
π
+ nπ or x =
2π 2
+ nπ
18.
3 3
2 − 4 sin2
x = 0
sin2
x =
1
2
22. sec2
x − 1 = 0
sec2
x = 1
sec x = ±1
x = nπ
sin x = ±
1
2
= ±
2
2 23. 3 tan3
x = tan x
3
x =
π
+ 2nπ
3 tan x − tan x = 0
4
x =
3π
+ 2nπ
tan x(3 tan2
x − 1) = 0
4
x =
5π
4
x =
7π
+ 2nπ
+ 2nπ
tan x = 0
x = nπ
or 3 tan2
x − 1 = 0
tan x = ±
x =
π
3
3
+ nπ,
5π
+ nπ

4
These answers can be represented as x =
π
+
nπ
. 24.
6 6
sec x csc x = 2 csc x
19. sin x(sin x + 1) = 0
4 2
sec x csc x − 2 csc x = 0
csc x(sec x − 2) = 0
sin x = 0 or sin x = −1 csc x = 0 or sec x − 2 = 0
x = nπ x =
3π
2
+ 2nπ No solution sec x = 2
x =
π
+ 2nπ,
5π
+ 2nπ
3 3


= −
25. 2 cos2
x + cos x − 1 = 0
(2 cos x − 1)(cos x + 1) = 0
2 cos x − 1 = 0 or cos x + 1 = 0
cos x =
1 cos x = −1
2
x =
π
+ 2nπ ,
5π
+ 2nπ
x = π + 2nπ
3 3
26. 2 sin2
x + 3 sin x + 1 = 0
(2 sin x + 1)(sin x + 1) = 0
2 sin x + 1 = 0 or sin x + 1 = 0
sin x
1
2
sin x = −1
x =
3π
+ 2nπ
x =
7π
+ 2nπ ,
11π
+ 2nπ 2
6 6
27. sec2
x − sec x = 2
sec2
x − sec x − 2 = 0
(sec x − 2)(sec x + 1) = 0
sec x − 2 = 0
sec x = 2
or sec x + 1 = 0
sec x = −1
x =
π
+ 2nπ,
5π
+ 2nπ
x = π + 2nπ
3 3
28. csc2
x + csc x = 2
csc2
x + csc x − 2 = 0
(csc x + 2)(csc x − 1) = 0
csc x + 2 = 0
csc x = −2
or csc x − 1 = 0
csc x = 1
x =
7π
+ 2nπ,
11π
+ 2nπ x =
π
+ 2nπ
6 6 2
29. sin x − 2 = cos x − 2
sin x = cos x
30. cos x + sin x tan x = 2
cos x + sin x
sin x
= 2
sin x
= 1
cos x
cos x
cos2
x + sin2
x
tan x = 1
x = tan−1
1
x =
π
,
5π
4 4
cos x
= 2
1
= 2
cos x
1
cos x =
2
x =
π
,
5π
3 3


31. 2 sin2
x = 2 + cos x
2 − 2 cos2
x = 2 + cos x
2 cos2
x + cos x = 0
36. 3 sec x − 4 cos x = 0
3
− 4 cos x = 0
cos x
cos x(2 cos x + 1) = 0
3 − 4 cos2
x
= 0
cos x
cos x = 0 or 2 cos x + 1 = 0
3 − 4 cos2
x = 0
x =
π
,
3π 2 cos x = −1
3
2 2 1
cos x = −
2
cos2
x =
4
3
32. tan2
x = sec x − 1
sec2
x − 1 = sec x − 1
x =
2π
,
4π
3 3
37.
cos x = ±
2
x =
π
,
5π
,
7π
,
11π
6 6 6 6
csc x + cot x = 1
sec2
x − sec x = 0 (csc x + cot x)
2
= 12
33.
sec x(sec x − 1) = 0
sec x = 0 or sec x − 1 = 0
No Solutions sec x = 1
x = 0
sin2
x = 3 cos2
x
csc2
x + 2 csc x cot x + cot2
x = 1
cot2
x + 1 + 2 csc x cot x + cot2
x = 1
2 cot2
x + 2 csc x cot x = 0
2 cot x(cot x + csc x) = 0
2 cot x = 0 or cot x + csc x = 0
x
π
,
3π cos x 1
sin2
x − 3 cos2
x = 0 = = −
2 2 sin x sin x
sin2
x − 3(1 − sin2
x) = 0
4 sin2
x = 3
sin x = ±
3
3π

2
is extraneous.

cos x = −1
x = π
(π is extraneous.)
2
x =
π
,
2π
,
4π
,
5π
3 3 3 3
34. 2 sec2
x + tan2
x − 3 = 0
38.
x = π 2 is the only solution.
sec x + tan x = 1
1 sin x
+ = 1
cos x cos x
2(tan2
x + 1) + tan2
x − 3 = 0
1 + sin x = cos x
3 tan2
x − 1 = 0
(1 + sin x)
2
= cos2
x
tan x = ±
3
3
1 + 2 sin x + sin2
x = cos2
x
1 + 2 sin x + sin2
x = 1 − sin2
x
x =
π
,
5π
,
7π
,
11π
6 6 6 6 2 sin2
x + 2 sin x = 0
35. 2 sin x + csc x = 0
2 sin x +
1
= 0
2 sin x(sin x + 1) = 0
sin x = 0 or sin x + 1 = 0

.
sin x
2 sin2
x + 1 = 0
sin2
x
1
No solution
x = 0, π
(π is extraneous.)
sin x = −1
x =
3π
2
= −
2
x = 0 is the only solution.
3π

2
is extraneous 

2
2
39. 2 cos 2x − 1 = 0
45. 3 tan
x
− 3 = 0
cos 2x =
1
2
2
tan
x
=
3
2x =
π
+ 2nπ or 2x =
5π 2 3
+ 2nπ
3 3 x
=
π
+ nπ x =
π
+ 2nπ
x =
π
+ nπ x =
5π
+ nπ
2 6 3
6 6
x
46. tan + 3 = 0
40. 2 sin 2x + 3 = 0
2
x
sin 2x = −
3
2
tan
2
x
= − 3
=
2π
+ nπ x =
4π
+ 2nπ
2x =
4π
+ 2nπ or 2x =
5π
+ 2nπ 2 3 3
3 3
x =
2π
+ nπ x =
5π
+ nπ 47. y = sin
π x
+ 1
3 6 2
π x
+ =41. tan 3x − 1 = 0
tan 3x = 1
sin 1 0

π x
3x =
π
+ nπ
sin = −1
4
x =
π
+
nπ
π x
2
=
3π
2
+ 2nπ
12 3
42. sec 4x − 2 = 0
sec 4x = 2
cos 4x =
1
2
48.
x = 3 + 4n
For −2 < x < 4, the intercepts are −1 and 3.
y = sin π x + cos π x
sin π x + cos π x = 0
sin π x = −cos π x
4x =
π
+ 2nπ or 4x =
5π
+ 2nπ π
3 3 π x = − + nπ
4
x =
π
+
nπ
x =
5π
+
nπ
1
12 2 12 2 x = − + n
4
43. 2 cos
x
= 2 = 0 For 1 x 3, the intercepts are −
1
,
3
,
7
,
11
2
cos
x
=
2
− < < .
4 4 4 4
2 2 49. 5 sin x + 2 = 0
8
x
=
π
+ 2nπ or
x
=
7π
+ 2nπ

2 4 2 4
x =
π
+ 4nπ x =
7π
+ 4nπ 0 2π
2 2
44. 2 sin
x
=
2
3 = 0
−5
x ≈ 3.553 and x ≈ 5.872
sin
x
= −
3 50. 2 tan x + 7 = 0
2 2 15
x
=
4π
+ 2nπ or
x 5π
= + 2nπ
2 3 2 3
x =
8π
+ 4nπ x =
10π
+ 4nπ
0 2π
3 3 −5
x ≈ 1.849 and x ≈ 4.991

51. sin x − 3 cos x = 0
5
55. sec2
x − 3 = 0
5
0 2π
0 2π
−5
x ≈ 1.249 and x ≈ 4.391
52. sin x + 4 cos x = 0
5
56.
−4
x ≈ 0.955, x ≈ 2.186, x ≈ 4.097 and x ≈ 5.328
csc2
x − 5 = 0
5
0 2π
0 2π
−5
x ≈ 1.816 and x ≈ 4.957
−5
x ≈ 0.464, x ≈ 2.678, x = 3.605 and x ≈ 5.820
53. cos x = x
4 57. 2 tan2
x = 15
6
0 2π
0 2π
−8
x ≈ 0.739
54. tan x = csc x
−18
x ≈ 1.221, x ≈ 1.921, x ≈ 4.362 and x ≈ 5.062
10
58. 6 sin2
x = 5
6
0 2π
0 2π
−10
x ≈ 0.905 and x ≈ 5.379
−18
x ≈ 1.150, x ≈ 1.991, x ≈ 4.292 and x ≈ 5.133
59. tan2
x + tan x − 12 = 0
(tan x + 4)(tan x − 3) = 0
tan x + 4 = 0 or tan x − 3 = 0
tan x = −4 tan x = 3
x = arctan(−4) + nπ x = arctan 3 + nπ
60. tan2
x − tan x − 2 = 0
(tan x + 1)(tan x − 2) = 0
tan x + 1 = 0 or tan x − 2 = 0
x =
3π
4
+ nπ x = arctan 2 + nπ

3 3
61. sec2
x − 6 tan x = −4
1 + tan2
x − 6 tan x + 4 = 0
tan2
x − 6 tan x + 5 = 0
(tan x − 1)(tan x − 5) = 0
tan x − 1 = 0 tan x − 5 = 0
tan x = 1 tan x = 5
x =
π
4
+ nπ x = arctan 5 + nπ
62. sec2
x + tan x − 3 = 0
1 + tan2
x + tan x − 3 = 0
tan2
x + tan x − 2 = 0
(tan x + 2)(tan x − 1) = 0
tan x + 2 = 0 tan x − 1 = 0
x = arctan(−2) + nπ x = arctan(1) + nπ
63.
≈ −1.1071 + nπ
2 sin2
x + 5 cos x = 4
2(1 − cos2
x) + 5 cos x − 4 = 0
−2 cos2
x + 5 cos x − 2 = 0
−(2 cos x − 1)(cos x − 2) = 0
=
π
+ nπ
4
2 cos x − 1 = 0 or cos x − 2 = 0
cos x =
1
2
x =
π
+ 2nπ ,
5π
+ 2nπ
cos x = 2
No solution
3 3
64. 2 cos2
x + 7 sin x = 5
2(1 − sin2
x) + 7 sin x − 5 = 0
−2 sin2
x + 7 sin x −3 = 0
−(2 sin x − 1)(sin x − 3) = 0
2 sin x − 1 = 0 or sin x − 3 = 0
sin x =
1
2
sin x = 3
x =
π
+ 2nπ,
5π
+ 2nπ No solution
6 6
65. cot2
x − 9 = 0
cot2
x = 9
1
= tan2
x
9
±
1
= tan x
3
x = arctan 1
+ nπ, arctan(− 1
) + nπ

5 5
=
66. cot2
x − 6 cot x + 5 = 0
(cot x − 5)(cot x − 1) = 0
cot x − 5 = 0 or cot x − 1 = 0
cot x = 5 cot x = 1
1
= tan x
5
1 = tan x
x = arctan
1
+ nπ x =
π
+ nπ
5 4
67. sec2
x − 4 sec x = 0
sec x(sec x − 4) = 0
sec x = 0 sec x − 4 = 0
No solution sec x = 4
1
= cos x
4
x = arccos
1
+ 2nπ , −arccos
1
+ 2nπ
4 4
68. sec2
x + 2 sec x − 8 = 0
(sec x + 4)(sec x − 2) = 0
sec x + 4 = 0 or sec x − 2 = 0
sec x = −4 sec x = 2
−
1
= cos x
1
= cos x
4 2
x = arccos−
1
+ 2nπ, −arccos−
1
+ 2nπ x =
π
+ 2nπ,
5π
+ 2nπ
4 4 3 3
69. csc2
x + 3 csc x − 4 = 0
(csc x + 4)(csc x − 1) = 0
csc x + 4 = 0 or csc x − 1 = 0
csc x = −4 csc x = 1
−
1
= sin x
4
1 = sin x
x = arcsin
1
+ 2nπ, arcsin−
1
+ 2nπ x =
π
+ 2nπ
4 4 2
70. csc2
x − 5 csc x = 0
csc x(csc x − 5) = 0
csc x = 0 or csc x − 5 = 0
No solution csc x = 5
1 sin x5
x = arcsin(1
) + 2nπ, arcsin(− 1
) + 2nπ

3

71. 12 sin2
x − 13 sin x + 3 = 0
−(−13) ± (−13)
2
− 4(12)(3)
30
13 ± 5
sin x = =
2(12) 24
0 2π
sin x =
1
or sin x =
3
−10
3 4
x ≈ 0.3398, 2.8018 x ≈ 0.8481, 2.2935
The x-intercepts occur at x ≈ 0.3398,
x ≈ 0.8481, x ≈ 2.2935, and x ≈ 2.8018.
72. 3 tan2
x + 4 tan x − 4 = 0
−4 ± 42
− 4(3)(−4) −4 ± 64 2
tan x = = = −2,
tan x = −2 tan x =
2(3) 6 3
2
3 50
x = arctan(−2) + nπ
≈ −1.1071 + nπ
x = arctan
2
+ nπ

≈ 0.5880 + nπ 0 2
The values of x in [0, 2π) are 0.5880, 3.7296, 2.0344, 5.1760. −10
73. tan2
x + 3 tan x + 1 = 0
−3 ± 32
− 4(1)(1) −3 ± 5
tan x = = 10
2(1) 2
tan x =
−3 − 5
or tan x =
−3 + 5
0 2π
2 2
x ≈ 1.9357, 5.0773 x ≈ 2.7767, 5.9183 −5
The x-intercepts occur at x ≈ 1.9357, x ≈ 2.7767,
x ≈ 5.0773, and x ≈ 5.9183.
74. 4 cos2
x − 4 cos x − 1 = 0
4 ± (−4)
2
− 4(4)(−1) 4 ± 32 1 ± 2
cos x = = =
cos x =
1 − 2
2(4) 8 2
cos x =
1 + 2
7
2 2
−1 2
x = arccos  No solution
2
 0 2π

≈ 1.7794
1 + 2 −3
> 1
2 
−1 − 2 
Solutions in [0, 2π) are arccos and 2π − arccos
1 2
: 1.7794, 4.5038.

−

−

−

75. 3 tan2
x + 5 tan x − 4 = 0, 

3
π
,
π 
2 2
77. 4 cos2
x − 2 sin x + 1 = 0, 

6
π
,
π 
2 2
−π π
2 2
−p p
2 2
76.
−7
x ≈ −1.154, 0.534
cos2
x − 2 cos x − 1 = 0, [0, π]
3
78.
−2
x ≈ 1.110
2 sec2
x + tan x − 6 = 0, 

π
,
π 
2 2
4
0 π
−3
x ≈ 1.998
−π π
2 2
−6
x ≈ −1.035, 0.870
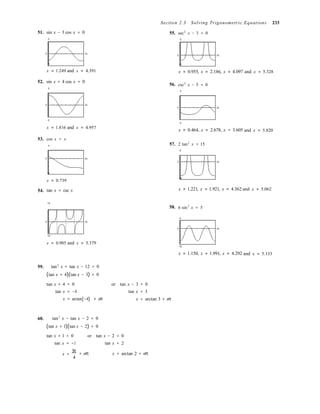
79. (a) f (x) = sin2
x + cos x
2
(b) 2 sin x cos x − sin x = 0
sin x(2 cos x − 1) = 0
0 2π
sin x = 0 or 2 cos x − 1 = 0
x = 0, π
−2 ≈ 0, 3.1416
cos x =
1
2
Maximum: (1.0472, 1.25)
Maximum: (5.2360, 1.25)
Minimum: (0, 1)
Minimum: (3.1416, −1)
x =
π
,
5π
3 3
≈ 1.0472, 5.2360
80. (a) f (x) = cos2
x − sin x
2
(b) −2 sin x cos x − cos x = 0
−cos x(2 sin x + 1) = 0
−cos x = 0 2 sin x + 1 = 0
0 2π
−2
cos x = 0 sin x = −
1
2
x =
π
,
3π
x =
7π
,
11π
Maximum: (3.6652, 1.25) 2 2 6 6
81. (a)
Maximum: (5.7596, 1.25)
Minimum: (1.5708, −1)
Minimum: (4.7124, 1)
f (x) = sin x + cos x
3
≈ 1.5708, 4.7124
(b) cos x − sin x = 0
cos x = sin x
≈ 3.6652, 5.7596
0 2π
1 =
sin x
cos x

−3
Maximum: (0.7854, 1.4142)
Minimum: (3.9270, −1.4142)
tan x = 1
x =
π
,
5π
4 4
≈ 0.7854, 3.9270

2
+=
82. (a) f (x) = 2 sin x + cos 2x
3
(b) 2 cos x − 4 sin x cos x = 0
2 cos x(1 − 2 sin x) = 0
2 cos x = 0 1 − 2 sin x = 0
0 2π
x =
π
,
3π
sin x =
1
2 2 2
−3
Maximum: (0.5236, 1.5)
Maximum: (2.6180, 1.5)
Minimum: (1.5708, 1.0)
Minimum: (4.7124, −3.0)
≈ 1.5708, 4.7124 x =
π
,
5π
6 6
≈ 0.5236, 2.6180
83. (a) f (x) = sin x cos x
2
84. (a) f (x) = sec x + tan x − x
6
0 2π 0 2π
−2
Maximum: (0.7854, 0.5)
Maximum: (3.9270, 0.5)
Minimum: (2.3562, −0.5) (b)
−8
Maximum: (3.1416, −4.1416)
Minimum: (0, 1)
sec x tan x + sec2
x − 1 = 0
Minimum: (5.4978, −0.5) 1
⋅
sin x
+
1
− 1 = 0
(b) −sin2
x + cos2
x = 0 cos x cos x cos x
−sin2
x + 1 − sin2
x = 0
−2 sin2
x + 1 = 0
sin x + 1
− 1 = 0
cos2
x
sin x + 1 cos2
x
− = 0
sin2
x =
1 cos2
x cos2
x
2 sin x + 1 − cos2
x
2
= 0
sin x = ±
1
= ±
2 cos x
2 2 sin x + sin2
x
= 0
x =
π
,
3π
,
5π
,
7π
4 4 4 4
≈ 0.7854, 2.3562, 3.9270, 5.4978
cos2
x
sin x + sin2
x = 0
sin x(1 + sin x) = 0
sin x = 0 or 1 + sin x = 0
x = 0, π
≈ 0, 3.1416
sin x = −1
x =
3π
2
3π
is undefined in original function. So, it is not
2
a solution.
85. The graphs of y1 = 2 sin x and y2
equation 2 sin x = 3x + 1.
= 3x + 1 appear to have one point of intersection. This implies there is one solution to the
86. The graphs of y1 = 2 sin x and y2
1
x 1 appear to have three points of intersection. This implies there are three solutions2

+to the equation 2 sin x =
1 x 1.2

x
32
32
Monthlysales
(inthousandsofdollars)
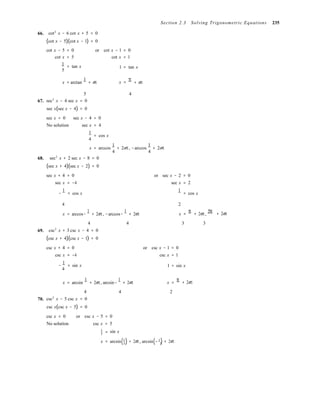
87. f (x) =
sin x 90. Graph the following equations. 4
x y1 = 1.56t −1 2
cos1.9t
0 10
(a) Domain: all real numbers except x = 0. y2 = 1
(b) The graph has y-axis symmetry.
(c) As x → 0, f (x) → 1.
y3 = −1
−4
(d)
sin x
x
= 0 has four solutions in the interval [−8, 8].
The rightmost point of intersection is at approximately
(1.91, −1).
The displacement does not exceed one foot from
sin x
1
= 0

equilibrium after t ≈ 1.91 seconds.
πt
sin x = 0
x = −2π, −π, π, 2π
91. Graph y1 = 58.3 + 32 cos 
6
y2 = 75.
88. f (x) = cos
1
x
(a) Domain: all real numbers x except x = 0.
(b) The graph has y-axis symmetry and a horizontal
asymptote at y = 1.
(c) As x → 0, f (x) oscillates between −1 and 1.
Left point of intersection: (1.95, 75)
Right point of intersection: (10.05, 75)
So, sales exceed 7500 in January, November,
and December.
S
(d) There are infinitely many solutions in the interval
2
100
75
[−1, 1]. They occur at x =
(2n + 1)π
any integer.
where n is 50
25
x
89.
(e) The greatest solution appears to occur at
x ≈ 0.6366.
y =
1
(cos 8t − 3 sin 8t) 92.
2 4 6 8 10 12
Month (1 ↔ January)
Range = 300 feet
12
v0 = 100 feet per second
1
(cos 8t − 3 sin 8t) = 0
12 r = 1
v0
2
sin 2θ
cos 8t = 3 sin 8t
1
= tan 8t
3
8t ≈ 0.32175 + nπ
t ≈ 0.04 +
nπ
8
1
(100)
2
sin 2θ
sin 2θ
2θ
θ
or
= 300
= 0.96
= arcsin(0.96) ≈ 73.74°
≈ 36.9°
In the interval 0 ≤ t ≤ 1, t ≈ 0.04, 0.43, and 0.83. 2θ = 180° − arcsin(0.96) ≈ 106.26°
θ ≈ 53.1°

0
16 2 
16 2 
16 2 
6
1 1
6 6 
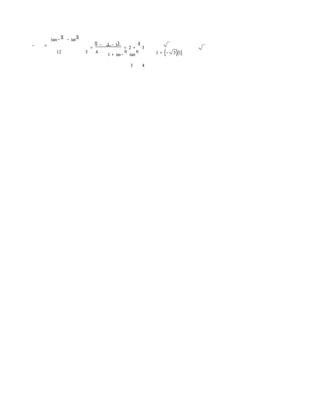
93. (a) and (c)
100
94. h(t) = 53 + 50 sin
π
t −
π 
(a) h(t) = 53 when 50 sin
π
t −
π
= 0.
1 12
0
π
t −
π
= 0 or
π
t −
π
= π
The model fits the data well.
16 2 16 2
π π π 3π
(b) C = a cos(bt − c) + d t = t =
16 2 16 2
a =
1
[high − low] =
1
[84.1 − 31.0] = 26.55
t = 8 t = 24
2 2
p = 2[high time − low time] = 2[7 − 1] = 12
A person on the Ferris wheel will be 53 feet
above ground at 8 seconds and at 24 seconds
b =
2π
p
=
2π
=
π
12 6
(b) The person will be at the top of the Ferris wheel
when
The maximum occurs at 7, so the left end point is sin
π
t −
π
= 1
c
= 7 c = 7
π
=
7π

b 6 π
t −
π
=
π
16 2 2
d = [high + low] = [93.6 + 62.3] = 57.55
2 2
π
16
t = π
C = 26.55 cos
π
t −
7π
+ 57.55

(d) The constant term, d, gives the average maximum
t = 16.
The first time this occurs is after 16 seconds.
2π
temperature. The period of this function is
π 16
= 32.
95.
The average maximum temperature in Chicago is
57.55°F.
(e) The average maximum temperature is above 72°F
from June through September. The average
maximum temperature is below 70°F from October
through May.
A = 2x cos x, 0 < x <
π
2
During 160 seconds, 5 cycles will take place and
the person will be at the top of the ride 5 times,
spaced 32 seconds apart. The times are: 16 seconds,
48 seconds, 80 seconds, 112 seconds, and
144 seconds.
(a) 2
π
2
−2
(b)
The maximum area of A ≈ 1.12 occurs when x ≈ 0.86.
A ≥ 1 for 0.6 < x < 1.1
96. f (x) = 3 sin(0.6x − 2)

(a) Zero: sin(0.6x − 2) = 0 (b) g(x) =
0.6x − 2 = 0
0.6x = 2
x =
2
=
10
4
0
−0.45x2
+ 5.52x − 13.70
6
0.6 3 f
g
−4
For 3.5 ≤ x ≤ 6 the approximation appears to be good.

=
= −

=
(c) −0.45x2
+ 5.52x − 13.70 = 0
−5.52 ± (5.52)
2
− 4(−0.45)(−13.70)
x =
x ≈ 3.46, 8.81
2(−0.45)
The zero of g on [0, 6] is 3.46. The zero is close to the zero
10
3
≈ 3.33 of f.
97. f (x) = tan
π x
4
Because tan π 4 = 1, x = 1 is the smallest nonnegative
fixed point.
100. False.
sin x = 3.4 has no solution because 3.4 is outside the
range of sine.
98. Graph y = cos x and y = x on the same set of axes.
101. cot x cos2
x = 2 cot x
cos2
x = 2
Their point of intersection gives the value of c such that
f (c) = c cos c = c.
2 (0.739, 0.739)
−3 3
−2
c ≈ 0.739
cos x = ± 2
No solution
Because you solved this problem by first dividing by
cot x, you do not get the same solution as Example 3.
When solving equations, you do not want to divide each
side by a variable expression that will cancel out because
you may accidentally remove one of the solutions.
102. The equation 2 cos x − 1 = 0 is equivalent to
99. True. The period of 2 sin 4t − 1 is
π
and the period of
cos x = 1
. So, the points of intersection of y cos x2
2 and y 1
2
represent the solutions of the equation
2 sin t − 1 is 2π. 2 cos x − 1 = 0. In the interval (−2π , 2π ) the solutions
In the interval [0, 2π) the first equation has four cycles
whereas the second equation has only one cycle, so the
first equation has four times the x-intercepts (solutions)
as the second equation.
of the equation are x
5π
, −
π
,
π
, and
3 3 3
5π
.
3
103. (a) 3
0 2π
−2
The graphs intersect when x =
π
2
and x = π.
(b) 3
0 2π
−2
The x-intercepts are
π
, 0 and (π, 0).
2


(c) Both methods produce the same x-values. Answers will vary on which method is preferred.

4 6 4 6
Section 2.4 Sum and Difference Formulas
1. sin u cos v − cos u sin v π π  π π π π
7. (a) cos + = cos cos − sin sin
2. cos u cos v − sin u sin v
3.
tan u + tan v
1 − tan u tan v
4 3  4 3 4 3
2 1 2 3
= ⋅ − ⋅
2 2 2 2
2 − 6
=
4
4. sin u cos v + cos u sin v
(b) cos
π
+ cos
π
=
2
+
1
=
2 + 1
5. cos u cos v + sin u sin v 4 3 2 2 2
7π π  5π π 1
6.
tan u − tan v 8. (a) sin
6
−
3
= sin
6
= sin =
6 2
1 + tan u tan v
(b) sin
7π
− sin
π
= −
1
−
3
=
−1 − 3
9. (a) sin(135° − 30°) = sin 135° cos 30° − cos 135° sin 30°
6 3 2 2 2
2  3  2 1 6 + 2
= − − =
2 2  2 2 4
(b) sin 135° − cos 30° =
2
−
3
=
2 − 3
10. (a)
2 2 2
cos(120° + 45°) = cos 120° cos 45° − sin 120° sin 45°
1 2  3  2 − 2 − 6
= − − =
2 2  2 2 4
(b) cos 120° + cos 45° = −
1
+
2
=
−1 + 2
11. sin
11π = sin
3π
+
π 
2 2 2
tan
11π = tan
3π
+
π

12 

4
= sin
3π
cos
π
+ cos
3π
sin
π
tan
3π
+ tan
π
4 6 4 6 = 4 6
2 3  2 1 1 − tan
3π
tan
π
= ⋅ + − 4 6
2 2  2 2
−1 +
3
co
s
11π

(
4 6
(
2
=
4
= cos
3π
3 − 1)
+
π 
=
3
1
−
(
−
1
)
3
3

12  =
−3 + 3
⋅
3 − 3
= cos
3π
cos
π
− sin
3π
sin
π 3 + 3 3 − 3
4 6 4 6
=
−12 + 6 3
= −2 + 3
2 3 2 1 2
= − ⋅ − ⋅ = − 3 + 1)
6
2 2 2 2 4

4 6
3 4
(
( 
3 4
(
4 6
3 4
)
)
)
Section 2.4 Sum and Difference Formulas 243
12.
7π
=
π
+
π
13. sin
17π
= sin
9π 5π 
−
12 3 4

12
sin
7π
= sin
π
+
π 
= sin
9π
cos
5π
− cos
9π
sin
5π

12 
= sin
π
cos
π
+ sin
π
cos
π
4 6 4 6
2 3 2 1
= − −
3 4 4 3
3 2 2 1
2 2  2 2
= ⋅ + ⋅
2 2 2 2 = −
2
3 + 1
4
=
2
3 + 1
4 cos
17π
12
= cos
9π
4
5π 
−
6
cos
7π
= cos
π
+
π 

= cos
9π
cos
5π
+ sin
9π
sin
5π

12  4 6 4 6
= cos
π
cos
π
− sin
π
sin
π 2 3  2 1
3 4 3 4 =
2
−
2
+
2 2
=
1
⋅
2
−
3
⋅
2

2
2 2 2 2 =
4
(1 − 3)
2
=
4
1 − 3
tan
17π
= tan
9π
−
5π
tan
7π
= tan
π
+
π 

12

12 
tan(9π 4) − tan(5π 6)=
1 + tan(9π 4) tan(5π 6)
tan
π
+ tan
π
= 3 4 1 − (− 3 3)
1 − tan
π
tan
π
3 4
=
1 + (− 3 3)
3 + 1
= =
3 + 3
⋅
3 + 3
1 − 3 3 − 3 3 + 3
= −2 − 3
=
12 + 6 3
6
= 2 + 3
14. −
π
=
π
−
π
12 6 4
sin−
π
= sin
π
−
π 
cos−
π
= cos
π
−
π 
tan−
π
= tan
π
−
π
12 6 4

12 6 4

12 6 4
 

( () )
= sin
π
cos
π − sin
π
cos
π
= cos
π
cos
π
+ sin
π
sin
π
tan
π
− tan
π
6 4 4 6
1 2 2 3
= ⋅ − ⋅
2 2 2 2
2
= 1 − 3
4
6 4 6 4
3 2 1 2
= ⋅ + ⋅
2 2 2 2
=
2
3 + 1
4
= 6 4
1 + tan
π
tan
π
6 4
3
− 1
= 3
1 +
3
3
= −2 + 3

(
(
(
(
(
(
(
)
)
)
)
)
15. sin 105° = sin(60° + 45°)
= sin 60° cos 45° + cos 60° sin 45°
3 2 1 2
= ⋅ + ⋅
2 2 2 2
17. sin(−195°) = sin(30° − 225°)
= sin 30° cos 225° − cos 30° sin 225°
= sin 30°(−cos 45°) − cos 30°(−sin 45°)
=
1
−
2
−
3
−
2 
2 2 2 2
=
2
3 + 1)
4
cos 105° = cos(60° + 45°)
= −
2
1 − 3
4
= cos 60° cos 45° − sin 60° sin 45°
1 2 3 2
=
2
4
3 − 1)
= ⋅ − ⋅
2 2 2 2
2
= 1 − 3
4
cos(−195°) = cos(30° − 225°)
= cos 30° cos 225° + sin 30° sin 225°
= cos 30°(−cos 45°) + sin 30°(−45°)
tan 105° = tan(60° + 45°) 3 2 1 2 
= − + −
tan 60° +tan 45°
=
2 2  2 2
1 − tan 60° tan 45°
= −
2
3 + 1
4
3 + 1 3 + 1 1 + 3
= = ⋅ tan(−195°) = tan(30° − 225°)
1 − 3 1 − 3 1 + 3
=
tan 30° −tan 225°
=
4 + 2 3
−2
= −2 − 3 1 + tan 30° tan 225°
=
tan 30° −tan 45°
16. 165° = 135° + 30°
sin 165° = sin (135° + 30°)
= sin 135° cos 30° + sin 30° cos 135°
1 + tan 30° tan 45°
3 
3
− 1
3 − 3 3 − 3
= = ⋅
= sin 45° cos 30° − sin 30° cos 45°
3 
1 +
3 + 3 3 − 3
3
2 3 1 2
= ⋅ − ⋅
2 2 2 2

=
−12 + 6 3
= −2 + 3
6
=
2
3 − 1
4 18. 225° = 300° − 45°
cos 165° = cos (135° + 30°)
= cos 135° cos 30° − sin 135° sin 30°
= −cos 45° cos 30° − sin 45° cos 30°
sin 255° = sin(300° − 45°)
= sin 300° cos 45° − sin 45° cos 300°
= −sin 60° cos 45° − sin 45° cos 60°
2 3 2 1
= − ⋅ − ⋅ = −
3
⋅
2
−
2
⋅
1
= −
2
( 3 + 1)
2 2 2 2 2 2 2 2 4
= −
2
3 + 1
4
tan 165° = tan (135° + 30°)
cos 255° = cos(300° − 45°)
= cos 300° cos 45° + sin 300° sin 45°
= cos 60° cos 45° − sin 60° sin 45°

( )tan 135° +tan 30°
=
1 2 3 2
= ⋅ − ⋅
2
= 1 − 3
1 − tan 135° tan 30°
=
−tan 45° + tan 30°
1 + tan 45° tan 30°
−1 +
3
= 3
1 +
3
2 2 2 2 4
tan 255° = tan(300° − 45°)
tan 300° −tan 45°
=
1 + tan 300° tan 45°
=
−tan 60° − tan 45°
1 − tan 60° tan 45°
3 − 3 − 1
= −2 + 3
=
1 − 3
= 2 + 3

4 3 4 3
4 3
(
3 4
(
3 4
(
3 4
)
)
)
19.
13π
=
3π
+
π
12 4 3
sin
13π
= sin
3π
+
π 
tan
13π
= tan
3π
+
π

12 
= sin
3π
cos
π
+ cos
3π
sin
π

12 
tan
3π
+ tan
π
4 3 4 3

=
2 1 2 3 
1 − tan
3π
tan
π
= ⋅ + − 
4 3
2 2
=
2
(1 −
2 2 
3)

=
−1 + 3
( )4 1 − −1 ( 3)
cos
13π
= cos
3π
+
π  1 − 3 1 − 3
12 4 3
 = − ⋅
1 + 3 1 − 3
= cos
3π
cos
π
− sin
3π
sin
π 4 − 2 3
4 3 4 3
= −
−2
2 1 2 3
= − ⋅ − ⋅
2
= − 1 + 3 = 2 − 3
20.
19π
2 2 2 2 4
π 5π
= +
12 3 4
sin
19π
= sin
π 5π 
+

12 
= sin
π
cos
5π
+ sin
5π
cos
π
3 4 4 3
3
= −
2 
+ −
2 1
⋅
2 2  2 2
= −
2
3 + 1
4
cos
19π
= cos
π 5π 
+

12 
= cos
π
cos
5π
− sin
π
sin
5π
3 4 3 4
1 2 
= − −
3 2 
−
2 2  2 2
2
=
4
−1 + 3
tan
19π
= tan
π
+
5π

12
tan
π
+ tan
5π

= 3 4
1 − tan
π
tan
5π
3 4
tan
π
+ tan
π
= 3 4
1 − tan
π
tan
π
3 4
3 + 1 1 + 3
= ⋅
1 − 3 1 + 3
=
4 + 2 3
−2
= −2 − 3

(
(
− =

(
= + − = (1 − )
21. −
5π
= −
π
−
π
12 4 6
sin −
π
−
π
= sin −
π
cos
π
− cos −
π
sin
π
4 6 4 6 4 6

2 3 2 1 2
= − − = − 3 + 1)
2 2  2 2 4
cos−
π
−
π
= cos −
π
cos
π
+ sin −
π
sin
π
4 6 4 6 4 6

2 3 2 1 2
= + − = 3 − 1)
2 2  2 2 4
tan −
π
tan−
π
− tan
π
π 4 6
4 6  1 + tan −
π
tan
π
4 6
−1 −
3
= 3 =
−3 − 3
−
1 + (−1)
3 3 3
3


=
−3 − 3
⋅
3 + 3
3 − 3 3 + 3
22. −
7π
= −
π
=
−12 − 6 3
6
−
π
= −2 − 3
12 3 4
sin−
7π
= sin−
π
−
π
= sin−
π
cos
π
− cos −
π
sin
π
12

3 4

3 4

3 4
3 2 1 2 2
= − − = −
3 + 1)

2 2  2 2 4
cos−
7π
= cos−
π
−
π
= cos−
π
cos
π
+ sin−
π
sin
π
12

3 4

3 4

3 4

1 2 3 2 2
3
2 2  2 2 4
tan−
7π
= tan−
π

π 3 4
tan−
π
− tan
π 
− =

=
− 3 − 1
= 2 + 3
12  3 4 
1 + tan−
π
tan
π  1 + (− 3)(1)
3 4

− = − (
− − = (
(
(
(

)
23. 285° = 225° + 60°
sin 285° = sin(225° + 60°) = sin 225° cos 60° + cos 225° sin 60°
2 1 2 3 2
= −  3 + 1)
2 2 2 2 4
cos 285° = cos(225° + 60°) = cos 225° cos 60° − sin 225° sin 60°
2 1 2 3 2
= −  3 − 1)
2 2  2 2 4
tan 285° = tan(225° + 60°) =
tan 225° +tan 60°
1 − tan 225° tan 60°
1 + 3 1 + 3
= ⋅ =
4 + 2 3
= −2 − 3 = −(2 + 3)
1 − 3 1 + 3 −2
24. 15° = 45° − 30°
sin 15° = sin(45° − 30°) = sin 45° cos 30° − cos 45° sin 30°
2 3 2 1 2( 3 − 1) 2
= − = = 3 − 1)
2 2  2 2 4 4
cos 15° = cos(45° − 30°) = cos 45° cos 30° + sin 45° sin 30°
2 3 2 1 2( 3 + 1) 2
= + = = 3 + 1)
2 2  2 2 4 4
tan 15° = tan(45° − 30°) =
tan 45° −tan 30°
1 + tan 45° tan 30°
1 −
3 3 − 3
= 3 = 3 =
3 − 3
⋅
3 − 3 12 − 6 3
= = 2 − 3
3  3 + 3 3 + 3 3 − 3 6
1 + (1)
3 3
25.

−165° = −(120° + 45°)
sin(−165°) = sin−(120° + 45°) = −sin(120° + 45°) = −[sin 120° cos 45° + cos 120° sin 45°]
3 2 1 2 2
( 3 1)= −

⋅ − ⋅
2 2 2 2
= − −
4
cos(−165°) = cos−(120° + 45°) = cos(120° + 45°) = cos 120° cos 45° − sin 120° sin 45°
1 2 3 2
= − ⋅ − ⋅
2
= − 1 + 3
2 2 2 2 4
tan(−165°) = tan−(120° + 45°) = −tan(120° + tan 45°) = −
tan 120° +tan 45°
1 − tan 120° tan 45°
= −
− 3 + 1
= −
1 − 3
⋅
1 − 3
= −
4 − 2 3
= 2 − 3

1 − (− 3)(1) 1 + 3 1 − 3 −2

= − − = − (1 +
(

7 5
8 8

)
)
26. −105 = 30° − 135°
sin(30° − 135°) = sin 30° cos 135° − cos 30° sin 135° = sin 30°(−cos 45°) − cos 30° sin 45°
1 2 3 2 2
3
2 2  2 2 4
cos(30° − 135°) = cos 30° cos 135° + sin 30° sin 135° = cos 30°(−cos 45°) + sin 30° sin 45°
3 2 1 2 2
= − + = 1 − 3

2 2  2 2 4
tan(30° − 135°) =
tan 30° −tan 135°
=
tan 30° −(−tan 45°)
1 + tan 30° tan 135°
3
− (−1)
= 3 = 2 +
3 
1 + (−1)
1 + tan 30°(−tan 45°)
3
3
27.

sin 3 cos 1.2 − cos 3 sin 1.2 = sin(3 − 1.2) = sin 1.8
36. cos
π
cos
3π
− sin
π
sin
3π
= cos
π
+
3π
16 16 16 16 16 16
28. cos
π
cos
π
− sin
π
sin
π
= cos
π
+
π 
π 2
7 5 7 5


= cos
12π
= cos =
4 2
29.
30.
35
sin 60° cos 15° + cos 60° sin 15° = sin(60° + 15°)
= sin 75°
cos 130° cos 40° − sin 130° sin 40° = cos(130° + 40°)
= cos 170°
37.
38.
cos 130° cos 10° + sin 130° sin 10° = cos(130° − 10°)
= cos 120°
1
= −
2
sin 100° cos 40° − cos 100° sin 40° = sin(100° − 40°)
= sin 60°
3
31.
tan (π 15) + tan(2π 5) =
= tan(π 15 + 2π 5) 2
1 − tan(π 15) tan(2π 5)
= tan(7π 15) 39.
tan(9π 8) − tan(π 8) 9π
= tan
−
π
32.
tan 1.1 − tan 4.6
= tan(1.1 − 4.6) = tan(−3.5)
1 + tan 1.1 tan 4.6
1 + tan(9π 8) tan(π 8)


= tan π
= 0
33.
34.
cos 3x cos 2y + sin 3x sin 2y = cos(3x − 2y)
sin x cos 2x + cos x sin 2x = sin(x + 2x) = sin(3x)
40.
tan 25° +tan 110°
= tan(25° + 110°)
1 − tan 25° tan 110°
= tan 135°
= −1
35. sin
π
cos
π
+ cos
π
sin
π
= sin
π
+
π
12 4 12 4 12 4 
= sin
π
3
3

(15, 8
17
v
17 17 15
− −
− +
5 85

4 15

−
25 25 24
For Exercises 41–46, you have:
sin u = – 3, u in Quadrant IV cos u = 4, tan u = – 4
5 5 3
cos v = 15, v in Quadrant I sin v = 8 , tan v = 8
y y
)
u
x x
5
(4, −3)
41.
Figures for Exercises 41–46
sin(u + v) = sin u cos v + cos u sin v
= −
3 15
+
4 8 
44. csc(u − v) =
1
=
1
( )
517 517

sin u − v
1
sin u cos v − cos u sin v

13 =
3 15 4 8 
= − 
85
517 517
1 85
42. cos(u − v) = cos u cos v + sin u sin v
=
4 15
+ −
3 8 
= = −
−
77 77
85
517

517
 1 1
 45. sec(v − u) =
cos(v − u)
=
cos v cos u + sin v sin u
60 −24 36
= + = 1 1
85 85 85 =
15 4 8  =
3 60  24
3 8  
+ −
17 5 17
1 85
+ −

85
43. tan(u + v) =
tan u + tan v
=
4 15 =
36
=
36
1 − tan u tan v
1 − −
3 8
85
415
−
13
60 13 5

13 tan u + tan v
−
3
+
8 
= = − = − 46. tan(u + v) = =
3 8
1 +
32
60
60 7 84 1 − tan u tan v 1 − −

415
13
= 60
7
5
= −
13
84
1 1 84
For Exercises 47– 52, you have:
sin u = – 7 , u in Quadrant III cos u = – 24, tan u = 7
cot(u + v) = =
tan(u + v)
= −
−
13 13
84

u
25
(−24, −7)
cos v = – 4, v in Quadrant III sin v = – 3, tan v = 3
5 5 4
y y
v
x x
5
(−4, −3)

25 5 25 5
25 5 25 5
25 5 25 5
24 4
− 5 25 5 
4 24
(
=
=
47. cos(u + v) = cos u cos v − sin u sin v
51. csc(u − v) =
1
=
1
= (− 24
)(− 4
) − (− 7
)(− 3
) sin(u − v) sin u cos v − cos u sin v
1
3 =
5 7 
− −

4 
− −

24 3
− 
48. sin(u + v) = sin u cos v + cos u sin v
= (− 7
)(− 4
) + (− 24
)(− 3
)
1
=
44
−
125
= 28
+ 72
= 100
= 4
49.
125 125 125 5
tan(u − v) =
tan u − tan v
1 + tan u tan v
7 3 11
52.
125
= −
44
sec(v − u) =
1
cos(v − u)
− −
24 4 24 44 1
= = = −
1 +
7 3 39
32
117 =
cos v cos u + sin v sin u
1
=
50. tan(v − u) =
tan v − tan u
=
3 7 

4 24
4
− −

24 
+ −

3
−

7 
25
1 + tan v tan u
11
1 +
3 7 

1
=
117
125
125
= 24 44
=
39 117
32
117
1 1 117
cot(v − u) =
tan(v − u)
=
44
=
44
117
53. sin(arcsin x + arccos x) = sin(arcsin x) cos(arccos x) + sin(arccos x) cos(arcsin x)
= x ⋅ x + 1 − x2
⋅ 1 − x2
= x2
+ 1 − x2
= 1 1
x
1
1 − x2
θ θ
1 − x2 x
54. sin(arctan 2x − arccos x) = sin(arctan 2x − arccos x)
θ = arcsin x θ = arccos x
= sin(arctan 2x) cos(arccos x) − cos(arctan 2x) sin(arccos x)
=
2x
(x) −
1
4x2
+ 1 4x2
+ 1
1 − x2
)
2x2
−
=

1 − x2
4x2
+ 1
4x2 + 1
2x 1
1 − x2
θ
1
θ = arctan 2x
θ
x
θ = arccos x

(
55. cos(arccos x + arcsin x) = cos(arccos x) cos(arcsin x) − sin(arccos x) sin(arcsin x)
= x ⋅
= 0
(Use the triangles in Exercise 53.)
1 − x2
− 1 − x2
⋅ x
56. cos(arccos x − arctan x) = cos(arccos x − arctan x)
= cos(arccos x) cos(arctan x) + sin(arccos x) sin(arctan x)
= (x)
1
+ ( 1 − x2
) x

=
x + x
1 + x2

1 − x2
1 + x2

1
1 − x2
1 + x2
x
1 + x2
θ
x
θ = arccos x
θ
1
θ = arctan x
57. sin
π
− x = sin
π
cos x − cos
π
sin x 59. sin
π
+ x = sin
π
cos x + cos
π
sin x
2 2 2 6 6 6

= (1)(cos x) − (0)(sin x)
= cos x

=
5π 
1
cos x +
2
5π
3 sin x)
5π
58. sin
π
+ x = sin
π
cos x + sin x cos
π 60. cos
4
− x = cos cos x + sin
4
sin x
4
2 2 2
θ + π
= (1)(cos x) + (sin x)(0)
= cos x
tan θ + tan π tan θ + 0
= = =
tan θ
= θ
= −
2
(cos x + sin x)
2
61.
tan( )
1 − tan θ tan π 1 − (tan θ)(0) tan
1
π  tan
π
− tan θ
4 1 − tan θ
62. tan
4
− θ =
 1 + tan
π
tan θ
4
=
1 + tan θ
63. cos(π − θ) + sin
π
+ θ = cos π cos θ + sin π sin θ + sin
π
cos θ + cos
π
sin θ
2 2 2
= (−1)(cos θ) + (0)(sin θ) + (1)(cos θ) + (sin θ)(0)
= −cos θ + cos θ
= 0
64. cos(x + y) cos(x − y) = (cos x cos y − sin x sin y)(cos x cos y + sin x sin y)
= cos2
x cos2
y − sin2
x sin2
y
= cos2
x(1 − sin2
y) − sin2
x sin2
y

=
c
o
s
2
x
−
c
o
s
2
x
s
i
n
2
y
−
s
i
n
2
x
s
i
n
2
y
=
c
o
s
2
x
−
s
i
n
2
y
(
c
o
s
2
x
+
s
i
n
2
x
)
=
c
o
s
2
x
−
s
i
n
2
y



65. cos
3π
− θ = cos
3π
cos θ + sin
3π
sin θ 68. tan(π + θ) =
tan π + tan θ
2 2 2 1 − tan π tan θ

= (0)(cos θ) + (−1)(sin θ)
= −sin θ
2
0 + tan θ
=
1 − (0) tan θ
= tan θ
1 1
−2π 2π
cot(π + θ) = =
tan(π + θ) tan θ
= cot θ
5
−2
The graphs appear to coincide, so −2π 2π
cos
3π
2
− θ = −sin θ.
66.

sin(π + θ) = sin π cos θ + cos π sin θ
= (0) cos θ + (−1) sin θ
= −sin θ
69.
−5
The graphs appear to coincide, so cot(π + θ) = cot θ
sin(x + π ) − sin x + 1 = 0
sin x cos π + cos x sin π − sin x + 1 = 0
2
−2π 2π
(sin x)(−1) + (cos x)(0) − sin x + 1 = 0
−2 sin x + 1 = 0
sin x =
1
2
−2
The graphs appear to coincide, so
sin(π + θ) = −sin(θ).
70.
x =
π
,
5π
6 6
cos(x + π ) − cos x − 1 = 0
67. sin
3π
+ θ = sin
3π
cosθ + cos
3π
sin θ cos x cos π − sin x sin π − cos x − 1 = 0
2 2 2
= (−1)(cos θ) + (0)(sin θ)
= −cosθ
(cos x)(−1) − (sin x)(0) − cos x − 1 = 0
−2 cos x − 1 = 0
cos x
1
csc
3π
= −
+ θ =
1
=
1
= −sec θ 2
2

sin(3π
+ θ) −cos θ 2π 4π
2
5
x = ,
3 3
−2π 2π
−5
The graphs appear to coincide, so
csc
3π
2
+ θ = −sec θ.

71. cosx +
π
− cosx −
π
= 1
4 4

cos x cos
π
− sin x sin
π
− cos x cos
π
+ sin x sin
π
= 1
4 4

4 4

2 
−2 sin x = 1
2 
− 2 sin x = 1
sin x = −
1
2
sin x = −
2
2
x =
5π
,
7π
4 4
72. sin x +
π
− sinx −
7π
=
3
6

6 2
sin x cos
π
+ cos x sin
π
− sin x cos
7π
− cos x sin
7π
=
3
6 6

6 6 2


(sin x)
3
+ (cos x)
1
− (sin x)−
3
+ (cos x)−
1
=
3
2

2

2

2 2
73.

tan(x + π ) + 2 sin(x + π ) = 0
tan x + tan π
+ 2(sin x cos π + cos x sin π ) = 0
1 − tan x tan π
3 sin x =
3
2
sin x =
1
2
x =
π
,
5π
6 6
tan x + 0
+ − + =
1 − tan x(0)
2 sin x( 1) cos x(0) 0
tan x
− 2 sin x = 0
1
sin x
cos x
= 2 sin x
sin x = 2 sin x cos x
sin x(1 − 2 cos x) = 0
sin x = 0 or cos x =
1
2
x = 0, π x =
π
,
5π
3 3

1  4 4
1
3 4
3
74. sin x +
π
− cos2
x = 0 76. tan(x + π ) − cosx +
π
= 0
2

2
sin x cos
π

+ cos x sin
π
− cos2
x = 0

x = 0, π
2 2
(sin x)(0) + (cos x)(1) − cos2
x = 0
cos x − cos2
x = 0
cos x(1 − cos x) = 0
cos x = 0 or 1 − cos x = 0
4
0 2π
−4
x =
π
,
3π
2 2
cos x = 1
77. sin x +
π
+ cos2
x = 0
x = 0 2

75. cosx +
π
+ cosx −
π
= 1
4 4

Graph y = cosx +

π 
+ cosx −

π 
and y2

= 1. 0 2π
x =
π
,
7π
4 4
2
−1
x =
π
, π,
3π
2 2
0 2π
78. cosx −
π
− sin2
x = 0
2


−2
1
0 2
79. y =
1
sin 2t +
1
cos 2t
3 4
−3
x = 0,
π
, π
2
(a) a =
1
, b =
1
, B = 2
3 4
C = arctan
b
a
= arctan
3
≈ 0.6435
4
y ≈
1 2 2
+

sin(2t + 0.6435) =
5
sin(2t + 0.6435)

12
(b) Amplitude:
5
12
feet
(c) Frequency:
1
=
B
=
2
=
1
cycle per second
period 2π 2π π

λ
λ
λ T λ
λ λT T 
t x
80. y1 = A cos 2π − 
T
t x 
y2 = A cos 2π + 
T 
t x t x
y1 + y2 = A cos 2π
T
− + A cos 2π + 
t x t x  t x t x t x
y1 + y2 = Acos 2π

cos 2π
λ
+ sin 2π
T
sin 2π + Acos 2π

cos 2π
λ
− sin 2π
T
sin 2π = 2A cos 2π
T
cos 2π
λ
81. True.
sin(u + v) = sin u cos v + cos u sin v
sin(u − v) = sin u cos v − cos u sin v
So, sin(u ± v) = sin u cos v ± cos u sin v.
82. False.
cos(u + v) = cos u cos v − sin u sin v
cos(u − v) = cos u cos v + sin u sin v
So, cos(u ± v) = cos u cos v sin u sin v.
83. sin(α + β) = sin α cos β + sin β cos α = 0
sin α cos β + sin β cos α
sin α cos β
= 0
= −sin β cos α
False. When α and β are supplementary, sin α cos β = −cos α sin β.
84. cos(A + B) = cos(180° − C)
= cos(180°) cos(C) + sin(180°) sin(C)
= (−1) cos(C) + (0) sin(C)
= −cos(C)
True. cos(A + B) = −cos C. When A, B and C form Δ ABC, A + B + C = 180°, so A + B = 180° − C.
85. The denominator should be 1 + tan x tan(π 4).
tan x −
π
=
tan x − tan(π 4)
87. cos(nπ + θ) = cos nπ cos θ − sin nπ sin θ
= (−1)n
(cos θ) − (0)(sin θ)
4

1 + tan x tan(π 4)
=
tan x − 1
1 + tan x 88. sin(nπ
= (−1)
n
(cos θ), where n is an integer.
+ θ) = sin nπ cos θ + sin θ cos nπ
n
86. (a) Using the graph, sin(u + v) ≈ 0 and
sin u + sin v ≈ 0.7 + 0.7 = 1.4. Because
= (0)(cos θ) + (sin θ)(−1)
= (−1)
n
(sin θ), where n is an integer.
0 ≠ 1.4, sin(u + v) ≠ sin u + sin v.
(b) Using the graph, sin(u − v) ≈ −1and
sin u − sin v ≈ 0.7 − 0.7 = 0. Because
89.
−1 ≠ 0,
C = arctan
b
sin(u − v) ≠ sin u − sin v.
sin C =
b
, cos C =
a
a a2
+ b2
a2
+ b2

a2
+ b2
sin(Bθ + C) =
a b 
a2
+ b2
sin Bθ ⋅ + ⋅ cos Bθ = a sin Bθ + b cos Bθ
a2
+ b2
a2
+ b2
90. C = arctan
a
sin C =
a
, cos C =
b
b a2
+ b2
a2
+ b2
a2
+ b2
cos(Bθ − C) =
b a 
a2
+ b2
cos Bθ ⋅ + sin Bθ ⋅

= b cos Bθ + a sin Bθ
a2
+ b2
= a sin Bθ + b cos Bθ
a2
+ b2


θ


91. sin θ + cos θ
a = 1, b = 1, B = 1
94. sin 2θ + cos 2θ
a = 1, b = 1, B = 2
(a) C = arctan
b
a
= arctan 1 =
π
4 (a) C = arctan
b
a
= arctan(1) =
π
4
sin θ + cos θ = a2
+ b2
sin(Bθ + C) sin 2θ + cos 2θ = a2
+ b2
sin(Bθ + C)
π 
= 2 sinθ + 
= 2 sin2θ +
π
(b) C = arctan
a
b
4 
= arctan 1 =
π
4 (b) C = arctan
a
4 
= arctan(1) =
π
sin θ + cos θ =
=
a2
+ b2
cos(Bθ − C)
b 4
π ( )
2 cosθ −

4 
sin 2θ + cos 2θ =
=
a2
+ b2
cos Bθ − C
2 cos2θ −
π
4

92. 3 sin 2θ + 4 cos 2θ 
a = 3, b = 4, B = 2 b π
(a) C = arctan
b
= arctan
4
≈ 0.9273
95. C = arctan
a
= a = b, a > 0, b > 0
4
a
3 sin 2θ + 4 cos 2θ =
3
a2
+ b2
sin(Bθ + C)
a2
+ b2
B = 1
= 2 a = b = 2
≈ 5 sin(2θ + 0.9273)
2 sin +
π
= 2 sin θ + 2 cos θ
(b) C = arctan
a
b
= arctan
3
4
≈ 0.6435
4
3 sin 2θ + 4 cos 2θ = a2
+ b2
cos(Bθ − C) 96. C = arctan
b
=
π
a 4
a = b, a > 0, b > 0
93. 12 sin 3θ + 5 cos 3θ
a = 12, b = 5, B = 3
≈ 5 cos(2θ − 0.6435)
a2
+ b2
B = 1
= 5 a = b =
5 2
2
(a) C = arctan
b
= arctan
5
≈ 0.3948
π 5 2 5 2
5 cosθ − = sin θ + cos θ
a
12 sin 3θ + 5 cos 3θ
12
= a2
+ b2
sin(Bθ + C) 97.
4 2 2
y
(b) C = arctan
a
b
≈ 13 sin(3θ + 0.3948)
= arctan
12
≈ 1.1760
5
≈ 13 cos(3θ − 1.1760)
y1 = m1x + b1
θ
δ
α β
x
y2 = m2x + b2

m1 = tan α and m2 = tan β
β + δ = 90° δ = 90° − β
α + θ + δ = 90° α + θ + (90° − β)
= 90° θ = β − α
So, θ = arctan m2 − arctan m1. For y = x and
y = 3x you have m1 = 1 and m2 = 3.
θ = arctan 3 − arctan 1 = 60° − 45° = 15°

  
2 2
B
98. For m2 > m1 > 0, the angle θ between the lines is: 99. y1 = cos(x + 2), y2
2
= cos x + cos 2
m2 − m1 
θ = arctan 
1 + m1m2 
m2 = 1
1
y2
0 2π
y1
m1 =
3
1 −
1 
−2
No, y1 ≠ y2 because their graphs are different.

θ = arctan 3 = arctan(2 −
1 +
1 
3) = 15°
100. y1 = sin(x + 4), y2
2
= sin x + sin 4
3

y1
0 2π
y2
−2
No, y1 ≠ y2 because their graphs are different.
101. (a) To prove the identity for sin(u + v) you first need to prove the identity for cos(u − v).
y
C 1 u − v
Assume 0 < v < u < 2π and locate u, v, and u − v on the unit circle. B
The coordinates of the points on the circle are: D
A = (1, 0), B = (cos v, sin v), C = (cos(u − v), sin(u − v)), and D = (cos u, sin u).
Because ∠DOB = ∠COA, chords AC and BD are equal. By the Distance Formula:
−1
u
v A x
O 1
2 2 2 2
cos(u − v) − 1 + sin(u − v) − 0 = (cos u − cos v) + (sin u − sin v) −1
cos2
(u − v) − 2 cos(u − v) + 1 + sin2
(u − v) = cos2
u − 2 cos u cos v + cos2
v + sin2
u − 2 sin u sin v + sin2
v
cos2
(u − v) + sin2
(u − v) + 1 − 2 cos(u − v) = (cos2
u + sin2
u) + (cos2
v + sin2
v) − 2 cos u cos v − 2 sin u sin v
2 − 2 cos(u − v) = 2 − 2 cos u cos v − 2 sin u sin v
−2 cos(u − v) = −2(cos u cos v + sin u sin v)
cos(u − v) = cos u cos v + sin u sin v
Now, to prove the identity for sin(u + v), use cofunction identities.
sin(u + v) = cos
π
− (u + v) = cos
π
− u − v
2

2
= cos
π
2
− u cos v + sin
π
2
− u sin v

= sin u cos v + cos u sin v
(b) First, prove cos(u − v) = cos u cos v + sin u sin v using the figure containing points
A(1, 0)
B(cos(u − v), sin(u − v))
C(cos v, sin v)
y
1 D
u − v
C
u
v
A x
D(cos u, sin u)
on the unit circle.
−1 u − v 1
Because chords AB and CD are each subtended by angle u − v, their lengths are equal. Equating −1

2 2

 
2
d(A, B) = d(C, D) you have (cos(u − v) − 1) + sin2
(u − v) = (cos u − cos v) + (sin u − sin v) .
Simplifying and solving for cos(u − v), you have cos(u − v) = cos u cos v + sin u sin v.
Using sin θ = cos
π
2

− θ ,


sin(u − v) = cos
π
2
− (u − v) = cos
π
2
− u − (−v) = cos
π
2
− u cos(−v) + sin
π
2
− u sin(−v)

= sin u cos v − cos u sin v


h 0.5 0.2 0.1 0.05 0.02 0.01
f (h) 0.267 0.410 0.456 0.478 0.491 0.496
g(h) 0.267 0.410 0.456 0.478 0.491 0.496
= −
= −
102. (a) The domains of f and g are the same, all real numbers h, except h = 0.
(b) (c) 2
(d) As h → 0*,
f → 0.5 and
−3 3
−2
Section 2.5 Multiple-Angle and Product-to-Sum Formulas
g → 0.5.
1. 2 sin u cos u
2. cos2
u − sin2
u = 2 cos2
u − 1 = 1 − 2 sin2
u
8. sin 2x sin x = cos x
2 sin x cos x sin x − cos x = 0
cos x(2 sin2
x − 1) = 0
1
3.
2
sin(u + v) + sin(u − v)
cos x = 0 or 2 sin2
x =
π
+ 2nπ
x − 1 = 0
sin2
x =
1
4. tan2
u
2 2
sin x = ±
2
2
5. ±
1 − cos u
2 x =
π
+
nπ
6. −2 sin
u + v
sin
u − v
4 2
9. cos 2x − cos x = 0
2 2 
7. sin 2x − sin x = 0
2 sin x cos x − sin x = 0
sin x(2 cos x − 1) = 0
sin x = 0 or 2 cos x − 1 = 0
cos 2x = cos x
cos2
x − sin2
x = cos x
cos2
x − (1 − cos2
x) − cos x = 0
2 cos2
x − cos x − 1 = 0
(2 cos x + 1)(cos x − 1) = 0
x = nπ cos x =
1
2
2 cos x + 1 = 0 or cos x − 1 = 0
x =
π
+ 2nπ,
5π
+ 2nπ cos x
1
cos x = 1
10.
3 3
cos 2x + sin x = 0
1 − 2 sin2
x + sin x = 0
2 sin2
x − sin x − 1 = 0
(2 sin x + 1)(sin x − 1) = 0
2
x =
2nπ
3
x = 0
2 sin x + 1 = 0 or sin x − 1 = 0
sin x
1
2
sin x = 1
x =
7π
+ 2nπ,
11π
+ 2nπ x =
π
+ 2nπ
6 6 2

( )
Section 2.5 Multiple Angle and Product-to-Sum Formulas 259
11. sin 4x = −2 sin 2x
sin 4x + 2 sin 2x = 0
2 sin 2x cos 2x + 2 sin 2x = 0
2 sin 2x(cos 2x + 1) = 0
2 sin 2x = 0 or cos 2x + 1 = 0
sin 2x = 0 cos 2x = −1
2x = nπ 2x = π + 2nπ
x =
n
π x =
π
+ nπ
2 2
12. (sin 2x + cos 2x)
2
= 1
sin2
2x + 2 sin 2x cos 2x + cos2
2x = 1
2 sin 2x cos 2x = 0
sin 4x = 0
4x = nπ
x =
nπ
4
13. tan 2x − cot x = 0
2tan x
= cot x
1 − tan2
x
2 tan x = cot x(1 − tan2
x)
2 tan x = cot x − cot x tan2
x
2 tan x = cot x − tan x
3 tan x = cot x
3 tan x − cot x = 0
3 tan x −
1
= 0
tan x
3 tan2
x − 1
= 0
tan x
1
3 tan2
x − 1 = 0
tan x
cot x(3 tan2
x − 1) = 0
cot x = 0 or 3 tan2
x − 1 = 0
x =
π
+ nπ tan2
x =
1
2 3
tan x = ±
x =
π
3
3
+ nπ,
5π
+ nπ
6 6

tan 2x − 2 cos x 0
2tan x
1 − tan2
x
2 cos x
2 tan x
2 tan x
2 cos x(1 − tan2
x)
2 cos x − 2 cos x tan2
x
cos x 
2
2
=
14. =
=
=
=
2 tan x = 2 cos x − 2 cos x
sin2
x
cos2
x
2 tan x = 2 cos x − 2
sin2
x
cos x
sin x sin2
x
tan x = cos x −
sin x
= cos x −
cos x
sin2
x
cos x
sin2
x
cos x
cos x
+ − cos x = 0
cos x
sin x + sin2
x − cos2
x
= 0
cos x
1
sin x + sin2
x − (1 − sin2
x) = 0
sec x2 sin2
x + sin x − 1 = 0
sec x(2 sin x − 1)(sin x + 1) = 0
sec x = 0 or 2 sin x − 1 = 0 or sin x + 1 = 0
No solution
sin x =
1 sin x = −1
2 3π
x =
x =
π
,
5π 2
6 6
Also, values for which cos x = 0 need to be checked.
π
,
3π
are solutions.
2 2
x =
π
+ 2nπ,
π
+ nπ,
5π
+ 2nπ
15.
6 2 6
6 sin x cos x = 3(2 sin x cos x)
= 3 sin 2x
19. 4 − 8 sin2
x = 4(1 − 2 sin2
x)
= 4 cos 2x
16. sin x cos x =
=
1
(2 sin x cos x)
1 sin 2x
20. 10 sin2
x − 5 = 5(2 sin2
x − 1)
2
17.
2
6 cos2
x − 3 = 3(2 cos2
x − 1)
= 3 cos 2x
= −5(1 − 2 sin x)
= −5 cos 2x
18. cos2
x − 1
= 1 2(cos2
x − 1
)
2 2 2 
= 1
(2 cos2
x − 1)
1 cos 2x

5
3
u
−4
u
4
5
−
34
3
5
, ,
2  2 
3
tan 2u = = 

2 
2
= −
21. sin u
3 3π
= −
5 2
y
< u < 2π 22. cos u
4 π
5 2
y
< u < π
x x
3
sin 2u = 2 sin u cos u = −
3 4
= −
24
sin 2u = 2 sin u cos u =
3
−
4 24
= −
5 5 25 5 5 25
cos 2u = cos2
u − sin2
u =
16
−
9
=
7
25 25 25
3
2− 
cos 2u = cos2
u − sin2
u =
16
−
9
=
7
25 25 25

2−
tan 2u =
2tan u
=
4 316 24 2tan u 4 316 24
= − = − tan 2u = =
9
= − = −
23.
1 − tan2
u
tan u =
3
, 0 < u <
π
5 2
1 −
9
16
2 7 7 1 − tan2
u
1 −
16
2 7 7
y 3 5 15 sin
2u = 2 sin u cos u = 2 =
34 34 17
cos 2u = cos2
u − sin2
u =
25
−
9
=
8
34 34 17
3
2u x 2tan u 5
=
6 25
=
15
24. sec u = −2, π < u <
3π
2
1 − tan2
u 1 −
9
25
5 16 8
y
sin 2u = 2 sin u cos u = −
3
−
1
=
3
2 2 2
cos 2u = cos2
u − sin2
u = −
1
2
3 
− − =
1
−
3
= −
1
u
2 2  4 4 2
−1 x 3 
2
2 tan u 1 2 3
− 3 2 tan 2u =
1 − tan2
u
= 2
= = − 3
3 −2
1 −
1
25. cos 4x = cos(2x + 2x)
= cos 2x cos 2x − sin 2x sin 2x
= cos2
2x − sin2
2x
= cos2
2x − (1 − cos2
2x)
= 2 cos2
2x − 1
=
2
(
c
o
s
2
x)
2
− 1

1 − tan2
x
=
2
=

2
6.
tan 3x = tan(2x + x)
=
tan
2x +
tan x
1 − tan 2x tan x
2
t
a
n
x
1 − tan2
x
+ tan x
1 −
2 tan x
(tan x)

2 tan x + tan x − tan3
x
= 2(2 cos2
x − 1) − 1 1 − tan2
x
2 2
= 2(4 cos4
x − 4 cos x + 1) − 1 1 − tan x − 2 tan x
1 − tan2
x
= 8 cos4
x − 8 cos x + 1
3 tan x tan3
x
=
−
1 − 3 tan2
x

2
=
1 cos 2x 1 cos 2x
3

2
27. cos4
x = (cos2
x)(cos2
x) =
1 + cos 2x1 + cos 2x
=
1 + 2 cos 2x + cos 2x
2 2 4
1 + 2 cos 2x +
1 + cos 4x
= 2
4
=
2 + 4 cos 2x + 1 + cos 4x
8
=
3 + 4 cos 2x + cos 4x
8
=
1
(3 + 4 cos 2x + cos 4x)
8
8 4 4 2
2
2
2
28. sin x = (sin x)(sin x) = (sin x) (sin x)
2 2
− − 
2 2 
1 − 2 cos 2x + cos2
2x1 − 2 cos 2x + cos2
2x
= 
4 4 
1 − 2 cos 2x + cos2
2x − 2 cos 2x + 4 cos2
2x − 2 cos3
2x + cos2
2x − 2 cos3
2x + cos4
2x
=
16
1 − 4 cos 2x + 6 cos2
2x − 4 cos3
2x + cos4
2x
=
16
2 3 2
2
1 − 4 cos 2x + 6 cos 2x − 4 cos 2x + (cos 2x)=
16
1 + cos 4x 1 + cos 4x
1 − 4 cos 2x + 6 − 4 cos 2x + 
=
2 2 
16
1 + 2 cos 4x + cos2
4x
1 − 4 cos 2x + 3 + 3 cos 4x − 4 cos3
2x + 
=
4

16
4 − 16 cos 2x + 12 + 12 cos 4x − 16 cos3
2x + 1 + 2 cos 4x + cos2
4x
=
64
17 − 16 cos 2x + 14 cos 4x − 16 cos3
2x +
1 + cos 8x
=
2 
64
34 − 32 cos 2x + 28 cos 4x − 32 cos3
2x + 1 + cos 8x
=
128
35 − 32 cos 2x + 28 cos 4x − 32 cos3
2x + cos 8x
=
128
35 − 32 cos 2x + 28 cos 4x − 32 cos2
2x cos 2x + cos 8x
=
128
1 + cos 4x
35 − 32 cos 2x + 28 cos 4x − 32
2
cos 2x + cos 8x
=
128
=
35 − 32 cos 2x + 28 cos 4x − 16 cos 2x − 16 cos 4x cos 2x + cos 8x
128
=
35 − 48 cos 2x + 28 cos 4x − 16 cos 4x cos 2x + cos 8x
128
=
1
(35 − 48 cos 2x + 28 cos 4x + cos 8x − 16 cos 2x cos 4x)
128

=
1 cos 4x
( 2
)

=
1 cos 4x

( 2
)
( 2
)
2 2

2


29. sin4
2x = (sin2
2x) 31. tan4
2x = (tan2
2x)
2
−  
2
1 − cos 4x
=
2  1 + cos 4x
1
= 1 − 2 cos 4x + cos 4x
4
=
1
1 − 2 cos 4x +
1 + cos 8x
1 − 2 cos 4x + cos2
4x
=
1 + 2 cos 4x + cos2
4x
1 + cos 8x
4 2 
1 1 1 1
= − cos 4x + + cos 8x
4 2 8 8
3 1 1
= − cos 4x + cos 8x
8 2 8
1
= (3 − 4 cos 4x + cos 8x)
8
1 − 2 cos 4x +
= 2
1 + 2 cos 4x +
1 + cos 8x
2
1
(2 − 4 cos 4x + 1 + cos 8x)
= 2
1
(2 + 4 cos 4x + 1 + cos 8x)
2
=
3 − 4 cos 4x + cos 8x
30. cos4
2x = (cos2
2x) 3 + 4 cos 4x + cos 8x
2
+   32. tan2
2x cos4
2x =
1 − cos 4x
(cos2
2x)
2
2 
=
1
(1 + 2 cos 4x + cos2
4x)
1 + cos 4x
1 − cos 4x 1 + cos 4x
2
4 =
1 + cos 4x 2
1 1 + cos 8x 
= 1 + 2 cos 4x +

(1 − cos 4x)(1 + cos 4x)(1 + cos 4x)
4 2 
1 1 1 1
= + cos 4x + + cos 8x
4 2 8 8
3 1 1
= + cos 4x + cos 8x
8 2 8
1
= (3 + 4 cos 4x + cos 8x)8
=
4(1 + cos 4x)
(1 − cos 4x)(1 + cos 4x)=
4
1
= 1 − cos 4x
4
=
1
−
1 + cos 8x
1
4 2
33. sin2
2x cos2
2x =
1 − cos 4x1 + cos 4x
1 1 1
= − − cos 8x
4 8 8
1 1
= − cos 8x
8 8
1
= (1 − cos 8x)
8
2 2


1
= 1 − cos 4x
4
1 1 + cos 8x
= 1 −
4 2


=
1
−
1
−
1
cos 8x
4 8 8
=
1
−
1
cos 8x

( 2
)
( 2 3
)
[ ]
[ ]
2 +
3
34. sin4
x cos2
x = sin2
x sin2
x cos2
x
=
1 − cos 2x1 − cos 2x1 + cos 2x
2

2 2

1
= (1 − cos 2x) 1 − cos 2x
8
1
= 1 − cos 2x − cos 2x + cos 2x
8
+ +1 1 cos 4x 1 cos 4x
= 1 − cos 2x − + cos 2x
8  2  2
1
= 2 − 2 cos 2x − 1 − cos 4x + cos 2x + cos 2x cos 4x
16
1
= 1 − cos 2x − cos 4x + cos 2x cos 4x
16
1 1 − cos 150° 1 + ( 3 2)
35. sin 75° = sin ⋅ 150° = =
2 2 2
=
1
2 + 3
2
1 1 + cos 150° 1 − ( 3 2)
cos 75° = cos ⋅ 150° = =
2 2 2
=
1
2 − 3
2
tan 75° = tan
1
⋅ 150° =
sin 150°
=
1 2
2

1 + cos 150° 1 ( 3 2)−
1 2 + 3
= ⋅ =
2 + 3
= 2 + 3
2 − 3 2 +
1 
3 4 − 3
1 − cos 330° 1 − ( 3 2)
36. sin 165° = sin ⋅ 330° = =
2 2 2
=
1
2 − 3
2
1 1 + cos 330° 1 + ( 3 2)
cos 165° = cos ⋅ 330° = − = −
2 2 2
1
= −
2
tan 165° = tan
1
⋅ 330° =
sin 330°
=
−1 2
2

1 + cos 330° 1 ( 3 2)+
−1 2 − 3 −2 + 3
= ⋅ = = −2 + 3
2 + 3 2 − 3 4 − 3

1
1 1 − cos 225° 1 − (− 2 2) 1
37. sin 112° 30′ = sin ⋅ 225° = = = 2 + 2
2  2 2 2
1 1 + cos 225° 1 + (− 2 2) 1
cos 112° 30′ = cos ⋅ 225° = − = − = − 2 − 2
2  2 2 2
tan 112° 30′ = tan
1
⋅ 225° =
sin 225°
=
− 2 2
=
− 2
⋅
2 + 2
=
−2 2 − 2
= −1 − 2
2

1 + cos 225° 1 ( 2 2) 2 − 2 2 + 2 2
+ −
1 1 − cos 135° 1 + ( 2 2) 1
38. sin 67° 30′ = sin ⋅ 135° = = = 2 + 2
2  2 2 2
1 1 + cos 135° 1 − ( 2 2) 1
cos 67° 30′ = cos ⋅ 135° = = = 2 − 2
2  2 2 2
tan 67° 30′ = tan
1
⋅ 135° =
sin 135°
=
2 2
= 1 + 2
2

1 + cos 135° 1 ( 2 2)−
π 1π  1 − cos
π
4 1
39. sin = sin = = 2 − 2
8 2 4 2 2
π
π 1π  1 + cos
4
cos = cos = = 2 + 2
8 2 4 2 2
sin
π 2
tan
π
= tan
1π
= 4 = 2 = 2 − 1
8 2 4  1 + cos
π
1 +
2
4 2
40. sin
7π
= sin
1 7π
=
1 − cos
7π
6 =
1 +
3
2 =
1
2 + 3
12 2 6

2 2 2
1 + cos
7π
1 −
3
cos
7π
= cos
1 7π
= − 6 = − 2 = −
1
2 − 3
12 2 6

2 2 2
sin
7π
−
1
tan
7π
= tan
1 7π
= 6 = 2 = −2 − 3
12 2 6  1 + cos
7π
1 −
3
6 2

2
2
,
2
2
= −




41. cos u =
7
, 0 < u <
π
42. sin u =
5
,
π
< u < π cos u
12
25 2
(a) Because u is in Quadrant I,
u
is also in Quadrant I.
2
1 −
7
13 2 13
(a) Because u is in Quadrant II,
u
is in Quadrant I.
2
1 +
12
(b) sin
u
=
1 − cos u
= 25 =
9 3
= (b) sin
u
=
1 − cos u
= 13 5 26
=
2 2 2 25 5
1 +
7
2 2 26
1 −
12
cos
u
=
1 + cos u
= 25 =
16 4
= cos
u
=
1 + cos u
= 13 26
=
2 2 2 25 5
1 −
7
2 2 26
5
tan
u
=
1 − cos u
= 25 =
3
tan
u
=
sin u
= 13 = 5
2 sin u 24 4 2

1 + cos u 1
12
43. tan u
5 3π
= −
12 2
25
< u < 2π
−
13
(a) Because u is in Quadrant IV,
u
is in Quadrant II.
2
1 −
12
(b) sin
u
=
1 − cos u
= 13 =
1 26
=
2 2 2 26 26
1 +
12
cos
u 1 + cos u
= − = − 13 25 5 26
= − = −
2 2 2 26 26
1 −
12
tan
u
=
1 − cos u
= 13 = −
1
2 sin u
−
5 5
13
44. cot u = 3, π

< u <
3π
2
(a) Because u is in Quadrant III,
u
is in Quadrant II.
2
1 +
3
(b) sin
u
=
1 − cos u
=
10 =
10 + 3 10
=
1 10 + 3 10
2 2 20 2 5
1 −
3
cos
u
= −
1 + cos u
= − 10 10 − 3 10
= −
1 10 − 3 10
= −
2 2 20 2 5
1 +
3
tan
u
=
1 − cos u
= 10 = − 10 − 3

45. sin
x
+ cos x = 0
2
47. cos
x
− sin x = 0
2
±
1 − cos x
2
1 − cos x
2
= −cos x
= cos2
x
±
1 + cos x
2
1 + cos x
2
= sin x
= sin2
x
cos x =
1
2
0 = 2 cos2
x + cos x − 1
= (2 cos x − 1)(cos x + 1)
or cos x = −1
1 + cos x = 2 sin2
x
1 + cos x = 2 − 2 cos2
x
2 cos2
x + cos x − 1 = 0
(2 cos x − 1)(cos x + 1) = 0
x =
π
,
5π
3 3
x = π
2 cos x − 1 = 0 or cos x + 1 = 0
2
1cos x =
2 cos x = −1
0 2π
x =
π
,
5π
3 3
x = π
−2
By checking these values in the original equation,
x = π 3 and x = 5π 3 are extraneous, and x = π
is the only solution.
x =
π
, π,
5π
3 3
π 3, π, and 5π 3 are all solutions to the equation.
2
46. h(x) = sin
x
+ cos x − 1
2
sin
x
+ cos x − 1 = 0
2
0 2π
−2
±
1 − cos x
2
1 − cos x
= 1 − cos x
= 1 − 2 cos x + cos2
x
48. g(x) = tan
x
− sin x
2
x
2
1 − cos x = 2 − 4 cos x + 2 cos2
x
tan − sin x = 0
2
1 − cos x
2 cos2
x − 3 cos x + 1 = 0 sin x
= sin x
(2 cos x − 1)(cos x − 1) = 0
2 cos x − 1 = 0 or cos x − 1 = 0
1 − cos x = sin2
x
1 − cos x = 1 − cos2
x
2
cos x =
1
cos x = 1
cos x − cos x = 0
2
x =
π
,
5π
3 3
x = 0
cos x(cos x − 1) = 0
cos x = 0 or cos x − 1 = 0
0,
π
, and
5π
are all solutions to the equation.
x =
π
,
3π
2 2
cos x = 1
3 3
x = 0
1
0,
π
, and
3π
are all solutions to the equation.
0 2π 2 2

2

π π
π
49. sin 5θ sin 3θ = 1
cos(5θ − 3θ) − cos(5θ + 3θ) = 1
(cos 2θ − cos 8θ)
2 2
50. 7 cos(−5β) sin 3β = 7 ⋅ 1
sin(−5β + 3β) − sin(−5β − 3β) = 7
(sin(−2β) − sin(−8β))
2 2
51. cos 2θ cos 4θ = 1
cos(2θ − 4θ) + cos(2θ + 4θ) = 1
cos(−2θ) + cos 6θ
2 2
52. sin(x + y) cos(x − y) = 1
(sin 2x + sin 2y) 54. sin 3θ + sin θ = 2 sin
3θ + θ
cos
3θ − θ
2 2
53. sin 5θ − sin 3θ = 2 cos
5θ + 3θ
sin
5θ − 3θ  = 2 sin 2θ cos θ
2 2 
= 2 cos 4θ sin θ 55. cos 6x + cos 2x = 2 cos
6x + 2x
cos
6x − 2x
2 2
56. cos x + cos 4x = 2 cos
x + 4x
cos
x − 4x 

= 2 cos 4x cos 2x
2 2


= 2 cos
5x
cos
−3x 
2 2


° + °

° − °

57.
75 15 75 15 2 3 6
sin 75° + sin 15° = 2 sin cos = 2 sin 45° cos 30° = 2 =
2 2

2 2 2

° + °

° − °
58.
120 60 120 60 3
cos 120° + cos 60° = 2 cos cos = 2 cos 90° cos 30° = 2(0) = 0
2 2

2
3π
+
π 3π

−
π
59. cos
3π
− cos
π
= −2 sin 4 4 sin 4 4 = −2 sin sin
4 4  2 2 2 4
cos
3π
− cos
π 2 2
= − − = − 2
4 4 2 2
5π
+
3π 5π
−
3π
60. sin
5π
− sin
3π
= 2 cos 4 4 sin 4 4 = 2 cos π sin
4 4  2 2 4
sin
5π
− sin
3π 2 2
= − − = − 2
4 4 2 2
61. sin 6x + sin 2x = 0
2 sin
6x + 2x
cos
6x − 2x
= 0
2 2


2(sin 4x) cos 2x = 0
sin 4x = 0 or cos 2x = 0

−2
2
4x = nπ 2x =
π
2
+ nπ
0 2π
x =
nπ
x =
π
+
nπ
4 4 2
In the interval [0, 2π )
x = 0,
π
,
π
,
3π
, π,
5π
,
3π
,
7π
.
4 2 4 4 2 4


62. h(x) = cos 2x − cos 6x
cos 2x − cos 6x = 0
−2 sin 4x sin(−2x) = 0
2 sin 4x sin 2x = 0
sin 4x = 0 or sin 2x = 0 2
4x = nπ 2x = nπ
0 2π
x =
nπ
x =
nπ
4 2
−2
x = 0,
π
,
π
,
3π
, π,
5π
,
3π
,
7π
x = 0,
π
, π,
3π
4 2 4 4 2 4 2 2
63.
cos 2x
− 1 = 0
sin 3x − sin x
cos 2x
= 1
sin 3x − sin x
2
cos 2x
= 1
65. csc 2θ
1
=
sin 2θ
1
=
2 sin θ cos θ
=
1
⋅
1
2 cos 2x sin x
0 2π
2 sin x = 1
sin θ
csc θ
=
2 cos θ
sin x =
1
−2
2
2 cos θ
x =
π
,
5π 66. ( )( )
cos4
x − sin4
x =
6 6 = (
cos2
x − sin2
x
cos 2x)(1)
cos2
x + sin2
x
64. f (x) = sin2
3x − sin2
x
sin2
3x − sin2
x = 0
(sin 3x + sin x)(sin 3x − sin x) = 0
(2 sin 2x cos x)(2 cos 2x sin x) = 0
67. (sin x + cos x)
2
= cos 2x
= sin2
x + 2 sin x cos x + cos2
x
= (sin2
x + cos2
x) + 2 sin x cos x
= 1 + sin 2x
sin 2x = 0 x = 0,
π
, π,
3π
or
2 2
68. tan
u 1 − cos u
=
cos x = 0 x =
π
,
3π
or
2 2
2 sin u
1 cos u
= −
cos 2x = 0 x =
π
,
3π
,
5π
,
7π
or sin u sin u
4 4 4 4
sin x = 0 x = 0, π
1
= csc u − cot u
2 sin
x ± y
cos
x y
0 2π
69.
sin x ± sin y
cos x + cos y
=
2 2 
2 cos
x + y
cos
x − y
2 2


−1
= tan
x ± y 
2
π
+ x +
π
− x
 π
+ x −
π

− x

3 

 
70.
π
cos π
+ x + cos − x = 2 cos 3 3 cos
3 3
3 3  2 2


= 2 cos
π
cos(x)

1
= 2 cos x = cos x
2

2 
=
1
2
71. (a) sin
θ
= ±

1 − cos θ
2
1
=
M (c) When M = 4.5, cos θ
(4.5)
2
− 2
=
(4.5)
2
2
1 − cos θ 
±  cos θ ≈ 0.901235.
2  M  So, θ ≈ 0.4482 radian.
1 − cos θ
2
1
=
M 2 (d) When M = 2,
speed of object
= M
speed of sound
M 2
(1 − cos θ) = 2 speed of object
= 2
1 − cos θ
−cos θ
2
=
M 2
2
= − 1
760 mph
speed of object = 1520 mph.
speed of object
cos θ
M 2
= 1 −
2
M 2
M 2
− 2
When M = 4.5,
speed of sound
speed of object
760 mph
= M
= 4.5
cos θ =
M 2
22
− 2 1 π
speed of object = 3420 mph.
(b) When M = 2, cos θ = =
22
2
. So, θ = .
3
72.
1
(75)
2
sin 2θ
32
sin 2θ
= 130
130(32)=
752
75. True. Using the double angle formula and that sine is an
odd function and cosine is an even function,
sin(−2x) = sin2(− x)
= 2 sin(− x) cos(− x)
θ =
1
sin−1
130(32)
= 2(−sin x) cos x
2 752

θ ≈ 23.85°
= −2 sin x cos x.
76. False. If 90° < u < 180°,
73.
x
= 2r sin2 θ
= 2r
1 − cos θ
2 2 2

u
is in the first quadrant and
= r(1 − cos θ) 2
So, x = 2r(1 − cos θ). sin
u
=
1 − cos u
.
74. (a) Using the graph, sin 2u ≈ 1and
2 2
77. Because φ and θ are complementary angles,
2 sin u cos u ≈ 2(0.7)(0.7) ≈ 1.
Because 1 = 1, sin 2u = 2 sin u cos u.
sin φ = cos θ and cos φ = sin θ.
(b) Using the graph, cos 2u ≈ 0 and
cos2
u − sin2
u ≈ (0.7)
2
− (0.7)
2
= 0.
(a) sin(φ − θ) = sin φ cos θ − sin θ cos φ
= (cos θ)(cos θ) − (sin θ)(sin θ)
= cos2
θ − sin2
θ
Because 0 = 0, cos 2u = cos2
u − sin2
u.
R
e
v
iew Exercises for Chapter 2

(b)
=
c
o
s
2
θ
c
o
s
(
φ
−
θ
)
=
c
o
s
φ
c
o
s
θ
+
s
i
n
φ
s
i
n
θ
=
(
s
i
n
θ
)
(
c
o
s
θ
)
+
(
c
o
s
θ
)
(
s
i
n
θ)
= 2 sin θ cos θ
= sin 2θ
1. cot x 3. cos x

2. sec x 4. cot2
x + 1 = csc2
x = csc x

= −
= −
tan2
x
2
Review Exercises for Chapter 2 271
5. cos θ
2
, tan θ
5
> 0, θ is in Quadrant III.
sec θ =
1
= −
5
cos θ 2
sin θ = − 1 − cos2
θ = − 1 −
4
= −
21
= −
21
cscθ
25 25 5
=
1
= −
5
= −
5 21
sin θ 21 21
−
21
tan θ =
sin
= 5 =
21
cos θ −
2 2
5
cot θ =
1
=
2
=
2 21
tan θ 21 21
6. cot x
2
, cos x < 0, x is in Quadrant II.
3
tan x =
1
= −
3
cot x 2
csc x = 1 + cot2
x = 1 +
4
=
13 13
=
9 9 3
sin x =
1
=
3
=
3 13
csc x 13 13
cos x = − 1 − sin2
x = − 1 −
9 4 2 2 13
= − = − = −
sec x =
1
= −
13
13 13 13 13
cos x 2
1 1
7. = = sin2
x
cot2
x + 1 csc2
x
13. cos2
x + cos2
x cot2
x = cos2
x(1 + cot2
x)
= cos2
x(csc2
x)
sin θ 1
8.
tan θ
=
cos θ
=
1 = cos2
x 
sin2
x
1 − cos2
θ sin2
θ sin θ cos θ
cos2
x
= csc θ sec θ =
sin2
x
2
9. tan2
x(csc2
x − 1) = tan2
x(cot2
x) = cot x
= tan2
x
1


14. (tan x + 1)2
cos x = (tan2
x + 2 tan x + 1) cos x
= 1
= (sec x + 2 tan x) cos x
10.

( ) cos x
=
2
cot2
x sin
2
x
=
sin2
x
=
cos2
x
s
i
n2
x
sin x 
= sec2
x cos x + 2 cos x
cos x
= sec x + 2 sin x
cot
π
− u
11.
2 
cos u
tan u
cos u
= tan u sec u
12.
sec (−θ) sec θ 1 cos θ sin θ 2
2 2 2 2
= = = = tan θcsc2
θ csc2
θ 1 sin2
θ cos2
θ

2



15.
1 1 (csc θ − 1) − (csc θ + 1)
− =
16.
tan x sec x − 1
2 2
=csc θ + 1 csc θ − 1 (csc θ + 1)(csc θ − 1)
=
−2
csc2
θ − 1
=
−2
cot2
θ
= −2 tan2
θ
1 + sec x 1 + sec x
(sec x + 1)(sec x − 1)=
sec x + 1
= sec x − 1
17. Let x = 5 sin θ, then
25 − x2
= 25 − (5 sin θ)
2
= 25 − 25 sin2
θ = 25(1 − sin2
θ) = 25 cos2
θ = 5 cos θ.
18. Let x = 4 sec θ, then
x2
− 16 = (4 sec θ)
2
− 16 = 16 sec2
θ − 16 = 16(sec2
θ − 1) = 16 tan2
θ = 4 tan θ.
19. cos x(tan2
x + 1) = cos x sec2
x 25. sin5
x cos2
x = sin4
x cos2
x sin x
1
= sec2
x
sec x
= (1 − cos2
x) cos2
x sin x
= sec x
= (1 − 2 cos x + cos x) cos x sin x
20. sec2
x cot x − cot x = cot x(sec2
x − 1)
= cot x tan2
x 26.
2 4 2
= (cos2
x − 2 cos4
x + cos6
x) sin x
cos3
x sin2
x = cos x cos2
x sin2
x
1 
= tan2
x = tan x
tan x
= cos x(1 − sin2
x) sin2
x
4
= cos x(sin2
x − sin x)
21. sin
π
2
− θ tan θ = cos θ tan θ
= (sin2
x − sin4
x) cos x

sin θ 
= cos θ 
cos θ 
= sin θ
27. sin x =
sin x =
3 − sin x
3
2
x =
π
+ 2πn,
2π
+ 2πn
22. cot
π
2
− θ csc θ
3 3
= tan θ csc θ

sin θ 1 
=
cos θ sin θ 
28. 4 cos θ
2 cos θ
= 1 + 2 cos θ
= 1
1
1
=
cos θ
cos θ =
2
π 5π

= sec θ
θ = + 2nπ or
3
+ 2nπ
3
23.
1
=
1
= cos θ 29. 3 3 tan u = 3
tan θ csc θ sin θ
cos θ
⋅
1
sin θ tan u =
1
3
π
24.
1 1 1
= =

u = + nπ
6
tan x csc x sin x (tan x)
1
(sin x)sin x tan x
= cot x

30.
1
sec x − 1 = 0
2
1
sec x = 1
2
35. cos2
x + sin x = 1
1 − sin2
x + sin x − 1 = 0
−sin x(sin x − 1) = 0
sec x = 2 sin x = 0 sin x − 1 = 0
cos x =
1
2
x = 0, π sin x = 1
x =
π
x =
π
+ 2nπ or
5π 2
+ 2nπ
31.
3 3
3 csc2
x = 4
36. sin2
x + 2 cos x = 2
1 − cos2
x + 2 cos x = 2
2
csc2
x =
4 0 = cos x − 2 cos x + 1
3
sin x = ±
3
2
0 = (cos x − 1)
2
cos x − 1 = 0
cos x = 1
x =
π
+ 2πn,
2π
+ 2πn,
4π
+ 2πn,
5π
+ 2πn x = 0
3 3 3 3
These can be combined as: 37. 2 sin 2x − 2 = 0
x =
π
+ nπ or x =
2π
+ nπ sin 2x =
2
3 3
2x =
π
+ 2πn,
3π
2
+ 2πn
32. 4 tan2
u − 1 = tan2
u 4 4
3 tan2
u − 1 = 0
x =
π
+ πn,
3π
+ πn
tan2
u =
1
3
tan u = ±
1
3
= ±
3
3
8 8
x =
π
,
3π
,
9π
,
11π
8 8 8 8
x
u =
π
+ nπ or
5π
+ nπ
38. 2 cos + 1 = 0
2
6 6 x 1
cos = −
33. sin3
x = sin x
2 2
sin3
x − sin x = 0
sin x(sin2
x − 1) = 0
sin x = 0 x = 0, π
sin2
x = 1
x
=
2π
2 3
x =
4π
3
x
sin x = ±1 x =
π
,
3π
2 2
39. 3 tan2
− 1 = 0
3
tan2 x
=
1
34.

3
= −
2
c
o
s
2
x
+
3
c
o
s
x
=
0
c
o
s
x
(
2
c
o
s
x
+
3
)
=
0
cos
x =
0
or
2
cos
x +
3 =
0

3
tan
x
=
±
1
3 3
tan
x
=
±
3
3 3
x =
π
,
3π
2 2
2 cos x = −3 x
=
π
,
3 6
5π
,
7π
6 6
cos x
3
2 x =
π
,
2
5π
,
7π
2 2
No solution 5π
and
7π
2 2
are greater than 2π, so they are not
solutions. The solution is x =
π
.
2

2
(

(
= −
40. 3 tan 3x = 0
tan 3x = 0
3x = 0, π, 2π, 3π, 4π, 5π
43. tan2
x − 2 tan x = 0
tan x(tan x − 2) = 0
tan x = 0 or tan x − 2 = 0
x = 0,
π
,
2π
, π,
4π
,
5π
3 3 3 3
x = nπ tan x = 2
x = arctan 2 + nπ
41. cos 4x(cos x − 1) = 0 44. 2 tan2
x − 3 tan x = −1
cos 4x = 0 cos x − 1 = 0 2 tan2
x − 3 tan x + 1 = 0
4x =
π
+ 2πn,
3π
+ 2πn cos x = 1 (2 tan x − 1)(tan x − 1) = 0
2 2
2 tan x − 1 = 0 or tan x − 1 = 0
x =
π
+
π
n,
3π
+
π
n x = 0 2 tan x = 1 tan x = 1
8 2 8 2
x = 0,
π
,
3π
,
5π
,
7π
,
9π
,
11π
,
13π
,
15π
8 8 8 8 8 8 8 8
tan x =
1
2
x =
π
+ nπ
4
42. 3 csc2
5x = −4
x = arctan
1
+ nπ
csc2
5x
4
3
csc 5x = ± −
4
3
No real solution
45. tan2
θ + tan θ − 6 = 0
(tan θ + 3)(tan θ − 2) = 0
tan θ + 3 = 0 or tan θ − 2 = 0
tan θ
θ
= −3 tan θ
= arctan(−3) + nπ θ
= 2
= arctan 2 + nπ
46. sec2
x + 6 tan x + 4 = 0
1 + tan2
x + 6 tan x + 4 = 0
tan2
x + 6 tan x + 5 = 0
47. sin 75° = sin(120° − 45°)
= sin 120° cos 45° − cos120° sin 45°
3 2 1 2 
= − −

(tan x + 5)(tan x + 1) = 0
2 2  2 2
tan x + 5 = 0 or tan x + 1 = 0 =
2
4
3 + 1)
tan x = −5 tan x = −1 cos 75° = cos(120° − 45°)
x = arctan(−5) + nπ x =
3π
+ nπ = cos120° cos 45° + sin 120° sin 45°
4
= −
1 2 3 2 
+
2 2  2 2
=
2
4

3 − 1)
tan 75° = tan(120° − 45°) =
tan 120° −tan 45°
1 + tan 120° tan 45°
=
− 3 − 1
=
− 3 − 1
1 + (− 3)(1) 1 − 3
=
− 3 − 1
⋅
1 + 3
1 − 3 1 + 3
=
−4 − 2 3
−2
= 2 + 3

(
(
= − + = (
(
)
)
48. sin(375°) = sin(135° + 240°)
= sin 135° cos 240° + cos 135° sin 240°
2 1  2 3
= − + − −
2 2  2 2
=
2
3 − 1
4
cos(375°) = cos(135° + 240°)
= cos 135° cos 240° − sin 135° sin 240°
2 1 2 3
= − − − −
2 2 2 2
2
= 1 + 3
4
tan(375°) = tan(135° + 240°)
=
tan 135° +tan 240°
1 − tan 135° tan 240°
=
−1 + 3
1 − (−1)( 3)
=
−1 + 3
⋅
1 − 3
=
−4 + 2 3
= 2 − 3
1 + 3 1 − 3 1 − 3
49. sin
25π
= sin
11π
+
π
= sin
11π
cos
π
+ cos
11π
sin
π
12

6 4

6 4 6 4

1 2 3 2 2 3 − 1)
2 2  2 2 4
cos
25π
= cos
11π
+
π
= cos
11π
cos
π
− sin
11π
sin
π
12

6 4

6 4 6 4

3 2 1 2 2
= − − =
3 + 1)

2 2  2 2 4
tan
11π
+ tan
π
tan
25π
= tan
11π
+
π
= 6 4
12

6 4

1 tan
11π
tan
π
−
6 4
3 
− + 1
3

= = 2 − 3
3 
1 − − (1)3


5 3
4
−4
v
−3
5
(
=
4 4
50. sin
19π
= sin
11π
−
π 
cos
19π
= cos
11π
−
π
12

6 4

12

6 4

= sin
11π
cos
π
− cos
11π
sin
π

= cos
11π
cos
π
+ sin
11π
sin
π
6 4 6 4
1 2 3 2
6 4 6 4
3 2 1 2
= − ⋅ − ⋅ = ⋅ + −
2 2 2 2 2 2  2 2
= −
2
(1 + 3) = −
2
( 3 + 1) =
2
3 − 1)
4 4 4
tan
19π
= tan
11π
−
π
12

6 4
tan
11π
− tan
π
= 6 4
1 + tan
11π
tan
π
6 4
−
3
− 1
= 3 = − 3 − 3
⋅
3 + 3
3 
1 + − (1)
3 − 3 3 + 3
3


−(12 + 6 3)= = −2 − 3
6
51. sin 60° cos 45° − cos 60° sin 45° = sin(60° − 45°)
= sin 15°
52.
tan 68° −tan 115°
= tan(68° − 115°)
1 + tan 68° tan 115°
= tan(−47°)
y y
u x x
53. ( )
3
( 4
) 4
( 3
) 24
sin u + v = sin u cos v + cos u sin v = 5
− 5
3
+
3 3
+ 5
− 5
= − 25
54. tan(u + v) =
tan u + tan v
= 4 4 = 2 =
316 24
1 − tan u tan v
1 −
3 3

7
16
2 7 7
55. ( ) 4
( 4
) 3
( 3
)cos u − v = cos u cos v + sin u sin v =

5
− 5
+ 5
− 5
=
−1
56. ( ) 3
( 4
) 4
( 3
)sin u − v = sin u cos v − cos u sin v = 5
− 5
− 5
− 5
= 0
57. cosx +
π
= cos x cos
π
− sin x sin
π
= cos x(0) − sin x(1) = −sin x
2 2 2

, π
2

4
1 −
4
= −
=
2
= −
58. tan x −
π
= −tan
π
− x = −cot x 61. sin x +
π
− sinx −
π
= 1
2 2

4 4
59.

tan(π − x) =
tan π − tan x
= −tan x
1 − tan π tan x

2 cos x sin
π
= 1
4
60. sin(x − π ) = sin x cos π − cos x sin π
= sin x(−1) − cos x(0)
= −sin x
cos x =
2
2
x =
π
,
7π
4 4
62. cosx +
π
− cosx −
π
= 1
6 6

cos x cos
π
− sin x sin
π
− cos x cos
π
+ sin x sin
π
= 1
6 6

6 6

−2 sin x sin
π
= 1
6
63. sin u
4
< u <
3π
−2 sin x
1
= 1

sin x = −1
x =
3π
2
65. sin 4x = 2 sin 2x cos 2x
5 2 = 22 sin x cos x(cos2
x − sin2
x)
cos u = − 1 − sin2
u =
−3
5 = 4 sin x cos x(2 cos2
x − 1)
tan u =
sin u
=
4
cos u 3
= 8 cos3
x sin x − 4 cos x sin x
2
4 3 24 sin
2u = 2 sin u cos u = 2− − =
5 5 25 −2π 2π
cos 2u = cos2
u − sin2
u = −
3 2 2
− −
 7
= −
5 5 25 −2

4
2
1 − cos 2x 1 − (1 − 2 sin2
x)
tan 2u =
2 tan u
1 − tan2
u
3
= −
24
7

3
66.
1 + cos 2x
=
1 + (2 cos x2
− 1)
2 sin2
x
=
2 cos2
x
64. cos u = −
2
,
π
5 2
< u < π sin u =
1
and
5 = tan2
x
tan u
1 4
2
1 2 4 sin
2u = 2 sin u cos u = 2 − = −
5 5 5 −2π 2π

2
2 4
cos 2u = cos2
u − sin2
u = −
2  2 2
−
1
=
3 −1
5 5 5

2 sin2
3x
1 − cos 6x
2 1 − cos 6x
1
2−  67. tan 3x = 2
= =
tan 2u =
2tan u
=
2
=
−1
= −
4 cos 3x 1 + cos 6x 1 + cos 6x
1 − tan2
u 1 3 3 2
1 − − 

2 

12 
2


3
3
=
68. sin2
x cos2
x =
1 − cos 2x1 + cos 2x
2 2


1 − cos2
2x
=
4
1 −
1 + cos 4x 
= 
4
=
1 − cos 4x
8
1 − cos 150°
3 
1 − −
2 
2 + 3 1
69. sin(−75°) = − = − = − = − 2 + 3
2 2 2 2
3 
1 + −
1 + cos 150° 2  2 − 3 1
cos(−75°) = − = = = 2 − 3
2 2 2 2
3 
1 − −
− °
tan(−75°) 1 cos 150

2
= −(2 + 3) = −2 − 3
= −
sin 150°
= −
1

2 


5π 1 − −
−
5π  1 cos
6
2  2 + 3 1
70. sin = = = = 2 + 3
12  2 2 2 2

5π 1 + −
+
5π  1 cos
6
2  2 − 3 1
cos = = = = 2 − 3
12  2 2 2 2
tan
5π
=

1 − cos
5π
6
sin
5π
3 
1 − − 
= 
1 = 2 + 3
71. tan u =
4
, π
6 2
< u <
3π
(b) sin
u
=
1 − cos u
=
1 − −
3
5 4
3 2 2 2 2 5
y
2 5
=
5
1 + −
3


u cos
u 1 + cos u
= − = −
5
= −
1
−3 x 2 2 2 5
−4 5
5
= −
5
1 − −
3
(a) Because u is in Quadrant III,
u
is in Quadrant II. tan
u 1 − cos u
= =
5 = −2
2 2 sin u
−
4
5


5 3
4
1 −
1 +
1 −
,



= −
=
72. sin u =
3
, 0 < u <
π
5 2
y
u
x
(a) Because u is in Quadrant I,
u
is in Quadrant I.
2
4
(b) sin
u
=
1 − cos u
=
5
=
1
=
10
2 2 2 10 10
4
cos
u
=
1 + cos u
=
5
=
9
=
3 10
2 2 2 10 10
4
tan
u
=
1 − cos u
=
5
=
1
2 sin u 3 3
5
73. cos u
2 π
7 2
y
< u < π
7
3 5
u
x
−2
(a) Because u is in Quadrant II,
u
is in Quadrant I.
2
1 − −
2
(b) sin
u
=
1 − cos u
=
7
=
9
2 2 2 14
3 14
=
cos
u
=
14
1 + cos u
=
1 + −
2
7 5
2 2 2 14
70
=
14
1 − −
2
tan
u 1 − cos u
= =
7 3 5
=
2 sin u 3 5 5
7

1 −
1 +
1 −
= −
2 
2 
2
cos 
θ
74. tan u = −
21
,
3π
2 2
y
< u < 2π
u
2 x
5 − 21
(a) Because u is in Quadrant IV,
u
is in Quadrant II.
2
2
(b) sin
u
=
1 − cos u
=
5
=
3
=
30
2 2 2 10 10
2
cos
u
= −
1 + cos u
= −
5  = −
7
= −
70
2 2 2 10 10
2
tan
u
=
1 − cos u
=
5 3 3 21
= − = −
21
2 sin u 21
− 
21 21 7
5 
75. cos 4θ sin 6θ = 1 sin(4θ + 6θ) − sin(4θ − 6θ) = 1 sin 10θ − sin(−2θ)
76.
77.
2 sin 7θ cos 3θ
cos 6θ + cos 5θ
= 2 ⋅ 1
sin(7θ + 3θ) + sin(7θ − 3θ) = sin 10θ + sin 4θ
= 2 cos
6θ + 5θ
cos
6θ − 5θ
= 2 cos
11θ
cos
θ
2 2 2 2
78. sin 3x − sin x = 2
3x + x
sin
3x − x 79. r =
1
v0
2
sin 2θ
2 2 32
= 2 cos 2x sin x
range = 100 feet
v0 = 80 feet per second
r =
1
(80)
2
sin 2θ
32
= 100
sin 2θ
2θ
θ
= 0.5
= 30°
= 15° or
π
12
80. Volume V of the trough will be the area A of the isosceles triangle times the length l of the trough.
V =
(a)
A ⋅ l
A =
1
bh
2
cos
θ
=
h
h = 0.5 cos
θ 4 m
2 0.5 2
b b

sin
θ
= 2 b
= 0.5 sin
θ h
2 0.5 2 2 0.5 m
0.5 m
A = 0.5 sin
θ
0.5 cos
θ
= (0.5)
2
sin
θ
cos
θ
= 0.25 sin
θ
cos
θ
square meters
2 2 2 2 2 2
V = (0.25)(4) sin
θ
cos
θ
cubic meters = sin
θ
cos
θ
cubic meters
2 2 2 2
Not drawn to scale


 
=
Problem Solving for Chapter 2 281
(b) V = sin
θ
cos
θ
=
1
2 sin
θ
cos
θ
=
1
sin θ cubic meters
2 2 2

2 2 2

Volume is maximum when θ =
π
.
2
81. False. If
π
< θ < π, then
π
<
θ
<
π
, and
θ
is in
84. True. It can be verified using a product-to-sum formula.
2
Quadrant I. cos
θ
> 0
4 2 2 2
4 sin 45° cos 15° = 4 ⋅
1
[sin 60° + sin 30°]
2
2
3 1
82. True. cot x sin2
x =
cos x
sin2
x = cos x sin x.
sin x
= 2

+ =
2 2
3 + 1
85. Yes. Sample Answer. When the domain is all real
83. True. 4 sin(−x)cos(−x) = 4(−sin x) cos x
= −4 sin x cos x
numbers, the solutions of sin x =
5π
1
are x =
π
2 6
+ 2nπ
= −2(2 sin x cos x)
= −2 sin 2x
Problem Solving for Chapter 2
and x = + 2nπ , so there are infinitely many
6
solutions.
1. sin θ = ± 1 − cos2
θ You also have the following relationships:
tan θ =
sin θ
= ±
cos θ
1 − cos2
θ
cos θ
sin θ = cos
π
2
− θ 
csc θ =
1
= ±
sin θ
1
1 − cos2
θ
tan θ
csc θ
cos(π 2) − θ
cos θ
1
=
secθ
cot θ
=
1
cos θ
=
1
= ±
cos θ sec θ
cos(π 2) − θ
1
=
cos θ
tan θ 1 − cos2
θ
cot θ
cos θ
=
cos(π 2) − θ
(2n + 1)π 2nπ + π 
2. cos = cos
(12n + 1)π 1 
3. sin = sin (12nπ + π )
2 2

6 6

= cosnπ +
π 

= sin2nπ +
π
2

6
= cos nπ cos
π
− sin nπ sin
π
= sin
π
=
1
2 2
= (±1)(0) − (0)(1)
6 2
(12n + 1)π 1

= 0 So, sin
6
= for all integers n.
2

(2n + 1)π 
So, cos = 0 for all integers n.
2


4π
1 2 3 5 6

1
2
4. p(t) =
1
p (t) + 30p (t) + p (t) + p (t) + 30p (t)
1.4
1.4
p1(t) p2(t)
(a) p1(t) = sin(524πt)
1 −0.006 0.006
−0.006 0.006
p2 (t) =
p3(t) =
p5 (t) =
sin(1048πt)
2
1
sin(1572πt)
3
1
sin(2620πt)
5
1.4
p3(t)
−1.4
1.4
p5(t)
−1.4
1.4
p6
(t)
p6 (t) =
1
sin(3144πt)
6
−0.006 0.006 −0.006 0.006 −0.006 0.006
The graph of −1.4 −1.4 −1.4
p(t) =
1
sin(524πt) + 15 sin(1048πt) +
1
sin(1572πt) +
1
sin(2620πt) + 5 sin(3144πt)
4π 3 5 
yields the graph shown in the text below.
y
1.4
y = p(t)
t
0.006
(b)
−1.4
Function Period
p (t)
2π
524π
p (t)
2π
1
= ≈ 0.0038
262
=
1
≈ 0.0019
(c) 1.4 Max
0 0.00382
p3(t)
1048π
2π
524
=
1
≈ 0.0013
−1.4 Min
1
1572π
2π
786
1
Over one cycle, 0 ≤ t < , you have five t-intercepts:
262
p5(t)
p6(t)
2620π
2π
3144π
= ≈ 0.0008
1310
1
= ≈ 0.0006
1572
t = 0, t ≈ 0.00096, t ≈ 0.00191, t ≈ 0.00285,
t ≈ 0.00382
(d) The absolute maximum value of p over one cycle is
p ≈ 1.1952, and the absolute minimum value
The graph of p appears to be periodic with a
period of
1
≈ 0.0038.
262
of p over one cycle is p ≈ −1.1952.


2
2
= −
b
5. From the figure, it appears that u + v = w. Assume that u, v, and w are all in Quadrant I.
From the figure:
tan u =
s
=
1
3s 3
tan v =
s
=
1
2s 2
tan w =
s
= 1
s
tan u + v
tan u + tan v 1 3 + 1 2 5 6
= = = = 1 = tan w.
( )
1 − tan u tan v
1 − (1 3)(1 2) 1 − (1 6)
So, tan(u + v) = tan w. Because u, v, and w are all in Quadrant I, you have
arctantan(u + v) = arctan[tan w]u + v = w.
6. y = −
16
x2
+ (tan θ)x + h0
Let h0
v0
2
cos2
θ
= 0 and take half of the horizontal distance:
1 1
v sin 2θ =
1
v 2 sin θ cos θ
1
= v sin θ cos θ
2
2 32
0
0 ( ) 0
2
64 32
Substitute this expression for x in the model.
2
y = −
16 1
v 2
sin θ cos θ
 sin θ 1 
+ v sin θ cos θ
v 2
cos2
θ 32
0
cos θ 32
0
0 
1
v 2
sin2
θ +
1
v 2
sin2
θ
64
0
1
= v0
2
sin2
θ
64
32
0
7. (a)
10 θ 10
h
sin
θ
b
1
b
= 2
1
2
and cos
θ
=
h
2 10 2 10
b = 20 sin
θ
h = 10 cos
θ
2 2
A =
1
bh
2
1 θ θ 
= 20 sin 10 cos
2 2 2

2
(b)

= 100 sin
θ
cos
θ
2 2
θ θ 
A = 502 sin cos
2 2
θ 
= 50 sin 2


= 50 sin θ
Because sin
π
= 1 is a maximum, θ =
π
.So, the area is a maximum at A = 50 sin
π
= 50 square meters.
2 2 2


2
8. The hypotenuse of the larger right triangle is:
θ
2
1 2(1 + cosθ )
1
sin2
θ + (1 + cos θ)
2
=
=
sin2
θ + 1 + 2 cos θ + cos2
θ
2 + 2 cos θ
cos θ θ = 2(1 + cos θ)
sin θ
sin
θ
=
sin θ
=
sin θ
⋅
1 − cos θ
=
sin θ 1 − cos θ
=
sin θ 1 − cos θ
=
1 − cos θ
2 
θ 
2(1 + cos θ)
1 + cos θ
2(1 + cos θ)
(1 + cos θ)
2
1 − cos θ
1 + cos θ
2(1 − cos2
θ) 2 sin θ 2
cos = = =
2  2(1 + cos θ) 2(1 + cos θ) 2
tan
θ
=
sin θ
1 + cos θ
9. F
0.6W sin(θ + 90°)=
sin 12°
(a) F =
0.6W(sin θ cos 90° +cos θ sin 90°)
sin 12°
=
0.6W (sin θ)(0) + (cos θ)(1)
sin 12°
(b) Let y1 =
550
0.6(185) cos x
.
sin 12°
=
0.6W cos θ
sin 12° 0 90
0
(c) The force is maximum (533.88 pounds) when θ = 0°.
The force is minimum (0 pounds) when θ = 90°.
π(t + 0.2)
10. Seward: D = 12.2 − 6.4 cos
11. d = 35 − 28 cos
π
t when t = 0 corresponds to
182.6  6.2

π(t + 0.2)
New Orleans: D = 12.2 − 1.9 cos
12:00 A.M.
(a) The high tides occur when cos
π
t = −1. Solving
182.6  6.2
(a)

20
0 365
0
yields t = 6.2 or t = 18.6.
These t-values correspond to 6:12 A.M. and 6:36 P.M.
The low tide occurs when cos
π
t = 1. Solving
6.2
yields t = 0 and t = 12.4 which corresponds to
12:00 A.M. and 12:24 P.M.
(b) The graphs intersect when t ≈ 91 and when
t ≈ 274. These values correspond to April 1 and
(b) The water depth is never 3.5 feet. At low tide, the
depth is d = 35 − 28 = 7 feet.
October 1, the spring equinox and the fall equinox.
(c) Seward has the greater variation in the number of
daylight hours. This is determined by the
a
m
p
litudes, 6.4 and
1.9.

(d) Period:
2π
= 365.2 days
π 182.6
(c)
70
0 24
0

4π
2 2 2 2 
2

2 2 2 
2
2

.
12. h1 = 3.75 sin 733t + 7.5 θ α
sin +

h = 3.75 sin 733 t + + 7.5 13. (a) n =
2 2
2
3 θ
(a) 15
sin
2
sin
θ
cos
α
+ cos
θ
sin
α 
= 
sin
θ 
0 1
0
(b) The period for h1 and h2 is
2π
733
≈ 0.0086.
= cos
α
+ cot
θ
sin
α 

θ
12 For α = 60°, n = cos 30° + cot sin 30°
2
n =
3
+
1
cot
θ
0 2π
733
3
2 2
(b) For glass, n = 1.50.
3 1


θ
The graphs intersect twice per cycle. 1.50 = +
2 2
cot 
2
There are
1
≈ 116.66 cycles in the interval 3 θ
2π 733 21.50 − = cot
[0, 1], so the graphs intersect approximately
2  2
233.3 times.
1 θ 
= tan
3 − 3
θ


= 2 tan−1 1
3 − 3


θ ≈ 76.5°
14. (a)
(b)
sin(u + v + w) = sin(u + v) + w
= sin(u + v) cos w + cos(u + v) sin w
= [sin u cos v + cos u sin v] cos w + [cos u cos v − sin u sin v] sin w
= sin u cos v cos w + cos u sin v cos w + cos u cos v sin w − sin u sin v sin w
tan(u + v + w) = tan(u + v) + w
tan(u + v) + tan w
=
1 − tan(u + v) tan w
tan u + tan v
+ tan w
=
1 − tan u tan v
⋅
(1 − tan u tan v)
tan u + tan v 
1 − tan w
1 − tan u tan v
(1 − tan u tan v)
tan u + tan v + (1 − tan u tan v) tan w
=
(1 − tan u tan v) − (tan u + tan v) tan w
=
tan u + tan v + tan w − tan u tan v tan w
1 − tan u tan v − tan u tan w − tan v tan w

6 6 3 3
=
1 cos 2x +
1 cos 2x
4
2
4 
.
2
2

2
15. (a) Let y1 = sin x and y2 = 0.5. (b) Let y1 = cos x and y2 = −0.5.
2
0 2π
2
0 2π
−2
sin x ≥ 0.5 on the interval
π
,
5π 
−2
cos x ≤ −0.5 on the interval
2π
,
4π
.
(c) Let y1 = tan x and y2


= sin x. (d) Let y1 = cos x and y2


= sin x.
2
0 2π
2
0 2π
−2 −2

π

5π
tan x < sin x on the intervals
π
, π and
3π
, 2π . cos x ≥ sin x on the intervals 0, and , 2π .
2

2

4

4

16. (a) f (x) = sin4
x + cos4
x
= (sin2
x) + (cos2
x)
2
−  
2
+ 
2 2 
=
1
(1 − 2 cos 2x + cos2
2x) + (1 + 2 cos 2x + cos2
2x)
=
1
(2 + 2 cos2
2x)
=
1
(1 + cos2
2x)
1 cos 4x
= 1 +
2 2 
=
1
(3 + cos 4x)
4
(b) f (x) = sin4
x + cos4
x
= (sin2
x) + cos4
x
2
2
4
= (1 − cos x) + cos x
(c)
= 1 − 2 cos2
2x + cos4
x + cos4
x
= 2 cos4
x − 2 cos2
x + 1
f (x) = sin4
x + cos4
x
= sin4
x + 2 sin2
x cos2
x + cos4
x − 2 sin2
x cos2
x

2
= (sin
2
x + cos2
x) − 2 sin2
x cos2
x
= 1 − 2 sin2
x cos2
x

2
( 2
)
(d) f (x) = 1 − 2 sin2
x cos2
x
1 − cos 2x1 + cos 2x
= 1 − 2
2 2


= 1 −
1
(1 − cos2
2x)
1 1
= + cos2
2x
2 2
1 1
= + 1 − sin 2x
2 2
= 1 −
1
sin2
2x
2
(e) No; there is often more than one way to rewrite a trigonometric expression, so your result and your friend’s result
could both be correct.

= <
Practice Test for Chapter 2
1. Find the value of the other five trigonometric functions, given tan x 4 , sec x 0.11
2. Simplify
sec2
x + csc2
x
.csc2
x(1 + tan2
x)
3. Rewrite as a single logarithm and simplify ln tan θ − ln cot θ .
4. True or false:
cos
π
− x =
1
2

csc x
5. Factor and simplify: sin4
x + (sin2
x) cos2
x
6. Multiply and simplify: (csc x + 1)(csc x − 1)
7. Rationalize the denominator and simplify:
cos2
x
1 − sin x
8. Verify:
1 + cos θ
sin θ
sin θ
+ = 2 csc θ
1 + cos θ
9. Verify:
tan4
x + 2 tan2
x + 1 = sec4
x
10. Use the sum or difference formulas to determine:
(a) sin 105°
(b) tan 15°
11. Simplify: (sin 42°) cos 38° − (cos 42°) sin 38°
12. Verify tan +
π
=
1 + tan θ
.θ
4  1 − tan θ
13. Write sin(arcsin x − arccos x) as an algebraic expression in x.
14. Use the double-angle formulas to determine:
(a) cos 120°
(b) tan 300°
15. Use the half-angle formulas to determine:
(a) sin 22.5°
(b) tan
π
12
16. Given sin θ = 4 5, θ lies in Quadrant II, find cos(θ 2).

1
Practice Test for Chapter 2 289
17. Use the power-reducing identities to write (sin2
x) cos2
x in terms of the first power of cosine.
18. Rewrite as a sum: 6(sin 5θ) cos 2θ.
19. Rewrite as a product: sin(x + π ) + sin(x − π ).
20. Verify
sin 9x + sin 5x
cos 9x − cos 5x
= −cot 2x.
21. Verify:
(cos u) sin v = 2
sin(u + v) − sin(u − v).
22. Find all solutions in the interval [0, 2π ):
4 sin2
x = 1
tan2
θ + ( 3 − 1) tan θ − 3 = 0
sin 2x = cos x
25. Use the quadratic formula to find all solutions in the interval [0, 2π ):
tan2
x − 6 tan x + 4 = 0

2.1 Using Fundamental Identities

Objectives
Recognize and write the fundamental
trigonometric identities.
Use the fundamental trigonometric identities to
evaluate trigonometric functions, simplify
trigonometric expressions, and rewrite
trigonometric expressions.
3

Introduction
You will learn how to use the fundamental identities to do
the following.
1. Evaluate trigonometric functions.
2. Simplify trigonometric expressions.
3. Develop additional trigonometric identities.
4. Solve trigonometric equations.
5

Introduction
Pythagorean identities are sometimes used in radical form
such as
or
where the sign depends on the choice of u.
8

Using the Fundamental Identities
9

10
One common application of trigonometric identities is to
use given values of trigonometric functions to evaluate
other trigonometric functions.

11
Example 1 – Using Identities to Evaluate a Function
Use the values and tan u > 0 to find the values of
all six trigonometric functions.
Solution:
Using a reciprocal identity, you have
.
Using a Pythagorean identity, you have
Pythagorean identity

12
Example 1 – Solution cont’d
Substitute for cos u.
. Simplify.
Because sec u < 0 and tan u > 0, it follows that u lies in
Quadrant III.
Moreover, because sin u is negative when u is in
Quadrant III, choose the negative root and obtain

13
Example 1 – Solution
Knowing the values of the sine and cosine enables you to
find the values of all six trigonometric functions.
cont’d

14

15
Example 2 – Simplifying a Trigonometric Expression
Simplify
sin x cos2 x – sin x.
Solution:
First factor out a common monomial factor and then use a
fundamental identity.
sin x cos2 x – sin x = sin x(cos2 x – 1)
= –sin x(1 – cos2 x)
= –sin x(sin2 x)
= –sin3 x
Factor out common
monomial factor.
Factor out –1.
Multiply.

16
When factoring trigonometric expressions, it is helpful to
find a special polynomial factoring form that fits the
expression.
On occasion, factoring or simplifying can best be done by
first rewriting the expression in terms of just one
trigonometric function or in terms of sine and cosine only.

17
Example 7 – Rewriting a Trigonometric Expression
Rewrite so that it is not in fractional form.
Solution:
From the Pythagorean identity
cos2 x = 1 – sin2 x = (1 – sin x)(1 + sin x)
multiplying both the numerator and the denominator by
(1 – sin x) will produce a monomial denominator.
Multiply numerator and
denominator by (1 – sin x).
Multiply.

18
Write as separate fractions.
Product of fractions
Reciprocal and quotient
identities

2.2
Verifying Trigonometric
Identities

Objective
Verify trigonometric identities.
3

5
Introduction
In this section, you will study techniques for verifying
Remember that a conditional equation is an equation that is
true for only some of the values in its domain.
For example, the conditional equation
sinx = 0
is true only for
x = nπ
Conditional equation
where n is an integer. When you find these values, you are
solving the equation.

6
Introduction
On the other hand, an equation that is true for all real
values in the domain of the variable is an identity. For
example, the familiar equation
sin2x = 1 – cos2x Identity
is true for all real numbers x. So, it is an identity.

Verifying Trigonometric Identities
7

8
Although there are similarities, verifying that a trigonometric
equation is an identity is quite different from solving an
equation. There is no well-defined set of rules to follow in
verifying trigonometric identities, and it is best to learn the
process by practicing.

9
Verifying trigonometric identities is a useful process when
you need to convert a trigonometric expression into a form
that is more useful algebraically.
When you verify an identity, you cannot assume that the
two sides of the equation are equal because you are trying
to verify that they are equal.
As a result, when verifying identities, you cannot use
operations such as adding the same quantity to each side
of the equation or cross multiplication.

10
Example 1 – Verifying a Trigonometric Identity
Verify the identity
Solution:
Start with the left side because it is more complicated.
Simplify.
Reciprocal identity
Quotient identity

11
Simplify.
Notice that you verify the identity by starting with the left
side of the equation (the more complicated side) and using
the fundamental trigonometric identities to simplify it until
you obtain the right side.

2.3
Solving Trigonometric
Equations

Objectives
Use standard algebraic techniques to solve
trigonometric equations.
Solve trigonometric equations of quadratic type.
Solve trigonometric equations involving multiple
angles.
Use inverse trigonometric functions to solve
trigonometric equations.
3

5
Introduction
To solve a trigonometric equation, use standard algebraic
techniques (when possible) such as collecting like terms
and factoring.
Your preliminary goal in solving a trigonometric equation is
to isolate the trigonometric function on one side of the
equation.
For example, to solve the equation 2 sin x = 1, divide each
side by 2 to obtain

6
Introduction
To solve for x, note in the figure below that the equation
has solutions x = π/6 and x = 5π/6 in the interval
[0, 2π).

7
Introduction
Moreover, because sin x has a period of 2π, there are
infinitely many other solutions, which can be written as
and General solution
where n is an integer, as shown above.

8
Introduction
The figure below illustrates another way to show that the
equation has infinitely many solutions.
Any angles that are coterminal with π/6 or 5π/6 will also be
solutions of the equation.
When solving trigonometric
equations, you should write
your answer(s) using exact
values rather than decimal
approximations.

9
Example 1 – Collecting Like Terms
Solve
Solution:
Begin by isolating sin x on one side of the equation.
Write original equation.
Add sin x to each side.
Subtract from each side.

10
Combine like terms.
Divide each side by 2.
Because sin x has a period of 2π, first find all solutions in
the interval [0, 2π).
These solutions are x = 5π/4 and x = 7π/4. Finally, add
multiples of 2π to each of these solutions to obtain the
general form
where n is an integer.

Equations of Quadratic Type
11

12
Equations of Quadratic Type
Many trigonometric equations are of quadratic type
ax2 + bx + c = 0, as shown below.
Quadratic in sin x Quadratic in sec x
2 sin2 x – sin x – 1 = 0 sec2 x – 3 sec x – 2 = 0
2(sin x)2 – sin x – 1 = 0 (sec x)2 – 3(sec x) – 2 = 0
To solve equations of this type, factor the quadratic or,
when this is not possible, use the Quadratic Formula.

13
Example 4 – Factoring an Equation of Quadratic Type
Find all solutions of 2 sin2 x – sin x – 1 = 0 in the interval
[0, 2π).
Solution:
Treat the equation as a quadratic in sin x and factor.
2 sin2 x – sin x – 1 = 0
(2 sin x + 1)(sin x – 1) = 0
Factor.

14
Setting each factor equal to zero, you obtain the following
solutions in the interval [0, 2π).
2 sin x + 1 = 0 and sin x – 1 = 0
cont’d

Functions Involving Multiple Angles
15

16
Functions Involving Multiple Angles
The next example involve trigonometric functions of
multiple angles of the forms cos ku and tan ku.
To solve equations of these forms, first solve the equation
for ku, and then divide your result by k.

17
Example 7 – Solving a Multiple-Angle Equation
Solve 2 cos 3t – 1 = 0.
Solution:
2 cos 3t – 1 = 0
2 cos 3t = 1
Add 1 to each side.

18
In the interval [0, 2π), you know that 3t = π/3 and 3t = 5π/3
are the only solutions, so, in general, you have
and
Dividing these results by 3, you obtain the general solution

20
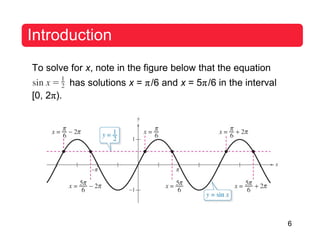
Example 9 – Using Inverse Functions
sec2 x – 2 tan x = 4
1 + tan2 x – 2 tan x – 4 = 0
tan2 x – 2 tan x – 3 = 0
(tan x – 3)(tan x + 1) = 0
Original equation
Combine like terms.
Factor.
Setting each factor equal to zero, you obtain two solutions
in the interval (–π/2, π/2). [We know that the range of the
inverse tangent function is (–π/2, π/2).]
x = arctan 3 and

21
Example 9 – Using Inverse Functionscont’d
Finally, because tan x has a period of π, you add multiples
of π to obtain
x = arctan 3 + nπ and
General solution
You can use a calculator to approximate the value of
arctan 3.

2.4 Sum and Difference Formulas

3
Objective
Use sum and difference formulas to evaluate
trigonometric functions, verify identities, and
solve trigonometric equations.

4
Using Sum and Difference
Formulas

5
Using Sum and Difference Formulas
In this and the following section, you will study the uses of
several trigonometric identities and formulas.
Example 1 shows how sum and difference formulas can
enable you to find exact values of trigonometric functions
involving sums or differences of special angles.

6
Example 1 – Evaluating a Trigonometric Function
Find the exact value of .
Solution:
To find the exact value of sin π /12, use the fact that
Consequently, the formula for sin(u – v) yields

7
Try checking this result on your calculator. You will find that
sin π /12 ≈ 0.259.

8
Example 5 – Proving a Cofunction identity
Use a difference formula to prove the cofunction identity
= sin x.
Solution:
Using the formula for cos(u – v), you have

9
Using Sum and Difference Formulas
Sum and difference formulas can be used to rewrite
expressions such as
and , where n is an integer
as expressions involving only sin θ or cos θ.
The resulting formulas are called reduction formulas.

10
Example 7 – Solving a Trigonometric Equation
Find all solutions of
in the interval .
Solution:
Algebraic Solution
Using sum and difference formulas, rewrite the equation as

11
So, the only solutions in the interval [0, 2π) are x = 5π /4
and x = 7π /4.
cont’d

2.5
Multiple-Angle and
Product-to-Sum Formulas

3
Objectives
Use multiple-angle formulas to rewrite and
evaluate trigonometric functions.
Use power-reducing formulas to rewrite and
evaluate trigonometric functions.
Use half-angle formulas to rewrite and evaluate
trigonometric functions.

4
Objectives
Use product-to-sum and sum-to-product
formulas to rewrite and evaluate trigonometric
functions.
Use trigonometric formulas to rewrite real-life
models.

6
Multiple-Angle Formulas
In this section, you will study four other categories of
1. The first category involves functions of multiple angles
such as sin ku and cos ku.
2. The second category involves squares of trigonometric
functions such as sin2 u.
3. The third category involves functions of half-angles such
as sin(u/2).
4. The fourth category involves products of trigonometric
functions such as sin u cos v.

7
Multiple-Angle Formulas
You should learn the double-angle formulas because
they are used often in trigonometry and calculus.

8
Example 1 – Solving a Multiple-Angle Equation
Solve 2 cos x + sin 2x = 0.
Solution:
Begin by rewriting the equation so that it involves functions
of x (rather than 2x). Then factor and solve.
2 cos x + sin 2x = 0
2 cos x + 2 sin x cos x = 0
2 cos x(1 + sin x) = 0
2 cos x = 0 and 1 + sin x = 0
Double-angle formula.
Factor.
Set factors equal to zero.

9
So, the general solution is
and
Solutions in [0, 2π)
where n is an integer. Try verifying these solutions
graphically.

11
Power-Reducing Formulas
The double-angle formulas can be used to obtain the
following power-reducing formulas.

12
Example 4 – Reducing a Power
Rewrite sin4 x in terms of first powers of the cosines of
multiple angles.
Solution:
Note the repeated use of power-reducing formulas.
Property of exponents
Power-reducing formula
Expand.

13
Power-reducing formula
Distributive Property
Simplify.
Factor out common factor.

14
You can use a graphing utility to check this result, as
shown below. Notice that the graphs coincide.
cont’d

16
Half-Angle Formulas
You can derive some useful alternative forms of the
power-reducing formulas by replacing u with u/2. The
results are called half-angle formulas.

17
Example 5 – Using a Half-Angle Formula
Find the exact value of sin 105°.
Solution:
Begin by noting that 105° is half of 210°. Then, using the
half-angle formula for sin(u/2) and the fact that 105° lies in
Quadrant II, you have

18
.
cont’d
The positive square root is chosen because sin θ is positive
in Quadrant II.

20
Each of the following product-to-sum formulas can be
verified using the sum and difference formulas.
Product-to-sum formulas are used in calculus to solve
problems involving the products of sines and cosines of two
different angles.

21
Example 7 – Writing Products as Sums
Rewrite the product cos 5x sin 4x as a sum or difference.
Solution:
Using the appropriate product-to-sum formula, you obtain
cos 5x sin 4x = [sin(5x + 4x) – sin(5x – 4x)]
= sin 9x – sin x.

22
Occasionally, it is useful to reverse the procedure and write
a sum of trigonometric functions as a product. This can be
accomplished with the following sum-to-product
formulas.

24
Example 10 – Projectile Motion
Ignoring air resistance, the range of a projectile fired at an
angle θ with the horizontal and with an initial velocity of
v0 feet per second is given by
where r is the horizontal distance (in feet) that the projectile
travels.

25
Example 10 – Projectile Motion
A football player can kick a football
from ground level with an initial
velocity of 80 feet per second
a. Write the projectile motion model in a simpler form.
b. At what angle must the player kick the football so that
the football travels 200 feet?
cont’d

26
2
a. You can use a double-angle formula to rewrite the
projectile motion model as
r = v0
2 (2 sin θ cos θ)
= v0
2 sin 2θ.
Rewrite original projectile motion model.
Rewrite model using a double-angle formula.
b. r = v0 sin 2θ Write projectile motion model.
200 = (80)2 sin 2θ Substitute 200 for r and 80 for v0.

27
200 = 200 sin 2θ
1 = sin 2θ
Simplify.
You know that 2θ = π/2, so dividing this result by 2
produces θ = π/4.
Because π/4 = 45°, the player must kick the football at
an angle of 45° so that the football travels 200 feet.

28
Trigonometry 10th Edition Larson SOLUTIONS MANUAL
Full download:
https://testbanklive.com/download/trigonometry-10th-edition-larson-solutions-manual/
People also search:
algebra and trigonometry ron larson 9th edition pdf
trigonometry larson 9th edition pdf
algebra and trigonometry ron larson pdf
ron larson trigonometry 9th edition pdf
trigonometry 10th edition solutions pdf-
algebra & trigonometry
algebra and trigonometry 10th edition pdf
algebra and trigonometry 10th edition free

Trigonometry 10th edition larson solutions manual

More Related Content

What's hot

Similar to Trigonometry 10th edition larson solutions manual

Recently uploaded

Trigonometry 10th edition larson solutions manual