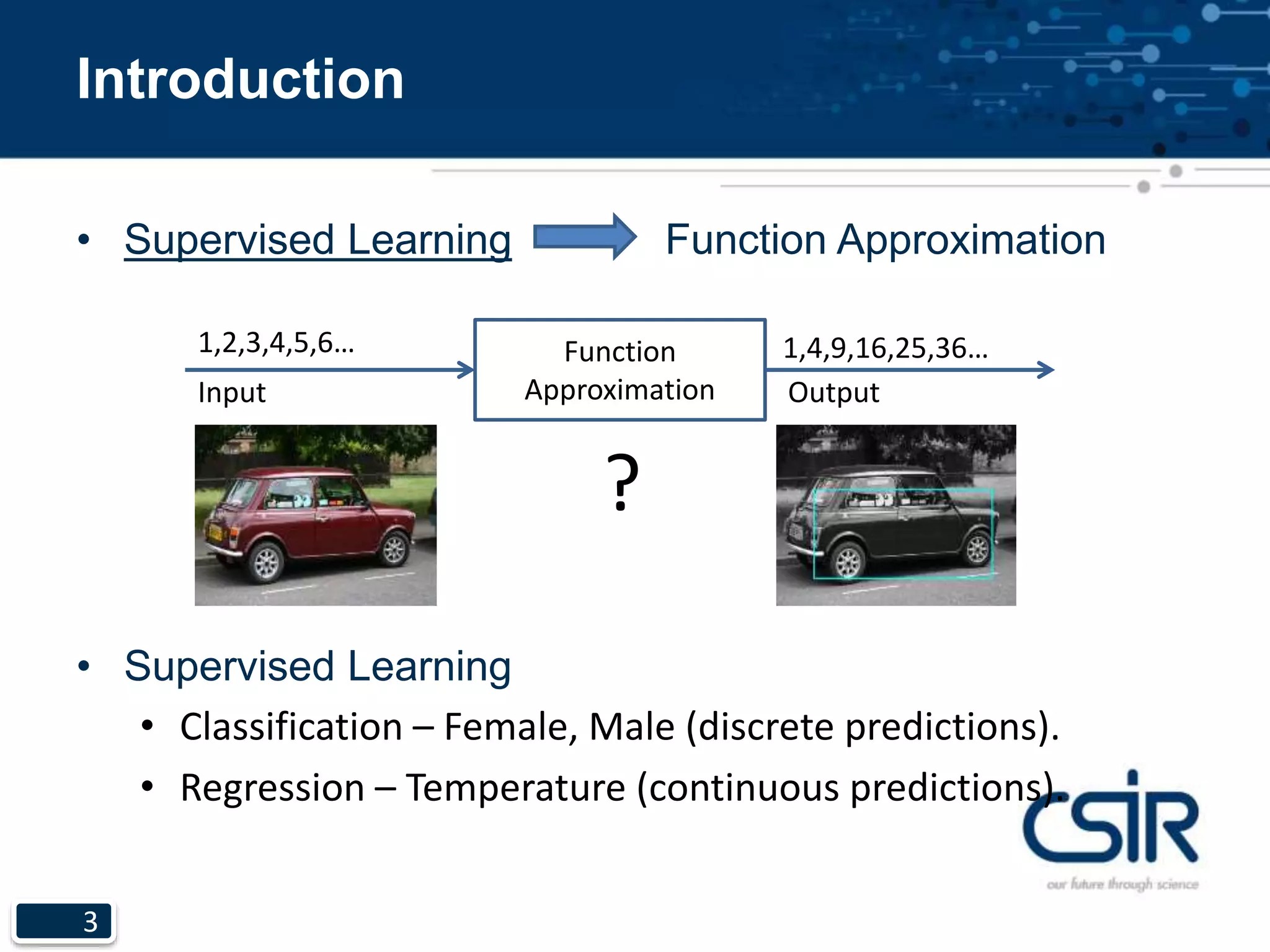
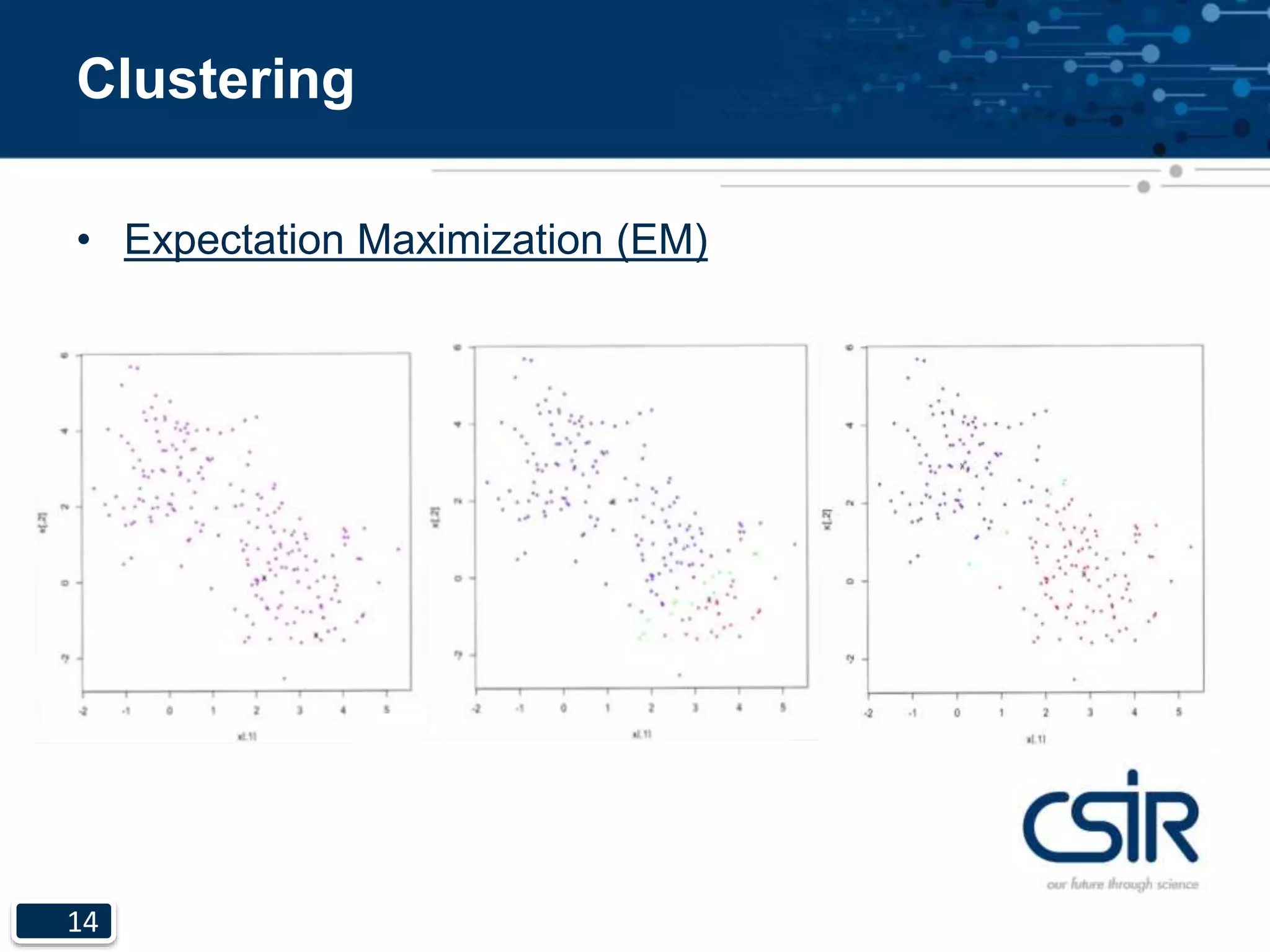
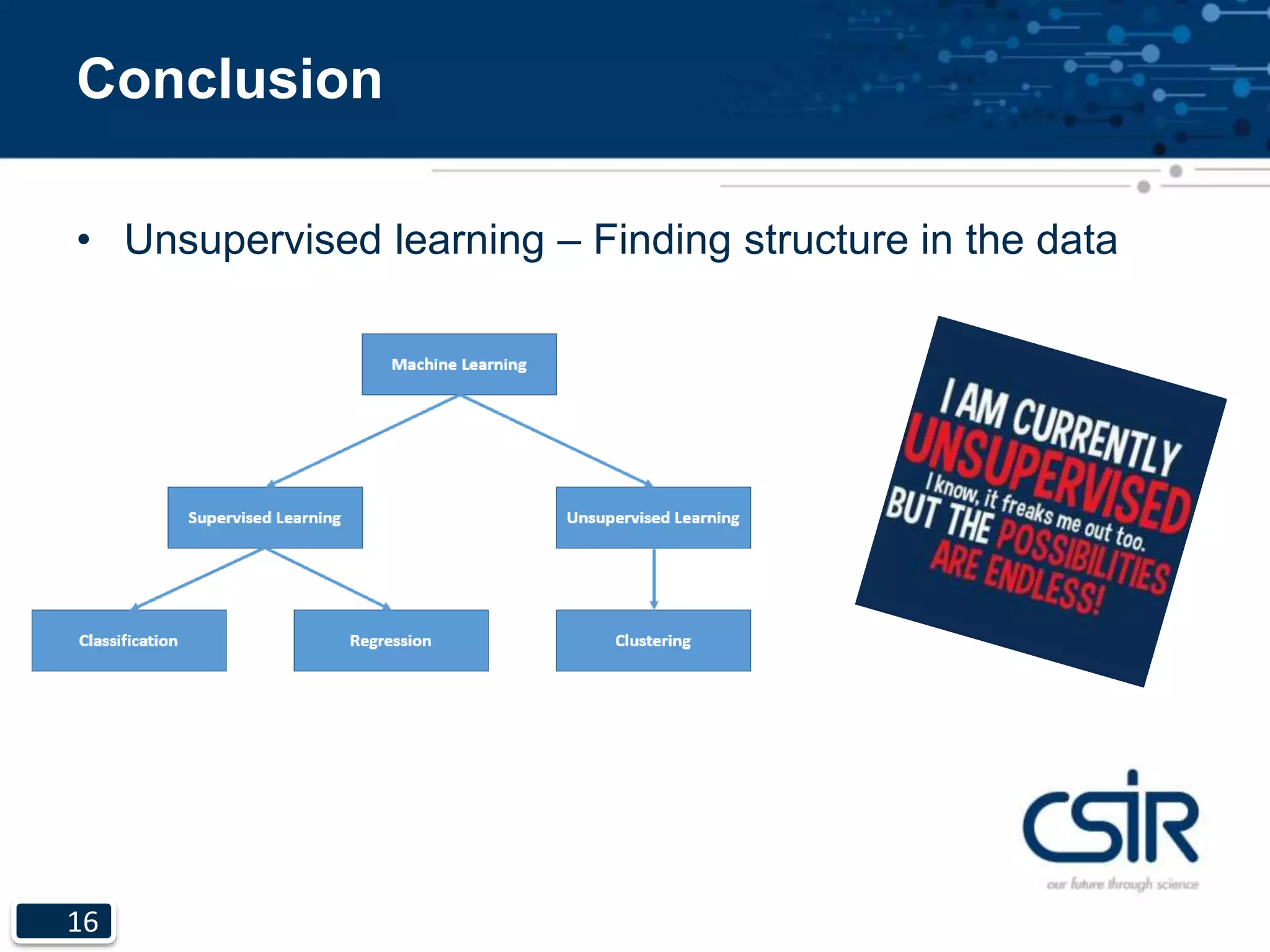
This document provides an overview of unsupervised learning and clustering algorithms. It introduces clustering as the task of grouping objects such that objects within the same group are more similar to each other than objects in other groups. It describes single linkage clustering, k-means clustering, and expectation maximization algorithms. It also discusses properties of clustering, noting that no algorithm can achieve richness, scale-invariance, and consistency simultaneously.

1. Contents
Unsupervised Learning
Beatrice van Eden
Machine Learning Reading group
Introductory Theme

2. 2
Contents
 Introduction
 Unsupervised Learning concepts
 Clustering the idea
 Basic clustering problem
 Algorithms
 Single linkage clustering (SLC)
 Issues with SLC
 K-means clustering
 K-means in Euclidean space
 K-means as optimization
 Soft clustering
 Expectation Maximization (EM)
 Clustering properties and impossibilities
Charles Isbell Michael Littman
Andrew Ng
https://www.coursera.org/learn/machine-learning/home/info
https://www.udacity.com/course/machine-learning-
supervised-learning--ud675

3. 3
Introduction
• Supervised Learning Function Approximation
• Supervised Learning
• Classification – Female, Male (discrete predictions).
• Regression – Temperature (continuous predictions).
Function
Approximation
1,2,3,4,5,6… 1,4,9,16,25,36…
Input Output
?

4. 4
Why Unsupervised Learning?
• Unsupervised Learning Pre-processing
• Try to find hidden structure
Finding Structure
Function
Approximation
Pixels Summaries Labels
UL SL

5. 5
Introduction
• Optimization
• SL - Label data well
• UL - Cluster scores well
• Data is important
• Algorithms are important

6. 6
Clustering
• Clustering is the task of grouping a set of objects in
such a way that objects in the same group are more
similar to each other than to those in other
groups/clusters.

7. 7
Clustering
• Basic clustering problem
• Given: set of objects 𝑋
Inter-object distances D(X, Y) = 𝐷 𝑌, 𝑋 , 𝑋, 𝑌𝜖𝑋
• Output: Partition 𝑃 𝐷(𝑋) = 𝑃 𝐷(𝑌) if 𝑋 and 𝑌 in same
cluster
• Extreme clustering algorithm: ∀ 𝑋 𝑃 𝐷(𝑋) = 1, ∀ 𝑋 𝑃 𝐷(𝑋) = X
(Humans), (Each Unique)

8. 8
Clustering
• Single linkage clustering (SLC)
• Consider each object a cluster (n objects)
• Define inter cluster distance as the distance between
the closest two points in the two clusters
• Merge two closest clusters
• Repeat n-k times to make n clusters.
1 6542 3

9. 9
Clustering
• Issues with SLC
K=2
X

10. 10
Clustering
• K-means clustering
• Pick k “centres” (at random)
• Each centre “claims” its closest points
• Recompute the centre by averaging the clustered
points
• Repeat until convergence (does it always converge and
give good answers)

11. 11
Clustering
• K-means in Euclidean space
• 𝐴 = 𝑃 𝑡 𝑋 : Partition/Cluster of objects 𝑋
• 𝐶𝑖 : Set of all points in cluster 𝑖 = 𝑋 𝑠. 𝑡. 𝑃 𝑋 = 𝑖
• 𝐶𝑒𝑛𝑡𝑒𝑟𝑖 = 𝑦𝜖𝐶𝑖
𝑦
𝐶 𝑖
• 𝐶𝑒𝑛𝑡𝑒𝑟𝑖 → 𝑃 𝑡 = 𝑎𝑟𝑔𝑚𝑖𝑛 𝑋𝐶𝑒𝑛𝑡𝑒𝑟𝑖
2
𝐶𝑒𝑛𝑡𝑒𝑟𝑖 =
𝑦𝜖𝐶𝑖
𝑦
𝐶 𝑖
t
t
t
t t-1
2
t
t

12. 12
Clustering
• K-means as optimization
• Configurations: Centre / Partition
• Scores: 𝐸(𝑃, 𝐶𝑒𝑛𝑡𝑒𝑟) = 𝑋 𝐶𝑒𝑛𝑡𝑒𝑟 𝑃 𝑋 − 𝑋
2
• Neighbourhood: 𝑃, 𝐶𝑒𝑛𝑡𝑒𝑟 = 𝑃1, 𝐶𝑒𝑛𝑡𝑒𝑟 ∪ 𝑃, 𝐶𝑒𝑛𝑡𝑒𝑟1
• Optimisation
• Hillclimbing, Genetic algorithms, Simulated Annealing
2

13. 13
Clustering
• Soft clustering
• If k=2 what happens to d?
• Can d be shared between clusters?
• Assume the data was generated by
– Select one of k Gaussians distributions, know the variance,
sampled from uniformly
– Sample Xi from that Gaussian
– Repeat n times
• Task: find a hypothesis h=<µ1,...,µk> (means of distribution)
that maximizes the probability of the data

14. 14
Clustering
• Expectation Maximization (EM)

15. 15
Clustering
• Clustering properties
• Richness: For any assignment of objects to clusters there is
some distance matrix D such that PD returns that cluster
• Scale-invariance: Scaling distances by a positive value does
not change the clustering
• Consistency: Shrinking intra cluster distances and
expanding inter cluster distances does not change the
cluster
• Impossibility theorem
• No clustering algorithm can achieve all three properties

16. 16
Conclusion
• Unsupervised learning – Finding structure in the data

17. Thank you
Name (email@csir.co.za)