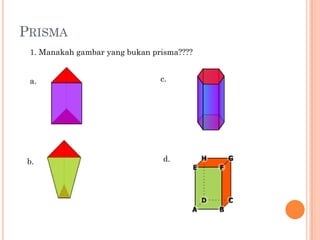
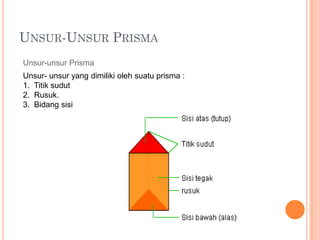
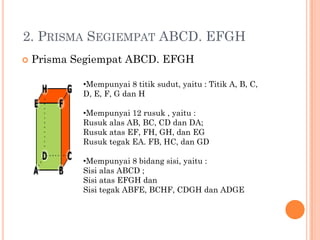
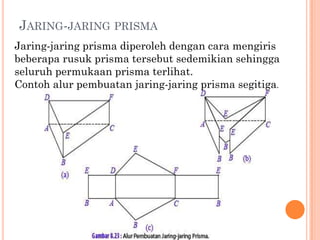
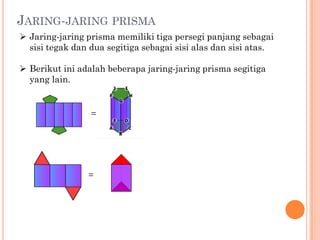
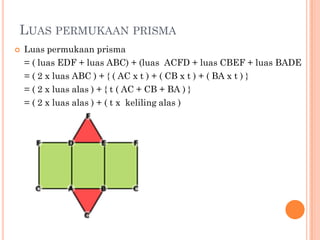
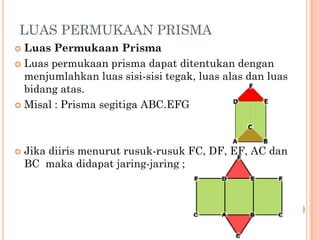
Dokumen ini menjelaskan tentang prisma, termasuk definisi, sifat-sifat, unsur-unsur, serta contoh prisma segitiga, segiempat, dan segilima. Luas permukaan dan volume prisma dapat dihitung menggunakan rumus yang bergantung pada bentuk alas dan tinggi prisma. Selain itu, dokumen juga memberikan contoh soal yang menunjukkan penerapan rumus dalam menghitung luas permukaan dan volume prisma.

1. Nama anggota :
 Nathalyn Christine
 Ruth Friskilla
 Wendy Iman Yakinur
 Robby Pangestu

2. PRISMA
 Prisma adalah bangun ruang yang dibatasi oleh
dua bidang berhadapan yang sama dan
sebangun atau (kongruen) dan sejajar, serta
bidang-bidang lain yang berpotongan menurut
rusuk-rusuk yang sejajar.
 Prisma diberi nama berdasarkan bentuk segi-n
pada bidang alas atau bidang atasnya.

3. PRISMA
1. Manakah gambar yang bukan prisma????
a. c.
b. d.

4. PRISMA
2. Mengapa dikatakan gambar di bawah ini bukan
prisma?
Jawabannya:
Bukan merupakan prisma karena
bidang atas dan bidang bawah
tidak kongruen

5. UNSUR-UNSUR PRISMA
Unsur-unsur Prisma
Unsur- unsur yang dimiliki oleh suatu prisma :
1. Titik sudut
2. Rusuk.
3. Bidang sisi

6. 1. PRISMA SEGITIGA ABC.DEF
 Prisma Segitiga ABC.DEF
•Mempunyai 6 titik sudut, yaitu : Titik A, B, C,
D, E, dan F
•Mempunyai 9 rusuk , yaitu :
Rusuk alas AB, BC, dan AC;
Rusuk atas DE, EF, dan DF
Rusuk tegak AD. BE, dan CF
•Mempunyai 5 bidang sisi, yaitu :
Sisi alas ABC ;
sisi atas DEF dan
Sisi tegak ABED, BCFE dan ACFD

7. 2. PRISMA SEGIEMPAT ABCD. EFGH
 Prisma Segiempat ABCD. EFGH
•Mempunyai 8 titik sudut, yaitu : Titik A, B, C,
D, E, F, G dan H
•Mempunyai 12 rusuk , yaitu :
Rusuk alas AB, BC, CD dan DA;
Rusuk atas EF, FH, GH, dan EG
Rusuk tegak EA. FB, HC, dan GD
•Mempunyai 8 bidang sisi, yaitu :
Sisi alas ABCD ;
Sisi atas EFGH dan
Sisi tegak ABFE, BCHF, CDGH dan ADGE

8. 3. PRISMA SEGILIMA ABCDE.FGHIJ
 Prisma Segilima ABCDE.FGHIJ
•Mempunyai 10 titik sudut, yaitu :
Titik A, B, C, D, E, F, G, H, I, dan J
•Mempunyai 15 rusuk , yaitu :
Rusuk alas AB, BC, CD, DE dan EA
Rusuk atas FG, GH, HI, IJ dan JF
Rusuk tegak FA. GH, HI, IJ dan JE
•Mempunyai 7 bidang sisi, yaitu :
Sisi alas ABCDE ;
sisi atas FGHIJ
Sisi tegak ABGF, BCHG, CDIH, DEJI, dan AEJF

9. PERTANYAAN
 Prisma Segienam ABCDEF.GHIJKL punya
berapa rusuk ?
a. 14 rusuk
Penjelasan
b. 16 rusuk •Mempunyai 18 rusuk , yaitu :
Rusuk alas AB, BC, CD, DE, EF dan FA ;
c. 18 rusuk Rusuk atas GH, HI, IJ, JK, KL dan LG
Rusuk tegak GA. HB, IC, JD, KE dan LF
d. 20 rusuk

10.  Sifat-sifat prisma:
a) Dua bidang kongruen dan sejajar disebut bidang
alas dan bidang atas,
b) Rusuk-rusuk tegaknya saling sejajar,
c) Bidang-bidang tegaknya berbentuk persegi
panjang,
d) Bidang diagonalnya berbentuk persegi panjang,
e) Nama prisma bergantung bentuk alasnya.

11. BIDANG DIAGONAL PRISMA
 Pada prisma segienam, terdapat 2 buah diagonal
bidang yang sejajar yaitu BI dan FK.
 Kedua diagonal bidang tersebut beserta ruas
garis KI dan FB membentuk suatu bidang di
dalam prisma segienam ABCDEF.GHIJKL.
Bidang tersebut adalah bidang BFKI yang
merupakan bidang diagonal prisma segienam.

12. JARING-JARING PRISMA
Jaring-jaring prisma diperoleh dengan cara mengiris
beberapa rusuk prisma tersebut sedemikian sehingga
seluruh permukaan prisma terlihat.
Contoh alur pembuatan jaring-jaring prisma segitiga.

13. JARING-JARING PRISMA
 Jaring-jaring prisma memiliki tiga persegi panjang sebagai
sisi tegak dan dua segitiga sebagai sisi alas dan sisi atas.
 Berikut ini adalah beberapa jaring-jaring prisma segitiga
yang lain.
=
=

14. LUAS PERMUKAAN PRISMA
 Luas permukaan prisma
= ( luas EDF + luas ABC) + (luas ACFD + luas CBEF + luas BADE
= ( 2 x luas ABC ) + { ( AC x t ) + ( CB x t ) + ( BA x t ) }
= ( 2 x luas alas ) + { t ( AC + CB + BA ) }
= ( 2 x luas alas ) + ( t x keliling alas )

15.  Luas Permukaan Prisma
 Luas permukaan prisma dapat ditentukan dengan
menjumlahkan luas sisi-sisi tegak, luas alas dan luas
bidang atas.
 Misal : Prisma segitiga ABC.EFG
 Jika diiris menurut rusuk-rusuk FC, DF, EF, AC dan
BC maka didapat jaring-jaring ;

16. LUAS PERMUKAAN PRISMA
 Luas permukaan prisma
= luas alas + luas bidang atas +luas bidang-bidang tegak
= luas alas + luas alas + (a x t + b x t + c x t)
= (2 x luas alas) + (a + b + c) x t
= (2 x luas alas) + (keliling alas x tinggi)
 Jadi, untuk setiap prisma (tegak) berlaku rumus berikut.
Luas permukaan prisma (tegak)
= (2 x luas alas) + (keliling alas x tinggi)

17. LUAS PERMUKAAN PRISMA
 Contoh soal:
 Hitunglah luas permukaan prisma segitiga
dengan alas berbentuk segitiga siku-siku
berukuran 3cm, 4cm, 5cm dan tinggi prisma 10
cm !
 Jawab:
 Sisi alas; a = 3 cm
t = 4 cm
 Luas alas = x a x t
= x 3 x 4 = 6 cm2
 Keliling alas = 3 cm + 4 cm + 5 cm
= 12 cm

18. LUAS PERMUKAAN PRISMA
 Luas permukaan prisma
= ( 2 x luas alas ) + ( keliling alas x tinggi )
= (2 x 6 cm2 ) + ( 12 cm x 10 cm )
= 12 cm2 + 120 cm2
= 132 cm2
 Jadi luas permukaan prisma 132 cm2

19. LUAS PERMUKAAN PRISMA
 Pertanyaan :
 Sebuah prisma tingginya 20 cm dengan alas
segitiga siku-siku sisinya 3 cm dan 4 cm. Maka
luas prisma adalah…..
a. 60 cm2
b. 120 cm2
c. 240 cm2
d. 252 cm2

20. LUAS PERMUKAAN PRISMA
 Luas alas = x a x t
= x 3 x 4 = 6 cm2
 Untuk mencari alas digunakan rumus
phytagoras:
2 2
c= 3 4
= 9 16
= 25
= 5 (kel. alas)
Luas prisma=(2 x luas alas) + (Keliling alas x tinggi)
Luas prisma=(2 x 6) +(12 x 20)
=12 +240
=252 cm2

21. VOLUM PRISMA
 Jika balok pada Gambar 1(i) dipotong tegak
sepanjang salah satu bidang diagonalnya, maka akan
terbentuk dua prisma segitiga seperti Gambar 1(ii).
Kedua prisma segitiga pada Gambar 1(ii) dapat
digabungkan kembali sehingga terbentuk sebuah
prisma segitiga seperti Gambar 1(iii).

22. VOLUM PRISMA
 Dengan demikian, prisma pada Gambar 1 (iii)
dan balok pada Gambar 1 (i) memiliki volume
yang sama, luas alas yang sama, dan tinggi yang
sama pula, sehingga dapat dinyatakan sebagai
berikut.
 Volume Prisma segitiga = volume balok
= luas alas balok x tinggi balok
= luas alas prisma x tinggi prisma
Volume prisma = luas alas x tinggi
atau
V = Lt

23. VOLUME PRISMA
 Untuk menentukan volume prisma yang alasnya
bukan berbentuk segitiga, dapat dilakukan
dengan cara membagi prisma tersebut menjadi
beberapa prisma segitiga seperti pada Gambar 2
berikut.

24. VOLUME PRISMA
 Gambar 2(i) adalah prisma segienam beraturan. Untuk
menentukan volumenya, prisma tersebut dibagi menjadi 6
buah prisma segitiga yang sama dan sebangun seperti
ditunjukkan pada Gambar 2(ii) dan 2(iii), sehingga
 Volume Prisma Segienam = 6 x volume prisma segitiga
= 6 x luas segitiga alas x tinggi
= (6 x luas segitiga alas) x tinggi
= luas segienam x tinggi
= luas alas x tinggi
 Kesimpulannya:
Volume prisma = luas alas x tinggi
atau
V = Lt

25. VOLUME PRISMA
 Pertanyaan:
Hitunglah volum prisma segilima jika luas
alasnya 50 cm2 dan tinggi 15 cm !
 Jawab :
Luas alas = 50 cm2
t = 15 cm
 Volum prisma = luas alas x tinggi
= 50 cm2 x 15 cm
= 750 cm3
 Jadi volum prisma segilima 750 cm3