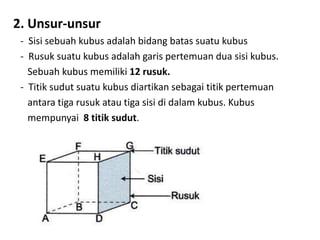
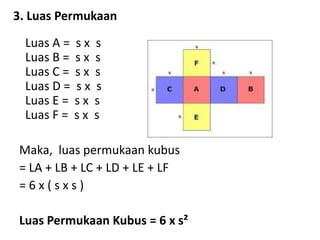
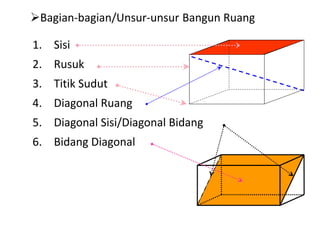
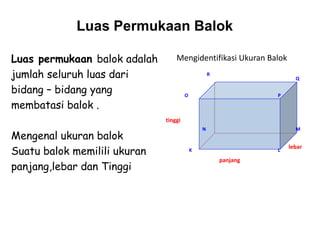
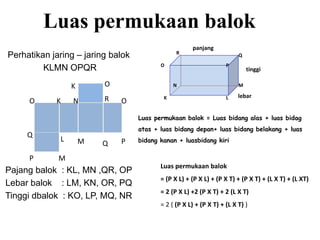
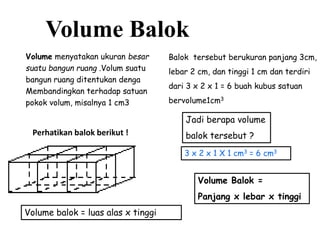
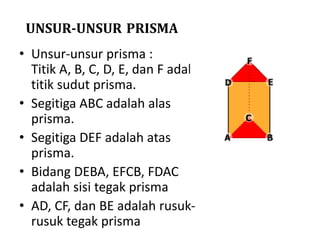
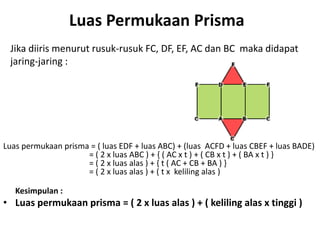
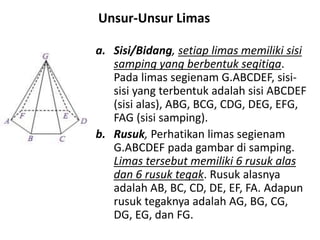
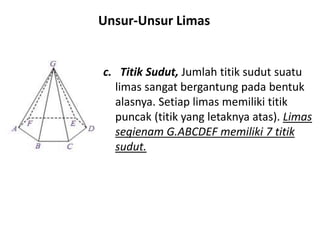
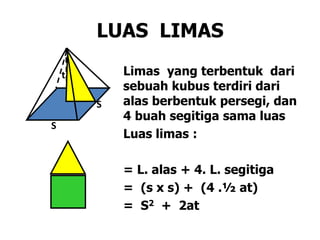
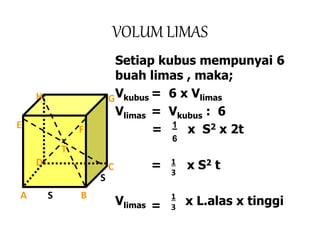
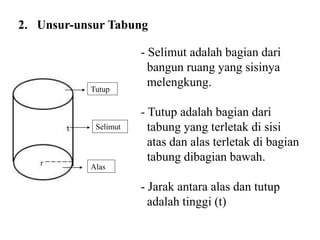
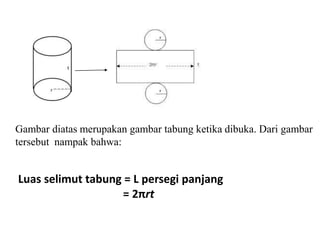
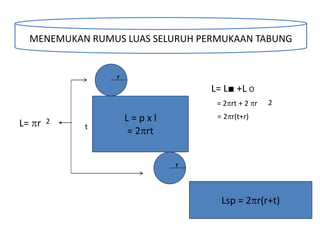
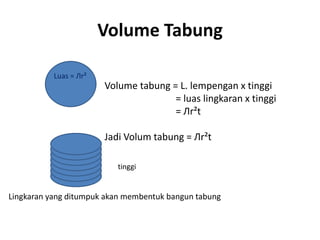
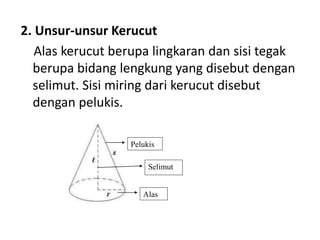
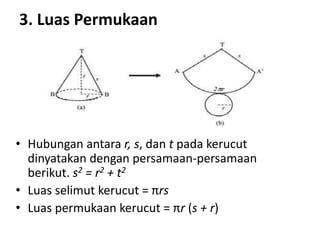
Dokumen ini membahas berbagai jenis bangun ruang, termasuk kubus, balok, prisma, limas, tabung, kerucut, dan bola. Masing-masing bangun dijelaskan dengan pengertian, unsur-unsur, rumus luas permukaan, dan volum. Kesimpulan merangkum rumus-rumus penting untuk menghitung luas dan volume berbagai bangun ruang.

1. BANGUN RUANG
KELOMPOK 9 :
LANNI INTAN .P (292011282)
TIKA LARASWATI (292011290)
YOSEPH AGUNG (292011298)

2. Pengertian
Bangun ruang merupakan bangun matematika
yang memiliki isi atau volume. Bisa juga
disebut bagian ruang yang dibatasi oleh
himpunaan titik-titik yang terdapat pada
seluruh permukaan bangun tersebut.
Permukaan bangun itu disebut sisi.

3. I. Bangun Ruang Sisi Datar
A. Kubus
1. Pengertian
Kubus adalah sebuah benda ruang yang dibatasi
oleh enam (bidang) datar yang masing-masing
berbentuk persegi yang sama dan sebangun atau
kongruen.

4. 2. Unsur-unsur
- Sisi sebuah kubus adalah bidang batas suatu kubus
- Rusuk suatu kubus adalah garis pertemuan dua sisi kubus.
Sebuah kubus memiliki 12 rusuk.
- Titik sudut suatu kubus diartikan sebagai titik pertemuan
antara tiga rusuk atau tiga sisi di dalam kubus. Kubus
mempunyai 8 titik sudut.

5. 3. Luas Permukaan
Luas A = s x s
Luas B = s x s
Luas C = s x s
Luas D = s x s
Luas E = s x s
Luas F = s x s
Maka, luas permukaan kubus
= LA + LB + LC + LD + LE + LF
= 6 x ( s x s )
Luas Permukaan Kubus = 6 x s²

6. 4. Volume KUBUS
• Kubus ABCD dengan panjang rusuk s satuan
• Luas Alas ABCD = sisi x sisi
= s x s
= s2
• Volum Kubus = Luas Alas ABCD x tinggi
= s2 x s
= s3
Volum Kubus dengan panjang sisi s satuan
adalah s3 satuan volum.

7. B. Balok
Balok adalah sebuah benda ruang yang
dibatasi oleh enam (bidang) datar yang
masing-masing berbentuk persegi panjang.

8. Bagian-bagian/Unsur-unsur Bangun Ruang
1. Sisi
2. Rusuk
3. Titik Sudut
4. Diagonal Ruang
5. Diagonal Sisi/Diagonal Bidang
6. Bidang Diagonal

9. Luas Permukaan Balok
Luas permukaan balok adalah
jumlah seluruh luas dari
bidang – bidang yang
membatasi balok .
Mengenal ukuran balok
Suatu balok memilili ukuran
panjang,lebar dan Tinggi
panjang
tinggi
lebar
O
K L
MN
P
Q
R
Mengidentifikasi Ukuran Balok

10. Luas permukaan balok
Perhatikan jaring – jaring balok
KLMN OPQR
Pajang balok : KL, MN ,QR, OP
Lebar balok : LM, KN, OR, PQ
Tinggi dbalok : KO, LP, MQ, NR
OK
K
L M
N O
PQ
R
M
O
Q
P
Luas permukaan balok = Luas bidang alas + luas bidag
atas + luas bidang depan+ luas bidang belakang + luas
bidang kanan + luasbidang kiri
O
K L
MN
P
QR
panjang
tinggi
lebar
Luas permukaan balok
= (P X L) + (P X L) + (P X T) + (P X T) + (L X T) + (L XT)
= 2 (P X L) +2 (P X T) + 2 (L X T)
= 2 ( (P X L) + (P X T) + (L X T) )

11. Volume Balok
Volume menyatakan ukuran besar
suatu bangun ruang .Volum suatu
bangun ruang ditentukan denga
Membandingkan terhadap satuan
pokok volum, misalnya 1 cm3
Perhatikan balok berikut !
Balok tersebut berukuran panjang 3cm,
lebar 2 cm, dan tinggi 1 cm dan terdiri
dari 3 x 2 x 1 = 6 buah kubus satuan
bervolume1cm3
Jadi berapa volume
balok tersebut ?
3 x 2 x 1 X 1 cm3 = 6 cm3
Volume Balok =
Panjang x lebar x tinggi
Volume balok = luas alas x tinggi

12. c. PRISMA
prisma adalah bangun ruang yang dibatasi
oleh dua bidang berhadapan yang sama dan
sebangun atau kongruen dan sejajar, serta
bidang - bidang lain yang berpotongan
menurut rusuk - rusuk yang sejajar.

13. UNSUR-UNSUR PRISMA
• Unsur-unsur prisma :
Titik A, B, C, D, E, dan F adalah
titik sudut prisma.
• Segitiga ABC adalah alas
prisma.
• Segitiga DEF adalah atas
prisma.
• Bidang DEBA, EFCB, FDAC
adalah sisi tegak prisma
• AD, CF, dan BE adalah rusuk-
rusuk tegak prisma

14. Jika diiris menurut rusuk-rusuk FC, DF, EF, AC dan BC maka didapat
jaring-jaring :
Luas permukaan prisma = ( luas EDF + luas ABC) + (luas ACFD + luas CBEF + luas BADE)
= ( 2 x luas ABC ) + { ( AC x t ) + ( CB x t ) + ( BA x t ) }
= ( 2 x luas alas ) + { t ( AC + CB + BA ) }
= ( 2 x luas alas ) + ( t x keliling alas )
Kesimpulan :
• Luas permukaan prisma = ( 2 x luas alas ) + ( keliling alas x tinggi )
Luas Permukaan Prisma

15. • Volum limas dapat ditentukan dengan membelah
sebuah balok menjadi dua bagian sama besar melalui
salah satu diagonal bidang sehingga membentuk dua
prisma yang kongruen.
2 Volum prisma = volume balok
= p x l x t
Volum prisma = ½ x p x l x t
Volum prisma = (1/2 x luas alas balok) x t
Volum prisma = luas alas prisma x t
Volum prisma = luas alas x tinggi
Kesimpulan :
Volum Prisma = luas alas x tinggi

16. D. LIMAS
Limas adalah bangun ruang yang
alasnya berbentuk segi banyak
(segitiga, segi empat, segi lima atau
segi-n) dan bidang/sisi tegaknya
berbentuk segitiga yang berpotongan
pada satu titik. Titik potong dari sisi-
sisi tegak limas disebut Titik puncak
limas.

17. a. Sisi/Bidang, setiap limas memiliki sisi
samping yang berbentuk segitiga.
Pada limas segienam G.ABCDEF, sisi-
sisi yang terbentuk adalah sisi ABCDEF
(sisi alas), ABG, BCG, CDG, DEG, EFG,
FAG (sisi samping).
b. Rusuk, Perhatikan limas segienam
G.ABCDEF pada gambar di samping.
Limas tersebut memiliki 6 rusuk alas
dan 6 rusuk tegak. Rusuk alasnya
adalah AB, BC, CD, DE, EF, FA. Adapun
rusuk tegaknya adalah AG, BG, CG,
DG, EG, dan FG.
Unsur-Unsur Limas

18. c. Titik Sudut, Jumlah titik sudut suatu
limas sangat bergantung pada bentuk
alasnya. Setiap limas memiliki titik
puncak (titik yang letaknya atas). Limas
segienam G.ABCDEF memiliki 7 titik
sudut.
Unsur-Unsur Limas

19. LUAS LIMAS
Limas yang terbentuk dari
sebuah kubus terdiri dari
alas berbentuk persegi, dan
4 buah segitiga sama luas
Luas limas :
= L. alas + 4. L. segitiga
= (s x s) + (4 .½ at)
= S2 + 2at
S
S
t

20. VOLUM LIMAS
Setiap kubus mempunyai 6
buah limas , maka;
Vkubus = 6 x Vlimas
Vlimas = Vkubus : 6
= x S2 x 2t
= x S2 t
Vlimas = x L.alas x tinggi
A
H
E F
D C
B
G
T
S
S
1
6
1
3
1
3

21. II. Bangun Ruang sisi Lengkung
A. Tabung
1. Pengertian tabung
Tabung atau silinder adalah bangun ruang tiga
dimensi yang dibentuk oleh dua buah lingkaran
identik yang sejajar dan sebuah persegi panjang yang
mengelilingi kedua lingkaran tersebut. Sehingga
jaring-jaring tabung terdiri dari dua buah lingkaran
dan sebuah persegi panjang.

22. Tutup
Selimut
Alas
2. Unsur-unsur Tabung
- Selimut adalah bagian dari
bangun ruang yang sisinya
melengkung.
- Tutup adalah bagian dari
tabung yang terletak di sisi
atas dan alas terletak di bagian
tabung dibagian bawah.
- Jarak antara alas dan tutup
adalah tinggi (t)

23. Gambar diatas merupakan gambar tabung ketika dibuka. Dari gambar
tersebut nampak bahwa:
Luas selimut tabung = L persegi panjang
= 2πrt

24. MENEMUKAN RUMUS LUAS SELURUH PERMUKAAN TABUNG
L = p x l
= 2rt
r
r
tL= r 2
L= L■ +L Ο
2
Lsp = 2r(r+t)
= 2r(t+r)
= 2rt + 2 r

25. Volume Tabung
Luas = Лr²
Lingkaran yang ditumpuk akan membentuk bangun tabung
Volume tabung = L. lempengan x tinggi
= luas lingkaran x tinggi
= Лr²t
Jadi Volum tabung = Лr²t
tinggi

26. t
r
r
r
MENEMUKAN RUMUS VOLUME TABUNG
• Potonglah tabung menjadi 12 bagian seperti gambar diatas
• Susun hingga membentuk prisma

27. Volume Tabung =
Volume Prisma =
Jadi Volume Tabung = Лr²t
Lalas x tinggi
Lalas x tinggi
= r.r x t
= Лr²t

28. B. Kerucut
1. Pengertian kerucut
Kerucut adalah suatu bangun ruang yang
dibatasi oleh sebuah daerah lingkaran dan
sebuah bidang lengkung yang simetris terhadap
porosnya yang melalui titik pusat lingkaran
tersebut.

29. 2. Unsur-unsur Kerucut
Alas kerucut berupa lingkaran dan sisi tegak
berupa bidang lengkung yang disebut dengan
selimut. Sisi miring dari kerucut disebut
dengan pelukis.
Alas
Pelukis
Selimut

30. 3. Luas Permukaan
• Hubungan antara r, s, dan t pada kerucut
dinyatakan dengan persamaan-persamaan
berikut. s2 = r2 + t2
• Luas selimut kerucut = πrs
• Luas permukaan kerucut = πr (s + r)

31. Sediakan wadah yang berbentuk tabung & kerucut yang
mempunyai jari-jari dan tinggi yang sama
Isilah kerucut dengan air sampai penuh, kemudian tuangkan pada
pada tabung!! Lihat Percobaannya
Jadi Tabung tersebut terisi penuh dengan 3 kali menuang air
dengan menggunakan wadah kerucut

32. Dari kegiatan tersebut dapat disimpulkan:
Volume Tabung = 3 x Volume Kerucut
r2t = 3 x Volume Kerucut
1/3 r2t = Volume Kerucut

33. 4. Volume Kerucut
Volume: 1/3 π r2 t
r = jari-jari lingkaran alas
s = panjang garis pelukis kerucut
t = tinggi kerucut

34. c. BOLA
1. Bola adalah bangun ruang tiga dimensi yang
dibentuk oleh tak hingga lingkaran berjari-jari
sama panjang dan berpusat pada satu titik yang
sama. Bola hanya memiliki 1 sisi.

35. Luas Bola
Perhatikan gambar berikut
r

36. Luas Bola
Luas Bola = 4x luas lingkaran
= 4Лr²
Kulit jeruk dikupas dan tempelkan di lingkaran yang
diameternya sama dengan diameter belahan jeruk

37. Sediakan wadah yang berbentuk setengah Bola & Kerucut yang
mempunyai jari-jari dan tinggi yang sama
Isilah kerucut dengan air sampai penuh, kemudian tuangkan pada
setengah bola!!
Lihat Percobaannya
Jadi Setengah bola tersebut terisi penuh dengan 2 kali
menuang air dengan menggunakan wadah kerucut

38. Kesimpulan:
Volum ½ Bola = 2 x volum kerucut
= 2 x 1/3 Лr² t
= 2/3 Лr² t
= 2/3 Лr³ →( t=r )
Volum Bola = 2 x Volum ½ bola
= 2 x 2/3 Лr³
= 4/3 Лr³
Jadi Volum bola = 4/3 Лr³