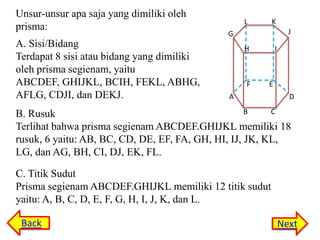
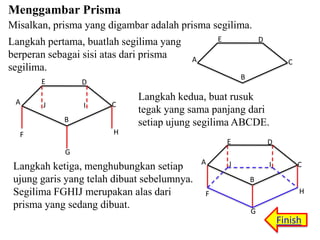
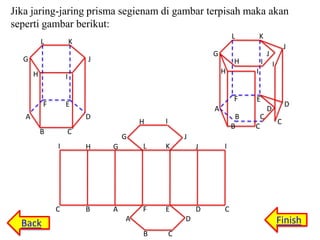
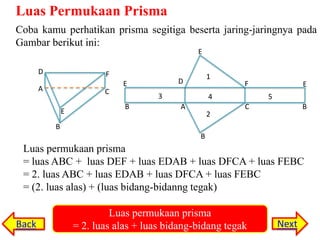
Prisma adalah bangun ruang yang memiliki sifat alas dan atap yang sama bentuknya serta sisi samping berbentuk persegi panjang. Prisma memiliki unsur seperti sisi, rusuk, titik sudut, diagonal bidang, dan bidang diagonal. Luas permukaan dan volume prisma dapat dihitung dengan rumus luas permukaan = 2 x luas alas + luas bidang tegak dan volume = luas alas x tinggi.

1. MULAI

2. Bangun Ruang Sisi
Datar
Penulis
Materi
Pembahasan
Profil
Contoh soal
Kesimpulan
Evaluasi
Klik table berwarna kuning untuk melanjutkan ke materi yang ingin di lihat.

3. Pengertian
Sifat
Prisma
Menggambar
Jaring Prisma
Luas
Permukaan
Klik table berwarna kuning untuk melanjutkan ke materi yang ingin di lihat.
Back

4. Prisma
Pengertian Prisma
Berbeda dengan kubus dan balok, bangun ruang ini memiliki
kekhasan tersendiri. Coba perhatikan bangun ruang tersebut
memiliki bentuk alas dan atap yang sama bentuk dan aturannya.
Selain itu, semua sisi bagian samping berbentuk persegipanjang
bangun ruang ini dinamakan prisma.
L
F
G
C
J
I
H
E
D
F
B
A
K
E
A
D
B
C
Finish

5. Sifat-Sifat Prisma
F
C
Sifat-sifat prisma adalah sebagai berikut:
E
D
a. Prisma memiliki bentuk alas dan atap
yang kongruen.
B
A
b. Setiap sisi bagian samping prisma berbentuk persegipanjang.
c. Prisma memiliki rusuk tegak.
d. Setiap diagonal bidang pada sisi yang sama memiliki ukuran yang
sama.
Back
Next

6. Unsur-unsur apa saja yang dimiliki oleh
prisma:
A. Sisi/Bidang
Terdapat 8 sisi atau bidang yang dimiliki
oleh prisma segienam, yaitu
ABCDEF, GHIJKL, BCIH, FEKL, ABHG,
AFLG, CDJI, dan DEKJ.
L
K
J
G
H
F
I
E
A
D
B
C
B. Rusuk
Terlihat bahwa prisma segienam ABCDEF.GHIJKL memiliki 18
rusuk, 6 yaitu: AB, BC, CD, DE, EF, FA, GH, HI, IJ, JK, KL,
LG, dan AG, BH, CI, DJ, EK, FL.
C. Titik Sudut
Prisma segienam ABCDEF.GHIJKL memiliki 12 titik sudut
yaitu: A, B, C, D, E, F, G, H, I, J, K, dan L.
Back
Next

7. L
K
J
G
H
F
I
E
A
D
B
D. Diagonal Bidang
Prisma segienam ABCDEF. GHIJKL pada
gambar disamping . BG disebut sebagai
diagonal bidang pada bidang prisma
segienam ABCDEF.
C
L
E. Bidang Diagonal
Prisma segienam ABCDEF.GHIJKL gambar
disamping. Terdapat dua buah diagonal
bidang yaitu BI dan FK dengan KI dan FB
membentuk suatu bidang di dalam prisma
segienam ABCDEF.GHIJKL.
Back
K
J
G
H
F
I
E
A
D
B
C
Finish

8. Menggambar Prisma
Misalkan, prisma yang digambar adalah prisma segilima.
Langkah pertama, buatlah segilima yang
berperan sebagai sisi atas dari prisma
segilima.
E
A
E
D
A
C
B
D
J
I
C
B
Langkah kedua, buat rusuk
tegak yang sama panjang dari
setiap ujung segilima ABCDE.
H
F
E
D
J
I
G
Langkah ketiga, menghubungkan setiap
ujung garis yang telah dibuat sebelumnya.
Segilima FGHIJ merupakan alas dari
prisma yang sedang dibuat.
A
C
B
H
F
G
Finish

9. Jaring-jaring Prisma
Jaring-jaring prisma diperoleh dengan cara mengiris beberapa rusuk
prisma tersebut sedemikian sehingga seluruh permukaan prisma terlihat.
J
D
C
E
D
F
A
I
F
E
A
L
B
(a)
J
H
C
B
(b)
I
F
E
A
D
B
Back
G
K
G
H
C
(c)
Next

10. JARING-JARING PRISMA SEGITIGA
Yang pertama prisma yang akan dibuat jaring-jaringnya adalah
prisma segitiga. Berikut ini adalah alur pembuatan jaring-jaring
prisma segitiga.
Back
Next

11. Jika jaring-jaring prisma segitiga di gambar terpisah maka akan
seperti gambar berikut:
D
F
A
D
C
F
A
C
E
B
E
E E
B
B B
E
E
D
F
E
B
A
C
B
B
Back
Next

12. JARING-JARING PRISMA SEGILIMA
Back
Next

13. Jika jaring-jaring prisma segilima di gambar terpisah maka akan
seperti gambar berikut:
J
F
A
I
E
D
J
H
F E
F
G
C
A A
B
I
DH
G
G
B
C
H
C
G
B
B
G
F
G
B
H
J
A
I
E
F
D
A
H
G
C
B
C
Next
Back
B

14. JARING-JARING PRISMA SEGIENAM
Back
Next

15. Jika jaring-jaring prisma segienam dimaka akan seperti gambar berikut: akan
Jika jaring-jaring prisma segitiga di gambar terpisah gambar terpisah maka
seperti gambar berikut:
L
L
K
G
G
J
H
F
A
D
B
H
C
B
B
I
G
I
E
C
C
D
D
C
J
I
H
G
L
K
J
I
C
Back
I
J
J
I
F
E
A
H
H
I
K
B
A
F
E
D
C
A
D
B
C
Finish

16. Luas Permukaan Prisma
Coba kamu perhatikan prisma segitiga beserta jaring-jaringnya pada
Gambar berikut ini:
E
D
F
A
C
E
1
D
E
3
B
F
4
A
2
E
5
C
B
B
B
Luas permukaan prisma
= luas ABC + luas DEF + luas EDAB + luas DFCA + luas FEBC
= 2. luas ABC + luas EDAB + luas DFCA + luas FEBC
= (2. luas alas) + (luas bidang-bidanng tegak)
Back
Luas permukaan prisma
= 2. luas alas + luas bidang-bidang tegak
Next

17. Volume Prisma
G
H
E
H
F
H
E
G
F
F
t
D
A
P
l
B
t
D
C
H
E
A
P
D
C
B
B
l
F
D
A
P
B
Dengan demikian, volume prisma segitiga adalah setengah kali
volume balok.
Back
Next

18. Volume prisma BCD.FGH
= ½ x volume balok ABCD.EFGH
= ½ x ( p x l x t)
= (½ x p x l) x t
= luas alas x tinggi
Back
Volume prisma = luas alas x tinggi
Finish

19. Contoh soal:
1. Dari gambar prisma segitiga
disamping, tentukan:
a. Sisi
d. Diagonal bidang
b. Rusuk
e. Bidang diagonal
c. Titik sudut
L
J
I
F
E
D
A
B
Back
F
A
C
E
B
K
G
H
D
2. Perhatikan gambar prisma segienam
disamping, tentukan:
a. Panjang diagonal bidang CH
b. Luas bidang diagonal CELH.
C
Next

20. S
3. Perhatikan prisma segitiga siku-siku
pada gambar di samping. Tentukan:
a. Luas permukaan prisma keseluruhan!
b. Luas permukaan prisma tanpa tutup!
U
8 cm
P
10 cm
6 cm
T
R
7 cm
Q
F
4. Perhatikan prisma segitiga pada
C
gambar di samping. Dari gambar
3 cm
tersebut tentukan:
a. Luas alas prisma segitiga
A
b. Volume prisma segitiga
Back
5 cm
E
D
9 cm
4 cm
B
Next

21. Jawab:
1.
a.
b.
c.
d.
e.
Dari prisma segitiga ABC.DEF, diperoleh:
sisi bidang: ABC, DEF, ABED, BCFE dan ACFD
rusuk: AB, BC, CA, DE, EF, FD, AD, BE, dan CF
titik sudut: A, B, C, D, E dan F
diagonal bidang: AE, BD, BF, CE, AF dan DC
bidang diagonal: ABF, BCD, ACE, AEF, BDF dan CDE
2. a. Panjang diagonal CH dapat dihitung menggunakan
Teorema Pythagoras
Back
Jadi, panjang diagonal bidang CH adalah 10
Next

22. b. Luas bidang CELH = luas persegipanjang CELH
=pxl
= CH x CL
= 10 x 8
= 80
jadi, luas bidang diagonal CELH adalah 64 cm
3. a. Luas permukaan prisma PQRSTU = (2 x luas PQR) +
(luas QRUT + luas RPSU)
=
=
Back
=
=
Next

23. b. Luas permukaan prisma PQRSTU tanpa tutup
= luas PQR + (luas PQTS + luas QRUT + luas RPSU)
= (PR x RQ)/2 + (PQ.QT + QR.RU + RP.PS)
= (8 x6)/2 + (10.7 + 6.7 + 8.7)
= 24 + 70 + 42 + 56
= 192
jadi, luas permukaan prisma segitiga tanpa tutup adalah 192 cm
4. a. Luas alas prisma segitiga ABC.DEF adalah luas ABC, sehingga
luas ABC = (AB x AC)/2
= (4 x3)/2
=6
jadi, luas alas prisma segitiga ABC.DEF adalah 6 cm
b. Volume prisma = luas alas x tinggi
238 cm = 34 x tinggi
tinggi = 238/34
tinggi = 7
Back
jadi, tinggi prisma tersebut adalah 7 cm
Finish

24. SOAL:
1. Hitunglah volume prisma segilima jika luas alasnya 50cm2
dan tinggi 15cm !
Penyelesaian :
Diketahui
: luas alas = 50cm2
Tinggi = 15 cm
Ditanya
: volume prisma ?
Jawab
:
Volume prisma = luas alas x tinggi
= 50cm2 x 15 cm
= 750cm3
Jadi, volume prisma adalah 750cm3
Back
Next

25. 2. sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi
masing – masing 9cm, 12cm, dan 15cm. Jika tinggi prisma
10cm, hitunglah luas permukaan prisma tersebut !
Penyelesaian :
Luas permukaan prisma = 2 x luas alas + ( keliling alas x tinggi)
= 2 ( ½ x 9 x 12) + (9 + 12 +15) x 10
= 2 x 54 + ( 36 x 10)
= 108 + 360
= 468 cm2
Jadi, luas permukaan prisma tersebut adalah 468 cm2
Back
Finish

26. Nama
Nim
Semester
: Enda Agwinata
: 2011121061
: 5B
Biodata: Enda adalah mahasiswa Universitas PGRI Palembang jurusan prodi
matematika semester 5, berasal dari OKU Timur sebagai anak rantau..
PENDIDIKAN MIPA
PENDIDIKAN MATEMATIKA
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS PGRI PALEMBANG
2013
Back
Next

27. Nama
Nim
Semester
: Eka Susanti
: 2011121074
: 5B
Biodata: Eka adalah mahasiswa Universitas PGRI Palembang jurusan prodi
matematika semester 5, berasal dari OKI sebagai anak rantau..
PENDIDIKAN MIPA
PENDIDIKAN MATEMATIKA
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS PGRI PALEMBANG
2013
Back
Next

28. Nama
Nim
Semester
: Ana Sari Yani
: 2011121067
: 5B
Biodata: Ana adalah mahasiswa Universitas PGRI Palembang jurusan prodi
matematika semester 5, berasal dari pusri palembang.
PENDIDIKAN MIPA
PENDIDIKAN MATEMATIKA
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS PGRI PALEMBANG
2013
Back
Next

29. Nama
Nim
Semester
: Agung Putra Miko
: 2011121066
: 5B
Biodata: agung adalah mahasiswa Universitas PGRI Palembang jurusan prodi
matematika semester 5, berasal dari OKU Selatan sebagai anak rantau..
PENDIDIKAN MIPA
PENDIDIKAN MATEMATIKA
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS PGRI PALEMBANG
2013
Back
Finish

30. Kesimpulan
Prisma adalah Memiliki bentuk alas dan atap yang sama
bentuk dan aturannya. Selain itu, semua sisi bagian samping
berbentuk persegi panjang.
 Sifat – sifat Prisma:
a) Prisma memiliki bentuk alas dan atap yang kongruen.
b) Setiap sisi bagian samping prisma berbentuk persegi
panjang.
c) Prisma memiliki rusuk tegak.
d) Setiap diagonal bidang pada sisi yang sama memiliki
ukuran yang sama.
Back
Next

31. Unsur yang harus dimiliki prisma:
 Sisi / bidang
 Rusuk
 Titik sudut
 Diagonal bidang
 Bidang diagonal
 Luas permukaan prisma = 2 x luas alas + luas bidang – bidang
tegak
 Luas permukaan prisma = 2 x luas alas + ( keliling alas x tinggi)
 Volume prisma = luas alas x tinggi
Back
Next

32. SELESAI