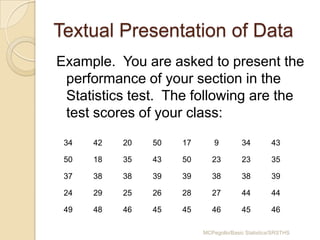
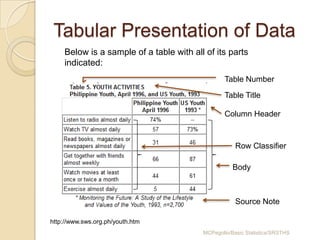
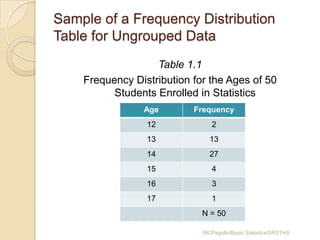
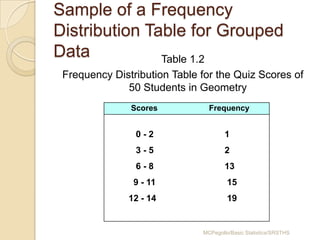
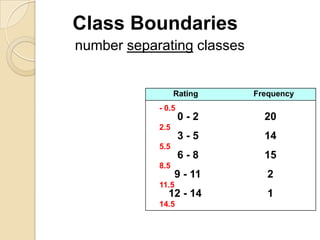
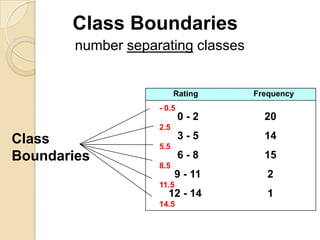
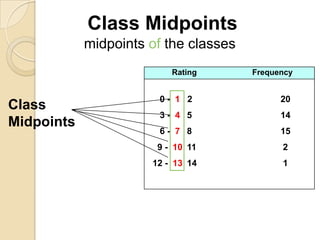
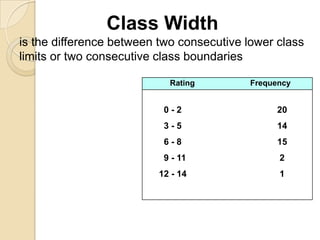
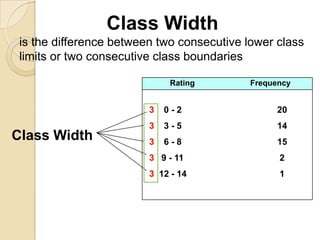
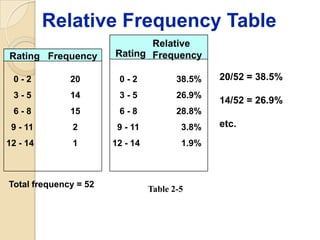
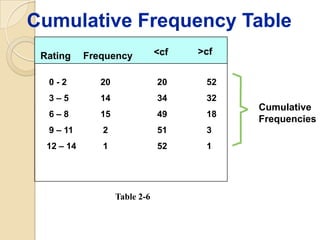
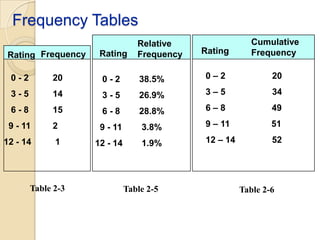
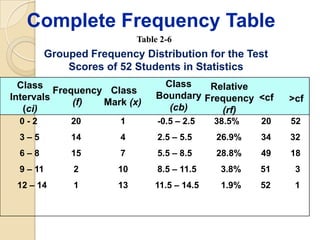
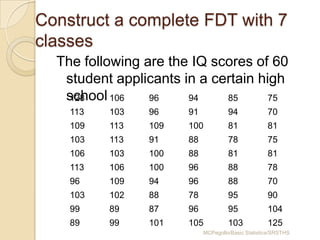
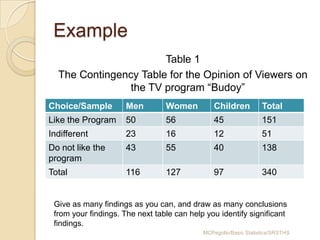
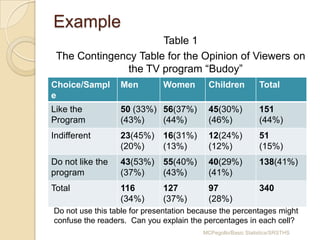
This document provides an overview of different methods for presenting data, including textual, tabular, and graphical methods. It discusses topics such as ungrouped versus grouped data, frequency distribution tables, stem-and-leaf plots, relative frequency tables, cumulative frequency tables, and contingency tables. Examples are provided to illustrate key concepts and techniques for organizing data using these various presentation methods. The objectives are to be able to prepare different types of tables and graphs, as well as read and interpret the information conveyed by these data visualization tools.

1. Presentation of Data
Module 6
Basic Statistics
SRSTHS
Ms. Pegollo

2. Presentation of Data
Objectives: At the end of the lesson,
the students should be able to:
1. Prepare a stem-and-leaf plot
2. Describe data in textual form
3. Construct frequency distribution table
4. Create graphs
5. Read and interpret graphs and tables
MCPegollo/Basic Statistics/SRSTHS

3. Ungrouped vs. Grouped Data
Data can be classified as grouped or
ungrouped.
Ungrouped data are data that are not
organized, or if arranged, could only be
from highest to lowest or lowest to
highest.
Grouped data are data that are
organized and arranged into different
classes or categories.
MCPegollo/Basic Statistics/SRSTHS

4. Presentation of Data
Textual
Method
Tabular
Method
Graphical
Method
• Rearrangem
ent from
lowest to
highest
• Stem-andleaf plot
• Frequency
distribution
table (FDT)
• Relative
FDT
• Cumulative
FDT
• Contingency
Table
• Bar Chart
• Histogram
• Frequency
Polygon
• Pie Chart
• Less than,
greater than
Ogive
MCPegollo/Basic Statistics/SRSTHS

5. Textual Presentation of Data
Data can be presented using
paragraphs or sentences. It involves
enumerating important characteristics,
emphasizing significant figures and
identifying important features of data.
MCPegollo/Basic Statistics/SRSTHS

6. Textual Presentation of Data
Example. You are asked to present the
performance of your section in the
Statistics test. The following are the
test scores of your class:
34
42
20
50
17
9
34
43
50
18
35
43
50
23
23
35
37
38
38
39
39
38
38
39
24
29
25
26
28
27
44
44
49
48
46
45
45
46
45
46
MCPegollo/Basic Statistics/SRSTHS

7. Solution
First, arrange the data in order for you to
identify the important characteristics. This
can be done in two ways: rearranging from
lowest to highest or using the stem-and-leaf
plot.
Below is the rearrangement of data from lowest
to highest:
9
23
28
35
38
43
45
48
17
24
29
37
39
43
45
49
18
25
34
38
39
44
46
50
20
26
34
38
39
44
46
50
23
27
35
38
42
45
46
50
MCPegollo/Basic Statistics/SRSTHS

8. With the rearranged data, pertinent data
worth mentioning can be easily
recognized. The following is one way
of presenting data in textual form.
In the Statistics class of 40
students, 3 obtained the perfect score
of 50. Sixteen students got a score of
40 and above, while only 3 got 19 and
below. Generally, the students
performed well in the test with 23 or
70% getting a passing score of 38 and
MCPegollo/Basic Statistics/SRSTHS

9. Another way of rearranging data is by
making use of the stem-and-leaf plot.
What is a stem-and-leaf plot?
Stem-and-leaf Plot is a table which
sorts data according to a certain pattern. It
involves separating a number into two parts.
In a two-digit number, the stem consists of
the first digit, and the leaf consists of the
second digit. While in a three-digit number,
the stem consists of the first two digits, and
the leaf consists of the last digit. In a onedigit number, the stem is zero.
MCPegollo/Basic Statistics/SRSTHS

10. Below is the stem-and-leaf plot of the
ungrouped data given in the example.
Stem
Leaves
0
9
1
7,8
2
0,3,3,4,5,6,7,8,9
3
4,4,5,5,7,8,8,8,8,9,9,9
4
2,3,3,4,4,5,5,5,6,6,6,8,9
5
0,0,0
Utilizing the stem-and-leaf plot, we can readily see the
order of the data. Thus, we can say that the top ten
got scores 50, 50, 50, 49, 48, 46, 46, 46,45, and 45
and the ten lowest scores are 9, 17, 18, 20,
MCPegollo/Basic Statistics/SRSTHS
23,23,24,25,26, and 27.

11. Exercise:
Prepare a stem-and-leaf plot and
present in textual form.
Stem
The ages Leaf teachers in a public
of 40
school
23
2 3,6,7,8,8,9
27
28
36
32
42 0,1,2,4,4,5,5,5,6,6,6,6,8,8,8,8,9,9
3 44
54
56
48
55
48
30
31
35
36
47
48
4 0,0,0,2,3,4,4,5,5,7,8,8,8
26
28
29
45
34
5 4,5,6
38
39
38
36
35
34
36
35
38
39
40
43
38
45
44
40
40
MCPegollo/Basic Statistics/SRSTHS

12. Tabular Presentation of Data
Below is a sample of a table with all of its parts
indicated:
Table Number
Table Title
Column Header
Row Classifier
Body
Source Note
http://www.sws.org.ph/youth.htm
MCPegollo/Basic Statistics/SRSTHS

13. Frequency Distribution Table
A frequency distribution table is a table
which shows the data arranged into
different classes(or categories) and
the number of cases(or frequencies)
which fall into each class.
The following is an illustration of a
frequency distribution table for
ungrouped data:
MCPegollo/Basic Statistics/SRSTHS

14. Sample of a Frequency Distribution
Table for Ungrouped Data
Table 1.1
Frequency Distribution for the Ages of 50
Students Enrolled in Statistics
Age
Frequency
12
2
13
13
14
27
15
4
16
3
17
1
N = 50
MCPegollo/Basic Statistics/SRSTHS

15. Sample of a Frequency
Distribution Table for Grouped
Data
Table 1.2
Frequency Distribution Table for the Quiz Scores of
50 Students in Geometry
Scores
Frequency
0-2
1
3-5
2
6-8
13
9 - 11
15
12 - 14
19
MCPegollo/Basic Statistics/SRSTHS

16. Lower Class Limits
are the smallest numbers that can actually belong
to different classes
Rating
Frequency
0-2
1
3-5
2
6-8
13
9 - 11
15
12 - 14
19

17. Lower Class Limits
are the smallest numbers that can
actually belong to different classes
Rating
0-2
Lower Class
Limits
Frequency
1
3-5
2
6-8
13
9 - 11
15
12 - 14
19

18. Upper Class Limits
are the largest numbers that can actually
belong to different classes
Rating
Frequency
0-2
1
3-5
2
6-8
13
9 - 11
15
12 - 14
19

19. Upper Class Limits
are the largest numbers that can actually
belong to different classes
Rating
Upper Class
Limits
Frequency
0-2
1
3-5
2
6-8
13
9 - 11
15
12 - 14
19

20. Class Boundaries
are the numbers used to separate classes,
but without the gaps created by class limits

21. Class Boundaries
number separating classes
Rating
- 0.5
0-2
20
3-5
14
6-8
15
9 - 11
2
2.5
5.5
8.5
Frequency
11.5
12 - 14
14.5
1

22. Class Boundaries
number separating classes
Rating
- 0.5
0-2
20
3-5
14
6-8
15
9 - 11
2
2.5
Class
Boundaries
5.5
8.5
Frequency
11.5
12 - 14
14.5
1

23. Class Midpoints
The Class Mark or Class Midpoint is the
respective average of each class limits

24. Class Midpoints
midpoints of the classes
Rating
Class
Midpoints
Frequency
0- 1 2
20
3- 4 5
14
6- 7 8
15
9 - 10 11
2
12 - 13 14
1

25. Class Width
is the difference between two consecutive lower class
limits or two consecutive class boundaries
Rating
Frequency
0-2
20
3-5
14
6-8
15
9 - 11
2
12 - 14
1

26. Class Width
is the difference between two consecutive lower class
limits or two consecutive class boundaries
Rating
Frequency
3
Class Width
0-2
20
3
3-5
14
3
6-8
15
3 9 - 11
2
3 12 - 14
1

27. Guidelines For Frequency Tables
1. Be sure that the classes are mutually exclusive.
2. Include all classes, even if the frequency is zero.
3. Try to use the same width for all classes.
4. Select convenient numbers for class limits.
5. Use between 5 and 20 classes.
6. The sum of the class frequencies must equal the
number of original data values.

28. Constructing A Frequency Table
1.
Decide on the number of classes .
2. Determine the class width by dividing the range by the number of
classes
(range = highest score - lowest score) and round
up.
range
class width

round up of
number of classes
3.
Select for the first lower limit either the lowest score or a
convenient value slightly less than the lowest score.
4.
Add the class width to the starting point to get the second lower
class limit, add the width to the second lower limit to get the
third, and so on.
5.
List the lower class limits in a vertical column and enter the
upper class limits.
6.
Represent each score by a tally mark in the appropriate class.
Total tally marks to find the total frequency for each class.

29. Homework
Gather data on the ages of your
classmates’ fathers, include your own.
Construct a frequency distribution table for
the data gathered using grouped and
ungrouped data.
What are the advantages and
disadvantages of using ungrouped
frequency distribution table?
What are the advantages and
disadvantages of using grouped
frequency distribution table?
MCPegollo/Basic Statistics/SRSTHS

30. Relative Frequency Table
relative frequency =
class frequency
sum of all frequencies

31. Relative Frequency Table
Rating Frequency
Relative
Rating Frequency
0-2
20
0-2
38.5%
3-5
14
3-5
26.9%
6-8
15
6-8
28.8%
9 - 11
2
9 - 11
3.8%
12 - 14
1
12 - 14
1.9%
20/52 = 38.5%
Total frequency = 52
Table 2-5
14/52 = 26.9%
etc.

32. Cumulative Frequency Table
>cf
Rating
Frequency
<cf
0-2
20
20
52
3–5
14
34
32
6–8
15
49
18
9 – 11
2
51
3
12 – 14
1
52
1
Table 2-6
Cumulative
Frequencies

33. Frequency Tables
Rating Frequency
Rating
Relative
Frequency
Rating
Cumulative
Frequency
0-2
20
0-2
38.5%
0–2
20
3-5
14
3-5
26.9%
3–5
34
6-8
15
6-8
28.8%
6–8
49
9 - 11
2
9 - 11
3.8%
9 – 11
51
12 - 14
1
12 - 14
1.9%
12 – 14
52
Table 2-3
Table 2-5
Table 2-6

34. Complete FDT
A complete FDT has class mark or
midpoint (x), class boundaries (c.b),
relative frequency or percentage
frequency, and the less than
cumulative frequency (<cf) and the
greater than cumulative frequency
(>cf).
MCPegollo/Basic Statistics/SRSTHS

35. Complete Frequency Table
Table 2-6
Grouped Frequency Distribution for the Test
Scores of 52 Students in Statistics
Class
Frequency Class
Intervals
(f)
Mark (x)
(ci)
Class
Relative
Boundary Frequency <cf
(cb)
(rf)
>cf
0-2
20
1
-0.5 – 2.5
38.5%
20
52
3–5
14
4
2.5 – 5.5
26.9%
34
32
6–8
15
7
5.5 – 8.5
28.8%
49
18
9 – 11
2
10
8.5 – 11.5
3.8%
51
3
12 – 14
1
13
11.5 – 14.5
1.9%
52
1

36. Exercise:
For each of the following class intervals, give
the class width(i), class mark (x), and class
boundary (cb)
Class interval (ci) Class Width
Class Mark
Class
Boundary
a. 4 – 8
b. 35 – 44
c. 17 – 21
d. 53 – 57
e. 8 – 11
f. 108 – 119
g. 10 – 19
h. 2.5 – 2. 9
i. 1. 75 – 2. 25
MCPegollo/Basic Statistics/SRSTHS

37. Construct a complete FDT with 7
classes
The following are the IQ scores of 60
student applicants in a certain high
school 106
128
96
94
85
75
113
103
96
91
94
70
109
113
109
100
81
81
103
113
91
88
78
75
106
103
100
88
81
81
113
106
100
96
88
78
96
109
94
96
88
70
103
102
88
78
95
90
99
89
87
96
95
104
89
99
101
105
103
125
MCPegollo/Basic Statistics/SRSTHS

38. Contingency Table
This is a table which shows the data
enumerated by cell. One type of such
table is the “r by c” (r x c) where the
columns refer to “c” samples and the
rows refer to “r” choices or
alternatives.
MCPegollo/Basic Statistics/SRSTHS

39. Example
Table 1
The Contingency Table for the Opinion of Viewers on
the TV program “Budoy”
Choice/Sample
Men
Women
Children
Total
Like the Program
50
56
45
151
Indifferent
23
16
12
51
Do not like the
program
43
55
40
138
Total
116
127
97
340
Give as many findings as you can, and draw as many conclusions
from your findings. The next table can help you identify significant
findings.
MCPegollo/Basic Statistics/SRSTHS

40. Example
Table 1
The Contingency Table for the Opinion of Viewers on
the TV program “Budoy”
Choice/Sampl
e
Men
Women
Children
Total
Like the
Program
50 (33%) 56(37%)
(43%)
(44%)
45(30%)
(46%)
151
(44%)
Indifferent
23(45%)
(20%)
16(31%)
(13%)
12(24%)
(12%)
51
(15%)
Do not like the
program
43(53%)
(37%)
55(40%)
(43%)
40(29%)
(41%)
138(41%)
Total
116
(34%)
127
(37%)
97
(28%)
340
Do not use this table for presentation because the percentages might
confuse the readers. Can you explain the percentages in each cell?
MCPegollo/Basic Statistics/SRSTHS