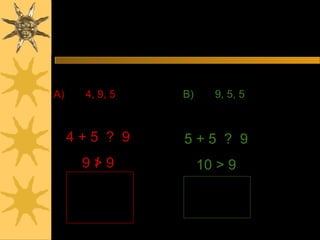
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. It can be written as inequalities comparing the different side lengths, such as AB + AC > BC. The converse is also true - the side opposite the largest angle will be the longest side. Examples demonstrate using the triangle inequality theorem to determine if a set of lengths could form a triangle or find the possible range of values for the third side of a triangle given two side lengths.

1. Triangle Inequality Theorem
The sum of the lengths of any two
sides of a triangle is greater than the
length of the third side

2. Inequalities in One Triangle
They have to be able to reach!!
3
2
4
3
6
3
3
6
6
Note that there is only one
situation that you can have a
triangle; when the sum of two
sides of the triangle are greater
than the third.

3. Triangle Inequality Theorem
A
AB + AC > BC
AB + BC > AC
AC + BC > AB
B
C

4. Triangle Inequality Theorem
Biggest Side Opposite Biggest Angle
A
Medium Side Opposite
Medium Angle
Smallest Side Opposite
Smallest Angle
3
5
B
C
m<B is greater than m<C

5. Triangle Inequality Theorem
Converse is true also
A
Biggest Angle Opposite
_____________
Medium Angle Opposite
______________
Smallest Angle Opposite
_______________
65
30
C
Angle A > Angle B > Angle C
So CB >AC > AB
B

6. Example: List the measures of the sides of the
triangle, in order of least to greatest.
B
<A = 2x + 1
<B = 4x
<C = 4x -11
Solving for x:
A
C
2x +1 + 4x + 4x - 11 =180
Note: Picture is not to scale
Plugging back into our
Angles:
<A = 39o; <B = 76; <C = 65
10x - 10 = 180
10x = 190
X = 19
Therefore, BC < AB < AC

7. Using the Exterior Angle
Inequality
Example: Solve the inequality if
AB + AC > BC
C
(x+3) + (x+ 2) > 3x - 2
x+3
2x + 5 > 3x - 2
x<7
3x - 2
A
x+2
B

8. Example: Determine if the following
lengths are legs of triangles
A)
4, 9, 5
B)
9, 5, 5
We choose the smallest two of the three sides and add
them together. Comparing the sum to the third side:
4+5 ? 9
5+5 ? 9
9>9
10 > 9
Since the sum is
not greater than
the third side,
this is not a
triangle
Since the sum is
greater than the
third side, this is
a triangle

9. Example: a triangle has side lengths of 6 and
12; what are the possible lengths of the third
side?
B
12
6
A
C
X=?
12 + 6 = 18
12 – 6 = 6
Therefore:
6 < X < 18

10. Example: a triangle has side lengths of 6 and
12; what are the possible lengths of the third
side?
B
12
6
A
C
X=?
12 + 6 = 18
12 – 6 = 6
Therefore:
6 < X < 18