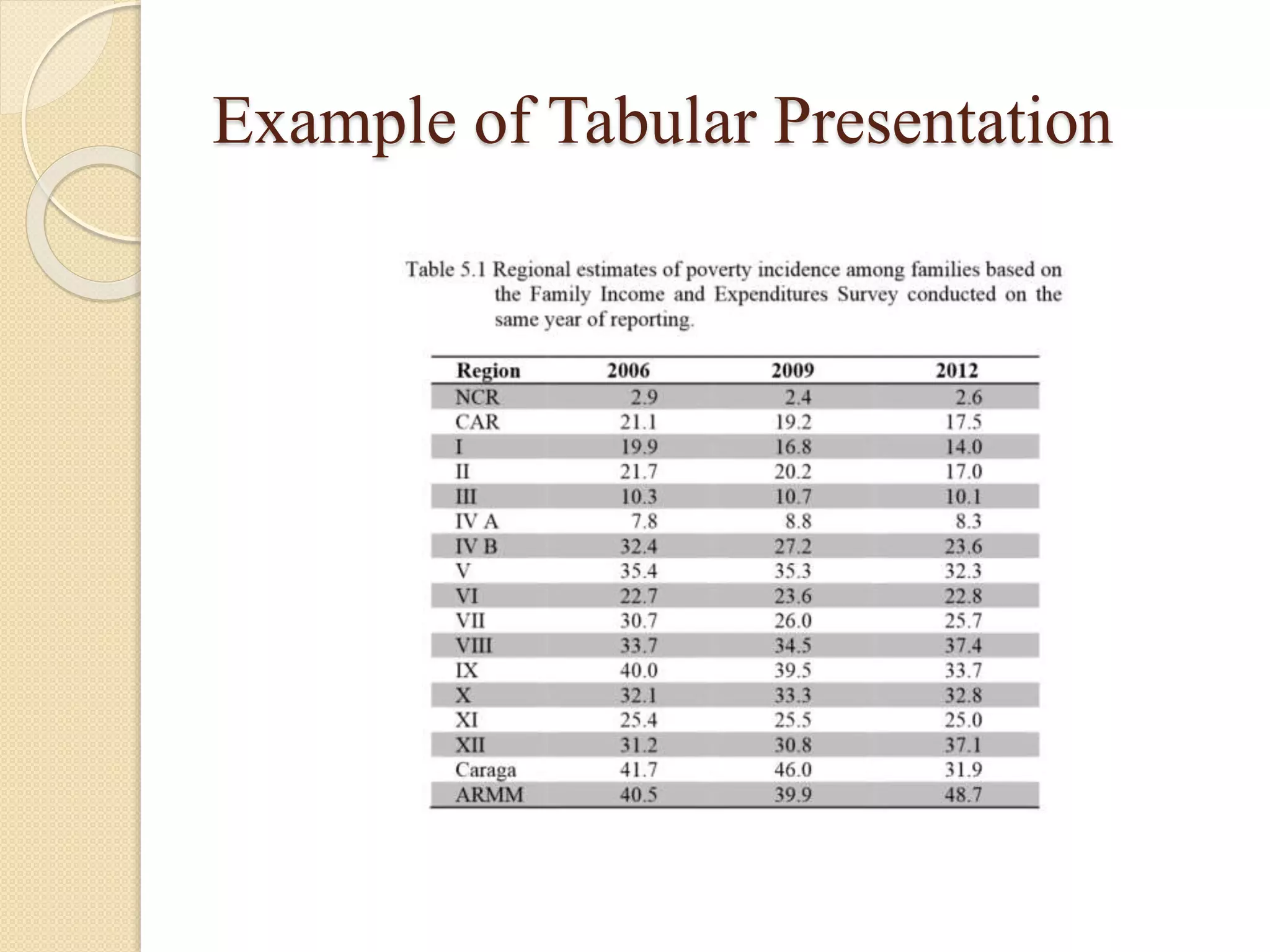
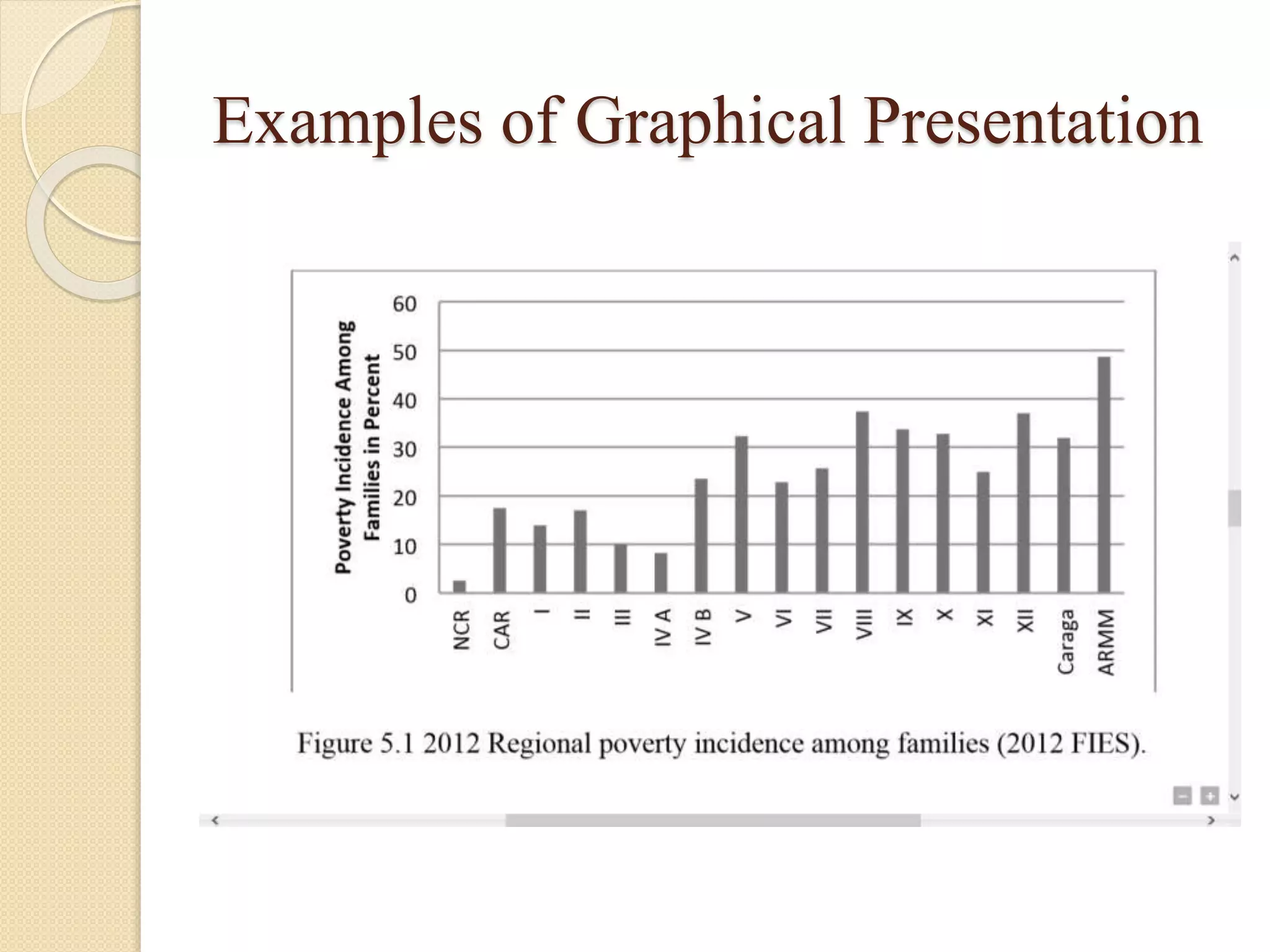
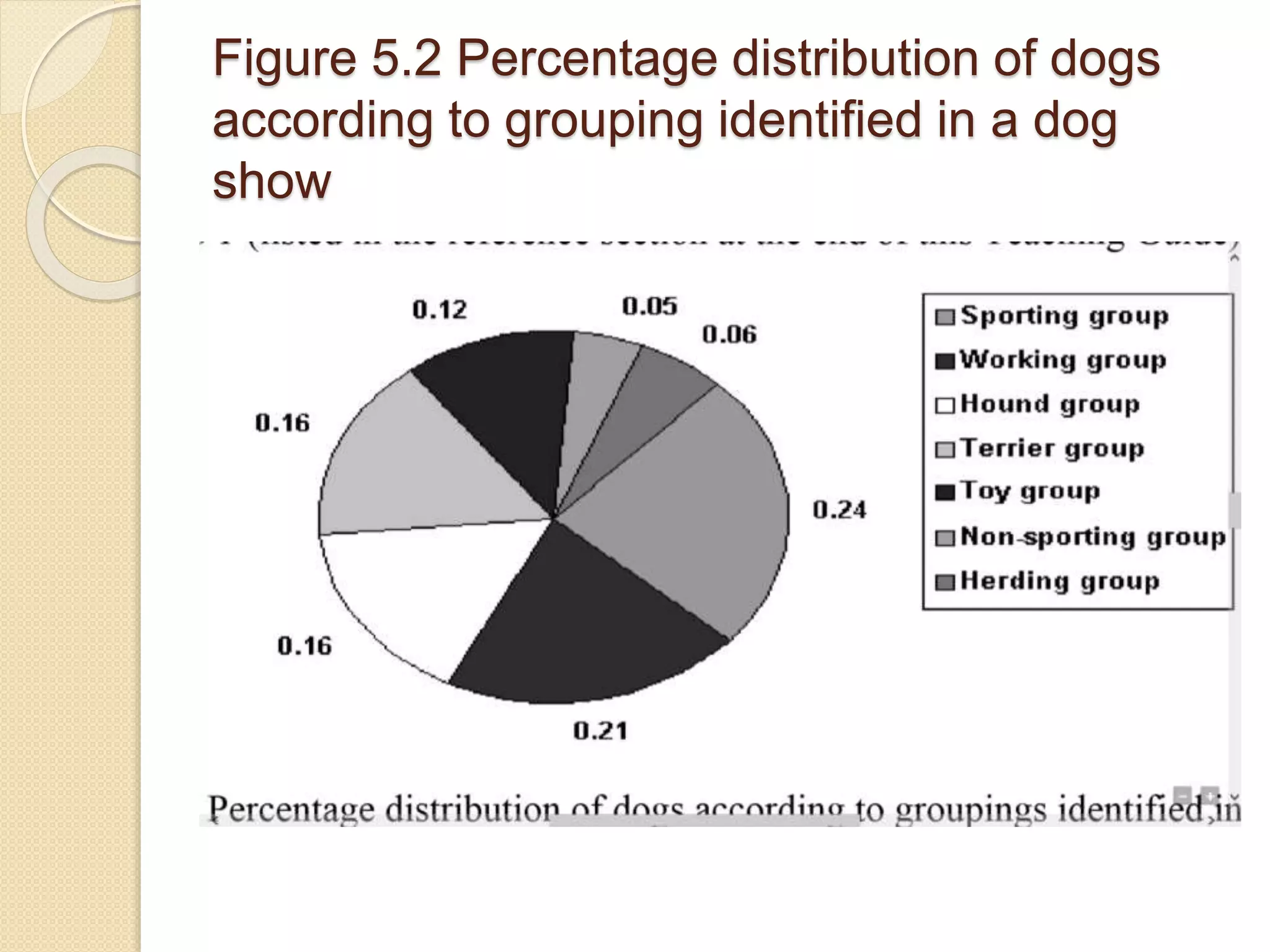
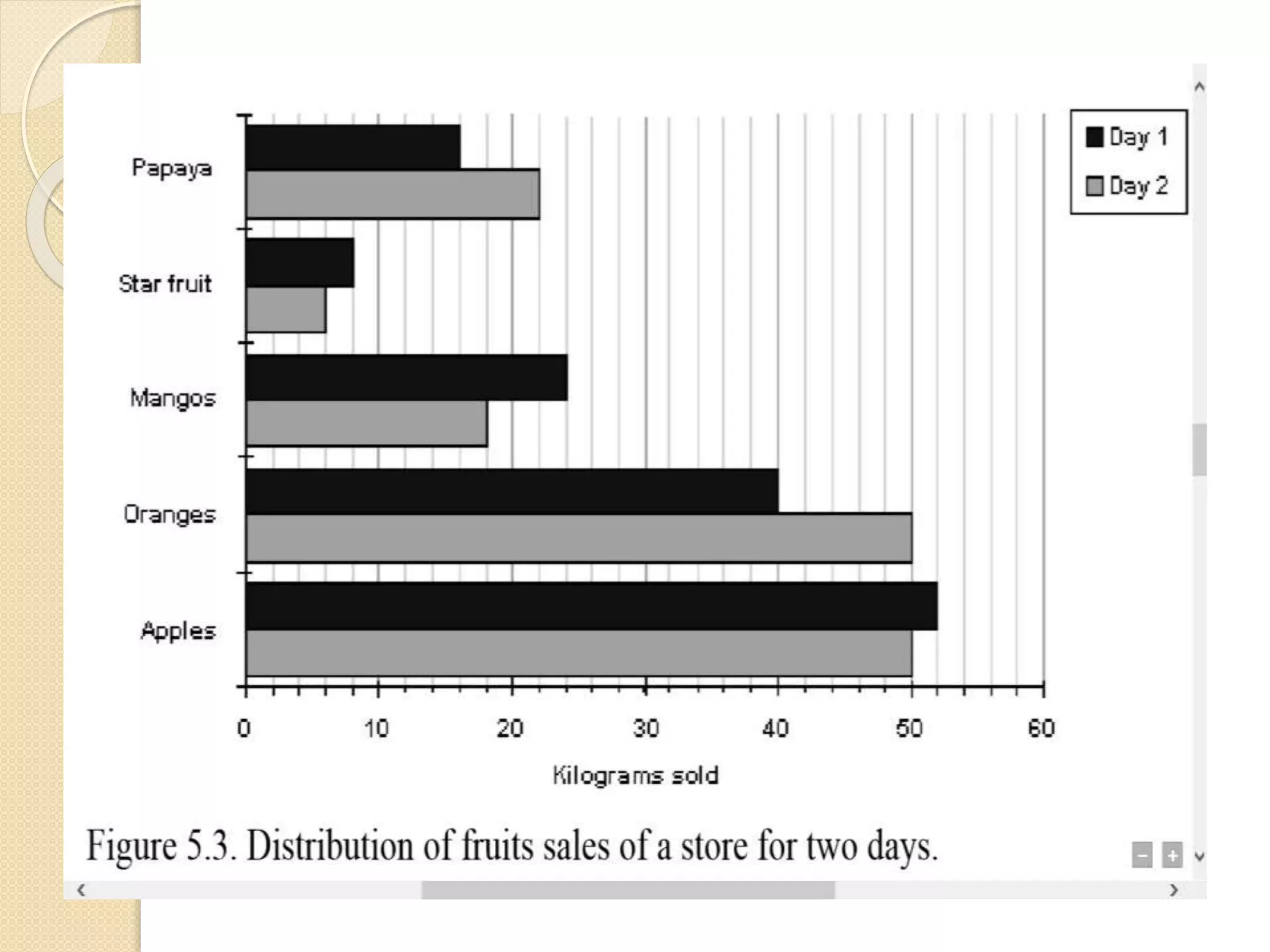
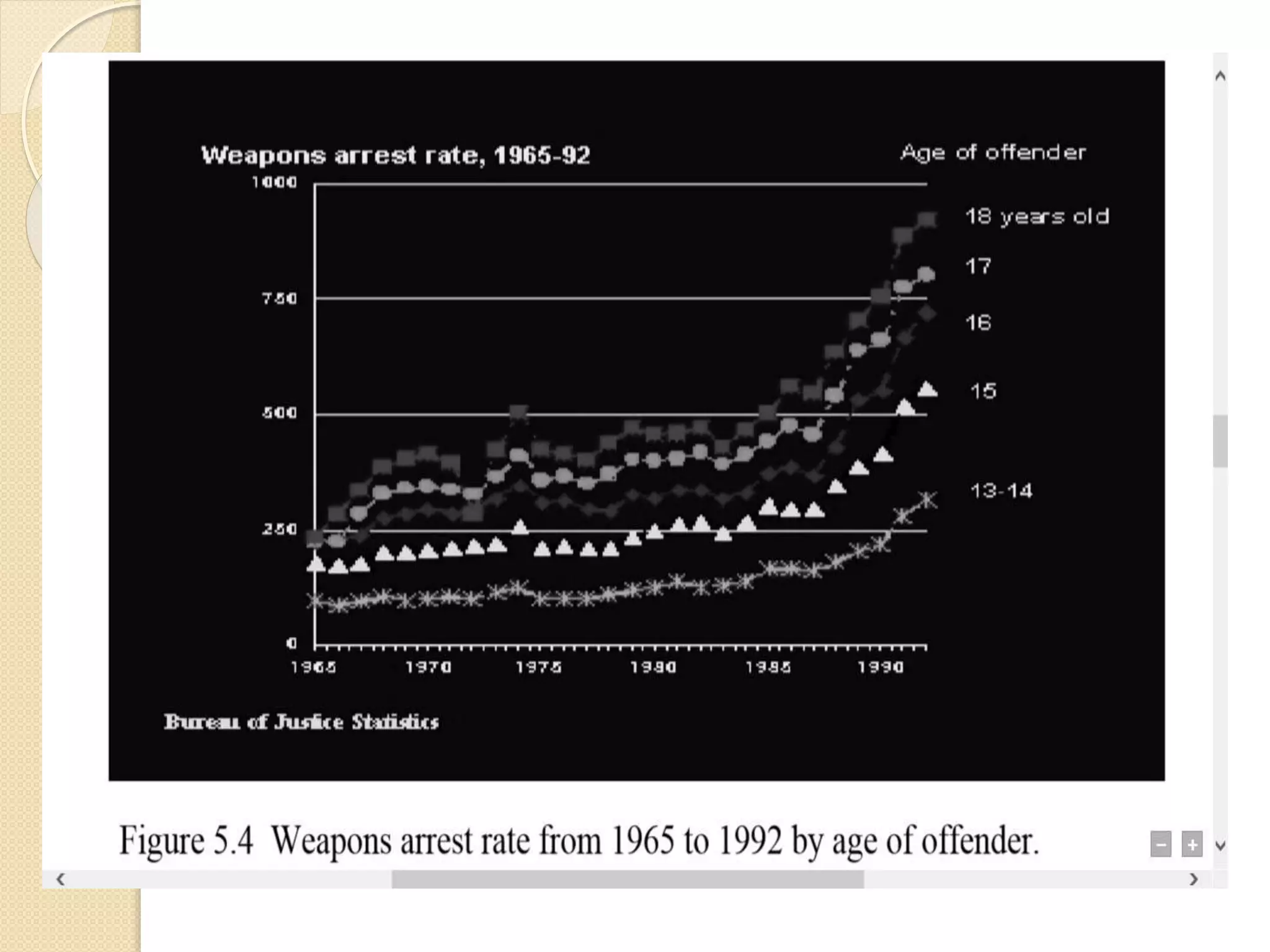
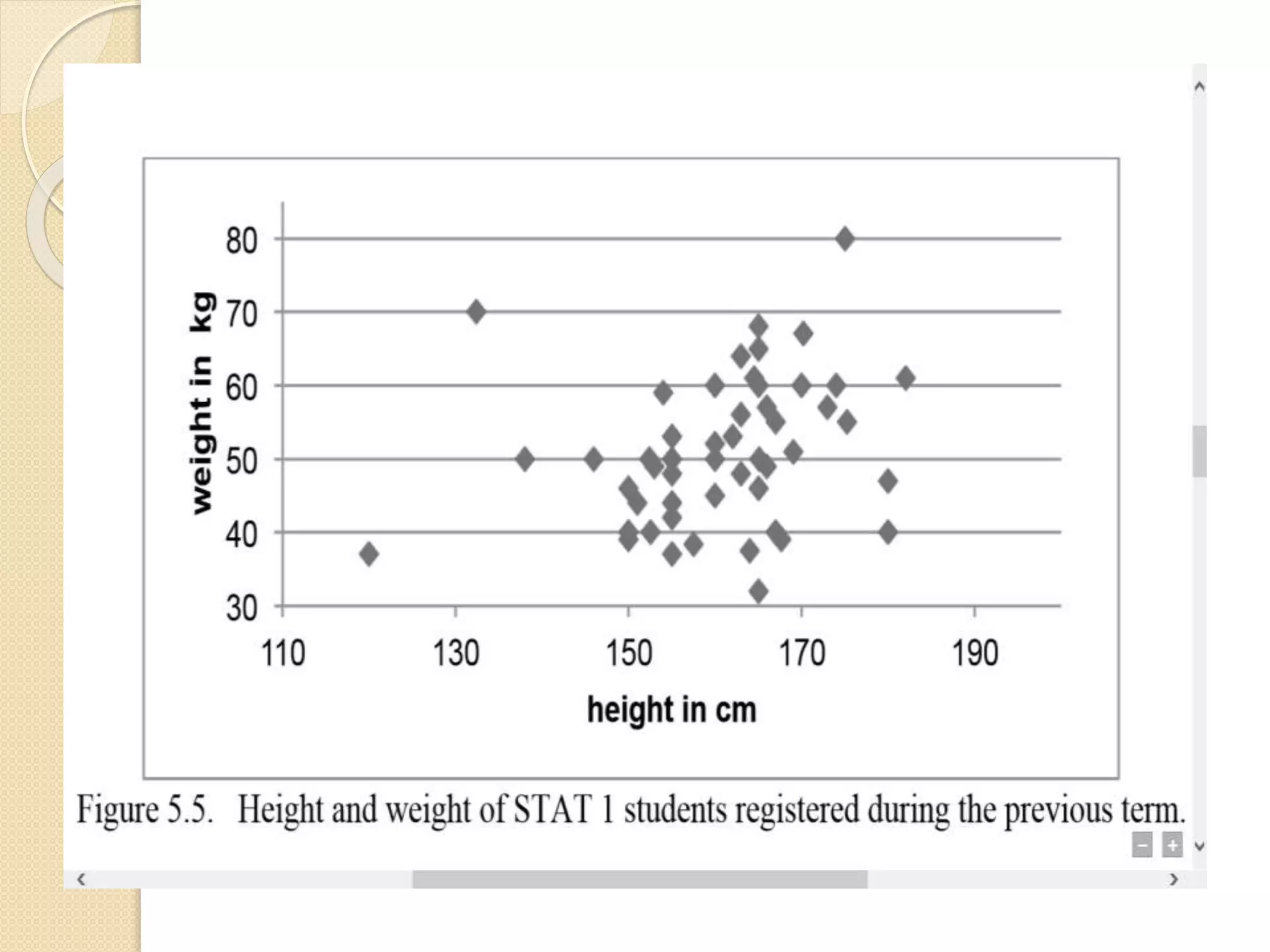
The document discusses different methods for presenting data, including textual, tabular, and graphical presentations. It provides examples and guidelines for each method, such as describing highlights in a paragraph, organizing values into a table with rows and columns, and using graphs like pie charts to visualize relationships. Frequency distribution tables and histograms are also covered as specialized forms of tabular and graphical presentation used to depict the distribution of quantitative data.

1. DATA
PRESENTATION

2. Learning Outcomes: At the
end of the lesson, the learner is
able to identify and use the
appropriate method of
presenting information from a
data set effectively.

3. A. Review the previous lessons.
 Levels of measurement
 Nominal Level
 Ordinal Level
 Interval Level
 Ratio Level
 Methods Of Data Collection
 Primary Data (objective and subjective)
 Secondary Data(use of existing records)

4. A. Methods of Data Presentation
Three methods of present data
1. Textual or Narrative
Presentation
2. Tabular Presentation
3. Graphical Presentation

5. 1. Textual or paragraph or narrative
presentation
Describes the data by
enumerating some of the
highlights of the data set like
giving the highest, lowest or the
average values.
In case there are only few
observation, say less than ten
observations, the values could be
enumerated if there is a need to do
so.

6. Example of textual Presentation
The country’s poverty incidence among
families as reported by the Philippine
Statistics Authority (PSA), the agency
mandated to release official poverty
statistics, decreases from 21% in 2006
down to 19.7% in 2012. For 2012, the
regional estimates released by PSA
indicate that the Autonomous Region of
Muslim Mindanao (ARMM) is the poorest
region with poverty incidence among
families estimated at 48.7%. The region
with the smallest estimated poverty
incidence among families at 2.6% is the
National Capital Region (NCR).

7. 2. Tabular Presentation
Applicable for large data sets.
Trend could easily be seen in this
kind presentation. However , there
is a loss information when using
such kind of presentation. The
frequency distribution table is
the usual tabular form of
presenting the distribution of the
data.

8. The following are the common
parts of a statistical table:
a) Table Title- includes the number
and a short description of what is
found inside the table.
b) Column Header- provides the label
of what is being presented in a
column.
c) Row Header –provides the label of
what is being presented in a row,
d) Body-are the information in the cell
intersecting the row and the
column.

9. Example of Tabular Presentation

10. 3. Graphical Presentation
Is a visual presentation of the
data.
Graphs are commonly used in oral
presentation.
There are several forms of graph to
use like the pie chart, pictograph,
bar graph, line graph, histogram
and box-plot.

11. Examples of Graphical Presentation

12. Figure 5.2 Percentage distribution of dogs
according to grouping identified in a dog
show

16. B. The Frequency Distribution
Table and Histogram
A special type of tabular and graphical
presentation is the frequency distribution
table(FDT) and its corresponding
histogram.
Specifically, these are used to depict the
distribution of the data. Most of the time,
these are used in technical reports.
Is a presentation containing non-
overlapping categories or classes of a
variable and the frequencies or counts of
the observations falling into the
categories or classes.

17. Two types of FDT according to
the type of data being organized:
i. Qualitative FDT-the non-overlapping
categories of the variable are
identified, and frequencies, as well as
the percentages of observations
falling into the categories, are
computed.
ii. Quantitative FDT-there are also two
types: ungrouped FDT and grouped
FDT.

18. Ungrouped FDT- is constructed when
there are only a few observations or if
the data set contains only few possible
values.
 Grouped FDT-is constructed when
there is a large number of observations
and when the data set involves many
possible values.

19. Steps in the construction of a
grouped FDT
1. Identify the largest data value or the maximum
(MAX) and smallest data value or the minimum
(MIN) from the data set and compute the range,
R. The range is the difference between the
largest and smallest value, i.e. R = MAX – MIN.
2. Determine the number of classes, k usingkN = ,
where N is the total number of observations in
the data set. Round-off k to the nearest whole
number. It should be noted that the computed k
might not be equal to the actual number of
classes constructed in an FDT.
3. Calculate the class size, c, using c = R/k. Round
off c to the nearest value with precision the same
as that with the raw data.

20. 4. Construct the classes or the class intervals.
A class interval is defined by a lower limit (LL)
and an upper limit (UL). The LL of the lowest
class is usually the MIN of the data set. The
LL’s of the succeeding classes are then
obtained by adding c to the LL of the
preceding classes. The UL of the lowest class
is obtained by subtracting one unit of
measure (1/10^x), where x is the maximum
number of decimal places observed from the
raw data) from the LL of the next class. The
UL’s of the succeeding classes are then
obtained by adding c to the UL of the
preceding classes. The lowest class should
contain the MIN, while the highest class
should contain the MAX.
5. Tally the data into the classes constructed in
Step 4 to obtain the frequency of each class.
Each observation must fall in one and only

21. 6. Add (if needed) the following distributional
characteristics:
a. True Class Boundaries (TCB). The TCBs reflect
the continuous property of a continuous data. It is
defined by a lower TCB (LTCB) and an upper
TCB (UTCB). These are obtained by taking the
midpoints of the gaps between classes or by
using the following formulas: LTCB = LL –
0.05(one unit of measure) and UTCB = UL +
0.05(one unit of measure).
b. Class Mark (CM). The CM is the midpoint of a
class and is obtained by taking the average of
the lower and upper TCB’s, i.e. CM = (LTCB +
UTCB)/2.
c. Relative Frequency (RF). The RF refers to the
frequency of the class as a fraction of the total
frequency, i.e. RF = frequency/N. RF can be
computed for both qualitative and quantitative
data. RF can also be expressed in percent.

22. d. Cumulative Frequency (CF). The CF
refers to the total number of observations
greater than or equal to the LL of the
class (>CF) or the total number of
observations less than or equal to the UL
of the class (<CF).
e. Relative Cumulative Frequency (RCF).
RCF refers to the fraction of the total
number of observations greater than or
equal to the LL of the class (>RCF) or
the fraction of the total number of
observations less than or equal to the UL
of the class (<RCF). Both the <RCF and
>RCF can also be expressed in percent.

23. Example of FDT and
Histogram
Using the Data Gathered from your
class. Make an FDT and Histogram.

24. Answer:
1.Choose a QUANTITATIVE variable
from the given data set. Compute R, k,
and c. Also construct a histogram for
the data. Use appropriate labels and
titles for the table and graph. Describe
the characteristics of the units in the
data set using a brief narrative report.

26. Textual Presentation:
________________________
________________________
____________________________
Which of the three methods of data
presentation do you think is most
appropriate to use for the variable ?
Justify your answer

27. 2.Choose a QUALITATIVE variable from
the data. Construct an appropriate
graph. Use label and a title for the
graph.
Give a brief report describing the
variable:
________________________________
______________________________
______________________________.