The document discusses various forms of quantum cryptography, including position-based quantum cryptography, device-independent quantum cryptography, and post-quantum cryptography. It emphasizes the theoretical advancements and practical implications of these cryptographic methods, as well as the challenges posed by quantum computing to existing cryptographic protocols. The research highlights the secure communication potential of quantum cryptography while addressing the evolving threat of quantum attacks on traditional algorithms.

1. Position-Based Quantum Cryptography
Device-Independent Quantum Cryptography
Post-Quantum Cryptography
Martins Jr. Divine Okoi

2. Content
 Background
 Position - Based Quantum Cryptography
 Device - Independent Quantum Cryptography
 Post - Quantum Cryptography
 Sources

3. Background
Quantum cryptography is the science of exploiting quantum mechanical properties to perform
cryptographic tasks. The best known example of quantum cryptography is quantum key distribution
which offers an information-theoretically secure solution to the key exchange problem.
Quantum cryptography makes use of the quantum-mechanical behaviour of nature for the design and
analysis of cryptographic schemes. Its aim is to design cryptographic schemes whose security is
guaranteed solely by the laws of nature. This is in sharp contrast to most standard cryptographic
schemes, which in principle, can be broken, i.e., when given sufficient computing power. From a
theoretical point of view, quantum cryptography offers a beautiful interplay between the mathematics
of adversarial behaviour and quantum information theory.

4. Position - Based Quantum Cryptography
(What is it?)
The goal of position-based cryptography is to use the geographical location of a player as its (only)
credential. For example, one wants to send a message to a player at a specified position with the
guarantee that it can only be read if the receiving party is located at that particular position. In the
basic task of position-verification, a player Alice wants to convince the (honest) verifiers that she is
located at a particular point. A more advanced task is secure position-based authentication where it is
guaranteed that a received message originated from a particular position and was not modified.

5. Position - Based Quantum Cryptography

6. Position - Based Quantum Cryptography
Position-based cryptography has a number of interesting
applications. For example, it enables secure communication
over an insecure channel without having any pre-shared
key, with the guarantee that only a party at a specific
location can learn the content of the conversation; think of
a military commander who wants to communicate with a
base which is surrounded by enemy territory, or a country
that wants to send instructions to an embassy in a foreign
country. Another application is authenticity verification,
where position-based cryptography enables users to verify
that a received message originates from a particular
geographical position and was not modified during the
transmission. Another is access control to resources

7. Position - Based Quantum Cryptography
In 2009, it was proven by collaborators from the University of California in Los Angeles (UCLA) that position-
based cryptography is impossible in the classical (non-quantum) world in the setting where colluding
opponents control the whole space which is not occupied by honest players. In their latest research article,
they investigated whether the impossibility of position-based cryptography can be overcome if they allow
the players to use quantum communication.
The outcome of their theoretical investigation demonstrates that the possibility of doing secure position-
based cryptography depends on the opponents' capability of sharing entangled quantum states. On the one
hand, they showed that if the opponents cannot share any entangled quantum state, then secure position-
based cryptography is possible. They presented a scheme which allows a player, Alice, to convince the other
participants in the protocol that she is at a particular geographical position. In contrast, colluding opponents
who are not at this position and do not share any entangled quantum state will be detected lying if they
claim to be there. They claim their scheme is very simple and can be implemented with today's QKD
hardware.

8. Position - Based Quantum Cryptography
On the other hand, they also showed that if the opponents are able to share a huge entangled
quantum state, then any positioning scheme can be broken and no position-based cryptography is
possible at all. In fact, their result shows how colluding opponents can use their entangled state to
instantaneously and non-locally perform the honest player's operations and are therefore able to make
it appear as if they were at the claimed position.
Their results raise various interesting research questions. For example, it is a formidable technical
challenge to store and handle large quantum states. Hence, is secure position-based cryptography
possible in the realistic setting where opponents can only handle a limited amount of entangled
quantum states? Their investigation has already sparked several follow-up works and first results
indicate that there are schemes which remain secure in this bounded-entanglement setting.

9. Position - Based Quantum Cryptography
 Basic Task
 One Dimension

10. Position - Based Quantum Cryptography
Classical Scheme:
Impossible

11. Position - Based Quantum Cryptography
Quantum Based
Position Verification

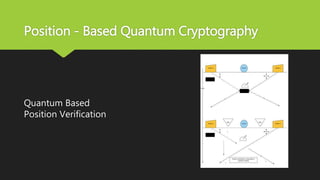
12. Position - Based Quantum Cryptography
(History)
 2003/2006 [Kent Munro Spiller, Hp Labs]: Quantum Tagging
 March 2010 [Malaney, arxiv, Australian Phiscisist]: Quantum Scheme for Position verification,
rigorous proof, but implicitly assuming no pre-shared entanglement
 2010 [Kent Munro Spiller arxiv]: Insecurity of Proposed scheme, new (secure) schemes?
 Sep. 2010 [bulo, arxiv]: extension of Kent et al’s attack, proposal of new (secure?) scheme
 Sep. 2010 [arxiv] impossibility of position-based quantum cryptography

13. Position - Based Quantum Cryptography
(Summary)
 Plain Model: Classically and Quantum impossible to use the prover’s location as the only credential
 Basic scheme for secure positioning if adversaries have no pre-shared entanglement
 Can be generalized to more dimensions

14. Position - Based Quantum Cryptography
(Further Study)
 Quantum Teleportation
 Instantaneous Non-Local Q Computation
 Impossibility of any Position-Based Q
Cryptography
 Quantum Teleportation Attack
 Works against multi-round schemes
 Unless entanglement isn’t shared

15. Device - Independent Quantum Cryptography
A quantum cryptographic protocol is device-independent if its security does not rely on trusting that
the quantum devices used are truthful. Thus the security analysis of such a protocol needs to consider
scenarios of imperfect or even malicious devices. Several important problems have been shown to
admit unconditional secure and device-independent protocols.

16. Device - Independent Quantum Cryptography
Quantum key distribution (QKD) is a provably secure way for two distant parties to establish a common
secret key, which then can be used in a classical cryptographic scheme. Using quantum entanglement,
one can reduce the necessary assumptions that the parties have to make about their devices, giving rise
to device-independent QKD (DIQKD). However, in all existing protocols to date the parties need to have
an initial (at least partially) random seed as a resource.
Using recent advances in the fields of randomness amplification and randomness expansion, it was
demonstrated that it is sufficient for the message the parties want to communicate to be (partially)
unknown to the adversaries – an assumption without which any type of cryptography would be
pointless to begin with. One party can use her secret message to locally generate a secret sequence of
bits, which can then be openly used by herself and the other party in a DIQKD protocol. Hence, work has
been done which reduces the requirements needed to perform secure DIQKD and establish safe
communication.

17. Post - Quantum Cryptography
Post-quantum cryptography refers to cryptographic algorithms (usually public-key algorithms) that are
thought to be secure against an attack by a quantum computer.
This is not true of the most popular public-key algorithms which can be efficiently broken by a sufficiently
large quantum computer. The problem with the currently popular algorithms is that their security relies
on one of three hard mathematical problems: the integer factorization problem, the discrete logarithm
problem or the elliptic curve discrete logarithm problem.
All of these problems can be easily solved on a sufficiently large quantum computer running Shor's
algorithm. Even though current, publicly known, experimental quantum computers are too small to
attack any real cryptographic algorithm, many cryptographers are designing new algorithms to prepare
for a time when quantum computing becomes a threat. This work has gained greater attention from
academics and industry through the PQCrypto conference series since 2006 and more recently by several
European Telecommunications Standards Institute (ETSI) Workshops on Quantum Safe Cryptography.

18. Post - Quantum Cryptography
In contrast to the threat quantum computing poses to current public key algorithms, most current
symmetric cryptographic algorithms (symmetric ciphers :algorithms are algorithms for cryptography that
use the same cryptographic keys for both encryption of plaintext and decryption of ciphertext. The keys
may be identical or there may be a simple transformation to go between the two keys. The keys, in
practice, represent a shared secret between two or more parties that can be used to maintain a private
information link) and hash functions :any function that can be used to map data of arbitrary size to data of
fixed size.

19. Post - Quantum Cryptography
The values returned by a hash function are called hash values, hash codes, hash sums, or simply hashes.
One use is a data structure called a hash table, widely used in computer software for rapid data lookup)
are considered to be relatively secure from attacks by quantum computers. While the
quantum Grover's algorithm (a quantum algorithm that finds with high probability the unique input to
a black box function that produces a particular output value, using just O(N) evaluations of the
function, where N is the size of the function's domain) does speed up attacks against symmetric
ciphers, doubling the key size can effectively block these attacks.

20. Post - Quantum Cryptography
Imagine that it’s fifteen years from now and someone announces the successful construction of a large
quantum computer. The New York Times runs a front page article reporting that all of the public-key
algorithms used to protect the Internet have been broken. Users panic. What exactly will happen to
cryptography? Perhaps, after seeing quantum computers destroy RSA and DSA and ECDSA, Internet
users will leap to the conclusion that cryptography is dead; that there is no hope of scrambling
information to make it incomprehensible to, and unforgeable by, attackers; that securely storing and
communicating information means using expensive physical shields to prevent attackers from seeing
the information—for example, hiding USB sticks inside a locked briefcase chained to a trusted courier’s
wrist. A closer look reveals, however, that there is no justification for the leap from “quantum
computers destroy RSA and DSA and ECDSA” to “quantum computers destroy cryptography.” There
are many important classes of cryptographic systems beyond RSA and DSA and ECDSA:

21. Post - Quantum Cryptography
(Algorithms Used and Their Security Downsides)
Algorithms Used
 Hash-Based
 Code Based
 Multivariable
 Lattice Based
 Supersingular Elliptic Curve Isogeny
 Symmetric Key Quantum Resistance

22. Post - Quantum Cryptography
(A hash-based public-key signature system)
This signature system requires a standard cryptographic hash function H that produces 2b bits of output.
For b = 128 one could choose H as the SHA256 hash function. Over the last few years many concerns
have been raised regarding the security of popular hash functions, and over the next few years NIST will
run a competition for a SHA-256 replacement, but all known attacks against SHA-256 are extremely
expensive. The signer’s public key in this system has 8b2 bits: e.g., 16 kilobytes for b = 128. The key
consists of 4b strings y1[0],y1[1],y2[0],y2[1],...,y2b[0],y2b[1], each string having 2b bits. A signature of a
message m has 2b(2b + 1)bits: e.g., 8 kilobytes for b = 128. The signature consists of 2b-bit strings
r,x1,...,x2b such that the bits (h1,...,h2b) of H(r,m) satisfy y1[h1]=H(x1), y2[h2]=H(x2), and so on through
y2b[h2b]=H(x2b).
How does the signer find x with H(x)=y? By generating a secret x and then computes y = H(x).
Specifically, the signer’s secret key has 8b2 bits, namely 4b independent uniform random strings
x1[0],x1[1],x2[0],x2[1],...,x2b[0],x2b[1], each string having 2b bits. The signer computes the public key
y1[0],y1[1],y2[0],y2[1],...,y2b[0],y2b[1] as H(x1[0]),H(x1[1]),H(x2[0]),H(x2[1]),...,H(x2b[0]),H(x2b[1]).

23. Post - Quantum Cryptography
(A hash-based public-key signature system)
To sign a message m, the signer generates a uniform random string r, computes the bits (h1,...,h2b) of H(r,m),
and reveals(r,x1[h1],...,x2b[h2b]) as a signature of m. The signer then discards the remaining x values and
refuses to sign any more messages. What I’ve described so far is the “Lamport–Diffie one-time signature
system.” What do we do if the signer wants to sign more than one message? An easy answer is “chaining.”
The signer includes, in the signed message, a newly generated public key that will be used to sign the next
message. The verifier checks the first signed message, including the new public key, and can then check the
signature of the next message; the signature of the nth message includes all n−1 previous signed messages.
More advanced systems, such as Merkle’s hash-tree signature system, scale logarithmically with the number
of messages signed. To me hash-based cryptography is a convincing argument for the existence of secure
post-quantum public-key signature systems. Grover’s algorithm is the fastest quantum algorithm to invert
generic functions, and is widely believed to be the fastest quantum algorithm to invert the vast majority of
specific efficiently computable functions (although obviously there are also many exceptions, i.e., functions
that are easier to invert).

24. Post - Quantum Cryptography
(A hash-based public-key signature system)
Hash-based cryptography can convert any hard-to-invert function into a secure public-key signature
system. See the “Hash-based digital signature schemes” chapter of this book for a much more detailed
discussion of hash-based cryptography. Note that most hash-based systems impose an extra
requirement of collision resistance upon the hash function, allowing simpler signatures without
randomization.

25. Post - Quantum Cryptography
(A code-based public-key encryption system)
Assume that b is a power of 2. Write n =4 blgb; d = ⌈lgn⌉; andt = ⌊0.5n/d⌋.For example, if b = 128,
thenn = 3584; d = 12; andt = 149. The receiver’s public key in this system is a dt×n matrix K with
coefficients in F2. Messages suitable for encryption are n-bit strings of “weight t,” i.e., n-bit strings
having exactly t bits set to 1. To encrypt a message m, the sender simply multiplies K by m, producing
a dt-bit ciphertext Km. The basic problem for the attacker is to “syndrome-decode K,” i.e., to undo the
multiplication by K, knowing that the input had weight t. It is easy, by linear algebra, to work
backwards from Km to some n-bit vector v such that Kv = Km; however, there are a huge number of
choices for v, and finding a weight-t choice seems to be extremely difficult. The best known attacks on
this problem take time exponential in b for most matrices K. How, then, can the receiver solve the same
problem? The answer is that the receiver generates the public key K with a secret structure, specifically
a “hidden Goppa code” structure, that allows the receiver to decode in a reasonable amount of time. It
is conceivable that the attacker can detect the “hidden Goppa code” structure in the public key, but no
such attack is known.

26. Post - Quantum Cryptography
(A code-based public-key encryption system)
Specifically, the receiver starts with distinct elements α1,α2,...,αn of the field F2d and a secret monic degree-t
irreducible polynomial g ∈ F2d[x]. The main work for the receiver is to syndrome-decode the dt×n matrix
where each element of F2d is viewed as a column of d elements of F2 in a standard basis of F2d. This matrix
H is a “parity-check matrix for an irreducible binary Goppa code,” and can be syndrome-decoded by
“Patterson’s algorithm” or by faster algorithms.
The receiver’s public key K is a scrambled version of H. Specifically, the receiver’s secret key also includes an
invertible dt×dt matrix S and an n× n permutation matrix P. The public key K is the product SHP. Given a
ciphertext Km = SHPm, the receiver multiplies by S−1 to obtain HPm, decodes H to obtain Pm, and
multiplies by P−1 to obtain m. What I’ve described here is a variant, due to Niederreiter (1986), of McEliece’s
original code-based public-key encryption system. Both systems are extremely efficient at key generation,
encryption, and decryption, but—as I mentioned earlier—have been held back by their long public keys. See
the “Code-based cryptography” and “Lattice-based cryptography” chapters of this book for much more
information about code-based cryptography and (similar but more complicated) lattice-based cryptography,
including several systems that use shorter public keys.

27. Post - Quantum Cryptography
(Challenges)
Some cryptographic systems, such as RSA with a four-thousand-bit key, are believed to resist attacks
by large classical computers but do not resist attacks by large quantum computers. Some alternatives,
such as McEliece encryption with a four-million-bit key, are believed to resist attacks by large classical
computers and attacks by large quantum computers. So why do we need to worry now about the
threat of quantum computers? Why not continue to focus on RSA and ECDSA? If someone announces
the successful construction of a large quantum computer fifteen years from now, why not simply switch
to McEliece etc. fifteen years from now? This section gives three answers—three important reasons that
parts of the cryptographic community are already starting to focus attention on postquantum
cryptography:

28. Post - Quantum Cryptography
(Challenges)
• We need time to improve the efficiency of post-quantum cryptography.
• We need time to build confidence in post-quantum cryptography.
• We need time to improve the usability of post-quantum cryptography. In short, we are not yet
prepared for the world to switch to post-quantum cryptography.
Maybe this preparation is unnecessary. Maybe we won’t actually need post-quantum cryptography.
Maybe nobody will ever announce the successful construction of a large quantum computer. However,
if we don’t do anything, and if it suddenly turns out years from now that users do need post-quantum
cryptography, years of critical research time will have been lost.

29. Post - Quantum Cryptography
(Challenges: Efficiency)
Elliptic-curve signature systems with O(b)-bit signatures and O(b)-bit keys appear to provide b bits of
security against classical computers. State-of-the art signing algorithms and verification algorithms
take time b2+o(1). Can post-quantum public-key signature systems achieve similar levels of
performance? My two examples of signature systems certainly don’t qualify: one example has
signatures of length b2+o(1), and the other example has keys of length b3+o(1). There are many other
proposals for post-quantum signature systems, but I have never seen a proposal combining O(b)-bit
signatures, O(b)bit keys, polynomial-time signing, and polynomial-time verification. Inefficient
cryptography is an option for some users but is not an option for a busy Internet server handling tens
of thousands of clients each second. If you make a secure web connection today to
https://www.google.com, Google redirects your browser to http://www.google.com, deliberately
turning off cryptographic protection. Google does have some cryptographically protected web pages
but apparently cannot afford to protect its most heavily used web pages. If Google already has trouble
with the slowness of today’s cryptographic

30. Post - Quantum Cryptography
(Challenges: Efficiency)
software, surely it will not have less trouble with the slowness of post-quantum cryptographic software.
Constraints on space and time have always posed critical research challenges to cryptographers and
will continue to pose critical research challenges to post-quantum cryptographers. On the bright side,
research in cryptography has produced many impressive speedups, and one can reasonably hope that
increased research efforts in post-quantum cryptography will continue to produce impressive
speedups.

31. Post - Quantum Cryptography
(Challenges: Confidence)
Merkle’s hash-tree public-key signature system and McEliece’s hidden-Goppacode public-key
encryption system were both proposed thirty years ago and remain essentially unscathed despite
extensive cryptanalytic efforts. Many other candidates for hash-based cryptography and code-based
cryptography are much newer; multivariate-quadratic cryptography and lattice based cryptography
provide an even wider variety of new candidates for postquantum cryptography. Some specific
proposals have been broken. Perhaps a new system will be broken as soon as a cryptanalyst takes the
time to look at the system. One could insist on using classic systems that have survived many years of
review. But often the user cannot afford the classic systems and is forced to consider newer, smaller,
faster systems that take advantage of more recent research into cryptographic efficiency. To build
confidence in these systems the community needs to make sure that cryptanalysts have taken time to
search for attacks on the systems. Those cryptanalysts, in turn, need to gain familiarity with post-
quantum cryptography and experience with post-quantum cryptanalysis.

32. Post - Quantum Cryptography
(Challenges: Usability)
The RSA public-key cryptosystem started as nothing more than a trapdoor one-way function, “cube
modulo n.” (Tangential historical note: The original paper by Rivest, Shamir, and Adleman actually used
large random exponents. Rabin pointed out that small exponents such as 3 are hundreds of times
faster.) Unfortunately, one cannot simply use a trapdoor one-way function as if it were a secure
encryption function. Modern RSA encryption does not simply cube a message modulo n; it has to first
randomize and pad the message. Furthermore, to handle long messages, it encrypts a short random
string instead of the message, and uses that random string as a key for a symmetric cipher to encrypt
and authenticate the original message. This infrastructure around RSA took many years to develop,
with many disasters along the way, such as the “PKCS#1 v1.5” padding standard broken by
Bleichenbacher in 1998

33. Post - Quantum Cryptography
(Challenges: Usability)
Furthermore, even if a secure encryption function has been defined and standardized, it needs software
implementations—and perhaps also hardware implementations—suitable for integration into a wide
variety of applications. Implementors need to be careful not only to achieve correctness and speed but
also to avoid timing leaks and other side-channel leaks. A few years ago several implementations of
RSA and AES were broken by cache-timing attacks; Intel has, as a partial solution, added AES
instructions to its future CPUs. Post-quantum cryptography, like the rest of cryptography, needs
complete hybrid systems and detailed standards and high-speed leak-resistant implementations.

34. Sources
 Alves, Carolina Moura and Kent Adrian. "Quantum Cryptography." National University of Singapore.
http://www.quantumlah.org/?q=tutorial/quantumcrypto
 Azzole, Pete. "Ultra: The Silver Bullet." Crypotolog. November 1996.
http://www.cl.cam.ac.uk/research/security/Historical/azzole1.html
 Brumfiel, Geoffrey. "Quantum Cryptography is Hacked." Nature. April 27, 2007.
http://www.nature.com/news/2007/070423/full/news070423-10.html

35. Sources
 Edgar A Aguilar, Ravishankar Ramanathan, Johannes Kofler4, and Marcin Pawłowski, Completely Device
Independent Quantum Key Distribution. arXiv:1507.05752v1 [quant-ph] 21 Jul 2015
 Messmer, Ellen. "Quantum Cryptography to Secure Ballots in Swiss Election." Network World. October 11,
2007. http://www.networkworld.com/news/2007/101007-quantum-cryptography-secure-
ballots.html?t51hb
 Stix, Gary. "Best-Kept Secrets: Quantum cryptography has marched from theory to laboratory to real
products." Scientific American. January 2005.
http://www.sciam.com/article.cfm?chanID=sa006&colID=1&articleID= 000479CD-F58C-11BE-
AD0683414B7F0000
 Vittorio, Salvatore. "Quantum Cryptography: Privacy through Uncertainty." CSA. October 2002.
http://www.csa.com/discoveryguides/crypt/overview.php
 "Quantum Cryptography Tutorial." Dartmouth College. http://www.cs.dartmouth.edu/~jford/crypto.html