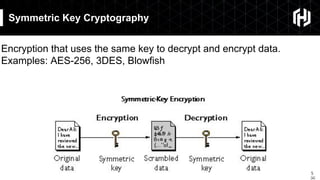
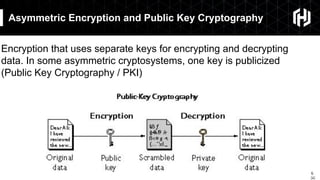
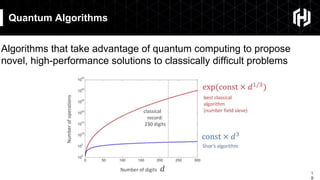
The document discusses the impact of quantum computing on cryptography, emphasizing the threats posed by quantum algorithms like Shor's and Grover's that can significantly weaken existing encryption methods, particularly asymmetric cryptography. It highlights the need for new quantum-secure cryptographic standards and the importance of adapting symmetric key cryptography to longer key lengths to enhance security. Additionally, quantum cryptography techniques like Quantum Key Exchange and the potential for new cryptographic mechanisms are introduced as advancements in safeguarding data.

1. Quantum Cryptography
Opportunities and Threats in Quantum Computing

2. Agenda
1. Introduction to Cryptologic Terminology
2. Introduction to Quantum Mechanics and Quantum Computing
3. Quantum Cryptanalysis
4. Quantum Cryptography
5. Conclusions

3. Cryptologic Terminology

4. 4

Protecting Data
Basic Terminology
Cryptography / Encryption: Writing and reading encoded data
Cryptology (“Crypto”): Study of encryption and decryption
Key: Sensitive element to decrypt a message
Encryption Terminology
Ciphertext: Result of passing a secret through a cipher
Plaintext / Cleartext: Decrypted secret protected by a cipher
E(Data = “ABC”, Key = “123”) = 0x566030c4
E(Data = “ABC”, Key = “123”) = 0x566030c4

5. 5

Symmetric Key Cryptography
Encryption that uses the same key to decrypt and encrypt data.
Examples: AES-256, 3DES, Blowfish

6. 6

Asymmetric Encryption and Public Key Cryptography
Encryption that uses separate keys for encrypting and decrypting
data. In some asymmetric cryptosystems, one key is publicized
(Public Key Cryptography / PKI)

7. 7

Cryptographic Hash Algorithms
One way encoding that maps data of varying size to a fixed size string
while minimizing collisions (when 2 hashes of different input are the
same)
Examples: SHA-256, BLAKE

8. 8

Side Channel Attacks - Go Around the Math
Breaking encryption by attacking the implementation of a cipher or
stealing data before it can enter the cipher

9. 9

Cryptanalysis - Break Through the Math
Breaking encryption by using mathematical analysis or advanced
computing for reducing the difficulty of guessing ciphertext or key

10. Quantum Mechanics and
Quantum Computing

11. 1
1
Quantum Superposition and Entanglement
Superposition: The quantum state of a subatomic particle is a
function of the interaction of its components.
Entanglement: When two quantum particles meet or are created in
such a way that their state is inseparable (position of one is a
function of the position of another - coherance)
Example: When two waves collide, the
geometry of one wave is a function of the
other wave’s collision

12. 1
2
Observer Effect and Quantum Uncertainty
Two key properties distinguish quantum mechanics from classical
mechanics
Quantum Uncertainty: We can’t directly observe the exact position
and velocity of a quantum particle. Quantum states are probabilistic
and cover a spread of possibilities (a PDF) with position determined
by statistical analysis of a result (expected value of the PDF).
Observer Effect: When we measure a quantum system we break its
coherence and have to start over.

13. 1
3
Qubits: The Basic Unit of Quantum Computing
A qubit is a quantum version of the bit used in digital computing. It
contains two base states of 0 and 1, but due to superposition and
quantum mechanics an array of n-qubits can simultaneously
represent 2^n states

14. 1
4
Quantum Logic Gates (QLGs)
Like logic gates that run digital circuits, quantum logic gates simulate boolean logic
that can be used to evaluate expressions by forcing interactions between qubits to
make them coherent.
Most QLGs rely on the measured interaction of lasers in an isolated, measurable
environment. Data sent through QLGs is lossless and moves at the speed of light.

15. 1
5
Problems with QLGs: Measurement and Error
Unfortunately constructing QLGs is hard:
Isolation: Other factors may impact a quantum system and
decohere its QLGs
Uncertainty: Never know the explicit state of a qubit, only a range of
potential results
Observer Effect: Once a QLG is measured, it is docherent

16. 1
6
Why Computing on QLGs is Hard
Quantum computing is like measuring
the brief rise in water levels in a small
puddle when two pebbles fall in
simulteanously...
...at night, by hand with a tape measure,
during a typhoon.

17. 1
7
Quantum Computers and Quantum Computing (QC)
Assemblies of quantum logic gates that can evaluate the results of
qubit interactions
Solves some problems faster than classical
computers via quantum parallelism:
exploiting superposition and entanglement
to run calculations across an array of gates
simultaneously
Very hard and expensive to build/run due
to measurement and error issues.

18. 1
8
Quantum Algorithms
Algorithms that take advantage of quantum computing to propose
novel, high-performance solutions to classically difficult problems

19. Quantum Cryptanalysis

20. 2
0
Shor’s Algorithm
Significantly reduces the difficulty of factoring large prime numbers

21. 2
1
Grover’s Algorithm
Reduces the difficulty in searching for the unique input of a “black
box” function that produces a given output (linear to sub-linear time)

22. 2
2
QC Risks for Existing Cryptography
Type of Cryptography Risk from QC Response
Cryptographic Hashes
Low: Grover’s Algorithm
moderately speeds up pre-image
attacks to search for hashes
No serious risk due to anti-collision
size protections in cyptographic
hashes. Some cryptocurrencies will
need to change their mining
algorithms (e.g.: Proof of Work)
Symmetric Crypto
Moderate: Grover’s Algorithm
speeds up brute force attacks
Double bit length of all symmetric
key cryptography
Asymmetric Crypto (PKI)
Very High: Shor’s Algorithm makes
integer factorization computationally
easy, invalidating the security of
most asymmetric crypto and PKI
Develop new PKI algorithms that
are quantum-secure (i.e.:
post-quantum cryptography)

23. 2
3
Changes to FIPS 140-2 due to Quantum Computing
NIST has begun a Post Quantum
Cryptography Standardization program to
introduce new cryptographic standards to
FIPS 140-2
Currently reviewing alternatives to RSA,
ECDSA, and Diffie-Hellman
Planned draft changes to FIPS 140-2
beginning in 2022

24. Quantum Cryptography

25. 2
5
Quantum Key Exchange (QKE)
Comprise a symmetric key for use between two parties by entangling
arrays of matching qubits and performing operations on the coherent
systems. Eavesdropping the system breaks coherence.
QKE implemented in CN/AUS satellite system in 2018

26. 2
6
Quantum Coin Flipping
Zero-trust system for “cryptographic escrow” where two parties can create
a self-certifying ledger of transactions that, once mutually verified, creates
a shared key or secret.
Lossless transmission
Detects eavesdropping
Certifiable by both parties
Very hard to implement

27. Conclusions

28. 2
8
TL;DR
We need new asymmetric cryptography / PKI
Quantum computing algorithms threaten prime factorization-based cryptography like
RSA and Diffie-Hellman, as well as cryptographic hash algorithms based on PKI
We need to increase key length for symmetric key crypto
Grover’s Algorithm requires us to double the key length for symmetric key
cryptography like AES (as well as some cryptographic hash algorithms)
...but this is not the “cryptopocalypse”
Not all cryptography is rendered insecure by QC (example: hashing) and new
methods for safeguarding data are provided by advances in quantum computing