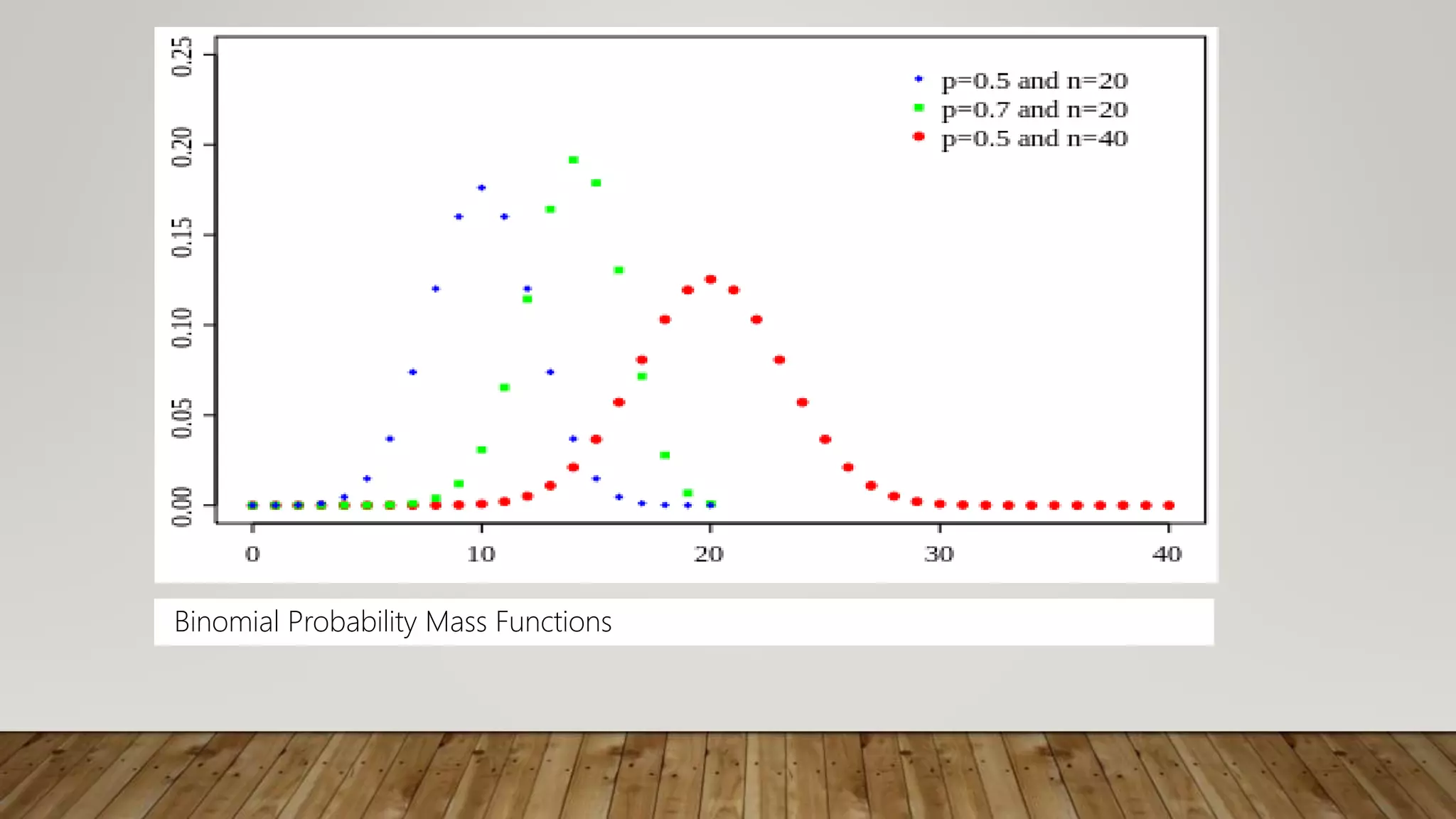
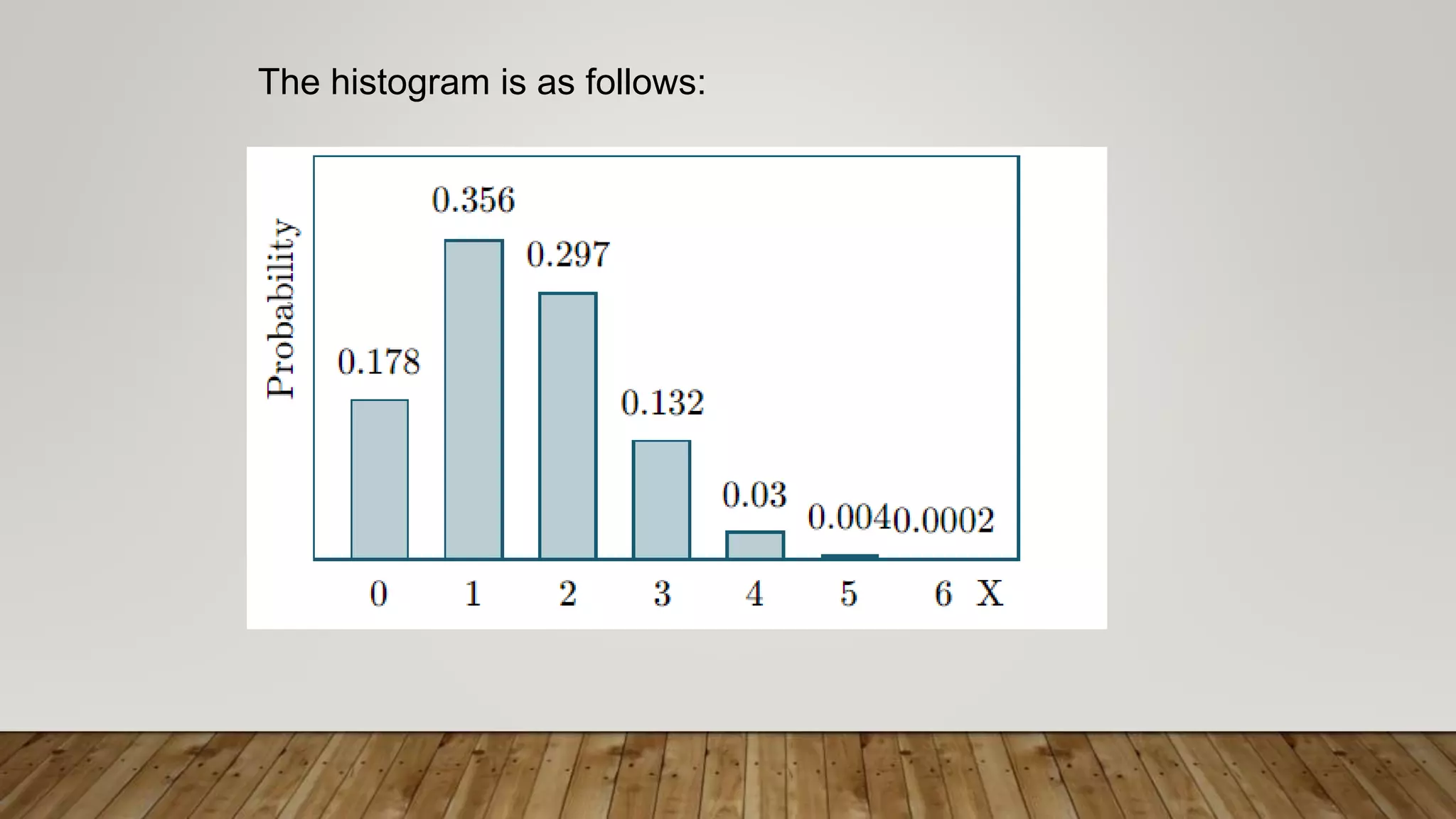
The document discusses binomial distributions, which model outcomes that can be classified as successes or failures, with a constant probability of success for each trial. A binomial distribution is defined by the number of trials (n) and the probability of success (p) for each trial. The mean is np and the standard deviation is npq. Examples are given of calculating binomial probabilities, such as the probability of a certain number of patients recovering from a disease out of a sample size.

1. BINOMIAL
DISTRIBUTION
THE BINOMIAL DISTRIBUTION IS A
DISCRETE DISTRIBUTION.

2.  The Binomial is type of distribution that has two possible
outcomes.
 It is applicable to Discrete random variables only.
 A binomial distribution can be thought of as simply the
probability of a SUCCESS or FAILURE outcome in an
experiment or survey that is repeated multiple times.

3. Binomial Probability Mass Functions

4. Binomial distribution experimental
conditions.
Each trial results in two mutually disjoint outcomes
termed as success and failure.
The number of trials is ‘n’ finite.
The trials are independent of each other.
The probability of success ‘p’ is constant for each trial.

5. .
Geometric Distribution
In a series of Bernoulli trials (independent trials with constant probability p of
a success), the random variable X that equals the number of trials until the
first success is a geometric random variable with parameter 0 < p < 1
f (x) = (1 − p) x-1 p x= 1, 2,…
Example- The probability that a bit transmitted through a digital
transmission
channel is received in error is 0.1. Assume that the transmissions are
independent events, and let the random variable X denote the number of bits
transmitted until the first error. Then P(X = 5) is the probability that the first
four bits are transmitted correctly and the fifth bit is in error
P(X = 5) = P(OOOOE) = 0.9^4(0.1) = 0.066

6. 𝑃(𝑋 = 𝑟) =
𝑛!
𝑟! (𝑛 − 𝑟)!
𝑝 𝑟
𝑞 𝑛−𝑟
n=Number of trials
p=Probability of Success
q=Probability of Failure(1-P)

7. Mean and Standard Deviation
The mean (expected value) of a binomial random
variable is
The standard deviation of a binomial random variable
is
np
npq

8. Example1. A Hospital records show that of patients suffering from a
certain disease %75% die of it. What is the probability that of
6 randomly selected patients,4 will recover?
This is a binomial distribution because there are only 2 outcomes (the
patient dies, or does not).
Let X = number who recover.
Here, n=6 and x=4.
Let p=0.25 (success, that is, they live),
q=0.75 (failure, i.e. they die).
The probability that 4 will recover:

10. The histogram is as follows:

11. It means that out of the 6 patients chosen, the
probability that:
None of them will recover is 0.17798,
One will recover is 0.35596, and
All 6 will recover is extremely small.

12. Example 2.
Ten percent of computer parts produced by a certain supplier are
defective. What is the probability that a sample of 10 parts contains
more than 3 defective ones?

13. Thank You