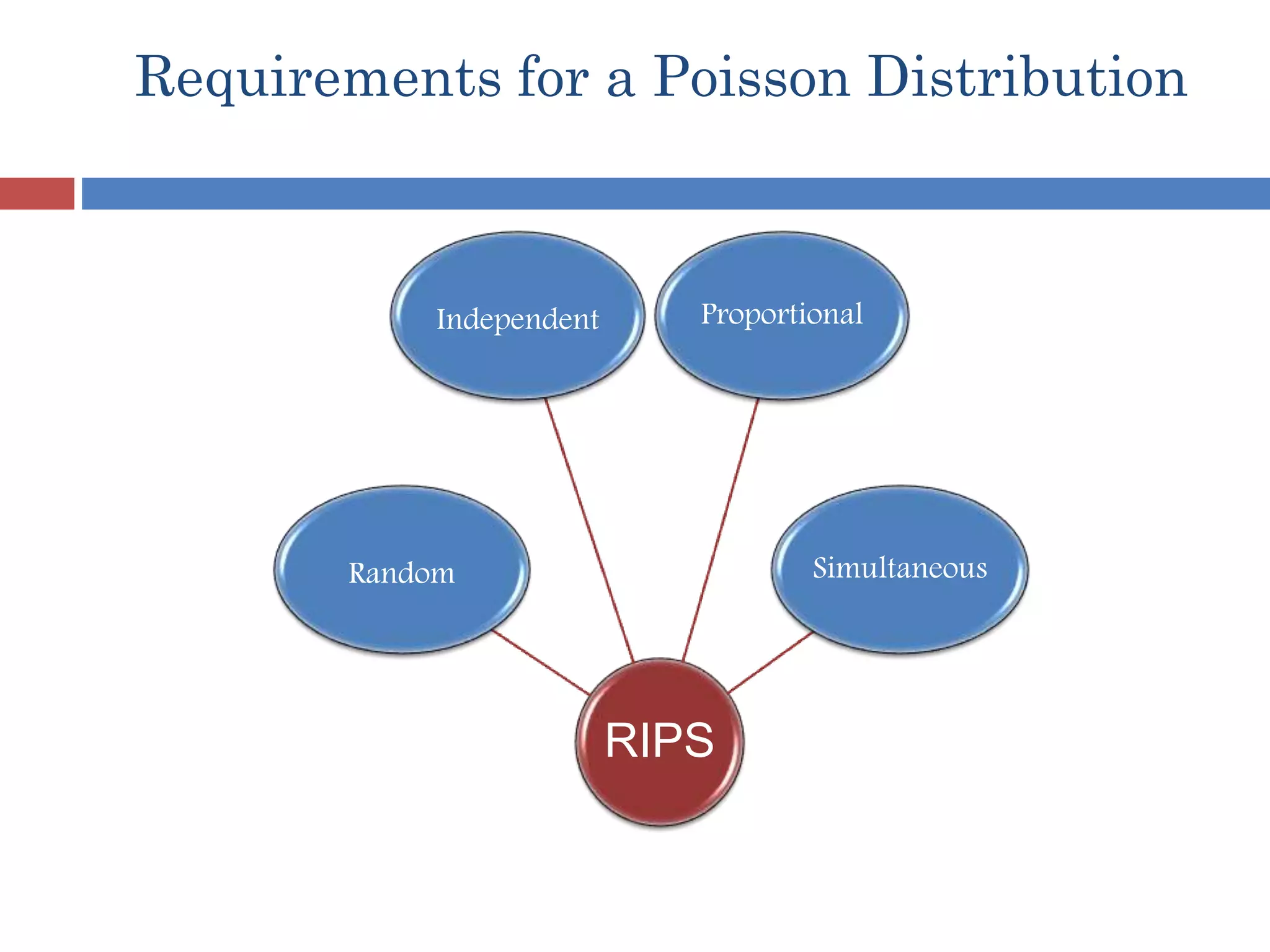
The document presents an overview of the Poisson distribution, a discrete probability distribution established by Simeon Denis Poisson in 1837, characterized by the mean number of occurrences within a specified time interval. It applies to scenarios where events are rare and independent, such as the number of earthquakes per year, and includes assumptions like constant probability across intervals. Mathematical calculations for mean and variance are included, alongside examples of accident probabilities based on average occurrences.

2. Presentation
on
Poisson Distribution-Assumption , Mean & Variance

3.  A discrete Probability Distribution
 Derived by French mathematician Simeon Denis
Poisson in 1837
 Defined by the mean number of occurrences in a
time interval and denoted by λ
 Also known as the Distribution of Rare Events
Poisson Distribution
Simeon D. Poisson (1781-
1840)

4. Works when binomial calculation becomes impractical (No. of
trials>probability of success),
 Applied where random events in space or time are expected to occur.
 Deviation indicates some degree of non-randomness in the events
Example: Number of earthquakes per year.
Cont’d…

5. Requirements for a Poisson Distribution
RIPS
Random
Proportional
Simultaneous
Independent

6. Assumptions
 The probability of occurrence of an event is constant for
all subintervals:
 There can be no more than one occurrence in each
interval
 Occurrence are independent .

7. 



])[(
onDistributiyProbabilitPoissonofVariance
)(
onDistributiyProbabilitPoissonofMean
22
XE
XE
x
x
If the Poisson variable X, then by the formula: P(X = x) = e
x
x!
Mean and Variance

8. Mathematical Calculations
#If the average number of accidents at a particular intersection in
every year is 18. Then-
(a) Calculate the probability that there are exactly 2 accidents
occurred in this month.
(b) Calculate the probability that there is at least one accident
occurred in this month.

9. There are 12 months in a year, so  = 12
18
= 1.5 accidents per month
P(X = 3) =
!x
e x

!2
5.1 25.1

e
= 0.2510
(a) Calculate the probability that there are exactly 2
accidents occurred in this month.

10. (b) Calculate the probability that there is at least one
accident occurred in this month.
P(X ≥ 1 ) = P(X=1) + P(X=2) + P(X=3) + …. Infinite.
So… Take the complement: P(X=0)
!x
e x


!0
5.1 05.1

e
5.1
 e
= 0.223130…