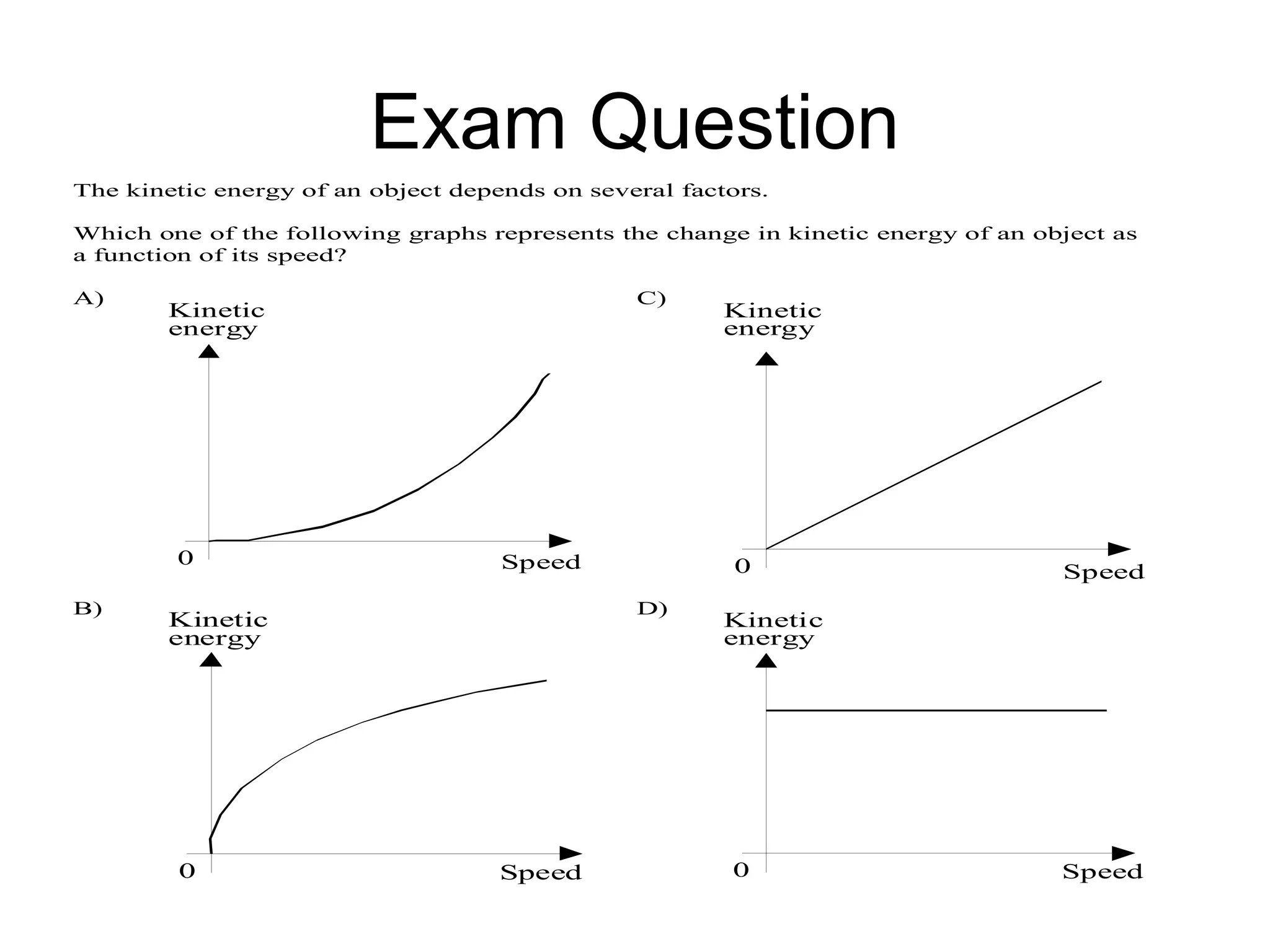
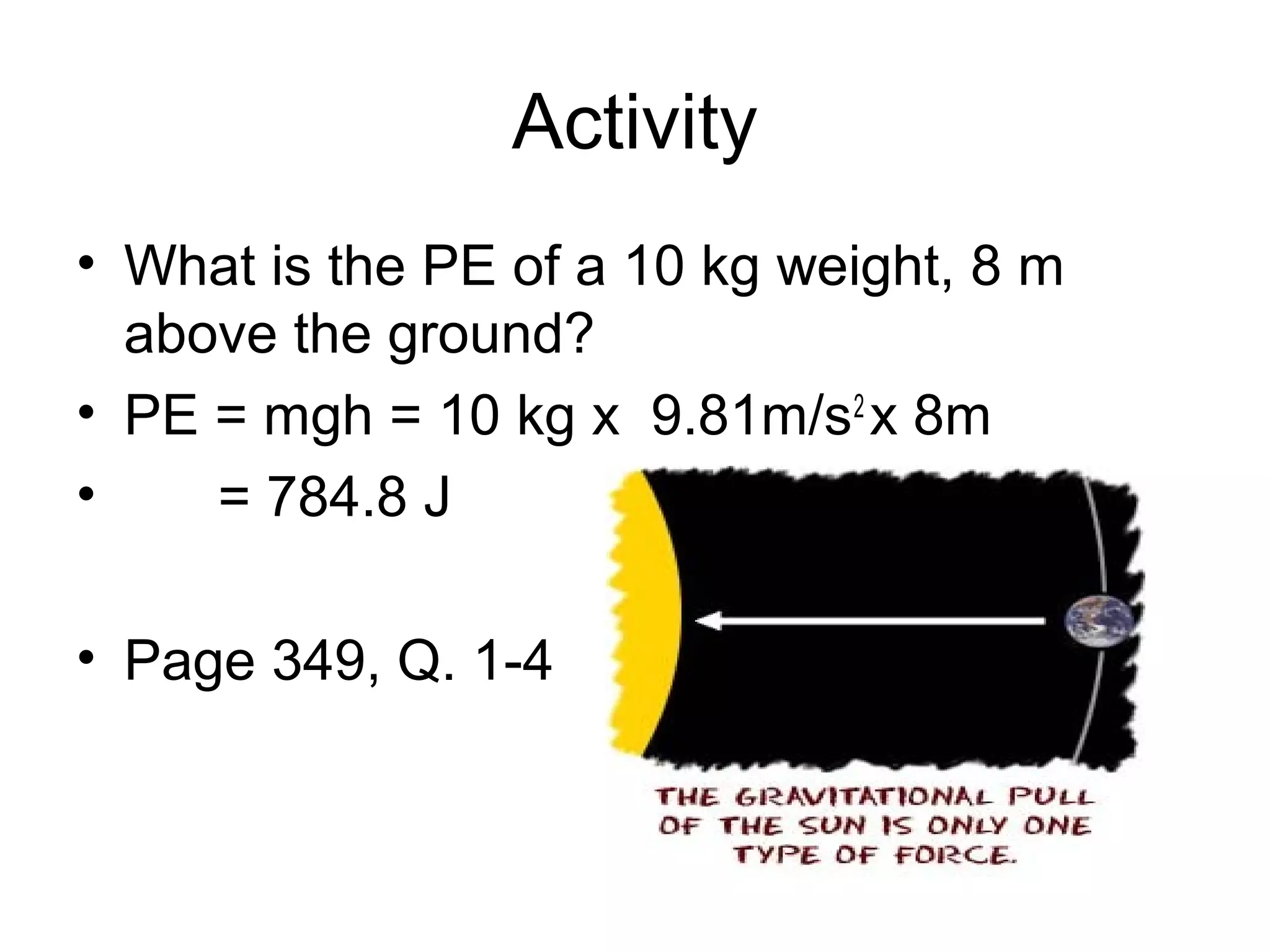
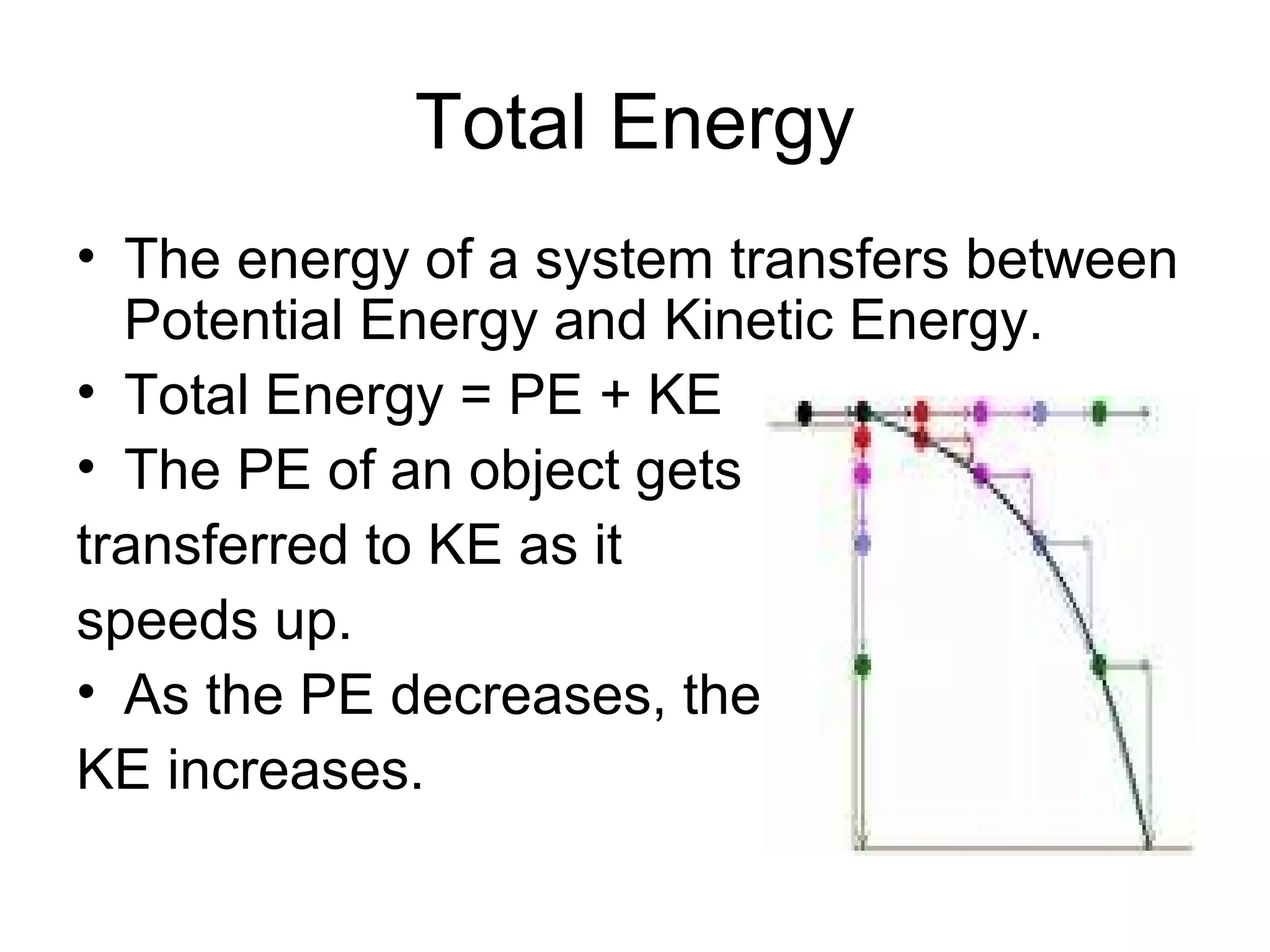
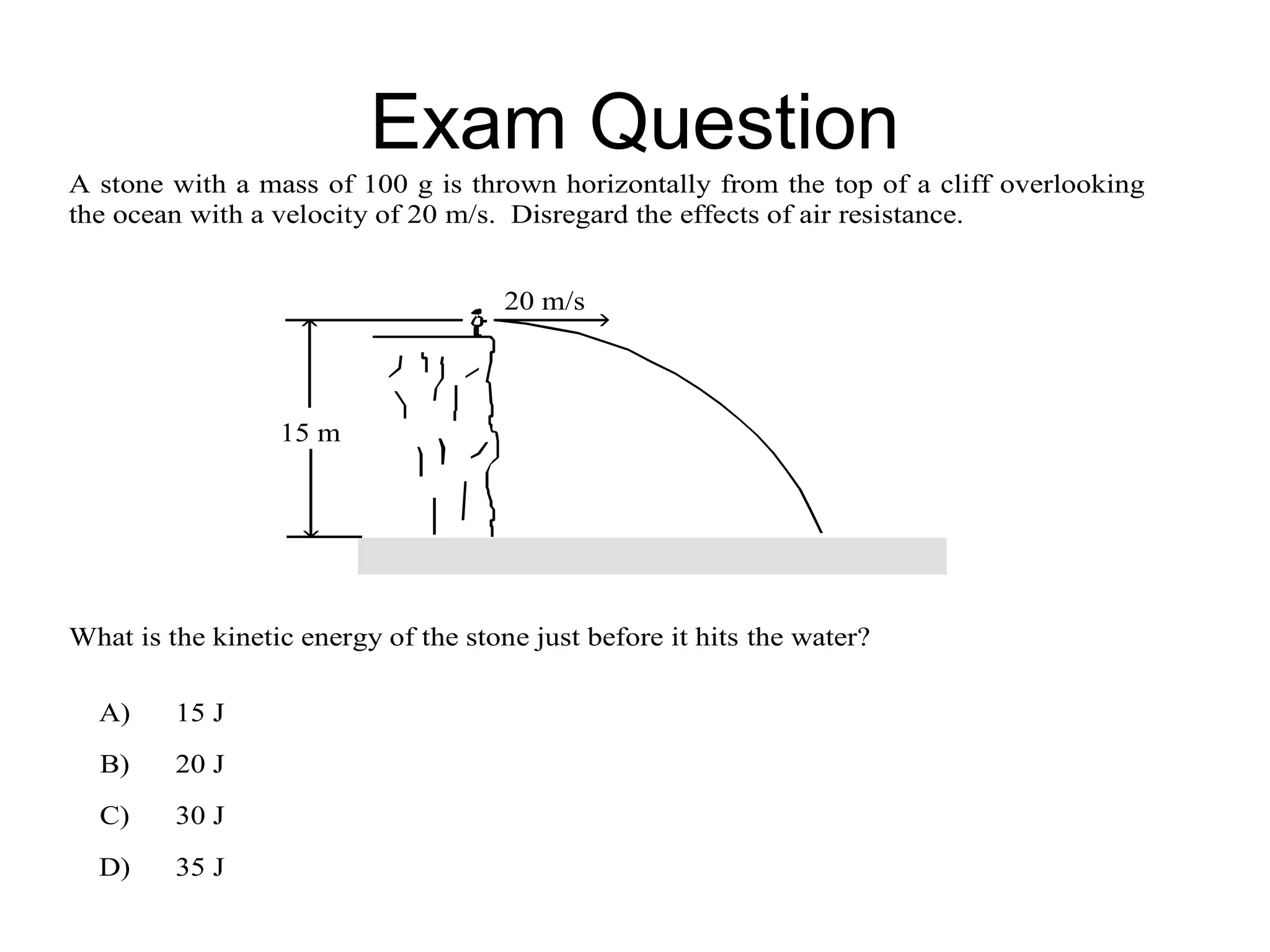
The document discusses different types of energy including kinetic, potential, elastic, chemical, and nuclear energy. It provides formulas for calculating kinetic energy as 1/2mv^2 and potential energy as mgh. The document also explains how the total energy of a system is conserved as energy is transferred between potential and kinetic forms.

1. Mechanical Energy
Chapter 16/17

2. Kinds of Energy
• Gravitational Potential Energy: due to position
• Kinetic Energy: due to motion
• Heat Energy: due to movement of heat energy
from regions of high energy to areas of low
energy.
• Radiant Energy: due to light
• Chemical Potential Energy: due to bonds
• Elastic Energy: stressed objects that return to
their original shape.
• Electrical Energy: due to movement of electrons
• Nuclear Energy: due to atomic fission/fusion

3. Kinetic Energy
• Kinetic Energy is the energy an object has
due to its motion.
• Kinetic energy is the energy of a moving
object.
• The KE depends on the mass and the
speed.
• Ek, KE= ½ mv2, unit is Joule, J
• m is mass in kg, v is velocity in m/s

4. Activity
• What is the KE of a 6 kg curling stone
moving at 4 m/s?
• KE = ½ mv2
• = ½ x 6kg x (4 m/s)2
• = ½ x 6 x 16
• = 48 J
• Do page 341, Q. 1- 4

5. Exam Question
The kinetic energy of an object depends on several factors.
Which one of the following graphs represents the change in kinetic energy of an object as
a function of its speed?
A) C)
Kinetic Kinetic
energy energy
0 Speed 0 Speed
B) D)
Kinetic Kinetic
energy energy
0 Speed 0 Speed

6. Exam Question
An car, travelling along a horizontal road, has kinetic energy of 1.6 × 106J.
The driver slows the car to half of its original speed.
What is the new kinetic energy of the car?
A) 1.6 × 106 J
B) 8.0 × 105 J
C) 4.0 × 105 J
D) 1.6 × 105 J

7. Activity
• Page 341, Q 1 - 6

8. Potential Energy
• If we put work into an object (W=FΔd) by
lifting it up against gravity, it now has the
ability to move; it has the potential to fall
down and use up the energy we put into it.
• W = FΔd = mgd
• Ep , PE = mgh, unit is Joules, J
• m is the mass in kg
• g is the acceleration due to gravity
• h is the height above the Earth’s surface, m.

9. Activity
• What is the PE of a 10 kg weight, 8 m
above the ground?
• PE = mgh = 10 kg x 9.81m/s2 x 8m
• = 784.8 J
• Page 349, Q. 1-4

10. Exam Question
A weather balloon with a mass of 4.0 kg, including the weather instruments, rises
vertically in the air. It passes an altitude of 200 metres at a velocity of 2.0 m/s.
2.0 m/s
200 m
At this point what is its potential energy with respect to the ground?
A) 8.0 × 103 J
B) 8.0 × 102 J
C) 8.0 × 101 J
D) 8.0 J

11. Total Energy
• The energy of a system transfers between
Potential Energy and Kinetic Energy.
• Total Energy = PE + KE
• The PE of an object gets
transferred to KE as it
speeds up.
• As the PE decreases, the
KE increases.

12. Total Energy
• What is the speed of a 500g rock that
drops from a height of 78.4 m, just before
it hits the ground?
• ET = KE + PE, at first, v = 0 m/s
• = ½ mv2 + mgh, since v = 0, KE = 0
• = 0.5kgx9.81m/s2x78.4m, ET = PE only
• = 384.6 J
• As the rock approaches the ground all its
PE is transferred to KE, so PE = 0. So…

13. Total Energy, Part Deux
• ET = PE + KE
• 384.6 J = KE
• 384.6 = ½ mv2
• 384.6 = 1/2x 0.5kg x v2
• 1538.4 J = v2
• v = 39.2 m/s
• So just before it hits the ground, the rock
has a speed of 39.2 m/s

14. Another way to solve it
• Same situation, just look at the speed and
distance.
• We could use v2 = u2 + 2as
• = 02 + 2(9.81)(78.4)
• = 1538
• So, v = 39.2 m/s
• Both methods work, depending on the
information given.
• Page 353, Q. 2-5
• Page 356, Q. 6

15. Exam Question
A small airplane with a mass of 1000 kg, is flying at 60 m/s at an altitude of 250 m.
60 m/s
250 m
What is the total mechanical energy of this airplane with respect to the ground?
A) 1.8 × 106 J
B) 2.5 × 106 J
C) 4.3 × 106 J
D) 6.1 × 106 J

16. Exam Question
A golf ball is dropped out of a window which is 10 m above the ground. The ball has a
mass of 50 g. Disregard the effects of air resistance.
10 m
What is the kinetic energy of the ball just before it hits the ground?
A) 10 J
B) 7.5 J
C) 5.0 J
D) 2.5 J

17. Exam Question
A stone with a mass of 100 g is thrown horizontally from the top of a cliff overlooking
the ocean with a velocity of 20 m/s. Disregard the effects of air resistance.
20 m/s
15 m
What is the kinetic energy of the stone just before it hits the water?
A) 15 J
B) 20 J
C) 30 J
D) 35 J

18. Exam Question
A 100 g ball is thrown vertically upward from the ground with a velocity of 20 m/s.
Disregard the effects of air resistance.
What is the kinetic energy of this ball after it has risen 5.0 metres?
A) 20 J
B) 15 J
C) 10 J
D) 5.0 J

19. Summary
• Energy is the ability to do work.
• Work is the transfer of energy. (W=ΔE)
• Friction often does negative work on an
object because it removes energy from it.
• Gravitational Potential Energy is the
energy of an object due to its height above
the Earth’s surface. PE = mgh
• Kinetic Energy is the energy of a moving
object. KE = ½ mv2

20. Summary
• The Law of Conservation of Energy states that in
any transfer or transformation of energy, the
total amount of energy remains the same.
• The form of the energy may be changed, e.g.
noise, heat, vibration, friction.
• In situations where friction and air resistance are
small enough to be ignored, and where no other
energy is added to the system, the total
mechanical energy is conserved.

21. Summary
• E total = KE + PE (before) = KE + PE (after)
• Heat is the measure of the amount of
thermal energy that flows from one body
to another because of a difference in
temperature.
• Work done on an object can cause an
increase in the temperature of an object.

22. Exam Question
The starter motor of a car is not working. One person stays in the car while the other
pushes it from behind to get it up to a certain speed so that it can be started. The car and
the person inside it have a total mass of 1.00 × 103 kg. Disregard the effects of friction.
The car is at a complete stop. The person who pushes it exerts a force of
2.00 × 102 newtons for 15.0 seconds.
How much kinetic energy does the car gain as a result of the push?
A) 1.80 × 104 J
B) 1.35 × 104 J
C) 9.00 × 103 J
D) 4.50 × 103 J

23. Activity
• Page 361, Q. 1-7

24. Elastic Potential Energy
• We know Hooke’s Law – F = kx
– k – spring constant, N/m
– x – elongation of the spring, m
• The energy stored in a spring.
• E PE = ½ k (x)2

25. Activity
• The length of a compressed spring,
unextended, is compressed by 5 cm,
using a force of 20 N. Calculate the
energy stored in the spring.
• Using F = kx
• 20 = k (0.05 m)
• k = 400 N/m

26. Continued
• E PE = ½ k (x)2
• = ½ (400) (0.05) 2
• = 0.5 J
• Do Page 373, Q 1-3.