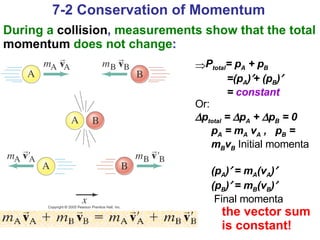
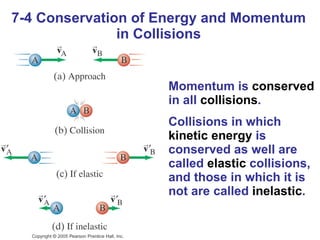
1. Chapter 7 discusses linear momentum and its relationship to force, conservation of momentum during collisions, and the conservation of energy and momentum in elastic and inelastic collisions. 2. Momentum is defined as mass times velocity (p=mv) and changes due to an applied net force according to Newton's Second Law (Δp/Δt=F). 3. During collisions, the total momentum of an isolated system remains constant due to the conservation of momentum, which can be used to analyze collisions.

1. Chapter 7 Linear Momentum

2. Units of Chapter 7 Momentum and Its Relation to Force Conservation of Momentum Collisions and Impulse Conservation of Energy and Momentum in Collisions Elastic Collisions in One Dimension Inelastic Collisions Center of Mass (CM)

3. Momentum is a vector symbolized by the symbol p , and is defined as p = mv (a vector || v ) SI Units: kg  m/s = N  s Question: How is the momentum of a body change? Chapter 7 Linear Momentum Answer: By the application of a force F (7-1)

4. Momentum: p = mv The rate of change of momentum is equal to the net force : ∑F =  p/  t Also considered as the most general statement of Newton’s 2nd Law Is more general than ∑F = ma because it allows for the mass m to change with time also! Example , rocket motion! Later! 7-1 Momentum and Its Relation to Force (7-2)

5. 7-1 Momentum and Its Relation to Force Newton’s 2nd Law (General Form!) ∑ F =  p/  t Note: if m is constant, becomes: ∑ F =  p/  t =  (mv)/  t = m(  v/  t) = ma m = constant. Initial momentum p 0 = mv 0 , Final momentum p = mv . becomes: ∑ F =  p/  t = m(v-v 0 )/  t = m(  v/  t) = ma (as before)

6. ∑ F =  p/  t Initial p = mv Final p = 0 Water rate = 1.5 kg/s  p = 0 – mv F = (  p/  t) = [(0-mv)/  t] = - mv/  t m = 1.5 kg every second On the water F = -30 N On the car F = 30 N Example 7-2

7. Experimental fact (provable from Newton’s Laws): For two colliding objects, (zero external force) the total momentum is conserved (constant) throughout the collision The total (vector) momentum before the collision = the total (vector) momentum after the collision. Law of Conservation of Momentum 7-2 Conservation of Momentum

8. 7-2 Conservation of Momentum During a collision , measurements show that the total momentum does not change : P total = p A + p B =(p A )  + (p B )  = constant Or:  p total =  p A +  p B = 0 p A = m A v A , p B = m B v B Initial momenta (p A )  = m A (v A )  (p B )  = m B (v B )  Final momenta the vector sum is constant!

9. Collision: m 1 v 1 +m 2 v 2 = m 1 (v 1 )  + m 2 (v 2 )  Proof, using Newton’s Laws: Force on 1, due to 2, F 12 =  p 1 /  t = m 1 [(v 1 )  - v 1 ]/  t Force on 2, due to 1, F 21 =  p 2 /  t = m 2 [(v 2 )  - v 2 ]/  t Newton’s 3 rd Law : F 21 = - F 12  - m 1 [(v 1 )  - v 1 ]/  t = m 2 [(v 2 )  - v 2 ]/  t OR: m 1 v 1 +m 2 v 2 = m 1 (v 1 )  + m 2 (v 2 )   Proven ! A ->1 B->2

10. 7-2 Conservation of Momentum More formally, the law of conservation of momentum states: The total momentum of an isolated system of objects remains constant .

11. m 1 v 1 +m 2 v 2 = (m 1 + m 2 )V  v 2 = 0, (v 1 )  = (v 2 )  = V   V  = [(m 1 v 1 )/(m 1 + m 2 )] = 12 m/s Example 7-3 Initial Momentum = Final Momentum (1D)

12. 7-2 Conservation of Momentum Momentum conservation works for a rocket as long as we consider the rocket and its fuel to be one system, and account for the mass loss of the rocket. 0 = P rocket - P gas

13. Momentum Before = Momentum After m 1 v 1 +m 2 v 2 = m 1 (v 1 )  + m 2 (v 2 )  m B = 0.02 kg m R = 5.0 kg (v B )  = 620 m/s 0 = m B (v B )  + m R (v R )   (v R )  = - 2.5 m/s (to left, of course!) Example 7-4

14. 7-3 Collisions and Impulse During a collision, objects are deformed due to the large forces involved. Since , we can write The definition of impulse: (7-5)

15. 7-3 Collisions and Impulse Since the time of the collision is very short, we need not worry about the exact time dependence of the force, and can use the average force . Impulse here is the area under the F c vs. t curve.

16. 7-3 Collisions and Impulse The impulse tells us that we can get the same change in momentum with a large force acting for a short time, or a small force acting for a longer time. This is why you should bend your knees when you land; why airbags work; and why landing on a pillow hurts less than landing on concrete .

17. Advantage of bending knees when landing! a) m =70 kg, h =3.0 m Impulse:  p = ? F  t=  p = m(0-v) First, find v (just before hitting):  KE +  PE = 0 (½)m(v 2 -0) + mg(0 - h) = 0  v = 7.7 m/s Or using: Impulse:  p = -540 N s Example 7-6

18. Advantage of bending knees when landing! Impulse:  p = -540 N s m =70 kg, h =3.0 m, F = ? b) Stiff legged: v = 7.7 m/s to v = 0 in d = 1 cm ( 0.01m )! average v = (½ )(7.7 +0) = 3.8 m/s Time  t = d/v = 2.6  10 -3 s F = |  p/  t| = 2.1  10 5 N (Net force upward on person) From free body diagram, F = F grd - mg  2.1  10 5 N Enough to fracture leg bone!!! Example 7-6

19. Example 7-6 Advantage of bending knees when landing! Impulse:  p = -540 N s m =70 kg, h =3.0 m, F = ? c) Knees bent: v = 7.7 m/s to v = 0 in d = 50 cm ( 0.5m ) v = (½ )(7.7 +0) = 3.8 m/s Time  t = d/v = 0.13 s F = |  p/  t| = 4.2  10 3 N (Net force upward on person) From free body diagram, F = F grd - mg  4.9  10 3 N Leg bone does not break!!!

20. Impulse: m = 0.060 kg v = 25 m/s  p = change in momentum  wall. Momentum || to wall does not change.  Impulse will be  wall. Take + direction toward wall, Impulse =  p = m  v = m[(- v sin θ ) - (v sin θ )] = -2mv sin θ = - 2.1 N s. Impulse on wall is in opposite direction: 2.1 N s . Problem 17 v i = v sin θ v f = - v sin θ

21. Momentum is ALWAYS (!!!) conserved in a collision!  m 1 v 1 + m 2 v 2 = m 1 (v 1 )  + m 2 (v 2 )  HOLDS for ALL collisions ! For Elastic Collisions ONLY (!!) Total Kinetic energy ( KE ) is conserved !! ( KE) before = (KE) after  (½)m 1 (v 1 ) 2 + (½) m 2 (v 2 ) 2 = (½)m 1 (v 1  ) 2 + (½)m 2 (v 2  ) 2 7-4 Conservation of Energy and Momentum in Collisions

22. 7-4 Conservation of Energy and Momentum in Collisions Momentum is conserved in all collisions . Collisions in which kinetic energy is conserved as well are called elastic collisions, and those in which it is not are called inelastic .

23. 7-5 Elastic Collisions in One Dimension Here we have two objects colliding elastically . We know the masses and the initial speeds. Since both momentum and kinetic energy are conserved, we can write two equations. This allows us to solve for the two unknown final speeds.

24. Special case : Head-on Elastic Collisions. Momentum is conserved ( ALWAYS !) P before = P after m 1 v 1 + m 2 v 2 = m 1 v 1  + m 2 v 2  v 1 , v 2 , v 1  , v 2  are one dimensional vectors! Kinetic Energy is conserved ( ELASTIC !) (KE) before = (KE) after (½)m 1 (v 1 ) 2 + (½)m 2 (v 2 ) 2 = (½)m 1 (v 1  ) 2 + (½) m 2 (v 2  ) 2 2 equations, 6 quantities: v 1 ,v 2 ,v 1  , v 2  , m 1 ,m 2  Clearly, must be given 4 out of 6 to solve problems! Solve with CAREFUL algebra!!

25. m 1 v 1 + m 2 v 2 = m 1 v 1  + m 2 v 2  (1) (½)m 1 (v 1 ) 2 + (½)m 2 (v 2 ) 2 = (½)m 1 (v 1  ) 2 + (½) m 2 (v 2  ) 2 (2) Now, some algebra with (1) & (2 ), the results of which will help to simplify problem solving : Rewrite (1) as: m 1 (v 1 - v 1  ) = m 2 (v 2  - v 2 ) (a) Rewrite (2) as: m 1 [(v 1 ) 2 - (v 1  ) 2 ] = m 2 [(v 2  ) 2 - (v 2 ) 2 ] (b) Divide (b) by (a):  v 1 + v 1  = v 2 + v 2  or v 1 - v 2 = v 2  - v 1  = -(v 1  - v 2  ) (3) Relative velocity before= - Relative velocity after Elastic head-on (1d) collisions only!!

26. Summary: 1d Elastic collisions: Rather than directly use momentum conservation + KE conservation, often convenient to use: Momentum conservation: m 1 v 1 + m 2 v 2 = m 1 v 1  + m 2 v 2  (1) along with: v 1 - v 2 = v 2  - v 1  = -(v 1  - v 2  ) (3) (1) & (3) are equivalent to momentum conservation + KE conservation, since (3) was derived from these conservation laws!

27. m 1 = m 2 = m, v 1 = v, v 2 = 0, v 1  = ?, v 2  = ? Momentum Conservation: mv +m(0)=mv 1  +mv 2  Masses cancel  v +0 = v 1  + v 2  (I) Relative velocity results for elastic head on collision: v 1 - v 2 = v 2  - v 1   v - 0 = v 2  - v 1  (II) Solve (I) & (II) simultaneously for v 1  & v 2  :  v 1  = 0, v 2  = v Ball 1: to rest. Ball 2 moves with original velocity of ball 1 Example 7-7: Pool (Billiards)

28. 7-6 Inelastic Collisions With inelastic collisions, some of the initial kinetic energy is lost to thermal or potential energy. It may also be gained during explosions , as there is the addition of chemical or nuclear energy. A completely inelastic collision is one where the objects stick together afterwards, so there is only one final velocity.

29. Momentum Conservation mv = (m + M)v ´ Energy Conservation (½)(m +M)(v´) 2 = (m + M)gh v´= (2gh)½  v = [1 +(M/m)](2gh) ½ Ex. 7-10 & Prob. 32 (Inelastic Collisions)

30. Up to now, we’ve been mainly concerned with the motion of single (point) particles. To treat extended bodies, we’ve approximated the body as a point particle & treated it as if it had all of its mass at a point! How is this possible? Real, extended bodies have complex motion, including (possibly): translation, rotation, & vibration! 7-8 Center of Mass

31. 7-8 Center of Mass In (a), the diver’s motion is pure translation ; in (b) it is translation plus rotation . There is one point that moves in the same path a particle would take if subjected to the same force as the diver. This point is called the center of mass ( CM ).

32. 7-8 Center of Mass The general motion of an object can be considered as the sum of the translational motion of the CM , plus rotational , vibrational , or other forms of motion about the CM.

33. 7-8 Center of Mass For two particles, the center of mass lies closer to the one with the most mass: where M is the total mass.

34. 7-8 Center of Mass The center of gravity is the point where the gravitational force can be considered to act. It is the same as the center of mass as long as the gravitational force does not vary among different parts of the object.

35. 7-8 Center of Mass The center of gravity can be found experimentally by suspending an object from different points. The CM need not be within the actual object – a doughnut’s CM is in the center of the hole.

36. Summary of Chapter 7 Momentum of an object: Newton’s second law: Total momentum of an isolated system of objects is conserved. During a collision, the colliding objects can be considered to be an isolated system even if external forces exist, as long as they are not too large. Momentum will therefore be conserved during collisions.

37. In an elastic collision, total kinetic energy is also conserved. In an inelastic collision, some kinetic energy is lost. In a completely inelastic collision, the two objects stick together after the collision. The center of mass of a system is the point at which external forces can be considered to act. Summary of Chapter 7, cont.