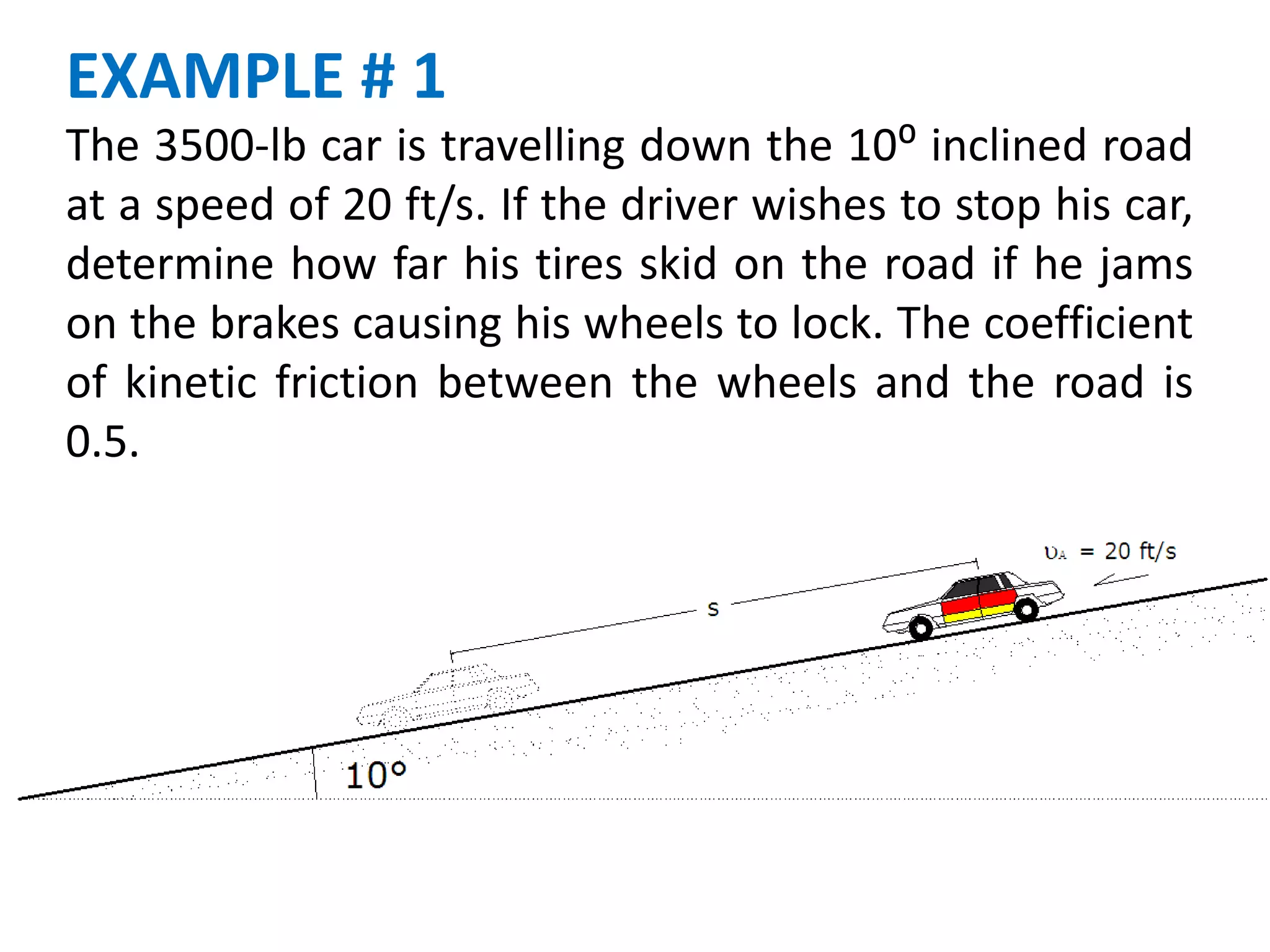
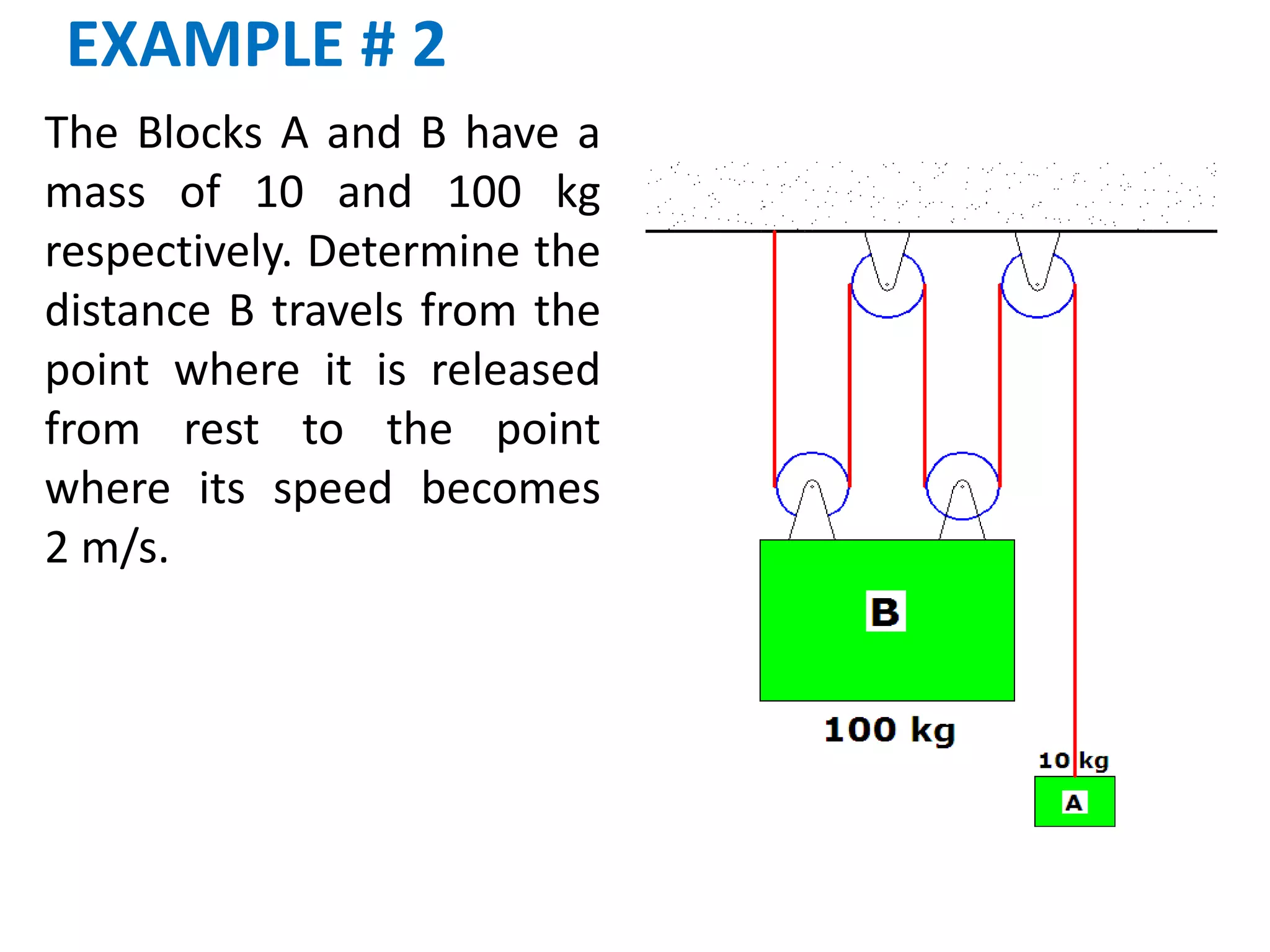
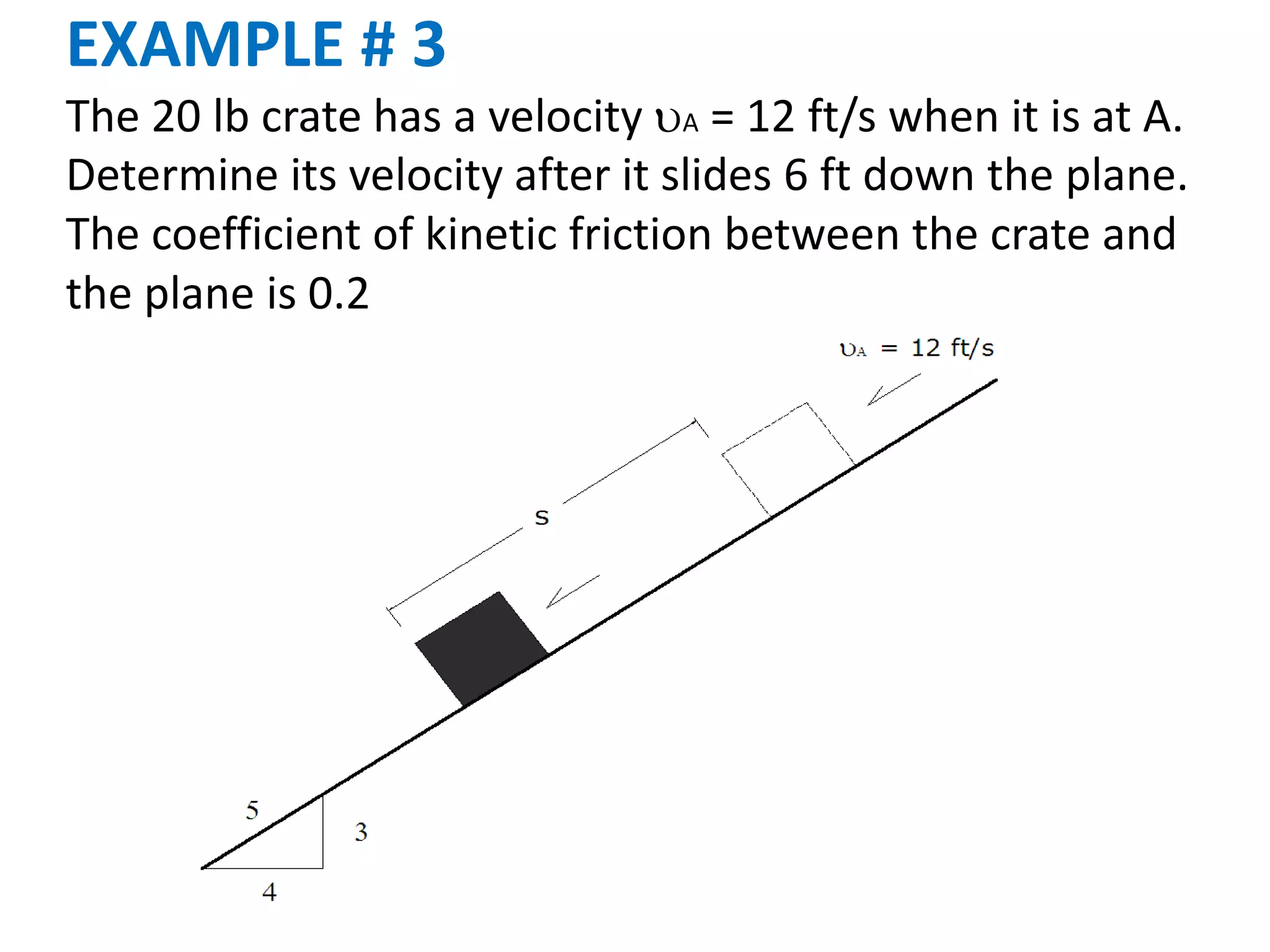
This document discusses work, energy, and their application to solving kinetics problems involving forces, velocities, and displacements. It defines work as the product of force and displacement. It also defines kinetic energy as the energy of motion and potential energy as energy due to position or gravitational interaction. The principle of work and energy states that the net work done on an object equals its change in kinetic energy. Examples are provided to demonstrate how to apply these concepts to calculate velocities, distances, tensions, and work in problems involving forces on moving objects.

1. M A R C H 1 2 , 2 0 1 4
KINETICS OF PARTICLES:
WORK and ENERGY

2. Integration of the Equations of motions
to obtain the Principle of Work and
Energy, principles that help to solve
problems involving Force, Velocity and
Displacement.
KINETICS OF PARTICLES:
WORK and ENERGY

3. Work of a Force
- Force exhibits Work when it undergoes a
displacement or it moves through some distance in
the direction of the Force.
Work done (U)
U = Force X displacement
U = F Cos   d
Vector Form
U = F  d

4. Work of a Force
If the Force is variable then the Total Work done is
U =  F  dS
Units: F = Newton (N = kg.m/s2)
U = Joule (J = N.m)
Note: -Moment of a force and the principle
of Work are in no way related.
-Moment is a Vector Quantity and
Work is a Scalar.

5. ENERGY
Energy of a Body is its capacity of doing Work.
It is equal to the work done in altering either
its motion or its velocity.
Kinetic Energy – energy possess by virtue of
its motion
Potential Energy – energy possess by virtue of
its gravitational interaction

6. KINETIC ENERGY
Kinetic Energy is measured in the amount of work
which a body can perform against some resistance
until it is brought to rest.
F = -F to bring the body to rest there must be
an opposing force
F = - ma a =  d/ds
F = - m   d/ds
F ds = - m  d integrate
 F ds = -  m  d Work done by a Force
KE = - 
0 m  d
KE = - m  2 d Kinetic Energy
KE = ½ m2

7. PRINCIPLE OF WORK and ENERGY
Equation of Particle:
F = ma F Cos  = mat
Since dr = ds along the path, then at =  d/ds, thus
F Cos  = m (  d/ds )
F Cos  ds = m  d integrate
Assume limits: s = s1 and  = 1 and s = s2 and  = 2
F Cos  ds = m  d
F Cos  ds = ½ m 2
2 - ½ m 1
2
U1-2 = ½ m 2
2 - ½ m 1
2

8. PRINCIPLE OF WORK and ENERGY
This equation represents the Principle of Work and Energy
U1-2 = ½ m 2
2 - ½ m 1
2
Whereas,
 U1-2 - sum of the work done by all the forces on the
particle as the particle moves from point 1 to
point 2
½ m 2
2 - ½ m 1
2- particle’s final and initial kinetic
energy are positive scalar quantity since they
do not depend on the direction of the velocity
KE = T = ½ m 2
U1-2 = T2 - T1
T1 + U1-2 = T2

9. The 3500-lb car is travelling down the 10⁰ inclined road
at a speed of 20 ft/s. If the driver wishes to stop his car,
determine how far his tires skid on the road if he jams
on the brakes causing his wheels to lock. The coefficient
of kinetic friction between the wheels and the road is
0.5.
EXAMPLE # 1

10. The Blocks A and B have a
mass of 10 and 100 kg
respectively. Determine the
distance B travels from the
point where it is released
from rest to the point
where its speed becomes
2 m/s.
EXAMPLE # 2

11. The 20 lb crate has a velocity A = 12 ft/s when it is at A.
Determine its velocity after it slides 6 ft down the plane.
The coefficient of kinetic friction between the crate and
the plane is 0.2
EXAMPLE # 3

12. A crate has a weight of 1500 lb. if it is pulled along the
ground at constant speed for a distance of 25 ft, and the
towing cable makes an angle of 15⁰ with the horizontal,
determine the tension in the cable and the work done
by the towing force. The coefficient of friction between
the ground and the crate is 0.55
EXAMPLE # 4